Constructing critical control parameters to keep vehicle away from divergent loss of stability

Figures & data

Figure 1. Two degrees of freedom bicycle model.

Figure 2. Graphical representation obtained using the Pevsner function $\overline{Y}=\overline{Y}({\delta }_2-{\delta }_1)$ for the geometrical analysis of a set of stationary states for the vehicle model described by Equations (1) and (2).

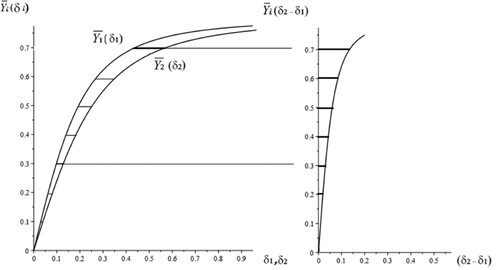
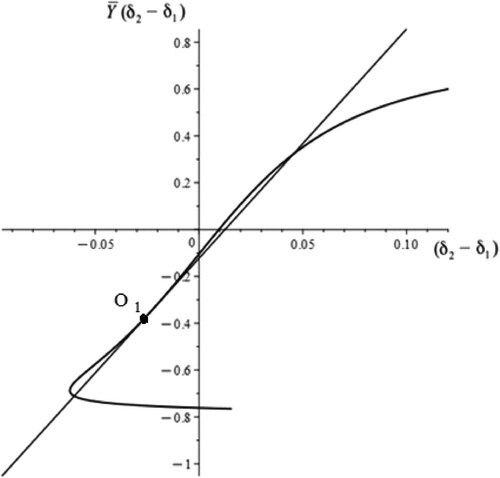
Figure 3. The points of intersection between a moving straight line and a fixed curve indicate a divergent loss of stability in the corresponding multiple stationary regime, i.e. a bifurcation of a fold.

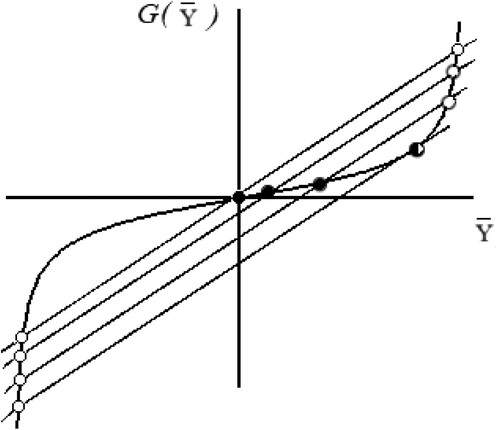
Figure 4. Bifurcation diagram (solid curve) defined by the Equations (23)-(24) and the (dash curve) obtained using the numerical continuation method.

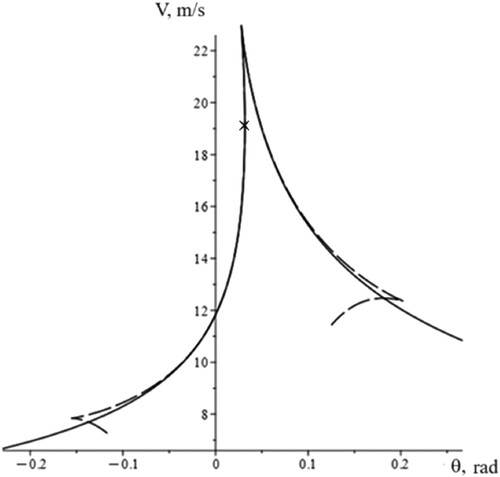
Figure 5. Steering Angle θ as function of time for the realisation of straight-line motion where $\theta (t)$ → ${\theta }_{(q)}=0.0315$rad.

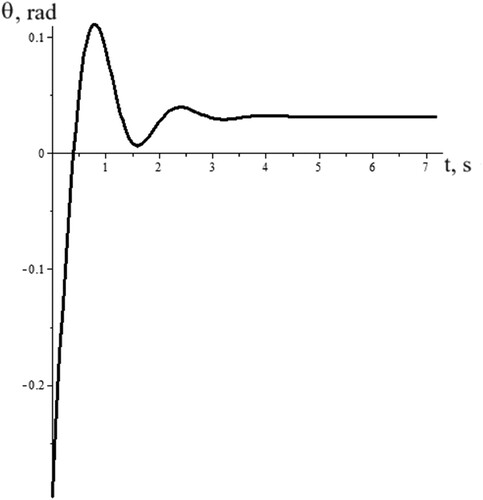
Figure 6. The stabilisation of straight-line motion generated by the steering angle $\theta (t)$ as solved by Equation (33).

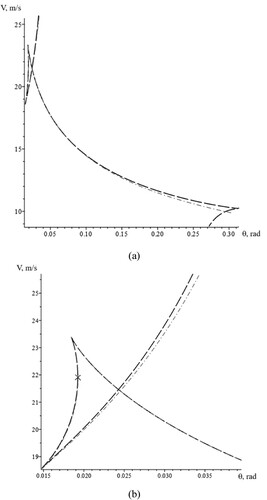
Figure 7. Analysis of divergent loss stability on the handling curve (with turning radius of R = 30 m); The long-dash curves are the handling curves and indicate the change in steering angle required for the vehicle to remain on a circlular trajectory of fixed radius if a change in the speed V occurs. The smooth solid curves are the bifurcation sets with the critical values of the control parameters (θ, V) corresponding to a divergent loss in stability for the stationary states of the system: (a) represents q =  μ = 0; (b) represents q =  0.3, μ = 0; (c) represents q =  0.3, μ = 0.03.

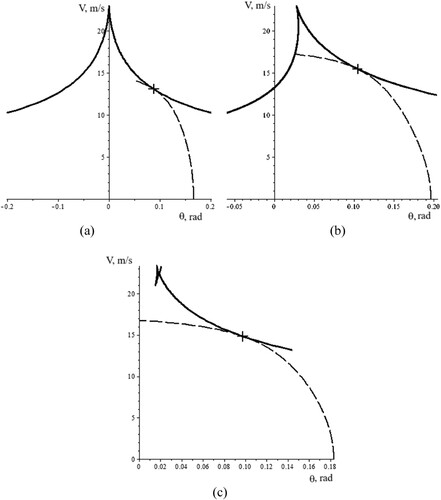
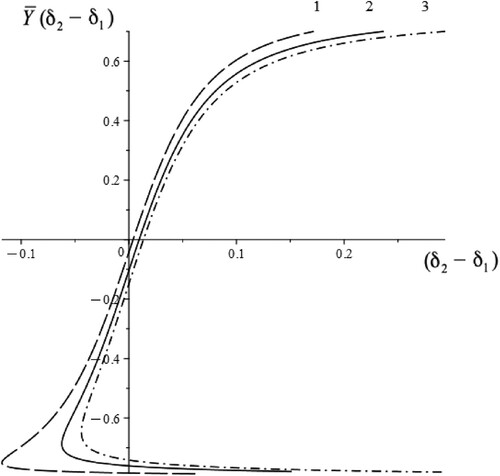
Figure 8. Graphical illustration of corrective steering angles under external lateral force; (a): the condition ${\overline{k}}_1>{\overline{k}}_2$, ${\kappa }_1={\kappa }_2$; (b): the condition ${\overline{k}}_1<{\overline{k}}_2$, ${\kappa }_1={\kappa }_2$; (c) and (d): ${\overline{k}}_1>{\overline{k}}_2$, ${\kappa }_1<{\kappa }_2$.

Figure 9. Graph of $\overline{Y}({\delta }_2-{\delta }_1,\mu )$ for different values of parameter μ $(1.{\mu }_1=0.01;2.{\mu }_2=0.0242;3.{\mu }_3=0.0342)$.

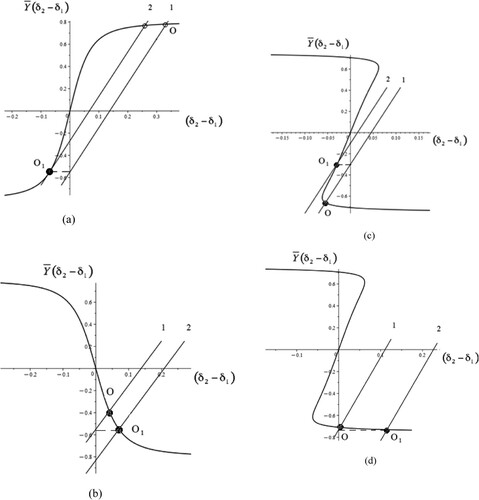
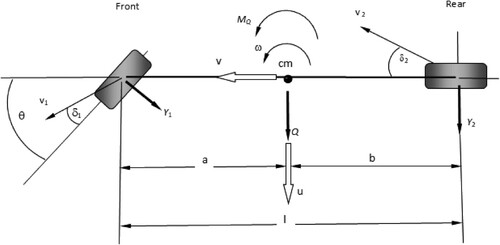
Figure 10. Determination of the corrective steering angle for straight-line motion with a moment of the external force acting about the centre of mass vehicle (μ = 0.0242, q = 0.3, v = 18 m/s).

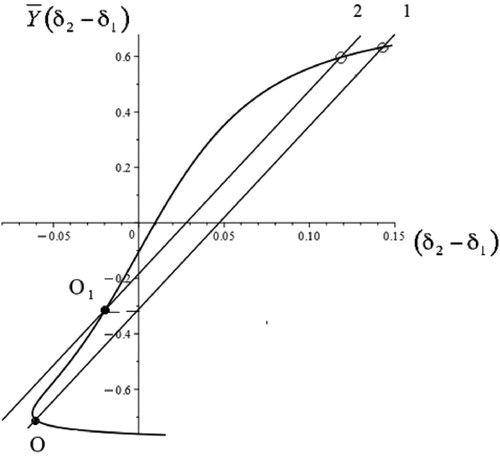
Figure 11. (a): Stability diagram with an additional moment of the external lateral forces acting about a vertical axis at the vehicle of mass centre (μ = 0.0242, q = 0.3); (b): Fragment of stability diagram with an additional moment of the external lateral forces acting about a vertical axis at the vehicle of mass centre (μ = 0.0242, q = 0.3).

Figure 12. The loss of divergent stability for straight-line vehicle motion (μ = 0.0242, q = 0.3) for critical values of the parameters ${{\theta }^{(1)}}_{(q,\mu )}=$0.01928rad, $V^{\times }=$21.91 m/s.