A fast and conformal heating scheme for producing large thermal lesions using a 2D ultrasound phased array

Figures & data

Figure 1. (a) Geometry of a 2D ultrasound phased array heating system. This 2D phased array was assumed to be mounted on a positioning system that can shift the array in the x and y directions. The target volume can be divided into several rectangular subregions and then heated sequentially; (b) four types of subregions are formed by using different numbers of scanned focal depths (in dashed regions). The former three were in 1 × 1 cm² of cross-sectional area with 1, 2, and 3 cm in length, respectively. The fourth case had 1.5 × 1.5 cm² of cross-sectional area with 3 cm in length.

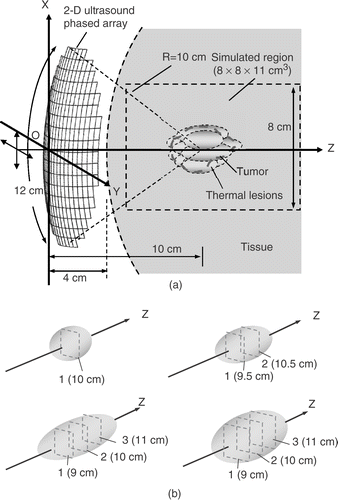
Figure 2. Focal point arrangement of each scanning plane with the scanning areas (a) 1 × 1 cm² and (b) 1.5 × 1.5 cm².

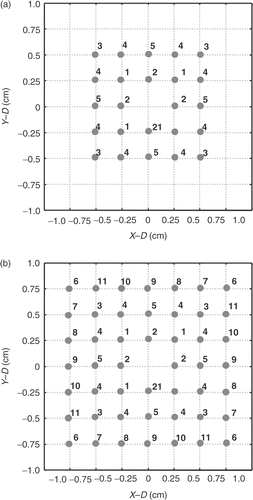
Figure 3. Simulated temperature profiles (using constant/thermal-dependent tissue parameters) compared with the experimental data of a 256-element 2D phased array system [14]. (a) and (b) spatial temperature distribution at the end of sonication (t = 20 s), (c) temperature response at the focal depth (z = 9 cm) and (d) at the pre-focal region (z = 6 cm).

Figure 4. Three-dimensional surface views of the formed thermal lesions (in TD = 60 and 240 min) to cover subvolumes of (a) 1 × 1 × 1 cm³, (b) 1 × 1 × 2 cm³, (c) 1 × 1 × 3 cm³, (d) 1.5 × 1.5 × 3 cm³ at 1 kg/m³/s of blood perfusion rate and (e) another 1.5 × 1.5 × 3 cm³ subvolume at 10 kg/m³/s.

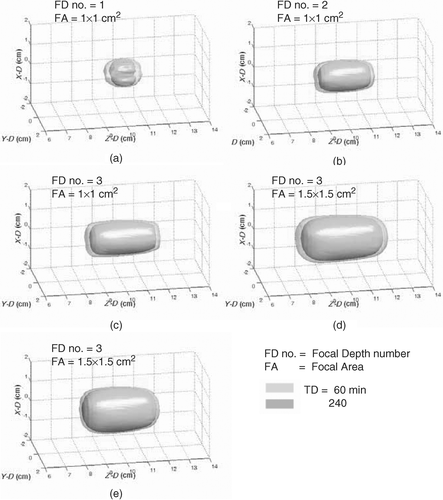
Figure 5. Two-dimensional TD contour distributions (TD = 60 and 240 min were shown) for Figure 4. Left columns show the X–Z plane (Y = 0 cm) distributions and the right columns show the X–Y plane (Z = 10 cm) distributions. Outer and inner contour for each subplot represent TD = 60 and 240 min, respectively.

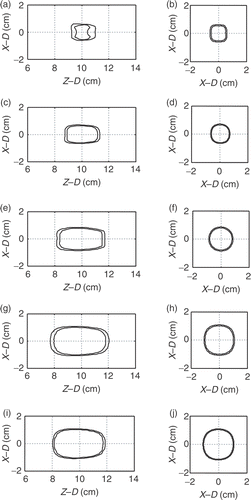
Table I.  Comparison of treatment results for different heating units and larger thermal lesions to conform a 3 × 3 × 3 cm³ PTV as well as an irregular PTV.

Case	PTV (cm^3)	Focal depth (cm)	Pattern no.	Subreg. no.	ton(s/min)	Tmax(°C)	TDmax (min)	CI240 (%)	EI240 (%)	EI60 (%)
1	1 × 1 × 1	12	5	–	40 s	65.6	2.9 × 10^5	–	–	–
2	1 × 1 × 2	11.5/12.5	10	–	45 s	68.7	4.3 × 10^6	–	–	–
3	1 × 1 × 3	11/12/13	15	–	70 s	71.2	8.4 × 10^7	–	–	–
4	1.5 × 1.5 × 3	11/12/13	33	–	170 s	73.8	4.0 × 10^8	–	–	–
5	1.5 × 1.5 × 3	11/12/13	33	–	250 s	80.6	6.5 × 10^10	–	–	–
6	3 × 3 × 3	–^1	–	9	44.5 min	78.7	2.3 × 10^10	100	49.8	71.0
7	3 × 3 × 3	–^1	–	9	33.8 min	74.3	6.1 × 10^8	100	34.3	55.3
8	3 × 3 × 3	–^2	–	4	28.1 min	77.2	7.5 × 10^9	100	60.3	76.4
9	3 × 3 × 3	–^2	–	4	31.5 min	86.7	1.2 × 10^13	100	57.1	63.3
10	Irregular 1^3	–^4	–	9	26.2 min	79.1	6.0 × 10^10	100	69.1	87.2
11	Irregular 2^5	–^4	–	4	14.4 min	73.1	2.9 × 10^8	100	33.8	70.1
12	Irregular 2^5	–^4	–	7	23.5 min	72.4	1.7 × 10^8	100	96.2	136.7

¹Power setting in case 3 is used to sequentially heat nine 1 × 1 × 3 cm³ subregions; ²Power setting in case 4 is used to sequentially heat four 1.5 × 1.5 × 3 cm³ subregions; ³See Figure 6; ⁴Power setting in case 1, 2, and 3 are used alternatively to sequentially heat various lengths of subvolumes to form irregular volume; ⁵See Figure 8. (PTV = Planning target volume, t_on = heating time, t_max = maximal temperature, TD_max = maximal TD, CI₂₄₀ = coverage index using TD = 240 min as threshold, EI₆₀ and EI₂₄₀ = external volume index using TD = 60 or 240 min as thresholds, respectively). Cases 1–4 show the results of single exposure under the reference blood perfusion rate (1 kg/m³/s; case 5 shows a high blood perfusion case (10 kg/m³/s) compared with case 4; case 6, 7, and 8 show the results of treating a large cubic volumes (3 × 3 × 3 cm³) by dividing into 9 and 4 subregions, respectively, under the reference blood perfusion rate (1 kg/m³/s); case 9 show a high blood perfusion case (10 kg/m³/s) compared with case 8; case 10 is a irregular target volume treatment, and cases 11 and 12 are results of a irregular real tumor treatment.

Figure 6. Three-dimensional surface views of the formed thermal lesions (in TD = 60 and 240 min) in: (a) and (b) two different heating sequences to conform a 3 × 3 × 3 cm³ cubic volume by sequentially heating nine 1 × 1 × 3 cm³ subvolumes at 1 kg/m³/s of blood perfusion rate; (c) and (d) conforming a 3 × 3 × 3 cm³ cubic volume by sequentially heating four 1.5 × 1.5 × 3 cm³ subvolumes at 1 and 10 kg/m³/s of blood perfusion rates, respectively; (e) conforming an irregular volumes by sequentially heating 1 × 1 × 1, 1 × 1 × 2, and 1 × 1 × 3 cm³ subvolumes. The numbers were denoted as the sequence of each subvolume heating, and a 3D cartoon object located at upper-right corner of each subplot represents the shapes and heating unit divisions to the entire target volume.

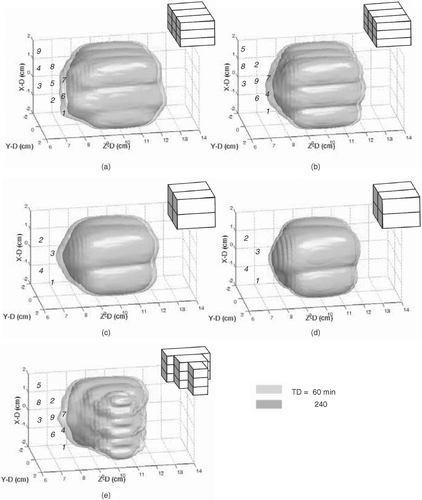
Figure 7. Two-dimensional TD contour distributions (TD = 60 and 240 min were shown) for Figure 6. Left columns show the X–Z plane (Y = 0 cm) distributions and the right columns show the X–Y plane (Z = 10 cm) distributions. Rectangular regions drawn in dashed lines represent the target volume regions appeared in individual subplots. Outer and inner contour for each subplot represent TD = 60 and 240 min, respectively.

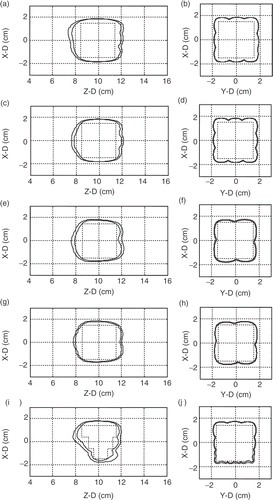
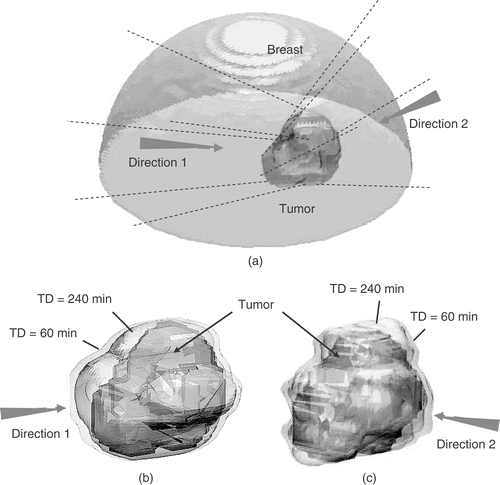
Figure 8. One practical treatment case of an irregular tumor located in female breast: (a) geometrical relation between breast and tumor; (b) and (c) surface views of PTV (pointed out by arrows) and TD = 60 and 240 min iso-surfaces (pointed out by lines) after treatment while using two different power incident directions. Arrows indicate the incident direction of the ultrasonic energy.

Daum DR, Hynynen K. A 256-element ultrasonic phased array system for the treatment of larger volumes of deep seated tissue. IEEE Trans Ultrason Ferroelec Freq Contr 1999; 46: 1254–1268

 PubMed Web of Science ®Google Scholar