The role of direct capital cash transfers towards poverty and extreme poverty alleviation - an omega risk process

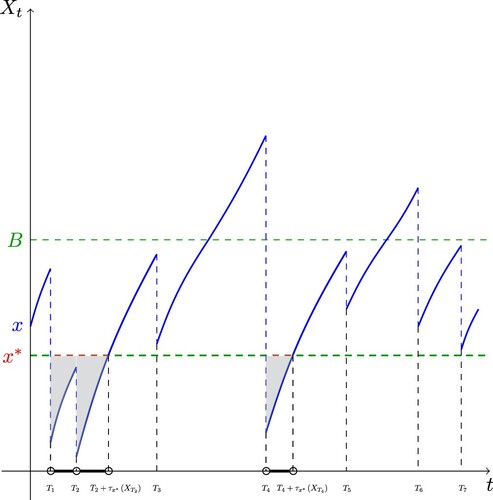
Figures & data

Figure 1. (a) Consumption and savings (b) Trajectory of the stochastic process $X_t$.

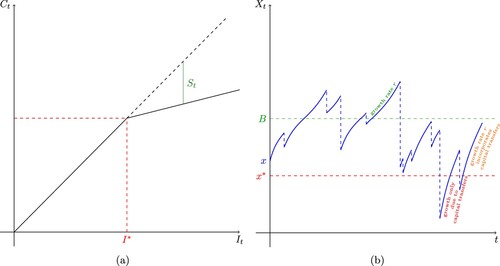
Figure 2. (a) Trapping probability ${\psi }^P\left(x\right)$ when $Z_i\sim \mathrm{Beta}(0.8,1)$, a = 0.1, b = 4, $c_S=0.4$, B = 2, $\lambda =1$ and $x^{\ast }=1$ for $c_T=0.1,1,10,100$ (b) Trapping probability ${\psi }^P\left(x\right)$ when $Z_i\sim \mathrm{Beta}(0.8,1)$, a = 0.1, $b=4$, $c_S=0.4$, $c_T=0.25$, $\lambda =1$ and $x^{\ast }=1$ for B = 1, 2, 3, 4.

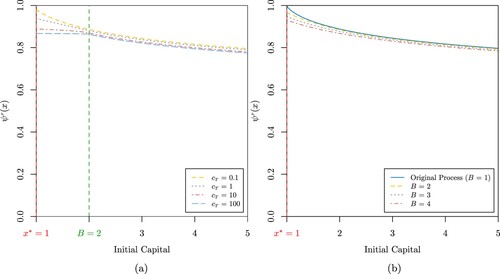
Figure 3. (a) Probability of extreme poverty ${\psi }^{\mathrm{EP}}\left(x\right)$ when $Z_i\sim \mathrm{Beta}(0.8,1)$, a = 0.1, b = 4, $c_S=0.4$, B = 2, $\lambda =1$, $x^{\ast }=1$ and ${\omega }_1\left(x\right)=0.02$ for $c_T=0.25,0.5,0.75,1$ (b) Probability of extreme poverty ${\psi }^{\mathrm{EP}}\left(x\right)$ when $Z_i\sim \mathrm{Beta}(0.8,1)$, a = 0.1, b = 4, $c_S=0.4$, $c_T=0.25$, $\lambda =1$, $x^{\ast }=1$ and ${\omega }_1\left(x\right)=0.02$ for $B\to x^{\ast +}$ and $B=2,3,4$.

Figure 4. Probability of extreme poverty ${\psi }^{\mathrm{EP}}\left(x\right)$ when $Z_i\sim \mathrm{Beta}(0.8,1)$, a = 0.1, b = 4, $c_S=0.4$, $c_T=0.25$, B = 2, $\lambda =1$, $x^{\ast }=1$ and ${\omega }_1\left(x\right)={\omega }_c$ for ${\omega }_c=0.02,0.05,0.09$.

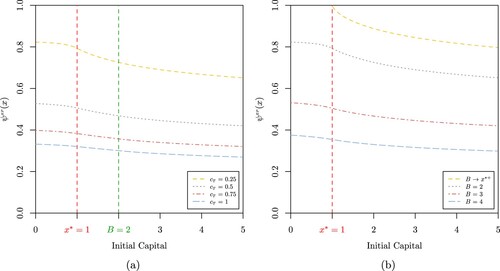
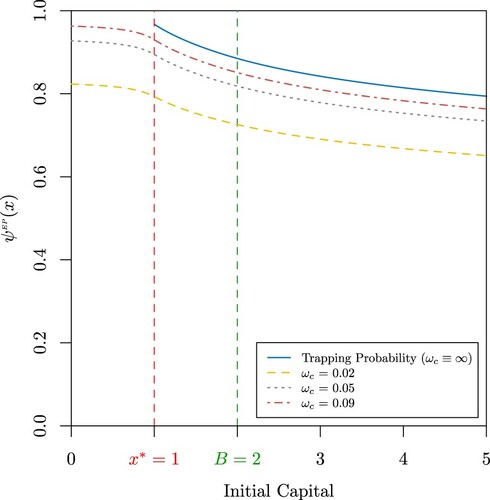
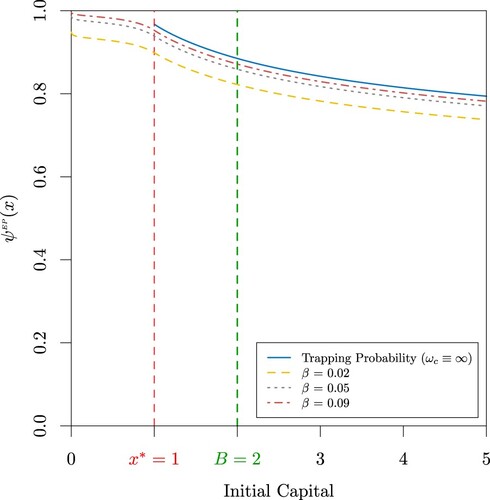
Figure 5. (a) Probability of extreme poverty ${\psi }^{\mathrm{EP}}\left(x\right)$ when $Z_i\sim \mathrm{Beta}(0.8,1)$, a = 0.1, b = 4, $c_S=0.4$, B = 2, $\lambda =1$, $x^{\ast }=1$ and ${\omega }_2\left(x\right)=\frac{0.02}{x}$ for $c_T=0.25,0.5,0.75,1$ (b) Probability of extreme poverty ${\psi }^{\mathrm{EP}}\left(x\right)$ when $Z_i\sim \mathrm{Beta}(0.8,1)$, a = 0.1, b = 4, $c_S=0.4$, $c_T=0.25$, $\lambda =1$, $x^{\ast }=1$ and ${\omega }_2\left(x\right)=\frac{0.02}{x}$ for $B\to x^{\ast +}$ and $B=2,3,4$.

Figure 6. Probability of extreme poverty ${\psi }^{\mathrm{EP}}\left(x\right)$ when $Z_i\sim \mathrm{Beta}(0.8,1)$, a = 0.1, b = 4, $c_S=0.4$, $c_T=0.25$, B = 2, $\lambda =1$, $x^{\ast }=1$ and ${\omega }_2\left(x\right)=\frac{\text{β}}{x}$ for $\text{β}=0.02,0.05,0.09$.

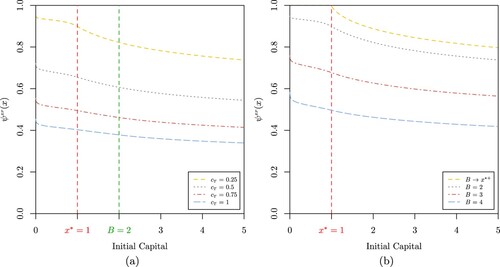
Figure 7. (a) Cash transfer rate $c_T$ and capital barrier level B required to attain a given target trapping probability of ${\psi }^P\left(x\right)=0.01$ when $Z_i\sim \mathrm{Beta}(1.25,1)$, a = 0.1, b = 4, $c_S=0.4$, $\lambda =1$ and $x^{\ast }=1$ for initial capital $x=1.5,2,3,4$ (b) Cash transfer rate $c_T$ and capital barrier level B required to attain a given target probability of extreme poverty of ${\psi }^{\mathrm{EP}}\left(x\right)=0.01$ when $Z_i\sim \mathrm{Beta}(1.25,1)$, $a=0.1$, b = 4, $c_S=0.4$, $\lambda =1$, $x^{\ast }=1$ and ${\omega }_c=0.09$ for initial capital $x=1.5,2,3,4$.

Figure 8. Computation of ${\mathrm{\Psi }}^{\mathrm{EP}}(\omega ,x)$ conditional on a realised sample path.

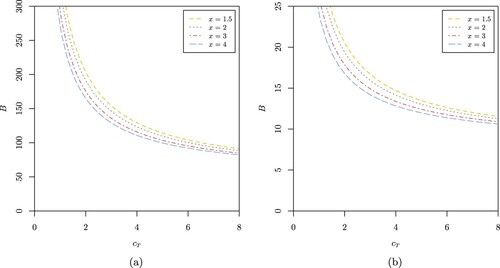
Figure 9. (a) Probability of extreme poverty ${\hat{\psi }}^{\mathrm{EP}}(x{)}_n$ when n = 10, 000, $Z_i\sim \mathrm{Beta}(0.8,1)$, a = 0.1, b = 4, $c_S=0.4$, B = 2, $\lambda =1$, $x^{\ast }=1$ and ${\omega }_1\left(x\right)=0.02$ for $c_T=0.25,0.5,0.75,1$ (b) Probability of extreme poverty ${\psi }^{\mathrm{EP}}(x{)}_n$ when n = 10, 000, $Z_i\sim \mathrm{Beta}(0.8,1)$, a = 0.1, b = 4, $c_S=0.4$, $c_T=0.25$, $\lambda =1$, $x^{\ast }=1$ and ${\omega }_1\left(x\right)=0.02$ for $B\to x^{\ast +}$ and $B=2,3,4$.

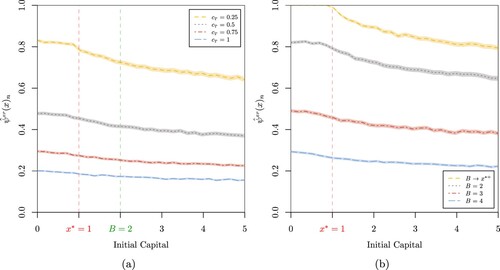
Figure 10. Probability of extreme poverty ${\hat{\psi }}^{\mathrm{EP}}(x{)}_n$ when n = 10, 000, $Z_i\sim \mathrm{Beta}(0.8,1)$, a = 0.1, b = 4, $c_S=0.4$, $c_T=0.25$, B = 2, $\lambda =1$, $x^{\ast }=1$ and ${\omega }_1\left(x\right)={\omega }_c$ for ${\omega }_c=0.02,0.05,0.09$.

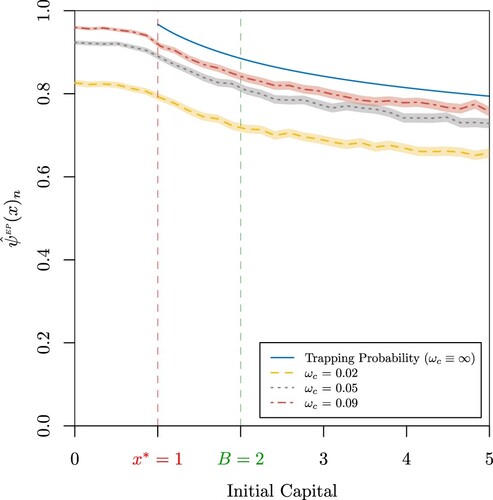
Figure 11. (a) Probability of extreme poverty ${\hat{\psi }}^{\mathrm{EP}}(x{)}_n$ when n = 10, 000, $Z_i\sim \mathrm{Beta}(0.8,1)$, a = 0.1, b = 4, $c_S=0.4$, B = 2, $\lambda =1$, $x^{\ast }=1$ and ${\omega }_2\left(x\right)=\frac{0.02}{x}$ for $c_T=0.25,0.5,0.75,1$ (b) Probability of extreme poverty ${\psi }^{\mathrm{EP}}\left(x\right)$ when $Z_i\sim \mathrm{Beta}(0.8,1)$, a = 0.1, b = 4, $c_S=0.4$, $c_T=0.25$, $\lambda =1$, $x^{\ast }=1$ and ${\omega }_2\left(x\right)=\frac{0.02}{x}$ for $B\to x^{\ast +}$ and $B=2,3,4$.

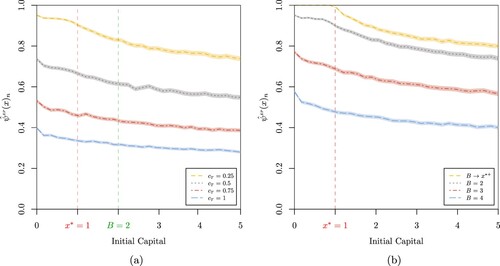
Figure 12. Probability of extreme poverty ${\hat{\psi }}^{\mathrm{EP}}(x{)}_n$ when n = 10, 000, $Z_i\sim \mathrm{Beta}(0.8,1)$, a = 0.1, b = 4, $c_S=0.4$, $c_T=0.25$, B = 2, $\lambda =1$, $x^{\ast }=1$ and ${\omega }_2\left(x\right)=\frac{\text{β}}{x}$ for $\text{β}=0.02,0.05,0.09$.

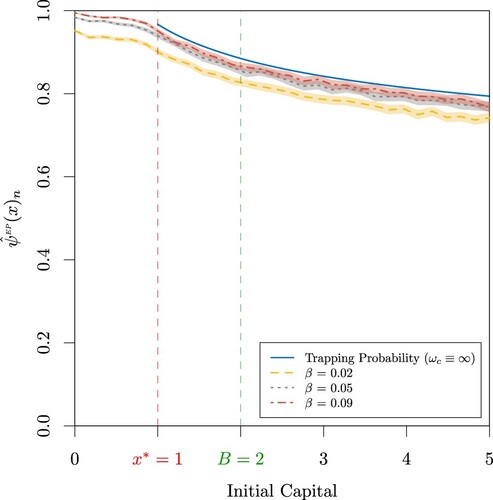
Figure A1. Effects of the rate of consumption $(0<a<1)$, income generation $(b>0)$, investment or savings $(0<c_S<1)$, the parameter of the Beta distribution $(\alpha >0)$ (i.e. expected remaining proportion of capital), the expected capital loss frequency $(\lambda >0)$, the critical capital $(x\ge x^{\ast })$, the capital barrier level $(B>x^{\ast })$ and the capital transfer rate $(c_T>0)$ on the trapping probability of the original model obtained in Henshaw et al. (2023) (in red) and on the trapping probability of the model with capital cash transfers (in blue) for initial capital $x=1.3\left(\mathrm{solid}\right),1.7\left(\mathrm{dashed}\right),4.0\left(\mathrm{dotted}\right),6.0(\mathrm{dashed}-\mathrm{dotted})$.

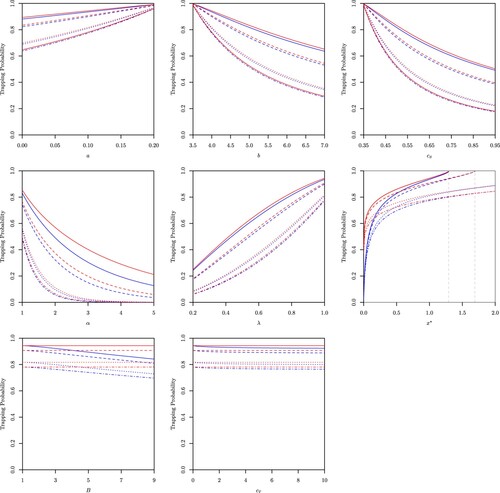
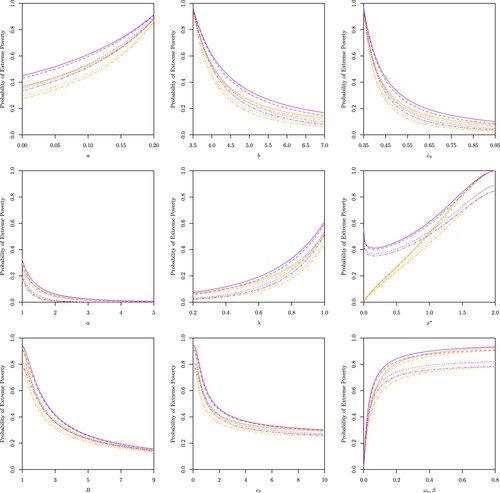
Figure A2. Effects of the rate of consumption $(0<a<1)$, income generation $(b>0)$, investment or savings $(0<c_S<1)$, the parameter of the Beta distribution $(\alpha >0)$ (i.e. expected remaining proportion of capital), the expected capital loss frequency $(\lambda >0)$, the critical capital $(x\ge x^{\ast })$, the capital barrier level $(B>x^{\ast })$, the capital transfer rate $(c_T>0)$ and the extreme poverty rate function on the probability of extreme poverty for a constant extreme poverty rate function (in orange) and an exponential extreme poverty rate function (in purple) for initial capital $x=1.3\left(\mathrm{solid}\right),1.7\left(\mathrm{dashed}\right),4.0\left(\mathrm{dotted}\right),6.0(\mathrm{dashed}-\mathrm{dotted})$.

Henshaw K., Ramirez J. M., Flores-Contró J. M., Thomann E. A., Loke S. H. & Constantinescu C. D. (2023). On the impact of insurance on households susceptible to random proportional losses: an analysis of poverty trapping. Working Paper.

 Google Scholar