Combinatorics of Correlated Equilibria

Figures & data

Fig. 1 The correlated equilibrium polytope of the Traffic Lights example is a bipyramid where three of its vertices are Nash equilibria. Its f-vector is $(1,5,9,6,1)$ and its face lattice can be seen on the right.

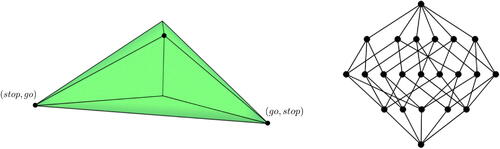
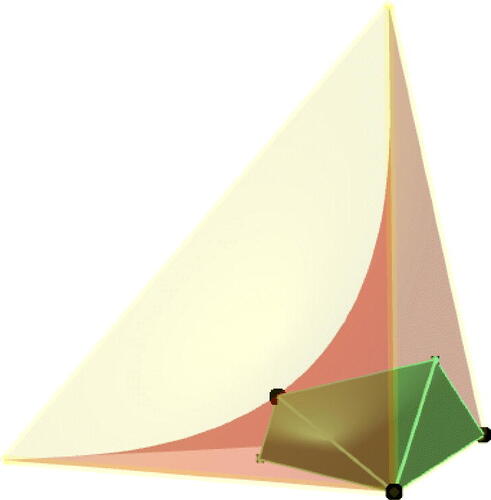
Fig. 3 A 3-dimensional correlated equilibrium polytope (green) inside the probability simplex ${\Delta }_3$ (yellow) for a $(2\times 2)$-game. Its Nash equilibria (black) are the intersection with the Segre variety (red). This picture applies to the Traffic Lights example (Examples 2.1, 2.3, 2.6) as well as the Hawk-Dove game (Example 5.1).

Table

		Player 2
		go	stop
Player 1	go	$(-99,-99)$	(1, 0)
	stop	(0, 1)	0, 0

Fig. 2 The vertices of the correlated equilibrium polytope for the Traffic Lights example (Example 2.3).

Table

		Player 2
		Hawk	Dove
Player 1	Hawk	$\left(\frac{V-C}{2},\frac{V-C}{2}\right)$	$(V,0)$
	Dove	$(0,V)$	$\left(\frac{V}{2},\frac{V}{2}\right)$

Fig. 4 The graph of the combinatorially unique 5-dimensional polytope that arises as the correlated equilibrium polytope of a $(2\times 3)$-game, as described in Theorem 5.9.

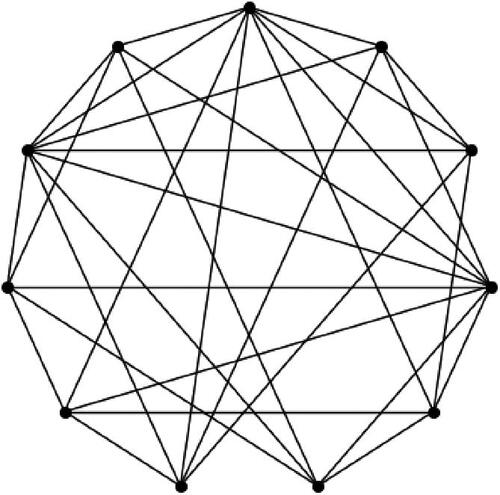
Table 1 The number of unique combinatorial types of P_G of each dimension for a $(2\times n)$-game in a random sampling of size $100000$.

Unique combinatorial types by dimension
Dimension	0	3	5	7	9
$(2\times 2)$	1	1	0	0	0
$(2\times 3)$	1	1	1	0	0
$(2\times 4)$	1	1	1	3	0
$(2\times 5)$	1	1	1	3	4