Kronecker Sequences with Many Distances

Figures & data

Fig. 1 The best current upper and lower bounds for the maximum number of distances in the Euclidean norm (${\overline{g}}_2^d$, purple) and the maximum norm (${\overline{g}}_{\infty }^d$, green) as a function of the dimension.

Fig. 2 Left: plot of $g^1(\alpha ,5)$. Right: the Kronecker sequence for $\alpha =0.28$, showing three shortest distances, $d(\alpha ,5\alpha )<d(2\alpha ,5\alpha )<d(2\alpha ,3\alpha )$.

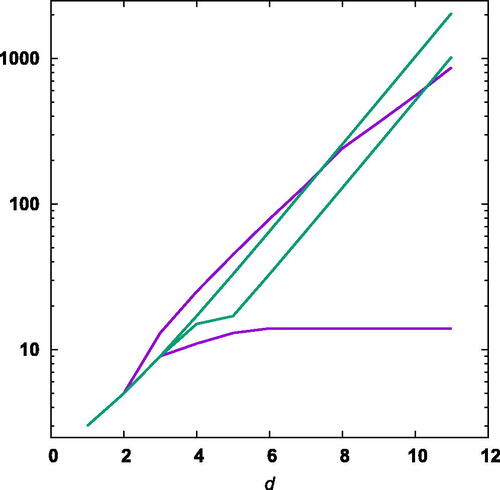
Fig. 3 Upper left: plot of $g_2^2(\alpha ,9)$ in the α plane. The color (black for 1 to yellow for 5) indicates $g_2^2(\alpha ,9)$, that is, the number of distinct shortest distances for N = 9, the given α and Euclidean metric. The region with five distances is too small to be visible and shown in the upper right panel. Lower left and right: Plots of $g_{\infty }^2(\alpha ,11)$ in the α plane, that is, for N = 11 and the maximum metric.

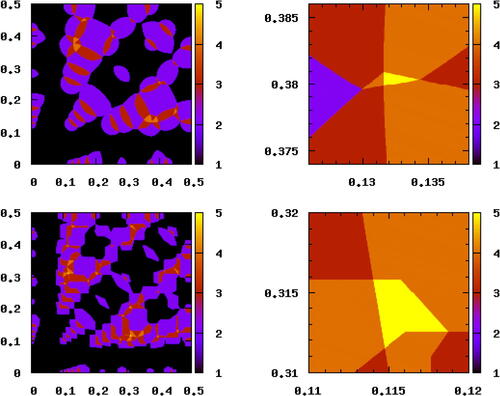
Fig. 4 Upper left: the Kronecker sequence for $\alpha =(0.132,0.38)$, showing five shortest distances in the Euclidean metric, $d_2(\alpha ,9\alpha )<d_2(2\alpha ,9\alpha )<d_2(3\alpha ,9\alpha )<d_2(4\alpha ,9\alpha )<d_2(5\alpha ,7\alpha )$. Upper right: Formation of the curved triangle and other structure in the upper right panel of Figure 3. Here, the two components of α are plotted, with $C_{m,n}$ the circular arc defined by $\mathit{\text{⏧mα⏧}}=\mathit{\text{⏧nα⏧}}$ in the Euclidean metric. Lower left: Kronecker sequence for $\alpha =(0.115,0.314)$ showing the five shortest distances in the maximum metric, $d_{\infty }(\alpha ,11\alpha )<d_{\infty }(2\alpha ,11\alpha )<d_{\infty }(4\alpha ,11\alpha )<d_{\infty }(5\alpha ,11\alpha )<d_{\infty }(6\alpha ,5\alpha )$. Lower right: Formation of the pentagon in the lower right panel of Figure 3. For $N_{n,j}$, see equation (9)(9) $$\mathit{⏧n\alpha }{⏧}_p=\{\begin{array}{cc}{\left(\sum _{j=1}^d{N}_{n,j}^p\right)}^{1/p}& p<\infty \\ {\mathrm{\text{max}}}_{1\le j\le d}{N}_{n,j}& p=\infty \end{array}$$(9) . The boundary of the pentagonal solution set consists of line segments where various combinations of these are equal.

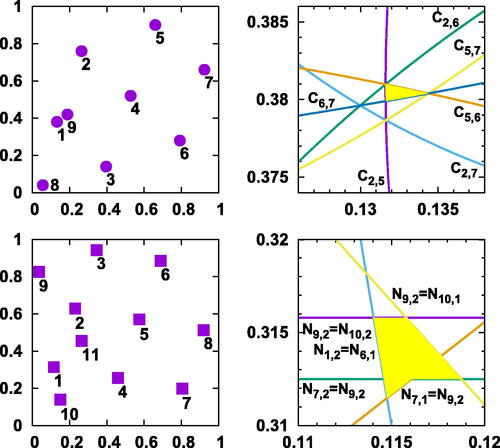
Table 1 Examples where the bound equation (15(15) $$N\ge 2g_p^d-1.$$(15) ) is tight for the Euclidean norm.

$g_2^d(\alpha ,N)$	N	α
2	3	1/2
3	5	3/11
4	7	(5, 8)/24
5	9	(15,43)/113
6	11	(24,69,111)/232
7	13	(9,24,29,42)/89
8	15	(12,14,35,57,76)/158

Table 2 Examples where the bound equation (15(15) $$N\ge 2g_p^d-1.$$(15) ) is tight for the maximum norm.

$g_{\infty }^d(\alpha ,N)$	N	α
2	3	1/2
3	5	3/11
4	7	(6, 16)/35
5	9	(5, 10, 17)/36
6	11	(12,35,57)/118
7	13	(9,21,34,39)/80
8	15	(7,23,35,47)/96
9	17	(9,33,52,67)/136
10	19	(11,25,31,47,95)/192
11	21	(13,27,34,55,111)/224
12	23	(15,39,63,95,127)/256
13	25	(19,31,41,79,159)/320
14	27	(41,61,79,89,159)/320

Table 3 Examples with $g_p^3(\alpha ,N)=9$.

p	N	α
1	148	(0.16915,0.1769,0.2109)
1.3	148	(0.16903,0.177,0.2109)
1.2	124	(0.009,0.06564,0.366233)
2	124	(0.0092,0.06572,0.3662)
1.9	58	(0.02035,0.0727,0.38535)
3	58	(0.0201,0.0728,0.3853)
2.5	94	(0.01217,0.35409,0.409912)
$\infty$	94	(0.0118,0.35395,0.41)

Interpolating these solutions covers all p-norms.