Too many zeros and/or highly skewed? A tutorial on modelling health behaviour as count data with Poisson and negative binomial regression

Figures & data

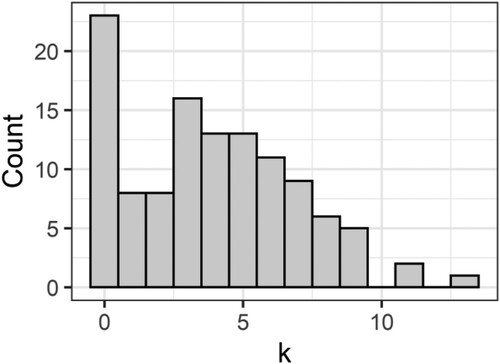
Figure 1. Histograms of real count data. Left panel is the number of views on YouTube of videos about scoliosis (Staunton et al., 2015). Right panel is the number of days on which participants sought help from a health professional over 30 days (Anwar et al., 2017).

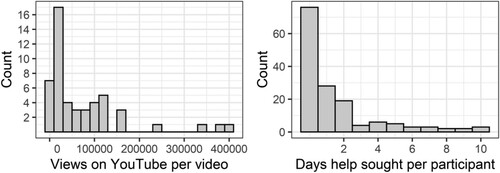
Figure 2. Left panel shows the shape of the Poisson distribution (number of events on the x-axis; probability of observing that number of events on the y-axis) for various values of λ. Right panel shows the shape of the negative binomial distribution for various values of μ and θ.

Figure 3. Hypothetical data with a clear bi-modal distribution, with the first peak at zero.

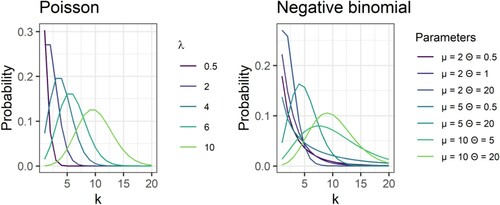
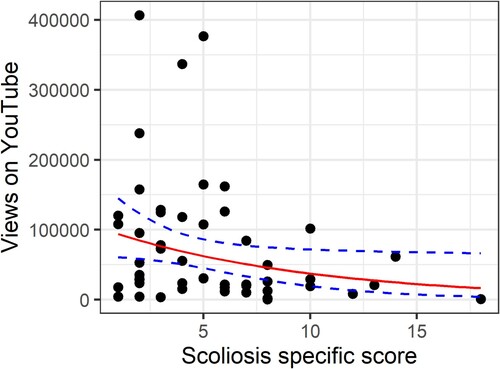
Figure 4. Scoliosis-specific score against number of YouTube views controlling for age. Original data in black, data simulated with a Poisson model in red. Upper and lower ellipses highlight original data points outside the simulated range. Note that Figures from the sim.plot function automatically ‘jitter’ data points a little bit so that points that might otherwise be on top of each other are slightly offset.

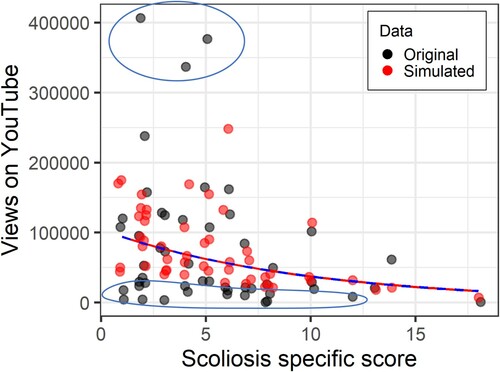
Figure 5. Two example rootograms from the countreg package. The left shows a model fit with a Poisson, and the right, a hurdle negative binomial model. Purple arrows on the left highlight a substantial underprediction of zeros in the Poisson, and then a ‘run’ of over-predictions at one through five. In contrast, the hurdle negative binomial accurately predicts the right number of zeros, and there are only a number of minor deviations (purple arrows), but they are not consecutive.

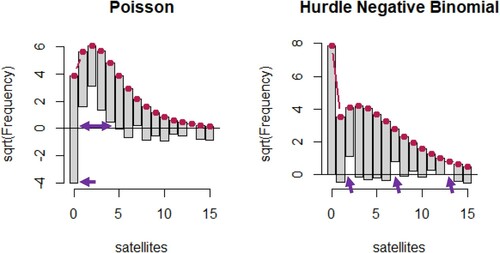
Table 1. Availability of different analyses for count data in different software packages.

	R	SPSS	Jamovi
Poisson	glm(family = ‘poisson’)	Generalised Linear Models (Type of Model = Poisson loglinear)	Yes
Quasi-Poisson	glm(family = ‘quasi-poisson’)	Yes^a	Yes
Negative binomial	glm.nb	Generalised Linear Models (Type of Model = Custom^b)	Yes
Quasi-binomial	glm(family = ‘quasi-binomial’)	No	No
Plot-based diagnostics	Yes	No	No
Zero-inflated Models	zeroinfl (dist = ‘poisson’/'negbin')	No^c	No
Hurdle Models	hurdle(dist = 'poisson'/‘negbin’)	No	No

^a You can achieve something similar by changing the ‘Scale Parameter Method’ from 1 (i.e. mean and variance are constrained to being the same) to (Pearson chi-square).

^b Do not select ‘Negative binomial with log link’(!).

^c Technically you can, but by using R within SPSS, after installing R and integrating it with SPSS. I have done this previously, and found it to be probably more difficult than familiarising yourself with R. Since then R has become easier to use, including an ability to seamlessly read in SPSS data with the haven package (Wickham & Miller, 2020).

Figure 6. Scoliosis-specific score against number of YouTube views controlling for age. Original data in black, data simulated with a linear model in red. Ellipses highlight where the simulated data does not overlap with the original data.

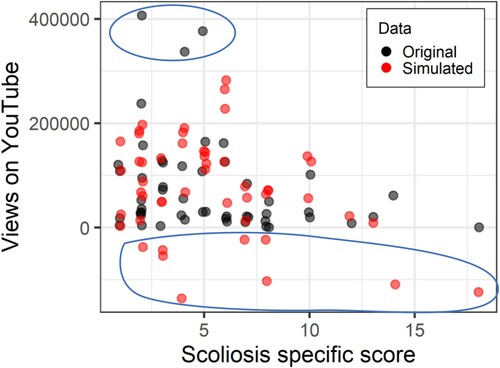
Figure 7. Scoliosis-specific score against number of YouTube views controlling for age. Original data in black, data simulated with a Poisson model in red.

Figure 8. Fit curve for quasi-Poisson (estimated fit in red, 95% CI in blue).

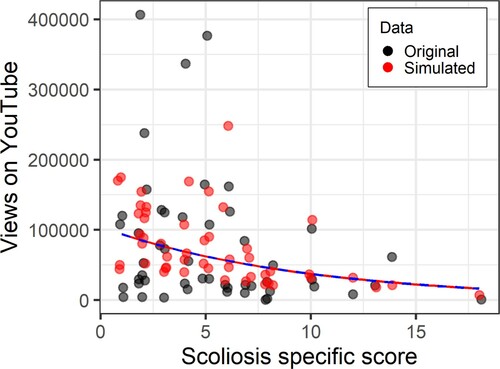
Figure 9. Scoliosis-specific score against number of YouTube views controlling for age. Original data in black, data simulated with a negative binomial model in red. The top-left panel has the random seed set to 45. The subsequent three panels are re-running the same function immediately afterwards, and demonstrates the importance of running multiple simulations.

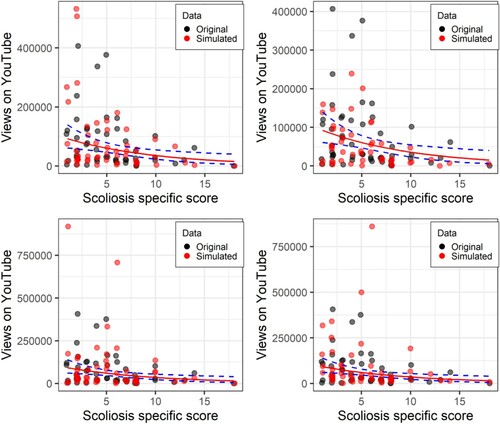
Table 2. Regression coefficients and model fit for different distribution models.

	Standard linear regression	Poisson regression	Quasi-Poisson regression	Negative binomial regression
Intercept	−85051.90	9.22	9.22	8.79
Standard error	57755.15	0.003	0.692	0.656
p value	0.147	<0.001	<0.001	<0.001
Age of video	77.58	0.000977	0.000977	0.00115
Standard error	21.21	<0.001	0.0002	0.037
p value	<0.001	<0.001	<0.001	<0.001
Scoliosis score	−4428.20	−0.102	−0.102	−0.106
Standard error	3185.31	0.001	0.049	0.0002
p value	0.171	<0.001	0.045	0.004
AIC	[not comparable]	2761005	NA	1205

Note: Coefficients for linear regression are in number of views. For the count distribution, they are natural logs of the number of views.

Figure 10. Number of days on which participants reported symptoms as a predictor of days on which participants visited a healthcare professional. Original data in black, Data simulated from a linear model in red.

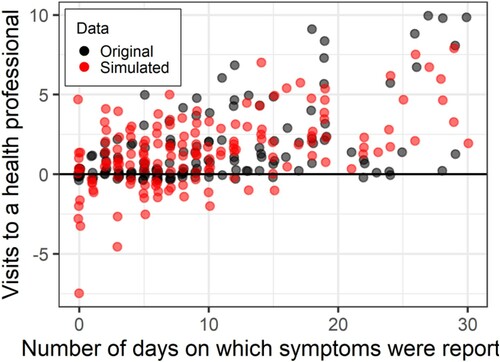
Figure 11. Simulated versus original data with Poisson fit on a scatterplot (left) and rootogram (right). Circle size is used to illustrate the number of overplotted points.

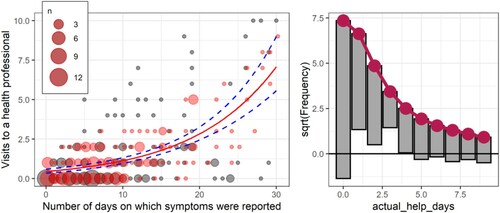
Figure 12. Simulated versus original data with negative binomial fit on a scatterplot (left) and rootogram (right).

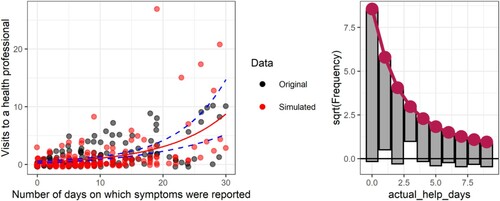
Figure 13. Rootograms for various count models for the number of days on which a health professional was visited.

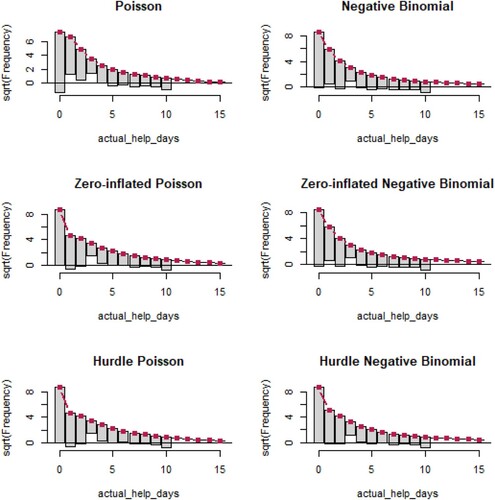
Table 3. Regression coefficients and model fit for different distribution models.

	Poisson regression	Negative binomial regression	Zero-inflated Poisson	Zero-inflated negative binomial	Hurdle Poisson	Hurdle negative binomial
Intercept	−1.17	−1.18	0.13	−1.01	0.16	−0.04
Std. error	0.35	0.54	0.39	0.50	0.40	0.59
p value	<0.001	0.03	0.7	0.046	0.7	0.9
Symptom days	0.092	0.104	0.069	0.107	0.067	0.077
Std. Error	0.007	0.014	0.009	0.014	0.009	0.015
p value	<0.001	<0.001	<0.001	0.017	<0.001	<0.001
Impulsivity	−.012	−.014	−0.015	−0.017	−0.015	−0.019
Std. Error	0.004	0.007	0.004	0.006	0.005	0.007
p value	0.006	0.053	<0.001	0.009	<0.001	0.004
AIC	514	458	467	454	467	459

Notes: Estimates are omitted for the zero-inflated and hurdle step of the model for simplicity. These are included in the tutorial files.

Staunton, P. F., Baker, J. F., Green, J., & Devitt, A. (2015). Online curves: A quality analysis of scoliosis videos on YouTube. Spine, 40(23), 1857–1861. doi:https://doi.org/10.1097/BRS.0000000000001137

 PubMed Web of Science ®Google Scholar

Anwar, M., Green, J. A., Norris, P., & Bukhari, N. I. (2017). Prospective daily diary study reporting of any and all symptoms in healthy adults in Pakistan: Prevalence and response. BMJ Open, 7(11), e014998. doi:https://doi.org/10.1136/bmjopen-2016-014998

 PubMed Web of Science ®Google Scholar

Wickham, H., Miller, E., & RStudio (2020). haven: Import and export ‘SPSS’, ‘Stata’ and ‘SAS’ files (2.3.1) [Computer software]. https://CRAN.R-project.org/package=haven

 Google Scholar