Figures & data
Figure 1. A comparison between measured (hydrophone measurements) and simulated (Rayleigh-Sommerfeld and simplified models) acoustic intensity and pressure distributions is shown for (A) a sectored tubular transducer along the angular position, and a planar transducer along (B) the axial range and (C) longitudinal distance. (B) and (C) are reproduced from Lafon C et al. (Cylindrical thermal coagulation necrosis using an interstitial applicator with a plane ultrasonic transducer: in vitro and in vivo experiments versus computer simulations. Int J Hyperthermia 2000;16:508–22). The transducer tubes were sectioned longitudinally to have two active sectors (120°). Thermal simulations are shown for transurethral prostate hyperthermia/ablation by (D) planar and (C) tubular transducer computed using finite difference (FDTD) methods (recreated from Wootton JH et al. (Prostate thermal therapy with high intensity transurethral ultrasound: The impact of pelvic bone heating on treatment delivery. Int J Hyperthermia 2007;23:609–22)). Acoustic energy in panels (D) and (E) were calculated using the rectangular radiator method and the geometric approximation in Equation 2, respectively.
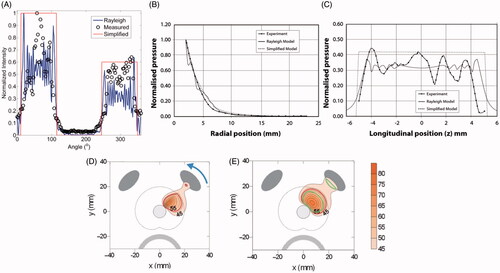
Figure 2. (A) Temperature profile through central slice of a dual-sectored transurethral ultrasound as computed by a transient temperature model. Boundaries of the predicted ablation zone are shown when using a constant attenuation (dashed line) and thermal dose-dependent increase in attenuation. Models that assume a constant attenuation coefficient predict larger ablation zones and lower maximum temperatures. (B) MR image of ex vivo vertebra ablated with an interstitial ultrasound applicator and (C) temperature profile computed with theoretical modelling employing parameters similar to the experimental case. The theoretical model included dynamic changes in tissue attenuation and accounted for reflection and transmission of energy at the soft tissue–bone interface. The computed extent of region experiencing 20 °C rise (solid line) is in good agreement with experimental measurements (dashed line) obtained using MRTI. (B) and (C) are reproduced from Scott SJ, et al. (Interstitial ultrasound ablation of tumors within or adjacent to bone: Contributions of preferential heating at the bone surface. Proc SPIE, Energy-based treatment of tissue and assessment VII, 2013:85840Z–Z).
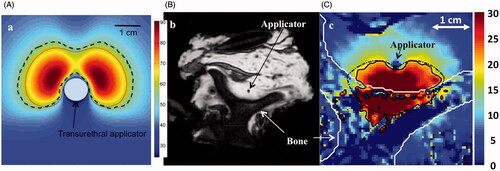
Figure 3. Comparison of patient-specific 3D FEM thermal models with clinical thermometry data: (A) transient temperatures and (B) T50. (C) Comparison between MRTI data and model-based temperature measurements is shown in representative axial slices during ablative heating in tissue mimicking gel phantoms. (C) is reproduced with permission from Burtnyk M, et al. (3D conformal MRI-controlled transurethral ultrasound prostate therapy: Validation of numerical simulations and demonstration 306 in tissue-mimicking gel phantoms. Phys Med Biol 2010;55:6817–39. DOI: 10.1088/0031-9155/55/22/014).
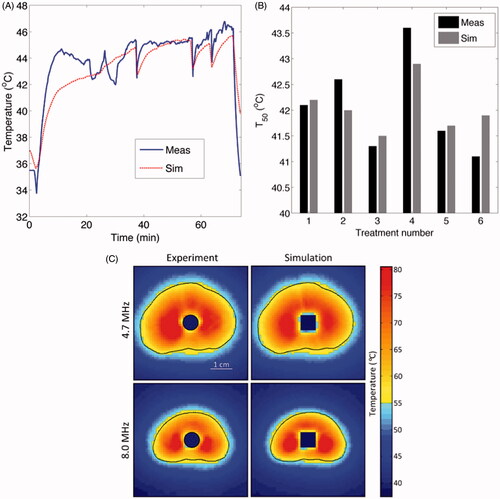
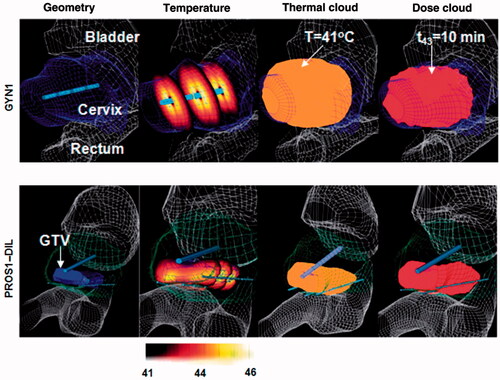
Figure 4. Patient-specific thermal models employed for optimisation and planning of hyperthermia treatments for cervical (top row) and prostate tumours where heating applicators with multiple transducer elements were deployed by endoluminal (cervix) and interstitial (prostate) placement. Case geometries and FEM meshes were constructed from CT scans which were segmented to delineate critical organs, tumour targets and applicator positions. Reproduced from Chen X et al. (Optimisation-based thermal treatment planning for catheter-based ultrasound hyperthermia. Int J Hyperthermia 2010;26:39–55).