Optimisation of the coagulation zone for thermal ablation procedures: A theoretical approach with considerations for practical use

Figures & data

Figure 1. Tumour sphere (shaded grey; tumour centre T and tumour radius r_t), safety margin sphere (non-shaded; safety margin s, centre C* (= T) and radius r_c*) and coagulation centre C with ECC (marked as blue line); r_c* = r_t + s and ECC = √(). Since the tumour centre and coagulation centre are always defined in the x/y-plane, the coagulation centre always has the coordinate C (e_x, e_y, 0).

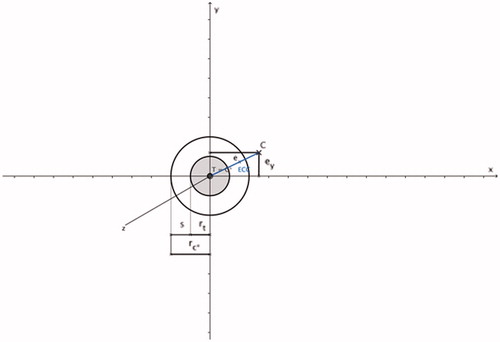
Figure 2. Spherical coagulation zone (shaded in yellow; coagulation centre C), coagulation radius r_c and applicator (marked in red). The direction of the applicator shaft (marked as a red line) is always defined in the x-axis direction; the applicator shaft crosses the coagulation centre C and the applicator tip (marked as a red arrowhead) ends at the surface point P_c on the coagulation margin; the coagulation centre is always defined in the x/y-plane.

Figure 3. Coagulation radius r_c of the optimised coagulation zone (shaded in yellow; coagulation centre C) can be calculated: r_c = ECC + r_t + s. Based on Figures 1 and 2.

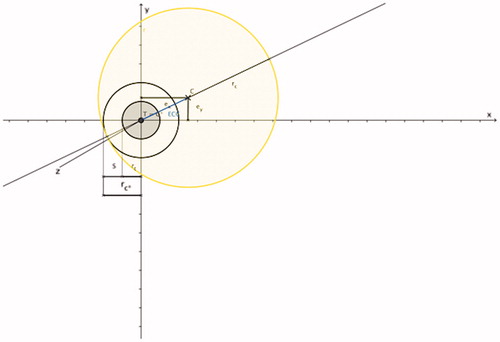
Figure 4. PAO indicates the radial distance in x-axis direction (applicator shaft direction) between surface point P_c on the coagulation margin and surface point P_t on the tumour margin: PAO = ECC + e_x + s. Based on Figures 1, 2 and 3; PAO is the radial distance between two work planes (work plane E_t perpendicular to the x-axis intersecting surface point P_t and work plane E_c perpendicular to the x-axis intersecting surface point P_c).

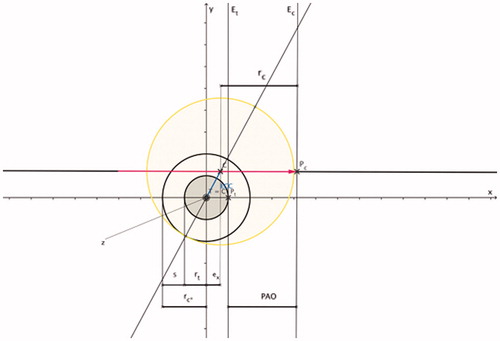
Figure 5. Feasibility of CT-guided thermal ablation by using 3D image post-processing with definition of the master image slice. (A–C, E, F) Standard image planes (transversal, coronal and sagittal). (D, G, H) Master image slice. Positioning of the applicator using standard image planes (A–C). In the standard image planes, the entire course of the applicator shaft (A, E), as well as a fictive tumour centre (white X) (F) did not appear in one single image slice. After individual image angulation the entire course of the applicator shaft as well as the fictive tumour centre (white X) became obvious in one single image slice (master image slice) (D, G, H) with x-axis and y-axis as defined in the Cartesian coordinate system. The direction of the x-axis (red) defined the direction of the applicator shaft; the y-axis (yellow) was defined as being perpendicular to the applicator shaft. In the master image slice, the distance between the applicator shaft and the tumour centre (white X) defines e_y (green) (H).

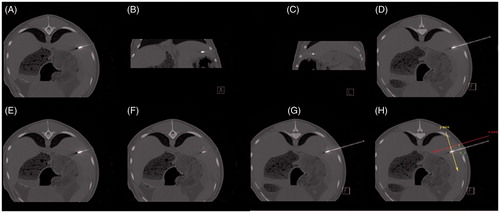
Figure 6. PAO_spec indicates the radial distance in x-axis direction (applicator shaft direction) between the applicator tip (P_spec) and the surface point P_t on the tumour margin: PAO_spec = CC + e_x – r_t.Based on Figures 1–4; ellipsoid coagulation zone (shaded in green; applicator (marked in orange); PAO_spec is the radial distance between two work planes (work plane E_t is perpendicular to the x-axis and intersects with surface point P_t and work plane E_spec is perpendicular to the x-axis and intersects with surface point P_spec); CC is the distance between the projection of the site of the coagulation short diameter on the applicator shaft (C) and the applicator tip (P_spec); the front margin (FM) is the distance between the distal edge of the coagulation zone (P_{c_spec}) and the applicator tip (P_spec).

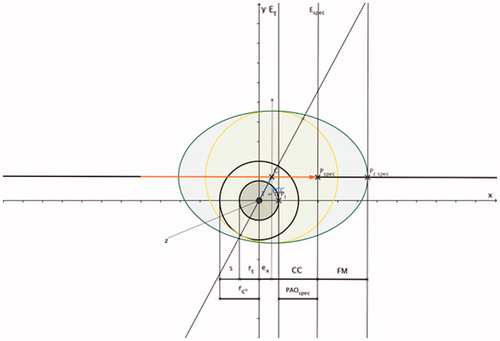
Table 1. Optimised coagulation zone for a tumour diameter of 1 cm (3 cm) and a safety margin of 0.5 cm for spherical coagulation shapes.

	ECC (cm)	r (cm)	d (cm)	V (cm^3)	PAO (cm)
Tumour	–	0.5 (1.5)	1.0 (3.0)	0.5 (14.1)	–
Optimised coagulation zone No dislocation of the coagulation centre in relation to the tumour centre (safety margin sphere)
ex = 0 cm, ey = 0 cm	0 (0)	1.0 (2.0)	2.0 (4.0)	4.2 (33.5)	0.5 (0.5)
Dislocation of the coagulation centre in relation to the tumour centre in the applicator shaft direction
ex = 0.5 cm, ey = 0 cm	0.5 (0.5)	1.5 (2.5)	3.0 (5.0)	14.1 (65.4)	1.5 (1.5)
ex = 2.0 cm, ey = 0 cm	2.0 (2.0)	3.0 (4.0)	6.0 (8.0)	113.1 (268.1)	4.5 (4.5)
Dislocation of the coagulation centre in relation to the tumour centre perpendicular to the applicator shaft direction
ex = 0 cm, ey = 0.5 cm	0.5 (0.5)	1.5 (2.5)	3.0 (5.0)	14.1 (65.4)	1.0 (1.0)
ex = 0 cm, ey = 2.0 cm	2.0 (2.0)	3.0 (4.0)	6.0 (8.0)	113.1 (268.1)	2.5 (2.5)
Dislocation of the coagulation centre in relation to the tumour centre in the applicator shaft direction and perpendicular to the applicator shaft direction
ex = 0.5 cm, ey = 0.5 cm	0.7 (0.7)	1.7 (2.7)	3.4 (5.4)	20.8 (83.1)	1.7 (1.7)
ex = 2.0 cm, ey = 2.0 cm	2.8 (2.8)	3.8 (4.8)	7.7 (9.7)	235.0 (471.5)	5.3 (5.3)

ECC, Eccentricity of the coagulation centre; r, optimised coagulation radius; d, optimised coagulation diameter; V, optimised coagulation volume; PAO, parallel offset indicates the radial distance in x-axis direction (applicator shaft direction) between surface point P_c on the coagulation margin and surface point P_t on the tumour margin.

Figure 7. Relationship between ECC and the optimised coagulation volume. The larger the ECC, the larger the optimised coagulation zone; the optimised coagulation volume is larger for ellipsoid coagulation shapes (B), compared with spherical coagulation shapes (A); for identical numerical values of ECC, PAOs (PAOs_spec) can be different depending on the dislocation of the coagulation centre in relation to the tumour centre (see Tables).

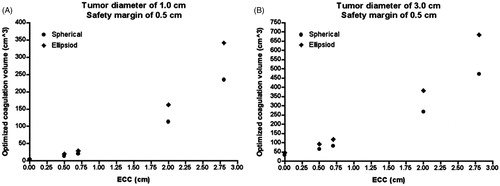
Table 2. Optimised coagulation zone for a tumour diameter of 1 cm (3 cm) and a safety margin of 0.5 cm for ellipsoid coagulation shapes.

	ECC (cm)	Optimised coagulation short diameter^1,2 (cm)	Ellipticity index^2	Coagulation long diameter^2 (cm)	Optimised coagulation volume^3 (cm^3)	Coagulation centre^2 (cm)	PAOspec (cm)
Optimised coagulation zone No dislocation of the coagulation centre in relation to the tumour centre
e^x= 0 cm, e^y= 0 cm	0 (0)	2.0 (4.0)	0.7 (0.7)	2.7 (5.4)	5.7 (45.2)	1.2 (2.2)	0.7 (0.7)
Dislocation of the coagulation centre in relation to the tumour centre in the applicator shaft direction
e^x= 0.5 cm, e^y= 0 cm	0.5 (0.5)	3.0 (5.0)	0.7 (0.7)	4.3 (7.1)	20.3 (92.9)	1.7 (2.5)	1.7 (1.5)
e^x= 2.0 cm, e^y= 0 cm	2.0 (2.0)	6.0 (8.0)	0.7 (0.7)	8.6 (11.4)	162.1 (382.0)	2.7 (3.0)	4.2 (3.5)
Dislocation of the coagulation centre in relation to the tumour centre perpendicular to the applicator shaft direction
e^x= 0 cm, e^y= 0.5 cm	0.5 (0.5)	3.0 (5.0)	0.7 (0.7)	4.3 (7.1)	20.3 (92.9)	1.7 (2.5)	1.2 (1.0)
e^x= 0 cm, e^y= 2.0 cm	2.0 (2.0)	6.0 (8.0)	0.7 (0.7)	8.6 (11.4)	162.1 (382.0)	2.7 (3.0)	2.2 (1.5)
Dislocation of the coagulation centre in relation to the tumour centre in the applicator shaft direction and perpendicular to the applicator shaft direction
e^x= 0.5 cm, e^y= 0.5 cm	0.7 (0.7)	3.4 (5.4)	0.7 (0.7)	4.8 (7.7)	29.1 (117.6)	2.0 (2.6)	2.0 (1.6)
e^x= 2.0 cm, e^y= 2.0 cm	2.8 (2.8)	7.7 (9.7)	0.7 (0.7)	11.0 (13.9)	341.5 (684.8)	3.0 (3.5)	4.5 (4.0)

ECC, eccentricity of the coagulation centre; optimised coagulation short diameter is defined as the maximum coagulation diameter perpendicular to the applicator shaft direction; ellipticity index is defined as the ratio of optimised coagulation short diameter and coagulation long diameter; coagulation long diameter is defined as the maximum coagulation diameter in the applicator shaft direction; coagulation centre is defined as the distance between the projection of the site of the optimised coagulation short diameter on the applicator shaft and the applicator tip; PAO_spec, parallel offset_spec indicates the radial distance in the applicator shaft direction between the applicator tip and surface point P_t on the tumour margin.

¹Absolute values according to Table 1 since the optimised coagulation short diameter for ellipsoid coagulation shapes is identical to the optimised coagulation diameter for spherical coagulation shapes.

²Bold numbers come from the commercial information of a microwave ablation system, non-bold numbers are extrapolated accordingly.

³Calculated according to Equation 15.

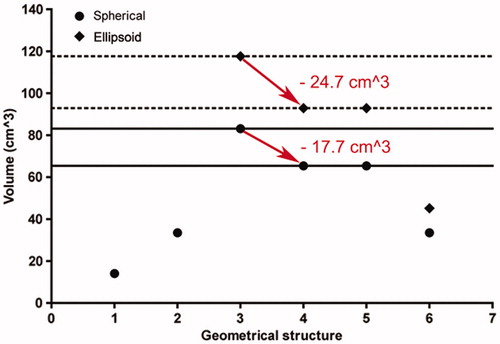
Figure 8. Minimisation of the optimised coagulation zone after positioning of the applicator without the need for repuncture (neutralisation of e_x). 1 (on the geometrical structure axis), tumour sphere (diameter of 3.0 cm); 2, safety margin sphere (safety margin of 0.5 cm); 3–6, optimised coagulation zone for spherical (point) and ellipsoid (diamond) coagulation shapes (3, e_x = 0.5 cm and e_y = 0.5 cm; 4, e_x = 0 cm and e_y = 0.5 cm; 5, e_x = 0.5 cm and e_y = 0 cm; 6, e_x = 0 cm and e_y = 0 cm). After neutralisation of e_x (e_x = 0 cm) (red arrow), for spherical (ellipsoid) coagulation shapes an unnecessary coagulation volume of 17.7 cm³ (24.7 cm³) can be eliminated by slightly adjusting the applicator shaft by pulling back or pushing forward (for spherical (ellipsoid) coagulation shapes by reduction of PAO (PAO_spec) from 1.7 cm to 1.0 cm (1.6 cm to 1.0 cm)).