Measurement and Mind: Unveiling the Self-Delusion of Metrification in Psychology

ABSTRACT

This paper critically evaluates the quantification of psychological attributes through metric measurement. Drawing on epistemological considerations by Immanuel Kant, the development of measurement theory in the natural and social sciences is outlined. This includes an examination of Fechner’s psychophysical law and the fundamental criticism initially raised by von Kries. The distinction between theoretical and practical measurability is illuminated, addressing the question of equality within mental entities ($\mathrm{\Psi }$) and their measures ($\mathit{\theta }$). Psychometric scaling procedures such as Rasch scaling are argued to enable interval-scaled quantification on a real number line $\mathit{\theta }$, but they are insufficient to establish a genuine interval scale level of $\mathrm{\Psi }$. Instead, the values of $\mathit{\theta }$ should be regarded as qualitative statements that indicate ordinal relationships within $\mathrm{\Psi }$. Two principles of scaling – the Guttman “model” and the Rasch model – are introduced, with their theoretical foundations explained, referencing the Rasch paradox. In the empirical section, data simulation is conducted to illustrate the Rasch paradox and to substantiate the theoretical considerations of the article. The research underscores the significance of linguistic analysis in understanding quantitative claims, suggesting a shift toward ordinal quantification within psychological measurement, drawing upon the linguistic principle of localism. Spatial metaphors are argued to play a central role in human language, even in natural sciences like physics, suggesting that systematic analysis of human language could offer a valuable method for the quantitative analysis of psychological attributes.

KEYWORDS:

• Rasch Model
• scale level
• scaling
• ordinal measurement
• interval scale
• metrification
• Item Response Theory
• theory of science

Introduction

This article is dedicated to the overarching topic of an objective quantification of psychological characteristics. We will specifically deal with the question of the measurement level to be achieved and appropriately interpreted in such a quantification approach, for example, as proposed quite prominently by Stevens (1946, 1958) for social science measurement theory. However, it is precisely this Steven’s taxonomy of scale levels that has been even before Stevens and continues to be the subject of controversial contributions and debates in scientific psychology (see e.g. Feuerstahler, 2023; Lord, 1953; Mausfeld, 1994; Trendler, 2009; von Kries, 1882; Zand Scholten & Borsboom, 2009, just to name a few). The single contributions touch on fundamental epistemological questions and questions of scientific measurement theory and reach so far into the history, not only of the subject of psychology, that it must be stated that the controversy about the measurement of the Psychic and its scale level has ultimately accompanied the subject of psychology throughout its scientific development.

Thus, since the beginnings of scientific psychology, specifically with the foundation of Fechner’s psychophysics (see Fechner, 1858), there has been an ongoing, lively, and sometimes controversial debate on the idea of measurement in psychology (e.g Campbell, 1921; Cliff, 1992; Humphry, 2011; Kyngdon, 2008b, 2011b; Maraun, 1998; Markus & Borsboom, 2012; Maul et al., 2016; Michell, 2005, 2006, 2021; Saint-Mont, 2012; Salzberger, 2013; Schönemann, 1994; Sijtsma, 2012; Thomas, 2020; Trendler, 2009, 2019b; Uher, 2018, 2021b, 2022; Velleman & Wilkinson, 1993, just to name some). There are so many (more) contributions in the literature on this topic of measurement, not just psychological measurement, and its appropriate level that a more or less complete bibliography alone could easily go beyond the bounds of a journal article. We will therefore limit ourselves here to a few basic sources that address central concepts and ideas, knowing full well that some readers may miss something here.

Although there seems to be broad acceptance that Fechner’s approach to quantifying the Psychic ($\mathrm{\Psi }$) established a fundamental paradigm shift toward quantification in the history of psychology (e.g. Michell, 1999), there is only limited consensus about the particular conclusions in terms of substance science interpretation derived from this paradigm; for example, with respect to the level of measurement of the Psychic ($\mathrm{\Psi }$), or in modern language: psychological traits, on a so-called “metric” interval scale. This paper first references this fundamental critique of the metric measurability as well as interpretation of psychological variables and, secondly, bridges current issues of scalability and the extent to which outcome variables can be interpreted on certain scale levels, as prominently proposed, for example, by Stevens (1946).

Since the measurement principles of scientific psychology were strongly oriented toward those of the natural sciences when they were founded (e.g. Cornejo & Valsiner, 2021), we consider it appropriate in this essay to embed the controversy surrounding the measurement of the Psychic in a somewhat larger, also scientific-theoretical framework. This will show that even the seemingly rock-solid foundation of, for example, metric measurement in physics can also be seen as an implicit circular argument, at least from a strictly epistemological perspective. With regard to this statement, which may seem somewhat surprising to the reader at this point, reference is made, for example, to comments made by Böhme (1976) on the foundations of quantification in the natural sciences as already discussed in Duhem (1908).

We shall begin by examining the theoretical foundations of measurement, starting with its application in the domain of natural sciences. Through a concise outline, we will highlight key milestones in the historical development of the concept of measurement, both in general and with a focus on psychology. In addition, we will delve into two dominant scaling models extensively utilized in psychometrics, presenting their implications and paradoxes.

In order to adequately address the specific questions about measurement in psychology in this paper and to embed them in a broader scientific theoretical framework, this paper is organized as follows. In the following section, we will outline the social origins and scientific theoretical foundations of measurement. In the form of a brief outline, few milestones and examples in the historical development of the concept of measurement in general and its embedding in social developments over the last centuries will be presented (Frängsmyr et al., 1990). We will not go into too much detail about the technical aspects of physical measurement operations in the natural sciences but rather concentrate on the epistemological implications. Second, we will then address some central aspects of approaches to measuring $\mathrm{\Psi }$. Third, we will specifically address two basic scaling procedures that are widely used in psychometrics and present their implications and paradoxes in the context of the measurement principle of psychological research.

In a final empirical part, a small simulation study will be conducted to illustrate the theoretical issues presented in the previous sections. In the concluding discussion, we will outline the main implications for practical measurement tasks in psychology and give some suggestions for the interpretation of scaling results in psychological and social science research. The prospects for further research will be presented as a conclusion.

Human perception, social discourse and the rise of the ideal of quantification in the natural sciences

Human perceptions and the social exchange regarding our perceptions about the “external world” are fundamental to our collective existence. When individuals discuss their perceptions of the world, they frequently employ spatial metaphors (e.g., “by far” the best performance, “highest” price, hitting a new “low,” etc.), suggesting that such linguistic spatial metaphors mirror underlying mental metaphors – a hypothesis supported by empirical evidence (see e.g., Casasanto & Bottini, 2014; Fischer & Shaki, 2014; Starr & Srinivasan, 2021, for a review). These findings are central to our present paper. First, they address the fundamental question of whether there is any possibility of “objectivity” in shared human perceptions – in essence, “what can we know” (with certainty)? Secondly, such spatial metaphors resonate with Kant’s thesis that the fundamental structures of perceived reality – space and time – are prescribed a priori in our way of perceiving the world. Beginning with an exploration of the objectification of perception, we will discuss these two central aspects in the theoretical sections of this paper.

The onset of the Enlightenment sparked a growing interest in objective methods of perceiving and measuring the world. In this briefly outlined context, the shift toward “the rational” view of the world marked the beginning of humans’ objective measurement of the shared environment, laying the foundation for systematic natural sciences (e.g., Frängsmyr et al., 1990; Mason, 1956). This almost revolutionary commencement of human-led measurement of the shared environment not only influenced the emerging scientific community but also left a profound impact on broad segments of society and public discourse. It continues to inspire nonscientific authors to produce reflective literary works on the origins and ascent of measuring the external world (see e.g., Kehlmann, 2007). Francis Bacon (1561–1626) is often cited in contemporary writings on the history of science as a prominent figure symbolizing the shift toward new scientific paradigms at the end of the Middle Ages (e.g., Böhme, 1993; Mason, 1956; Meinel, 1984). With his Novum organon scientiarum, published around 1620 (see Bacon, 1762, for an available reference), Bacon established a new logic of scientific invention. In his work, Bacon documents instruments and principles for arriving at new (scientific) discoveries in orderly, systematic steps (e.g., Meinel, 1984). However, it must be critically noted that (1) there were already scientifically-based inventions before Bacon (gunpowder, the compass, …) and that (2) Bacon’s role as the founder and representative of a new scientific approach is overstated (e.g., Frost, 1927; von Liebig, 1874). For instance, in one treatise, von Liebig (1874) highlights Bacon’s critical perspective on the empirical research method, noting that active natural scientists of his time knew nothing of Bacon, and that there is to this day no clear evidence of his active influence on natural science (von Liebig, 1874). In this context, Mason (1956) observes that Bacon, serving as Lord Chancellor of England under King James I, was not primarily a natural scientist. Instead, he was among the first to recognize the historical importance and potential of science, as well as its transformative role. Consequently, he endeavored to engage others in science to actualize these potentials (Mason, 1956, p. 110). In this vein, the innovative perspective introduced by Francis Bacon can be perceived at a meta-level as the groundwork for a novel scientific theory (Böhme, 1993). Specifically, this entailed the inception or promotion of a new methodology for fostering innovations and advancing knowledge.

According to Bacon, scientists were thus no longer merely connoisseurs in regard to a fixed canon of knowledge and Aristotelian logic, but publicly exposed members of a newly forming society that was increasingly turning toward the rational, who had to (constantly) expand the corpus of collective knowledge by adding new contributions to (scientific) knowledge. This new and now also critical view of “new” science is prototypically demonstrated much later in modern times by Max Weber who stated: “Every scientist knows that what he has contributed to knowledge will be obsolete in 10, 20, 50 years” (Weber, 1919, p. 14). After almost 300 years of cultivating and maturing the principles of enlightened natural sciences since Bacon, Max Weber provides a disillusioned analysis of the progress made by science, particularly as it manifests in the living conditions of the modern age. For Weber, the “disenchantment of the world” [Entzauberung der Welt] (Weber, 1919, p. 16) is the fate of this modern age, characterized by rationalization and intellectualization, which are now taken for granted as core elements of science. Thus, for Weber, the progress in knowledge and technology associated with systematization and rationalization also implies an increasing responsibility of science toward society, particularly in ensuring that what emerges from scientific work is considered important in the sense of being “worth knowing” [wissenswert] (Weber, 1919, p. 21) – not only for the individual but also for society.

Epistemological distinction between intensive and extensive measures

The initiation of systematization in acquiring scientific knowledge, often attributed to Francis Bacon, is evident in the growing interest in not only the practical aspects of measurement but also in its epistemological implications. This interest pertains to understanding both the nature of what is being measured and the properties of these measurements. Around a century after Bacon, it was Immanuel Kant (1724–1804), who, in his seminal 1781 work “Critique of pure reason” [Critik der reinen Vernunft] engaged with Aristotelian concepts of quality and quantity. Within his “Axioms of perception” [Axiomen der Anschauung] and “Anticipations of perception” [Anticipationen der Wahrnehmung] (Kant, 1781, pp. 162–176) he distinguished between intensive and extensive measures of natural entities (see also Böhme, 1974). The core idea behind the distinction between extensive and intensive measures [intensive Gröẞen] stems from Kant’s thesis that the fundamental structures of reality, space, and time, are prescriptions of our way of perceiving the world (a priori). Extensive measures [extensive Gröẞen] are not intrinsic properties of things themselves; rather, they are ascribed to things relative to our mode of cognition and perception, emerging from our own minds as a distinctly human form of perception. In Kant’s own words, “All phenomena contain, in their form, a perception in space and time, which is their overall a priori basis. They can therefore be apprehended in no other way, i.e., they cannot be taken up into empirical awareness …” [Alle Erscheinungen enthalten der Form nach eine Anschauung im Raum und Zeit, welche ihnen insgesammt a-priori zum Grunde liegt. Sie können also nicht anders apprehendirt, d. i. ins empirische Bewusstsein aufgenommen werden …] (Kant, 1911, p. 148) or “I call an extensive measure the one in which the conception of the parts makes the conception of the whole possible … “[Eine extensive Grösse nenne ich dieienige, in welcher die Vorstellung der Theile die Vorstellung des Ganzen möglich macht …] (Kant, 1781, p. 162). It is precisely this last quote from Kant’s work that to a certain extent anticipates Fechner’s (Fechner, 1858) approach to quantifying the Psychic and also points the way to current conceptualizations of (fundamental) measurement such as those later undertaken by von Helmholtz (1887); Hölder (1901) to link the definition of measurement to real objects.

Intensive measures, on the other hand, are, as anticipations of perception, subjective imaginations which correspond to real objects insofar as they provide sensation. In Kant’s own words, “The principle which anticipates all perceptions, as such, is called thus: In all phenomena the sensation, and the real which corresponds to it in the object, (realitas phaenomenon) has an intensive magnitude, i.e., a degree.” [Der Grundsatz, welcher alle Wahrnehmungen, als solche, anticipirt, heiẞt so: In allen Erscheinungen hat die Empfindung, und das Reale, welches ihr an dem Gegenstande entspricht, (realitas phaenomenon) eine intensive Grösse, d. i. einen Grad.] (Kant, 1781, p. 166).

Kant’s early epistemological distinction between intensive and extensive measures finds its equivalent in current natural science, particularly in physics and metrology. Extensive measures, such as length and weight, are understood to depend on the size of the system under consideration, representing properties empirical objects can show, with variations in magnitude (Hölder, 1901; Trendler, 2009; von Helmholtz, 1887). Kant termed these measures as appearances of the real world. Additive metric measurement for these extensive measures is based a priori on the peculiarity of our human perceptual apparatus, adapted to perceive ourselves and our environment in three-dimensional spatial and temporal continuity. Such additivity results from the perceived additive relationship of the properties of empirical objects, observed in operations such as placing weights in the same weighing pan or aligning measuring rods (see e.g. Sherry, 2011, p. 518). Aristotle already recognized that length and weight have parts, allowing for their addition and subtraction in empirical contexts. Thus, the metric measurement of extensive quantities is reduced to counting concatenated units, equivalent in their implied order relationship (Hölder, 1901). For instance, the “International Prototype Metre”, manufactured in 1889 as a platinum-iridium alloy scale, was defined by the French National Assembly as the forty-millionth part of the earth’s meridian passing through Paris, serving as one meter (cf. Hoppe-Blank, 2015, p. 7).

On the other hand, temperature, distinct from heat or thermal energy and measured in degrees Celsius or Fahrenheit, is considered an intensive quantity. Intensive quantities are physical measures that remain constant regardless of the amount of substance present in a system, unlike extensive quantities, which vary in proportion to the system’s size. While humans can measure extensive quantities, like length, using manifest reference objects and natural units, the measurement of other physical quantities, such as temperature, is not as straightforward due to the lack of perceptible units without additional assumptions. Unlike length, temperature scales cannot be divided into countable parts, making it nontrivial to determine whether thermometer measurements can be added or subtracted. For example, Sherry (2011) pointed out that a metric interpretation of temperature measurement relies on theoretical model assumptions (see also Chang, 1995, 2004), particularly in substance science, regarding the physical properties of the measuring liquids used, typically alcohol or mercury.

Circular reasoning when measuring in science

According to Chang (2004), the realization that a well-founded model or theory of the physical properties of the measuring liquids is required as a basis for classical thermometers can be traced back to early observations by the Dutch physicist Herman Boerhaave (1668–1738). Boerhaave, who possessed two thermometers with mercury and alcohol, both made by Daniel Gabriel Fahrenheit, noted discrepancies in measured values from thermometers with different measuring liquids. Despite having the same scale endpoints for the freezing and boiling points of water on a 100-point scale, Fahrenheit was initially unable to explain the different temperature values for empirically identical temperatures. The realization that these discrepancies were ultimately due to the varying expansion coefficients of the measuring liquids, which change depending on the temperature level, was not self-evident in Boerhaave and Fahrenheit’s time. As Chang (2004) further explains, the standard calibration procedure for thermometers at that time just involved establishing two scale endpoints on the column of liquid used for measurement, such as the freezing and boiling points of water, while implicitly assuming a linear relationship between temperature rise and liquid expansion. However, this overlooks the fact that the entire principle of temperature measurement is justified only by the model assumption of a constant expansion coefficient over the entire measurement range, which is made a priori within the framework of scientific theory. For such a theory to serve as a valid basis for measurement, empirical evidence would first need to be established. However, this would require a proven thermometer. This problem of the epistemological circularity of measurement definition, referred to by Chang (1995, 2004) as “nomic measurement,” also exists in other areas of physics and the natural sciences in general. Moreover, within the topic of measuring energy in quantum mechanics Chang (1995) pointed to the fact that the direct use of a physical law, derived from substance science theory, for the purpose of measurement creates a problem of circularity. The law (the theory) needs to be empirically tested in order to ensure the reliability of measurement, but the testing of the theory requires that we already know about the quantitative properties of the quantity to be measured. Therefore, the seemingly simple statement, typically used within supposedly universally valid and broad definitions of measurement, that a measurement $\mathit{X}$ of the set $\mathit{M}$ belongs to the system $\mathit{S}$, only makes sense from the point of view of substance science if the system ($\mathit{S}$) has already been classified as a part of $\mathit{M}$ via a “justified” proposition based on theory (Van Fraassen, 2008). In this respect, the statement remains theoretical and ultimately depends on our (a priori) accepted theories and classifications of physical, and indeed mental or perceptual systems. If our theories change, the conditions for the truth of this statement also change (cf. Van Fraassen, 2008, p. 143). Admittedly, the theory dependence of measurement statements does not manifest as conspicuously in the context of established measurement procedures that are widely accepted and taken for granted. Consider the example of measuring temperature: in everyday contexts, the practical benefits of using thermometers are generally acknowledged, even in the absence of a deep epistemological understanding, given the relatively well-established and stable underlying theory. However, from a strictly epistemological standpoint, the theoretical underpinnings of measurement statements remain crucial. This interdependence becomes particularly evident in scenarios where a theory is novel and potentially at odds with an existing framework addressing the same phenomenon. An extended or rather alternative definition of measurement that takes this into account, is given by Van Fraassen (2008), according to which “measurement is an operation that locates an item, already classified as in the domain of a given theory, in a logical space, provided by the theory to represent a range of possible states or characteristics of such items” (Van Fraassen, 2008, p. 164). In such cases, the behavior of any measurement device falls within the domain of the a priori theory itself, and the criteria for interpreting it as a physical, observable correlate of the measurement are described in terms of the theory itself, which constitutes a circular reasoning, at least from a strict epistemological perspective (see also e.Böhme, 1976; Duhem, 1908). From the negation of this obvious paradox, which in the end is only covered by the acceptance and stability of the background theories forming the respective measurement context, the positivist illusion was derived that we could describe the measurement processes and their results free of any theoretical content (Van Fraassen, 2008).

Measuring the psychic, and the illusion of metric scale levels for $\mathit{\psi }$

As discussed in the previous section, even in the natural sciences like physics, the issue of circularity can arise during the establishment of unique measurements (metrification) if their operationalization relies on observed physical laws in the empirical domain. Furthermore, for an extensive measure, identifying units of equal magnitude is a necessary precondition for quantification and fundamental measurement (cf. Hölder, 1901; Trendler, 2019a; von Helmholtz, 1887). This process of fundamental measurement, which hinges on units of equal magnitude, essentially boils down to the simple act of counting concatenated units. But more or less throughout the last around 100 hundred years of attempting to develop psychology as a quantitative science (Campbell, 1921) there were doubts raised if and if so how that might be accomplished (Díez, 1997a, 1997b).

Confusion in this debate may stem from the ambiguous use of the term “metric”. Adroher et al. (2018), based on a systematic literature review, conclude that “metric” is employed in various ways, without a consensus on whether its meaning implies interval scale properties or “only” ordinal or ordered scales. To foster clarity, we draw on the definition of “metric” in a metric space from the subfield of topology in mathematics.

Let $\mathit{X}$ be a non-empty set. A mapping $\mathit{d}:\mathit{X}\times \mathit{X}\mapsto \mathbb{R}$ is called a metric on $\mathit{X}$ if for all $\mathit{x},\mathit{y},\mathit{z}\in \mathit{X}$ the following conditions hold:

(1) $({\mathit{C}}_1)\mathit{d}(\mathit{x},\mathit{y})=0\iff \mathit{x}=\mathit{y},$(1)

(2) $({\mathit{C}}_2)\mathit{d}(\mathit{x},\mathit{y})=\mathit{d}(\mathit{y},\mathit{x})$(2)

(3) $({\mathit{C}}_3)\mathit{d}(\mathit{x},\mathit{z})\le \mathit{d}(\mathit{x},\mathit{y})+\mathit{d}(\mathit{y},\mathit{z})$(3)

where $\mathit{d}$ is a mapping function and the pair $(\mathit{X},\mathit{d})$ is called metric space.

Despite the precision and clarity provided by a mathematical definition of a metric, it is essential to clarify that this definition initially applies solely to the mathematical number space, such as the set of real numbers $\mathbb{R}$. This space provides a numerical representation for the measured values of extensive physical quantities like length or mass. This representation aligns with the classical concept of measurement, which involves counting units and is justified by the potential for concatenating physically tangible objects.

For the measurement of extensive quantities in physics such as mass and length Hölder (1901), was able to prove that precisely the given additive connection of these physical characteristics in the tangible, phenomenological object domain implies a 1:1 connection to the mathematical metric space or system of positive real numbers. This fact was first formalized by other authors for the mathematical field, such as Bertrand Russell (cf. Russell, 1903/2010), and later called isomorphic mapping for the field of social-scientific, psychological measurement in the context of the so-called representation theory of measurement (cf. Michell, 1993; Stevens, 1958; Weitzenhoffer, 1951). In his tracing of the development of the representational theory of measurement, Michell (2021) points out that this originally developed from the endeavor of mathematics to establish the subject as independent of its applications in empirical science and was picked up later in particular by authors like Stevens (1946, 1958) to give psychology the status of a quantitative science through the reconstruction of measurement as the numerical coding of psychological characteristics from the phenomenological domain.

The fundamental concept underlying the representational theory of measurement is that of a relational system or structure. A relational system consists of a finite set of elements, referred to as the domain of the relational system, and relationships between these elements. In his seminal work on scientific mathematical models, Tarski (1954) provided a comprehensive definition of a relational system, framing it within the context of a mathematical structure. Tarski (1954) defines a relational system as follows, while noting that such relational systems are also termed algebras:

By a relational system, we understand an arbitrary system (sequence) $\mathrm{\Re }=<\mathit{A},R_0,\dots ,R_{\xi },\dots >$ in which $\mathit{A}$ is a non-empty set, $R_0,\dots ,R_{\xi },\dots$ are finitary relations, and each relation $R_{\xi }$ is included in $A^{v_{\xi }}(R_{\xi }\subseteq A^{v_{\xi }})$ where $v_{\xi }$ is the rank of $R_{\xi }$; the type of the sequence $<R_0,\dots ,R_{\xi },\dots >$ is called the order of $\mathrm{\Re }$

(Tarski, 1954, p. 573)

According to the foundations of the subdiscipline of topology in mathematics (see Fréchet, 1906; Hausdorff, 1914, for early references), which focuses on formal defining such metric spaces, the set of real numbers $\mathbb{R}$ (as part of $\mathbb{C}$) forms a universal numerical structure, serving as a metric space. This structure enables the representation as a relational system of any one-dimensional quantitative entity within a formal framework.

In the representation theory of measurement, particularly within the context of social science measurement, two types of relational systems are posited: an empirical relational system (ers) and a numerical relational system (nrs). These systems are crucial to the framework of the representation theory, necessitating a plausible and, importantly, empirically supported mapping function to connect the empirical structure with the numerical one.

Thus, despite the precision and clarity of the mathematical definitions provided for a metric and metric spaces, it is crucial to acknowledge that these initially pertain only to the numerical relational system (nrs). While such definitions offer a formal framework for the principle of unit counting in measurements, they do not address whether the defined metric is applicable within the empirical relational system $\mathrm{\Psi }$. In this context, a crucial question arises: how can we establish a connection, in terms of a mapping function, between the empirical object domain (relative) and the numerical relational system? This challenge is pertinent for capturing or measuring characteristics like $\mathrm{\Psi }$ that can only be identified indirectly, such as human feelings, mental processes, or attitudes. The strategies employed in psychology to address this issue are diverse and have been integral to the discipline since its inception

An early representative of this question was Gustaf Theodeor Fechner (1801–1887). Fechner’s initial foray into measuring the Psychic, as detailed in his works (see. Fechner, 1858, 1860a, 1860b), was likely driven by the goal of identifying a fundamental unit as the basis for quantifying psychic phenomena $\mathrm{\Psi }$. Indeed, Fechner recognized that pinpointing such a unit was crucial not only for legitimizing the measurement process in psychology by enabling the counting of units, but also understood that psychic measurement necessitated an indirect approach. He compared it to the indirect measurement of temperature in physics, where temperature is inferred from the expansion of a liquid – a process that, in line with Kant’s theory, categorizes temperature as an intensive quantity. In his seminal 1858 essay “The Psychic Measure” (cf. “Das Psychische Maß”; Fechner, 1858), Fechner outlines his measurement methodology, emphasizing the project’s objective as follows:

In fact, it will be shown how our psychic measure in principle amounts to nothing other than the physical, to the counting of how many times the same thing. We would, of course, try in vain to make such a direct count: Sensation does not divide itself into equal inches or degrees that we could count.

[In der That wird sich zeigen, wie unser psychisches Maẞ prinzipiell auf nichts anderes hinauskommt, als auf das physische, auf die Zählung eines Wievielmal des Gleichen. Umsonst freilich würde wir versuchen, eine solche Zählung direct vorzunehmen: Die Empfindung theilt sich nicht in gleiche Zolle oder Grade ab, die wir zählen könnten.]

(Fechner, 1858, p. 2; German spellings as in the original)

Fechner sought to create a connection between mental sensations and physical stimuli by quantifying them with predefined physical and metric units of measurement. In essence, he sought to make mental qualities measurable by defining a fundamental mental unit through a mapping function that connects psychic phenomena ($\mathrm{\Psi }$) with physical phenomena. In fact, Fechner himself described the psychophysical function he identified as a fundamental formula [Fundamentalformel] (see Fechner, 1860b, pp. 9–10) which, on the basis of Weber’s law, formalizes the relationship between the (smallest) units for the psychic experience $\mathrm{\Psi }$ ($\mathit{d\gamma }$), the respective physical unit ($\mathit{d\beta }$) and the actual physical stimulus intensity ($\mathit{\beta }$) measured in the latter units (see Equation 4).

(4) $\mathit{d\gamma }=\mathit{K}\times \frac{\mathit{d\beta }}{\beta }$(4)

Fechner considered the two smallest units $\mathit{d\beta }$ and $\mathit{d\gamma }$ of the two scales $\mathit{\gamma }$ and $\mathit{\beta }$ as differentials. To justify this approach, Fechner (1860b) writes as follows:

The fundamental formula developed at the beginning of the previous Chapter […] is based on experiments on differences which are at the limit of the intelligible. According to this, $\mathit{d\gamma }$ and $\mathit{d\beta }$ can be considered and treated as differentials in it.

Die im Eingange des vorigen Kapitels entwickelte Fundamentalformel […] stützt sich auf Versuche über Unterschiede, welche an der Gränze des Merklichen stehen. Hienach können $\mathit{d\gamma }$ und $\mathit{d\beta }$ in ihr als Differenziale betrachtet und behandelt werden. (Fechner, 1860b, p. 33; German spellings as in the original; the omission refers to the Equation 4(4) $\mathit{d\gamma }=\mathit{K}\times \frac{\mathit{d\beta }}{\beta }$(4) )

Through integration, Fechner arrives at the following equation: 5:

(5) $\mathit{\gamma }=\mathit{K}\times {log}_e\mathit{\beta }+\mathit{C}$(5)

Fechner replaces the integration constant $\mathit{C}$ in Equation 5 by introducing a lower stimulus threshold $\mathit{b}$, below which the sensory intensity $\mathit{\gamma }=0$ – i.e., the person perceives nothing. Mathematically, this corresponds to setting the equation 5 to zero, whereby Fechner uses $\mathit{\beta }=\mathit{b}$, so that the Equation 6 results by resolving to $\mathit{C}$:

$0=\mathit{K}\times {log}_e\mathit{b}+\mathit{C}$

(6) $\mathit{C}=-\mathit{K}\times {log}_e\mathit{b}$(6)

Substituting Equation 6 into equation 5 finally results in the Equation 7 after factoring out and transforming according to the calculation rules for logarithms.

$\mathit{\gamma }=\mathit{K}\times {log}_e\mathit{\beta }-\mathit{K}\times {log}_e\mathit{b}$

$\mathit{\gamma }=\mathit{K}\times ({log}_e\mathit{\beta }-{log}_e\mathit{b})$

(7) $\mathit{\gamma }=\mathit{K}\times {log}_e\left(\frac{\beta }{b}\right)$(7)

In the equations above, $\mathit{\gamma }$ and $\mathit{\beta }$ stand for the psychological and physical scale based on their fundamental units respectively, $\mathit{e}$ is Euler’s number as the basis for the natural logarithm and $\mathit{K}$ is a scaling factor that is directly related to Weber’s constant and therefore varies depending on the sensory modality.

However, perhaps overshadowed by Fechner’s mathematically ingenious derivation, it is often overlooked that this approach relies on a simple yet significant additional assumption. This assumption posits that by mapping the physical stimulus intensities (on the $\mathit{\beta }$ scale), which increase geometrically, onto the arithmetic scale of the $\mathit{\gamma }$ scale, the psychological equality of sensory units across the entire perception continuum is assumed. But, one must honestly state that this assumption lacks empirical substantiation. This assumption parallels somehow the empirically unproven assumption of a linear model when attempting to measure temperature via the (length of) expansion of any measurement liquid at different temperatures (see the above section).

Among the early critics of Fechner’s approach to measuring the Psychic $\mathrm{\Psi }$ is von Kries (1882). He contends that, in reference to the Psychophysical Law established by Fechner (1860a, 1860b) that Fechner’s apparent demonstration of measuring $\mathrm{\Psi }$ on a metric scale ultimately relies on implicitly made (axiomatic) assumptions. von Kries (1882) defines the measurement process proposed by Fechner as the setting equal of the non-identical, referring to an entity ($\mathrm{\Psi }$) and its measure, which in today’s psychometric measuring approaches typically termed as $\mathit{\theta }$ .¹ In his critique of Fechner’s approach, von Kries (1882) distinguishes between theoretical and practical measurability. The former addresses the fundamental question of the existence of equalities (fundamental units) in the entity $\mathrm{\Psi }$ to be measured. From today’s perspective, it can be noted that von Kries’ criticism ultimately boils down to the problem of nomic measurement as formulated by (Chang, 1995, 2004). In other words, the theory, in Fechner’s case the assumption of the equality of sensations, falls into the domain of the measurement itself.

While Fechner focused on measuring stimulus-related sensations in psychological research, contemporary psychological and social science measurement largely centers on evaluating constructs such as personality traits, personal attitudes, cognitive abilities, political orientations, and other opinion patterns. These constructs may also encompass varying numbers of dimensions. These constructs or their single dimensions are usually assessed using questionnaires (e.g. Heine, 2020). Conceptually similar statements (items) are aggregated into psychometric scales, which are subsequently interpreted as a quantitative representation of a latent variable through scaling. The underlying concept is to regard individual items as the smallest unit of measurement (Osterlind, 1990), serving as manifest indicators of latent variables that are not directly observable in surveyed individuals (Kromrey, 1994). In empirical social science research, these latent variables represent dimensions of theoretical constructs introduced to explain the observed relationships among items, which are considered as manifest indicators (e.g., Borsboom, 2008). The primary objective is to quantify the various manifestations in the latent variables into numerical indices, thereby ostensibly measuring the corresponding trait expressions (e.g., Narens & Luce, 1986).

Now, let’s consider a slightly different definition of measurement within the framework of latent variables, contrasting it with the traditional notion of measurement as the counting of units. We will examine the classical definition of measurement provided by Stevens (1958). In the context of his definition of scale levels, Stevens (1958) states:

In its broadest sense, measurement is the business of pinning numbers on things. More specifically, it is the assignment of numbers to objects or events in accordance with a rule of some sort. (Stevens, 1958, p. 384)

While this definition appears generally comprehensive and valid from an operationalistic perspective (but see Kantor, 1938; Koch, 1992), its crucial weakness lies in the lack of specificity in the final part of the statement, particularly in the phrase “ with a rule of some sort.” Whereas Fechner for measurement of $\mathrm{\Psi }$ attempts to form a unit for mental perception and thus ultimately establishes a very specific rule for the “pinning numbers on things,” such a derivation of a specific and theoretically justified rule for questionnaire items initially remains undefined. Instead, a comparatively trivial assignment scheme is typically used during questionnaire evaluation as part of a so called “per fiat” or “bona fide” measurement: E.g., $\mathit{Yes}\Rightarrow 1;\mathit{No}\Rightarrow 0$ or $\mathit{strongly}\mathit{disagree}\Rightarrow 0$ to $\mathit{strongly}\mathit{agree}\Rightarrow 4$. The process of applying such rules, or similar ones, is commonly referred to as “scoring” (cf. Leunbach, 1961). At the core of this procedure lies the question of which scale level is implicitly assumed when assigning numbers to empirical phenomena. The definition of a specific scale level during scoring remains undetermined initially, as the verbal content of the items is first translated into a symbolic space. Subsequently, in the data analysis phase, this symbolic representation can be treated either as “numbers” or merely as “numerals” (see e.g. Uher, 2022). Thus, as Berglund et al. (2012) noted, there are two main strands of metrology in psychology, which are: psychophysics and psychometrics. Although these two metrological approaches have different foundations, both rely on the shared assumption of the metric quantifiability of $\mathrm{\Psi }$. While Fechner’s psychophysics is grounded in physics (cf. Fechner, 1858, 1860a, 1860b), psychometrics relates to the principles of social science data analysis using statistical methods.

An entertaining and classic example of the indeterminacy of the scale level of the resulting data (matrices) and the resulting confusion in the different interpretations and corresponding statistical treatments of symbolic representations as “numbers” or “numerals” can be found in Lord’s (1953) thought experiment on the statistical treatment of soccer shirt numbers of soccer players (Lord, 1953). In Lord’s (1953) thought experiment, the symbolic representation of soccer shirt “numbers” was initially intended solely for player identification, aligning with a nominal scale level. However, one soccer team interprets these symbols as “numbers” in the mathematical sense, particularly when comparing the average sizes of their numbers to those of another team. This difference in interpretation sparks a contentious debate over whether calculating the mean values of the soccer shirt numbers is appropriate to address the team’s complaint. When consulted, the imaginary statistician in Lord’s experiment responds affirmatively, dismissing the objection based on nominal scale level with the remark, “The numbers don’t know that” (Lord, 1953, p. 751). Indeed, numbers lack inherent knowledge of their intended scale. Moreover, Zand Scholten and Borsboom (2009) demonstrate in a reanalysis of the thought experiment that utilizing statistical methods assuming a metric scale level, in reference to the numerical values of the soccer shirt numbers, is indeed valid for evaluating the football team’s complaint.

Despite the elegant mathematical derivation provided by Zand Scholten and Borsboom (2009) based on the numerical values of soccer shirt numbers and the ensuing complaint by the soccer team, we believe that the purely mathematical reinterpretation of Lord’s soccer shirt numbers paradox misses the crux of the issue. One might respond pointedly in the spirit of the imagined statistician: while the numbers themselves may lack awareness, the scientific researcher should possess such insight. In other words, as noted by Uher (2022), numerals, as symbols from a symbolic universe, can encode numbers, order relations, or qualitatively different properties Uher (2022, p. 2532). This highlights the importance of understanding the symbolic context and the intended meaning behind numerical representations, and not confusing them with the research phenomena themselves (e.g. Uher, 2021a).

The example of interpreting soccer shirt numbers in Lord’s thought experiment encapsulates several key points elucidated in our preceding sections. First, the arbitrary interpretation of soccer shirt numbers highlights the fundamental question of deriving an objectively grounded scoring rule for assigning numerical values, as outlined by Stevens (1946). Secondly, the example underscores that the choice of measurement and subsequent statistical methodology hinges on the a priori perspective taken on real-world phenomena, echoing a Kantian notion. The appropriateness of interpreting soccer shirt numbers as either numbers or mere symbols rests on competing theories that offer different explanations for their significance. From a purely “soccer-centric” viewpoint, one might argue for a symbolic space merely facilitating player differentiation. Conversely, the complaint raised by the soccer team suggests a theory linking the average numerical size of shirt numbers to team reputation. In this respect, different interpretation of the data and evaluation strategies can be justified in this example, depending on the theory pursued – the “soccer-centric” or the “reputation” theory. Thirdly, in our view, the example therefore underlines the necessity for a broadly accepted agreement on a justified a priori theory in methodological and metrological considerations, a concept Chang (1995) terms “nomic measurement.” Depending on the chosen theory, measurement, and data analysis approaches diverge, as aptly summarized by the imagined statistician’s quip, “the Numbers don’t know.”

In recent years, a contentious debate has reignited regarding the measurement level of psychological dimensions (e.g., Borsboom & Mellenbergh, 2004; Kyngdon, 2008a, 2011a; Michell, 2000, 2014; Sijtsma, 2012). Fueled by the perceived solid foundation of sophisticated scaling models in Item-Response-Theory (IRT), there’s a prevailing belief that such models ensure quantitative measurement on a metric, specifically interval scale level. However, regarding the interval scale measurement by axiomatizing quantification, Lehman (1983) notes: “The axioms defining the topological or Archimedean properties are empirically untestable ‘technical’ axioms, while the other axioms, e.g., order, are testable” (Lehman, 1983, p. 511). To establish fundamental measurement in psychology and the social sciences, some authors (see e.g., Green & Rao, 1971; Narens & Luce, 1986) refer hopefully to the principle of additive conjoint measurement (cf. Luce & Tukey, 1964), specifically developed in the framework of representational measurement theory (Kyngdon, 2008b). Moreover, Irtel (1987) argued that the Rasch model, implying specifically objective comparisons being a fundamental characteristic of science as pointed out by Rasch (1977), shares some basic principles of conjoint measurement. This conjoint approach was seen as so promising that Green and Rao (1971), for example, went so far as to state that “… conjoint measurement procedures require only rank-ordered input, yet yield interval-scaled output” (Green & Rao, 1971, p. 355). However, as Trendler (2019a) notes, psychology has nevertheless not yet succeeded in fulfilling even the first condition for a quantity, namely the identification of equal perceptual magnitudes (fundamental units) in $\mathrm{\Psi }$, and thus terms conjoint measurement a “... superfluous method for the investigation of measurability of psychological factors.” (Trendler, 2019a, p. 102).

The problem with most applied representational theoretic approaches to psychological measurement lies at their core in neglecting the exploration of actual relations in empirical phenomenological (object) space $\mathrm{\Psi }$. This is also reflected in Stevens’ taxonomy of scale levels (Stevens, 1946, 1958), which is purely defined by admissible transformations in the number space. While these approaches, along with the psychometric models built upon them, offer insights into admissible transformations and mathematical properties, they fail to elucidate the empirical facts these scales are meant to represent (see e.g., Díez, 1997a, 1997b). The gap between mathematical models and empirical reality has led some critical authors to deem the use of mathematical models for psychological measurement as reasonably ineffective (cf. Schönemann, 1994). Others, such as Campbell (1921), questioned psychology’s status as a science, arguing that it lacks a coherent theory about the scale level of psychological constructs ($\mathrm{\Psi }$), distinct from their measurement ($\mathit{\theta }$). In essence, psychometric measurement approaches still suffer from a “lack of bridges between theory and data” (Cliff, 1992, p. 188). Moreover, Kyngdon (2008b) argued mathematically that the Rasch model’s conceptualization of an empirical relational structure does not encompass “empirical objects or events” (Kyngdon, 2008b, p. 100). Similarly, Kyngdon (2011a) demonstrated that the interval scale produced by the Rasch model can still align with the ordinal attributes of the underlying variable.

To conclude our reflections on attempts to quantify the psyche, we draw two interim conclusions: Firstly, spanning over a century, the efforts of scientific psychology have led to the widespread acceptance that inherently invisible (latent) attributes, such as a person’s intelligence, mathematical ability, or reading and writing skills, can be measured. Secondly, the observation of this now widespread acceptance may be viewed as evidence that, in general, relationships exist between spatial metaphors in our language and the conceptualization of abstract terms (such as $\mathrm{\Psi }$ here). More specifically, there is also an inverse relationship, suggesting that linguistic metaphors not only reflect the thoughts of speakers but also influence them, altering the way humans conceptualize abstract terms (cf. Casasanto & Bottini, 2014).

However, it remains an open question whether psychological attributes can truly be measured metrically on an interval scale, or, more fundamentally, whether they possess this interval property at all. Secondly, concerning the Kantian and current metrological distinction between extensive and intensive quantities, we align with Schönemann (1994), who suggested that “social scientists [might] have fundamental measurement, they just do not have any extensive measurement” (Schönemann, 1994, p. 153; addition in square brackets by authors).

Psychometric models and paradoxes

As outlined above, a common foundation for today’s psychometrics and measurement theory is the classification of scale levels according to Stevens (1946). Within this classification, the interval scale holds particular importance because psychological scales are often assumed to adhere to it by treating test scores $\mathit{\theta }$ constituting a measure for $\mathrm{\Psi }$ on an interval scale level (i.e., “per fiat” measurement). A commonly held viewpoint in the field of psychometrics, especially in item response theory (IRT), is that the logit scale for persons ($\mathit{\theta }$) of the Rasch model (RM; Rasch, 1960) implies an interval scale for $\mathrm{\Psi }$, with the Rasch model (Equation 8(8) $\mathit{p}\left(X_{\mathit{ij}}=x_{\mathit{ij}}|{\theta }_i;{\delta }_j\right)=\frac{{\mathit{e}}^{\left({\mathit{x}}_{\mathit{ij}}\cdot \left({\theta }_i-{\delta }_j\right)\right)}}{1+e^{\left({\theta }_i-{\delta }_j\right)}};x_{\mathit{ij}}\in \left\{0,1\right\}$(8) ) given by

(8) $\mathit{p}\left(X_{\mathit{ij}}=x_{\mathit{ij}}|{\theta }_i;{\delta }_j\right)=\frac{{\mathit{e}}^{\left({\mathit{x}}_{\mathit{ij}}\cdot \left({\theta }_i-{\delta }_j\right)\right)}}{1+e^{\left({\theta }_i-{\delta }_j\right)}};x_{\mathit{ij}}\in \left\{0,1\right\}$(8)

with ${\delta }_j$ as the item parameter (difficulty) for items $\mathit{j}=1,\dots ,\mathit{k}$ and ${\theta }_i$ as the person parameter for persons $\mathit{i}=1,\dots ,\mathit{n}$. Thus, according to Equation 8(8) $\mathit{p}\left(X_{\mathit{ij}}=x_{\mathit{ij}}|{\theta }_i;{\delta }_j\right)=\frac{{\mathit{e}}^{\left({\mathit{x}}_{\mathit{ij}}\cdot \left({\theta }_i-{\delta }_j\right)\right)}}{1+e^{\left({\theta }_i-{\delta }_j\right)}};x_{\mathit{ij}}\in \left\{0,1\right\}$(8) , multiplying the difference between ${\theta }_i$ and ${\delta }_j$ by the ($0,1$) coded observations (over $\mathit{i},\mathit{j}$) in the numerator, the probability for the occurrence of the two response categories ($x_{\mathit{ij}}\in \left\{0,1\right\}$) is modeled together as a function of the parameters ${\theta }_i$ and ${\delta }_j$.

Fischer (1995, pp. 20–21) provides a proof that $\mathit{\theta }$ and $\mathit{\delta }$ in (Equation 8(8) $\mathit{p}\left(X_{\mathit{ij}}=x_{\mathit{ij}}|{\theta }_i;{\delta }_j\right)=\frac{{\mathit{e}}^{\left({\mathit{x}}_{\mathit{ij}}\cdot \left({\theta }_i-{\delta }_j\right)\right)}}{1+e^{\left({\theta }_i-{\delta }_j\right)}};x_{\mathit{ij}}\in \left\{0,1\right\}$(8) ) are unique up to a linear transformation of the form $\mathit{a\theta }+b_1$ and $\mathit{a\delta }+b_2$ whereby $b_1$ and $b_2$ are arbitrary constants. The proof does not require the common item slope $\mathit{\beta }$ to be unity, as in the standard definition of the RM. Setting $\mathit{\beta }$ to unity would imply an even stronger measurement scale, known as the “difference scale.” This scale is characterized by an arbitrary origin but a fixed, i.e., known measurement unit, the scale factor. As Verhelst (2019) noted, in the standard definition of the RM the unit is defined by fixing the item slope parameter “...at the value of 1, but any other positive value may be chosen.” (Verhelst, 2019, p. 150; emphasis added). So, once we relax the convenient but loosely-justified assumption of unit item slopes, the scale unit is no longer fixed and any arbitrary constant $\mathit{\beta }$ ($\mathit{\beta }>0$) can be chosen.

Now recall that arbitrary origins and scale factors are properties of interval scales under admissible positive linear transformations of the general form $\mathit{x}\to \mathit{\alpha }+\mathit{\beta x}$ with $\mathit{\alpha }\in \mathbb{R}$ and $\mathit{\beta }\in \mathbb{R}$ as the arbitrary intercept $\mathit{\alpha }$ and scale parameter $\mathit{\beta }$. Hence, under the mildly relaxed but reasonable assumptions, Fischer (1995) demonstrated the interval scale property of the RM.

While this proves the interval scale property of the Rasch model, what typically goes completely unheeded is that this proof only refers to the numerical relational system (nrs) of the mathematical model, leaving its connection to the empirical relational system (ers) entirely untouched. The successful application of the Rasch model can only be justified if there is reason to believe, based on empirical evidence, that relations in an attribute of persons themselves – i.e., the empirical relational system – exhibit these interval scale properties. We doubt that such empirical evidence has been found in psychology. As Michell (2008a) put it: “If we had independent evidence that abilities were quantitative (as opposed to merely ordinal), we might be able to legitimately apply the Rasch model to measuring them …” (Michell, 2008a, p. 122)

These caveats on the interpretability of $\mathit{\theta }$ person estimates as estimates for abilities or other psychological traits $\mathrm{\Psi }$ that are said to lie on an interval scale, there still exists a pervasive belief that the mere fitting of a Rasch model necessarily implies or generates an interval scale of the underlying attribute. This is presumably due to an increasing popularity of the Rasch model during the last decades in the context of large-scale assessment studies, such as for example the Programme for International Student Assessment (PISA; e.g. OECD, 2014). Skeptical readers can ascertain the frequency of the claimed connection between the Rasch model and the interval scale, in tandem with the wishful thinking of transforming ordinal observations into interval scaled measures by conducting a Google Scholar search with the following search strings: “Rasch model” AND “interval” (around $23.600$ hits) or by searching “Rasch model” AND generate interval (around $20.000$ hits) or “Rasch model” AND generating interval (around $18.100$ hits).

This reasoning regarding the quality of the interval scale level of psychological attributes, when it solely derives from the perspective of the model, is flawed. Successfully fitting a Rasch model does neither empirically imply an interval scale of the underlying psychological entity/attribute $\mathrm{\Psi }$ nor does it generate such a scale by mapping probabilities of getting an item correct onto a continuous number line, thereby magically raising the simple counts of response categories to metric quantitative relations between objects by merely applying the Rasch model. Moreover, regarding the assertion that the fit of a Rasch model at least suggests an interval scale of the psychological attribute, Michell (2004) argues that one can successfully fit a Rasch model to data that actually satisfy only partial orders (i.e., a non-metric but ordinal structure). This is because the Rasch model’s probabilistic nature implies less demanding requirements of statistical model fit than ordinal response models, which typically use deterministic approaches to directly test order relations among objects. This was later demonstrated by Kyngdon (2011a) within a Bayesian framework for ordinal statistical inference. He transformed Rasch-fitting data from the Lexile Framework for Reading into item response proportions, testing axioms of conjoint measurement (see Karabatsos, 2001; Luce & Tukey, 1964). Cancellation axioms were supported only under specific conditions, suggesting reading ability was quantitative but the theoretical framework incomplete. As a result of the findings and theoretical considerations based on proofs by Krantz et al. (1971), Kyngdon (2011a) concluded that a notable consequence of his study is that “ Fit of an IRT model to ability test data may only be indicative of ordinal structure in human cognitive abilities” (Kyngdon, 2011a, p. 492). This aligns with earlier discussions regarding the quality of scale for psychological attributes, or more specifically, the type of “quantification” (e.g., ordinal or interval scale) of cognitive abilities proposed by Luce (2005); see also Perline et al. (1979).

In our view, the assertion that the Rasch model “generates” an interval scale stems from a misconception about measurement, which is rooted in a problem hidden in plain sight. It is crucial to remember that, echoing Pfanzagl (1959), the objective of a measurement model is solely to map an empirical set $\mathit{M}$ to a set of real numbers, enabling “conclusions concerning the relations between elements of $\mathit{M}$ [to] be drawn from the corresponding relations between their assigned numbers” (cf. Pfanzagl, 1959, p. 283; addition in square brackets by authors). In relation to such a mapping, Pfanzagl (1971) specifically distinguished between homomorphisms and isomorphisms. The latter is characterized as an invertible, unique, and bijective connection of the relations between the origin images in $\mathrm{\Re }$ (objects in an empirical relational system, ers) and the numerical relational system (nrs) in $\mathbb{R}$. In contrast, a homomorphic mapping maps the elements of one set into another set in such a way that only certain structural features of the origin images are preserved.

Recall that Rasch-scaling (e.g., by means of conditioning on score groups) typically yields the same parameter estimate $\mathit{\theta }$ for every raw-score group, that is there are several persons from the population sharing the same estimate – which in essence leads to a classification preserving only certain structural features of the classified objects. These preserved structural features of $\mathrm{\Psi }$ may relate to an ordinal or interval scale level, as both can be mapped to the interval scale level of the nrs of the Rasch (person) parameters. A point that is easy to overlook here is that in both cases the mapping of the Rasch model scale values correspond to, or rather preserve, the empirical relations between properties of objects. Roughly speaking, interval-scale properties between attributes of objects must already exist in the empirical relational system. Merely assigning real-numbered values to objects does not establish a mapping of empirical to numerical relations at all. However, in psychological measurement practice, it seems to us that there is little empirical justification or evidence that empirical relations among psychological attributes of agents/objects themselves have a relational structure on an interval scale. Instead, it appears to be a convenient or desirable assumption.

But, what is proposed and discussed under the term Rasch Paradox seems to undermine this convenient assumption. The term “Rasch Paradox” is rooted in the perspective that views the Rasch model as a probabilistic version of an additive scale, allowing for error (see Michell, 2014). From this standpoint, the paradoxical situation – in the sense of being an apparently anomalous result – arises when, if it were possible to eliminate all error factors, it would adversely affect the resulting measurement: This transformation would downgrade the scale from a metric, or specifically, interval level, to an ordinal level, as realized in the so-called Guttman “model.” This paradox is noteworthy, considering the typical assumption that an improvement in accuracy (reduction of error) always leads to a better (higher) level of measurement. However, adopting this perspective, the concept of the “Rasch Paradox” essentially arises from reasoning about the nature of error, in conjunction with the implicitly made assumption – yet to be empirically tested – of a metric nature of the psychological traits $\mathrm{\Psi }$ themselves to be measured.

The crux lies in distinguishing between Homomorphisms and Isomorphisms concerning the unresolved question of the scale level of the psychological property itself. The nature of the homomorphic mapping in Rasch scaling implies the preservation of any scale level less than or equal to the interval scale level, based on Stevens’ taxonomy (Stevens, 1946). However, the interval scale level is only guaranteed in the nrs of Rasch parameters, as demonstrated by Fischer (G. H. Fischer, 1995, pp. 20–21). As with any homomorphic mappings, the direction of the mapping, and thus the corresponding inference about scale levels, is crucial. Simply put, using a scale in a mathematical metric space suitable for representing an interval scale level does not automatically confer that scale level to the psychological trait itself mapped to such a metric space. According to Stevens’ taxonomy, any scale level less than or equal to the interval scale of an ers can be represented in a nrs for which an interval scale level has been established. From a set-theoretical perspective, the following inclusion relationship can be formulated with regard to the informative value of Stevens’ scale levels in terms of the empirical relational systems (ers) they might represent and the transferability of specific scale levels: $\mathit{Nominal}\subset \mathit{Ordinal}\subset \mathit{Intervall}\subset \mathit{Ratio}$

The relationship between scale levels, implicitly formulated in the taxonomy of Stevens (1946), can be likened to the relations between different mathematical number ranges. A number range refers to a set of numbers with common properties, typically concerning the feasibility of certain arithmetic operations within that range. Similar to the hierarchical set relations in the scale levels of Stevens (1946), there exist hierarchical relations between different number ranges. For instance, starting with the set of natural numbers $\mathbb{N}$, it is always true that number ranges defined by extending others can be conceptualized as supersets of the respective initial sets used to derive the extended number sets. Therefore, the following inclusion relations can be established: $\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}\subset \mathbb{C}$.

Once again, this does not imply that the reverse conclusion, from the eventually proven scale level of the numerical relational system (nrs) to the scale level of the empirical relational system (ers), is automatically applicable. To illustrate the importance of such a differentiated connection, or mapping, between the numerical (nrs) and the empirical numerical system (ers), let us refer to a counterexample provided by Pfanzagl (1971, p. 76), which illustrates a case where the direction of the mapping plays a decisive role in the medical decision-making process. The example provided by Pfanzagl (1971) uses a medical blood serum test to measure the intensity of certain pathological processes. The test itself relates to the extent of sedimentation in a tube after sodium citrate is added to the blood serum. The amount of sedimentation is measured on a $\mathit{mm}$-scale, “which might give the illusion of an interval scale” (Pfanzagl, 1971, p. 76). Furthermore, Pfanzagl (1971) points out that although the height of the sediment is monotonically related to the intensity of pathological processes, it is not possible, from a substantive scientific or medical perspective, to conclude that “a therapeutic agent $\mathit{A}$ which decreases the sediment from 75 to 60 [mm] is more effective than an agent $\mathit{B}$ decreasing the sediment from 65 to 55” (Pfanzagl, 1971, p. 76; addition in square brackets by authors). This conclusion is underscored by the fact that “changes in the procedure of its determination (such as changes in the amount of sodium citrate or the time interval after which the height of sediment is determined) will not at all lead to a linear transformation of the scale “ (Pfanzagl, 1971, p. 76; emphasis added). However, as we’ve exemplified in the proof provided by Fischer (1995, pp. 20–21), such a linear transformation would be a prerequisite for a relational system to be at the interval scale level. In this manner Mislevy (1987) pointed out that taking IRT models as a general solution to explain different true score distributions based on arbitrary subsets of items (on interval scale level) might be misleading (regarding the assumed interval scale level), because “this line of reasoning runs from model to data, not from data to model as must be done in practice.” (Mislevy, 1987, p. 248, emphasis added).

Along such lines of argumentation, Kyngdon (2008b) argued mathematically that the Rasch model’s relational system does “not contain empirical objects of events” (Kyngdon, 2008b, p. 100) and will then always map probabilities onto the real number line. Hence, applying the Rasch model “does not lead to a representation of properties of objects as relations between numbers but is about the creation of variables, thereby tacitly avoiding whether the psychological variable under investigation is actually quantitative” (Bond et al., 2020, p. 12). In addition, even Georg Rasch himself noted in a very nuanced way that the strong need apparent in psychology for “… replacing the original qualitative observations by measurable quantities.” should not lead to the assumption, simply by substituting quantitative parameters for the observations, that “… we have an appropriate measurement on a ratio scale or on an interval scale of individuals or stimuli or that even an appropriate order is available.” (Rasch, 1961, p. 331).

In contrast to the interval scale level supposedly formally implied by the application of the Rasch model, there are more cautious assumptions concerning the relationship between persons and items in Guttman’s “model” for dichotomously scored responses (see Guttman, 1944, 1947). This “model” was introduced under the term scalogram analysis (see Guttman, 1947) as a procedure for testing the hypothesis of cumulative, summative scalability of a set of items from “a universe of attributes² “ (see Guttman, 1944, p. 140) for a given population. Although at first described by Guttman (1947) as a pure technique for “data sorting” or to find “an adequate basis for quantifying qualitative data” (see Guttman, 1944, p. 139, emphasis added), it is typically stated, that Guttman’s cornell technique (Guttman, 1947) ultimately implies (in analogy to the Rasch model) two “model parameters” to “model” the persons’ answers to the items of a scale. In analogy to the RM these two implicitly assumed “parameters” $\mathit{\theta }$ and $\mathit{\delta }$ may be seen to represent the positions of persons and items on the latent continuum of the attribute dimension. They are connected in the Guttman “model” in a deterministic way in order to describe the occurrence of one of the two response categories. But note, that in fact Guttman (1944, 1947) never claimed his scalogramm analysis – or in his own 1947 words “... simple scoring scheme.” (cf. Guttman, 1947, p. 251) – to be a psychometric model to describe the process of persons’ responses. Rather, Guttman (1944) describes in his paper on the “basis for scaling qualitative data” a scoring procedure “...to assign to a population a set of numerical values like 3, 2, 1, 0.”, which “...will be called the person’s score.” (Guttman, 1944, p. 143). He further points out, that for example “… a score of 2 does not mean simply that the person got two questions right, but that he got two particular questions right, namely, the first and second.” (Guttman, 1944, p. 143; emphasis added). It is only in later writings on Guttman’s principle of scoring that a mathematical formal representation in the sense of a model is given, which is why we may speak (for convenience) of a Guttman “model” for the rest of the present article, although it was clearly pointed out that Guttman himself did not establish his scoring principle as a psychometric model for the response process per se. However, following Doignon et al. (1984) the general principle of Guttman's scalogram analysis may be formalized afterward as follows (see also Narens & Luce, 1986):

Suppose X stands for a set of items and A is a set of persons. In the respective “model” the two permissible “probabilities” of a correct answer $\mathit{p}=0$ and $\mathit{p}=1$ traced back to the deterministic characteristic of the resulting data can therefore be formally represented as follows (cf. Equation 9).

(9) $\left(\mathit{a},\mathit{x}\right)\in \mathit{B}\iff \mathit{f}\left(\mathit{a}\right)>\mathit{g}\left(\mathit{x}\right)$(9)

with the real numbers $⟨\mathbb{R},>⟩$ and $\mathit{f}:\mathit{A}\mapsto \mathbb{R}$ and $\mathit{g}:\mathit{X}\mapsto \mathbb{R}$; with $\mathit{B}$ as the biorder (Doignon et al., 1984), that is, sets equipped with two partial orders. Equation 9 is unique up to a positive monotonic function K for $(\mathit{f},\mathit{g})$ and $(\mathit{f}{ }^{\mathrm{\prime }},\mathit{g}{ }^{\mathrm{\prime }})$ so that

(10) $\mathit{f}{ }^{\mathrm{\prime }}=\mathit{K}\circ \mathit{f}$(10)

and

(11) $\mathit{g}{ }^{\mathrm{\prime }}=\mathit{K}\circ \mathit{g}$(11)

as an admissible transformation with ‘$\circ$’ denoting function composition as described in Ducamp and Falmagne (1969). Note, that “admissible transformation” can mean any order-preserving transformation, so that the biorder comprising the two partial orders can also be mapped for example to the order relation of the natural positive numbers ${\mathbb{N}}_{+}$, which is typically the case in applied data evaluation scenarios when the summation is formed from the $0,1$ coded item responses as a person score.

Thus, the Guttman scale defines ordinal relationships of persons and items on the latent attribute continuum, not metric ones on at least an interval scale level. The condition expressed in Equation 9(9) $\left(\mathit{a},\mathit{x}\right)\in \mathit{B}\iff \mathit{f}\left(\mathit{a}\right)>\mathit{g}\left(\mathit{x}\right)$(9) then refers to the existence of a sample- or person-invariant (ascending) order of the items according to their difficulty. Under this “model”, the marginal sums of the data matrix are sufficient (i.e., exhaustive) statistics of the two “parameters”³ $\mathit{\theta }$ for the person ability and $\mathit{\sigma }$ for the item difficulty. Based on these two formal model definitions, a taxonomy widely (however misleadingly) adopted in the field of IRT is the assignment of the Rasch model for measurement at interval scale level and the Guttman model for measurement at ordinal scale level.

In addition to the differences between the two models briefly outlined above regarding the implicitly assumed scale level, they also differ in another important characteristic. While the Rasch model explicitly takes into account a certain amount of measurement error due to its probabilistic model formulation (cf. Equation 8(8) $\mathit{p}\left(X_{\mathit{ij}}=x_{\mathit{ij}}|{\theta }_i;{\delta }_j\right)=\frac{{\mathit{e}}^{\left({\mathit{x}}_{\mathit{ij}}\cdot \left({\theta }_i-{\delta }_j\right)\right)}}{1+e^{\left({\theta }_i-{\delta }_j\right)}};x_{\mathit{ij}}\in \left\{0,1\right\}$(8) ), the Guttman “model” excludes error in the measurement due to its deterministic relation between a person’s ability and the item difficulty (see also Heine, 2020, for a detailed discussion of probabilistic and deterministic models of IRT). Regarding its probabilistic nature, Wood (1978) showed that the Rasch model even fits simulated coin-tossing data very well. Conversely, Kubinger and Draxler (2007) demonstrated that the fitting and testability of the Rasch model failed under idealized Guttman conditions in empirical data, due to a violation of the uniqueness condition for (conditional) maximum likelihood parameter estimates.

Despite their differences in specific model formulation, wherein the Guttman “model” refers to a deterministic relationship between persons and items and the Rasch model introduces a probabilistic element, both models share a fundamental common ground. This commonality lies in formalizing a dominance relationship between persons and items. While the Guttman “model” embodies this relationship deterministically (see Equation 9(9) $\left(\mathit{a},\mathit{x}\right)\in \mathit{B}\iff \mathit{f}\left(\mathit{a}\right)>\mathit{g}\left(\mathit{x}\right)$(9) ), the Rasch model adds a probabilistic component to accommodate an error element in response data. Additionally, the Rasch model provides a mathematical formulation that defines this probabilistic dominance relation as the difference between two parameters ($\mathit{\theta }-\mathit{\delta }$), thus classifying the model as parametric (see Equation 8(8) $\mathit{p}\left(X_{\mathit{ij}}=x_{\mathit{ij}}|{\theta }_i;{\delta }_j\right)=\frac{{\mathit{e}}^{\left({\mathit{x}}_{\mathit{ij}}\cdot \left({\theta }_i-{\delta }_j\right)\right)}}{1+e^{\left({\theta }_i-{\delta }_j\right)}};x_{\mathit{ij}}\in \left\{0,1\right\}$(8) ). This characteristic underpins the argument for the interval scale level of person parameters within the Rasch model, a perspective that is generally accepted in psychometrics without challenge.

Based on this, Michell (2000) provocatively diagnosed psychometric science as a pathological science, since it does not recognize the axiomatic setting of quantitative measurability of psychological traits on interval scale level as a (mere) hypothesis to be tested. Moreover, with regard to psychometric models from IRT (such as the Rasch model), Michell (2008b) concludes that they have not yet met the challenges of seriously testing the relevant hypothesis for measurement at the interval scale level (see also Heene, 2013).

In the following paragraphs, for added clarity, and because many theoretical papers have neglected to provide an illustrative example, we will demonstrate that a well-fitting Rasch model does not inherently imply anything regarding the scale level of the empirical relational system (ers). Firstly, this is based on a simple theoretical consideration regarding the common basic conceptual idea of the Rasch and Guttman scaling. Secondly, we use a random, increasing error component as an empirical basis for model testing, starting from ideal-typical simulated dominance response process data.

Simulation as illustration

Outline and rationale

Drawing on the shared concept of a dominance relation regarding items and persons between the two scaling techniques and their discrepancy regarding an error component, the simulation presented below aims to amalgamate ideal-typical dominance “response” data (Guttman “model”) with an escalating random error element, akin to complete random “response” data stemming from coin-tossing scenarios (e.g., Wood, 1978). This blending process anticipates the emergence of a dataset compliant with the Rasch model, exhibiting optimal fit for a certain degree of added error. Subsequently, Rasch model parameter estimates and model fit indices are computed based on each of the simulated datasets. Additionally, coefficients for internal consistency according to Kuder and Richardson (1937), but see also Cronbach (1951), as well as (Rasch) residuals (cf. Wright & Masters, 1982) derived from IRT scaling are evaluated.

All data simulation and analyses were performed using the statistical environment R (R Core Team, 2023) and the current versions of the CRAN published R-packages Hmisc, pairwise, CTT, ggplot, future.apply (see Bengtsson, 2021; Harrell, 2023; Heine, 2023; Wickham, 2016; Willse, 2018, respectively) as well as a yet not on CRAN published R-package named pattern providing convenient functions for data simulation. All materials necessary for replicating the analysis presented in this paper, including the R-code, the package pattern, and the simulated datasets, are provided on OSF at the following link: https://doi.org/10.17605/OSF.IO/GQVHC.

Simulated datasets and parameter estimation

Starting from perfect Guttman data comprising $\mathit{n}=1000$ rows (persons) and $\mathit{k}=10$ columns (items) we contaminated this perfect data in increments of 5% (ranging from 5% to 100%) with a random error component. For each of these data generating steps, $\mathit{r}=100$ replications were created. Item and person parameters were sampled from a standard normal distribution $\mathit{N}(0,1)$. For each of the resulting 2000 data matrices ($20$ steps $\times 100$ replications), the parameters of the Rasch model parameters were determined with the package pairwise (Heine, 2023). From the results, the likelihood ratio ${\chi }^2$-values of the Anderson model test (cf. Andersen, 1973) and the corresponding p-values were calculated. Furthermore, the squared score residuals (cf. Wright & Masters, 1982), averaged over persons and items, were determined. In addition, classical test theory internal consistencies of $\mathit{KR}\text{-}20$ statistic according to Kuder and Richardson (1937) were calculated. The individual values for the respective coefficients are plotted on graphs, with the x-axis representing increasing levels of mixing between the Guttman data and random response data (error component).

Results

Figures 1–4 display the values of various coefficients obtained from fitting the Rasch model, plotted on the y-axis. The x-axis represents the percentage (in 20 levels) of contamination of the pristine Guttman data with an increasing proportion of random error. The scale endpoints of the x-axis correspond to perfect Guttman data, located on the left side of each figure, and completely random data, located on the right side of each figure.

Figure 1. Distributions of ${\chi }^2$-values of Andersen Likelihood-Ratio-Test (cf. Andersen, 1973) by percent random contamination of Guttman response data with 100 replications each; diamond shaped dots represent means across replications respectively.

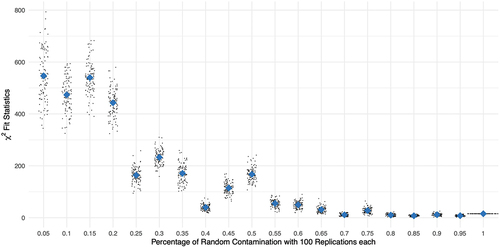
Figure 2. $\mathit{p}$–values of Andersen test (cf. Andersen, 1973) by percent random contamination of Guttman response data with 100 replications each; diamond shaped dots represent means across replications, respectively.

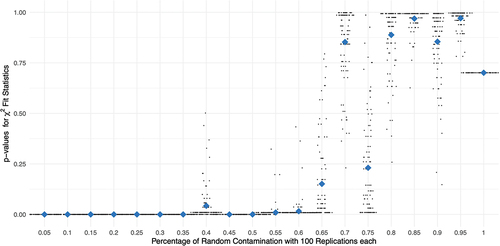
Figure 3. Mean values of squared score residuals across persons and items by percentage random contamination of Guttman response data with 100 replications each; diamond-shaped dots represent means across replications, respectively.

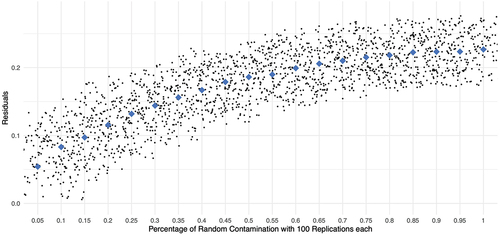
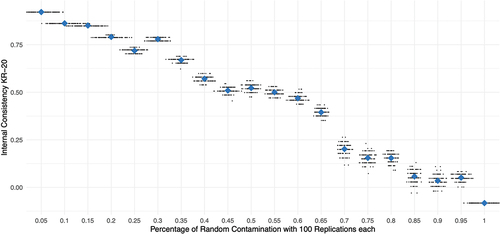
Figure 4. Values of Kuder-Richardson 20 ($\mathit{KR}\text{-}20$) as measure of test reliability (cf. Kuder & Richardson, 1937) by percent random contamination of Guttman response data with 100 replications each; diamond-shaped dots represent means across replications.

Figure 1 illustrates the trend in the ${\chi }^2$-fit statistics of the Andersen Likelihood Ratio Test (LR-Test; cf. Andersen, 1973) across the simulated data matrices (x-axis). The graph shows a decreasing trend in the values of the ${\chi }^2$-fit statistics, with the lowest value observed for the completely random data on the right-hand side of Figure 1.

In line with the decreasing trend observed in the ${\chi }^2$-test statistics (Figure 1), the corresponding $\mathit{p}$-values depicted in Figure 2 indicate significant model misfit in datasets with low percentages of random error contamination. Specifically, datasets with up to approximately 35% random error suggest a misfitting Rasch model. Paradoxically, datasets with a relatively high proportion of error, starting at around 65%, appear to exhibit a perfect model fit, as evidenced by insignificant $\mathit{p}$-values (see Figure 2).

Figure 3 illustrates the progression of means across persons and items of the squared score residuals (y-axis) across simulated data matrices (x-axis). Unlike the descending trend observed in the ${\chi }^2$-statistic and the apparent improvement in model fit following the LR-test (as indicated by the trend in the $\mathit{p}$-values in Figure 1), which coincides with an increasing proportion of error in the Guttman data, the progression of score residual values (as seen in Figure 3) “accurately” reflects that the increasing proportion of error is accompanied by a growing “discrepancy” between the assumed dominance relation between persons and items in the model and the actual data. A skeptical and attentive reader might argue that these deviations indicate discrepancies between the Rasch model and the actual ordinal data structure. However, this is incorrect. The residual statistic merely reflects the deviation of observed responses from predicted probabilities under the Rasch model, as empirical response functions become increasingly shallow compared to those under the Rasch model with a higher amount of random error. Thus, the residual statistics quantify deviations from the expected Rasch model probabilities, not deviations from the actual ordinal structure of the ers!

Figure 4 illustrates the progression of coefficients of the $\mathit{KR}\text{-}20$ internal consistency statistic according to Kuder and Richardson (1937). Interestingly, and in contrast to the trend observed in the $\mathit{p}$-values of the LR test, the decreasing trend in the $\mathit{KR}\text{-}20$ statistic effectively indicates the increasing noisiness of the data due to the growing random error component (see Figure 4).

As we can see, the addition of more random error actually improved the fit of the Rasch model, despite the fact that the actual scale of the ers was only ordinal. This highlights that successfully fitting a Rasch model by itself provides no information about the scale level of the ers, nor does it therefore imply a successful mapping, i.e., measurement. The simulation also illustrates the point made by Kyngdon (2011a) that the “interval scales” created by item response models are consistent with nothing more than ordinal attributes of a trait. It is important to remember that these “scales” are not composed of units of something real; they are just real numbers generated from data with a logistic test model under certain constraints.

Outlook to possible new research strand on interpreting quantitative statements

Given that contemporary psychological measurement frequently involves assessing concepts and constructs via questionnaires, self-assessments, or peer evaluations, it appears almost self-evident that these methods predominantly utilize language as a key medium of human communication. Whether conveyed in written form through questions (item stimuli) or orally in standardized interviews, language is critical. This reliance on language is especially pronounced in areas such as individual differences and personality psychology, which examine variations in human traits between individuals. Constructs such as personality and self-confidence are commonly measured using methods that employ language as a crucial means of expression.

For instance, the theoretical basis of the trait paradigm in personality psychology is based on the idea of analyzing human language as a methodological approach to the psychological construct of personality (cf. Baumgarten, 1933; Galton, 1884; Klages, 1926). This research approach is founded on what is known as the sedimentation hypothesis, according to which person-describing adjectives are regarded as linguistic “sediments” of real human trait differences (e.g. John et al., 1988). On the basis of this theoretical foundation, Allport and Odbert (1936) carried out one of the first psycholexical studies.

In analogy to this language-based research approach, which has proven to be somewhat fruitful in the field of personality psychology with the foundation of the Big-Five paradigm (cf. Costa & McCrae, 1985, 1992; McCrae & Costa, 1985, 1987), we would like to further substantiate our thesis that analyzing linguistic expressions can be particularly fruitful for appropriately interpreting the nuanced meanings of statements regarding psychological characteristics $\mathrm{\Psi }$.

Contrary to interpreting mental properties on an interval scale, mere ordinal quantification of abstract terms or concepts, including $\mathrm{\Psi }$, can be supported by a systematic study of human language (see Fortis, 2020; Lakoff & Johnson, 1980; Sternberg, 1990). Specifically Fortis (2020) describes the development of the linguistic concept of localism, dealing with spatial metaphors in language. Localism is the hypothesis, represented in a subfield of linguistics, that spatial relationships play a fundamental role in the semantics of languages, the history of which also goes back to Aristotle’s physics. Similarly, Lakoff and Johnson (1980) argue that an ordinal quantifying perspective on psychological properties $\mathrm{\Psi }$ can be substantiated using spatial metaphors commonly found in everyday language (termed: orientation metaphors, cf. Lakoff & Johnson, 1980).

In his book “Mappings in thought and language” on the construction of meaning when people think, act or communicate, Fauconnier (1994) generally emphasizes the importance of cognitive linguistics. Moreover, Fauconnier (1994) argues that the construction of mappings between different phenomenological domains, yet in analogy to mapping functions in the most general mathematical sense of establishing a correspondence between two sets, is the core of a uniquely human cognitive ability to produce meaning. Such cognitive processes of constructing analogies, mental mapping functions and meaning in general are subsequently reflected in linguistic utterances in the form of metaphors (see Fauconnier, 1994). In a similar vein (Lakoff & Nunez, 2009), argue for the elementary importance of linguistic metaphors in the construction of mathematical ideas and concepts. Nedelcea et al. (2012) apply this standard linguistic hypothesis to the use of metaphorical expressions in spoken language to construct meaning. They employ this approach in their studies on developing inventories for assessing anxiety and dimensions of personality through metaphorical expressions. Nedelcea et al. (2012) conclude that the findings from the psychometric review suggest that metaphorical expressions can be used to describe personality traits and to formulate items for personality assessment instruments. In addition, Sternberg (1990) in his work “Metaphors of mind”, discusses and argues for the relevance of linguistic metaphors for the definition of the concept of intelligence.

Specifically, Lakoff and Johnson (1980) point out that, in general, gradual statements about the characteristics of objects – whether interval or ordinal – refer to spatial metaphors in human language. Such metaphors arise simply from our perceived reality that as humans we have bodies that we perceive as located in a three-dimensional space. This view parallels the thesis already formulated by Kant in his Anticipations of Perception, that it is the specificity of our perceptual apparatus that determines our reality a priori. In the same way, albeit only in the form of a brief mention, Pfanzagl (1971, pp. 16–17) points to the importance of language for the dimensional representation of attributes within the framework of the representation theory of measurement.

To provide a concrete example, we can turn to Lakoff and Johnson (1980), who, in the field of clinical psychology, examines the assessment and verbal depiction of the degree of depressive mood using linguistic spatial metaphors. For example, phrases like “I’m feeling down,” “I’m depressed,” or “He’s really low these days,” as well as expressions such as “I fell into a depression.” Furthermore (see Lakoff & Johnson, 1980, p. 22), notes that “Drooping posture typically goes along with sadness and depression, erect posture with a positive emotional state.” (see Lakoff & Johnson, 1980, p. 23). Even in strictly scientific disciplines such as physics, the significance of linguistic spatial metaphors in evaluating and interpreting the meaning of quantities becomes apparent. For example, Lakoff and Johnson (1980) formulates this particularly with reference to rather abstract measurement concepts: “So-called purely intellectual concepts, e.g., the concepts in a scientific theory, are often, perhaps always, based on metaphors that have a physical and/or cultural basis. The high in ‘high-energy particles’ is based on more is up” (Lakoff & Johnson, 1980, p. 24).

Discussion

Drawing upon the theoretical explanations compiled in this article, which have been further illustrated by a small simulation, we draw several conclusions. These conclusions address various issues for practice, inference based on data, and provide recommendations for further lines of psychological research.

Regarding the simulation results, the critical insight is not that introducing error enhances the fit of the Rasch model. Instead, it is that the introduction of random error can falsely suggest that the measure ($\mathit{\theta }$) for $\mathrm{\Psi }$ is interval-scaled, even though its empirical relational system is only ordinal. This misconception is amplified as the random error in the data increases, leading to a paradoxical or anomalous outcome. In light of our simulation results, and considering that Guttman (1944, 1947) did not propose a psychological model for response processes, as illustrated by his use of the term ‘Cornell technique’ for data sorting, and following Kyngdon’s (2011a) argument regarding the lack of a behavioral theory for the scientific measurement of cognitive ability, we assert the need to make a clear distinction between two basic entities – namely, $\mathit{\theta }$ and $\mathrm{\Psi }$.

Thus, there is a critical need for psychological models to develop a more sophisticated theory concerning the response processes involved in perceiving and answering test items. This imperative must be complemented by robust empirical approaches to test the hypothesis of the interval scale level of psychological characteristics themselves, using observational data. But see Trendler (2019a) for a skeptical view whether this can ever be achieved in light of, among other things, “…limits set by nature to experimental manipulability.” (Trendler, 2019a, p. 108) and the inability “... to capture psychological processes in experimental apparatus, devices, or machines as would be required in order to control systematic disturbances.” (Trendler, 2019a, p. 120). In conclusion, it can be said that the application of the Rasch model to pure data matrices is mostly possible, but the interval-scaled interpretation is only justified if there is evidence that the empirical relationship system corresponds to an interval scale. This does not, of course, discredit the Rasch model itself but rather the blind application of it as a “cargo cult” (Feynman, 1974) where no planes land, despite its seemingly perfect form; that is, coupled with the hope that the Rasch model would seemingly be able to provide (“generate”) an interval scale for $\mathrm{\Psi }$. In a similar vein, such blind application of psychometric models may coincide with the optimism of “psychometric-natives” in their attempt to bridge the gap toward interval-scaled measurement of $\mathrm{\Psi }$. Nevertheless, as elaborated earlier and consistent with Kyngdon’s (2011a) reasoning, interval-scaled measures of $\mathit{\theta }$ can still reflect ordinal attributes of $\mathrm{\Psi }$. For further elaboration on this point, one may also refer to Bond et al., (2020, p. 270). Since simply using Rasch scaling can run the risk of succumbing to the illusion of interval scaling in $\mathrm{\Psi }$, one way to avoid this pitfall is to exercise caution when interpreting the scale level of $\mathrm{\Psi }$. Alternatively, models can also be used that from the outset only imply an ordinal scale level for both $\mathit{\theta }$ and $\mathrm{\Psi }$, such as the ordinal probability models proposed by Scheiblechner (1995, 2003).

In line with this proposed sharp distinction between $\mathit{\theta }$ and $\mathrm{\Psi }$, we can observe a clear demarcation advocated by Guttman (1944) between models for prediction, where a (latent) variable predicts individual attributes (items), and models for scaling, which, according to Guttman (1944), aim to classify and “reproduce” individual attributes (items) from a “quantitative” variable (meaning here a quantifying, at least ordinal, statement). Guttman (1944, p. 149) criticized the “…misleading character… “ of classic item analysis for scaling as “…an unfortunate carry-over from the problem of ordinary prediction of an outside variable” (Guttman, 1944, p. 149).

The authors of this paper are cognizant that the issues raised here may challenge the well-established and widely accepted understanding in the field of psychometrics, or even more broadly, the prevailing concept of psychological measurement itself – specifically, the notion of a so-called “metric” interval-scaled latent variable. In this context, the general concept of a “real metric” when operationalizing perceived mental characteristics through tests containing various items seems highly implausible to us. This skepticism arises particularly considering that Fechner (1801–1887) himself formulated the well-known “Weber – Fechner law of perception”, indicating that metric relations within a physical, scientific system (such as weight or sound intensity) do not translate into linear metric relations within subjective perception (e.g., Fechner, 1860a, 1860b). Moreover, Fechner acknowledged in his initial essay Fechner (1858) on his project to quantify $\mathrm{\Psi }$ that attempting a direct measurement would likely be futile. He noted, “… to carry out such a count directly” [… eine solche Zählung direkt vorzunehmen] since it must be acknowledged that “sensation does not divide itself into equal degrees or degrees that we could count.” [Die Empfindung theilt sich nicht in gleiche Zolle oder Grade ab, die wir zählen könnten.] (Fechner, 1858, p. 2; German spellings as in the original).

Furthermore, as a clear recommendation for future research, we argue that the question of the scale quality of psychological attributes, as per Stevens (1946, – ordinal – interval – ratio), should be explored more within the context of psychological research rather than solely within the field of psychometric modeling. To address this, making a clear distinction between psychological models for response processes, along with a theory regarding the scale quality of the respective psychological attribute $\mathrm{\Psi }$, and those models for data analysis should, from our perspective, help resolve the paradox of implicitly accepting the Rasch model while explicitly rejecting it during data analysis.

The scientific ideal of quantification aligns the quantitative aspect with the structural content of a substantive theory. In scientific psychology, especially within psychometrics, numerous models have emerged to facilitate the quantification of psychological phenomena. However, statistical models alone cannot substitute for substantive theories; detached from these, they cannot effectively contribute to the quantification of $\mathrm{\Psi }$. In a loose reference to a quote by Schönemann (1981), focusing solely on the properties of the numerical relational system of measurement just because it’s easier to control, “is like searching for a lost dime under a lamppost just because the light is better there” (Schönemann, 1981, p. 350). What appears as quantitative by the use of numbers in the Rasch model is nothing more than the reflections of the qualitative or rather ordinal relations between objects. In this respect, this perspective offers an opportunity for re-framing the traditional dichotomy of quality and quantity, already noticed in the Aristotelian times.

Given this line of argument, psychology – as a discipline increasingly quantified akin to the natural sciences – must confront a crucial question, as articulated by Max Weber (1919): Which real-world problems (“worth knowing”) within social science are effectively addressed by attempting to apply quantitative metric measures to psychological attributes? In the natural sciences, such as physics, the adoption of quantitative measures has led to significant technological advancements benefiting society, including the invention of the thermometer, the steam engine, electric lighting, lunar exploration, and the harnessing of atomic energy, all based on principles that might be considered axiomatic in a scientific-theoretical context. However, the applicability and utility of assuming the existence of metric variables in psychology as a default remain subjects of ongoing debate and inquiry. For a comprehensive overview and a comprehensible discussion of many of these issues, see Ballou (2009).

Another important point to consider is the clear distinction between samples versus populations, and specific tests with concrete items versus universes of indicators for single attributes $\mathrm{\Psi }$, as consistently emphasized, for example, by Guttman (1944, 1947). This distinction can also elucidate the significant difference between models and techniques for scaling data matrices on the one hand, and the inferences drawn from them to the populations (persons and items) on the other. Therefore, the crucial difference lies in the kind of inference drawn from test data. Regarding the latter point of different inferences from data matrices, an example that vividly illustrates this is Lord’s thought experiment on the diverse background-theory-dependent interpretation and subsequent statistical handling of football shirt numbers.

To perhaps clarify the point regarding the necessary distinction between samples and populations, as quoted by Guttman (1944, 1947), let us hypothetically assume, for example, that we have a closed and mathematically exhaustive set of “yes – no” questions on any given topic. In this scenario, the present set could not be considered as a random sample from a universe of possible questions; rather, it would be considered a complete and exhaustive set out of the sample space. The evaluation of a resulting data matrix (yes $\Rightarrow$ 1, no $\Rightarrow$ 0) and the resulting scores according to the Guttman technique could actually under the given, but certainly unrealistic conditions be interpreted on an interval scale level – depending on epistemological rigor, even at an absolute scale level. Salzberger (2010) argued similarly that “Given that the raw score is a count, its scale level is the highest possible, that is absolute” (Salzberger, 2010, p. 1274). Two points, however, which arise from the admittedly quite unrealistic hypothetical assumptions, are central to the justification of such an interpretation. First, since it would be an exhaustive set of all possible questions, this would automatically provide an absolute point zero – that is no question (of all possible ones) would be answered with “yes.” Secondly, under these conditions one could argue more plausibly that the single questions are indeed the smallest unit of measurement of the whole inventory in the sense of Osterlind’s (1990) item definition. For the latter, however, it would still have to be shown that each of these units (each single item) has an equal weight in the sense of magnitudes of equal quantity that would constitute a metric.

Rather than engaging in endless discussions of Rasch paradoxes and other paradoxes in psychometrics, it would be prudent to first focus on the concept of psychological quantity and concentrate on substantive questions, such as whether (1) there are a priori objections to theory-based quantification of the psyche, and (2) whether theory development in psychology has indeed led to the establishment of independent fundamental scales. To put it perhaps a bit bluntly, one could also frame it as follows, drawing from typical everyday experiences in verbal exchanges with others: Verbal expressions with ratio-scaled implications, such as “I am twice as self-confident as everyone else,” are, at least colloquially, often associated with attributes like exaggeration and boasting – and rightfully so, in our opinion. With reference to this common understanding of such statements, one might assert somewhat boldly that the thoughtless and unreflective application and interpretation of real-valued parameters from psychometric models as evidence for the ratio- or interval-scaled nature of $\mathrm{\Psi }$ also amounts to a form of scientific boasting.

Certainly, we do not intend to suggest that there is no gradual or quantitative difference in any mental attributes. Such a claim would be absurd, as even a cursory examination of human language usage reveals that such gradual comparisons, akin to ordinal scale level comparisons, are both common and can be practical and beneficial from a pragmatic standpoint. In the spirit of Max Weber, they indeed represent facts “worth knowing.” However, it remains to be determined to what extent statements like “Moritz is twice as clever as Jörg” or “yesterday it was twice as hot as today” hold meaning, and whether such assertions could withstand scrutiny from a substantive scientific perspective. Instead of unquestioningly accepting such or similar statements regarding $\mathrm{\Psi }$, which may be derived from the ostensibly justified interpretation of $\mathit{\theta }$ measured values from psychometric scaling models, we advocate for new psychological (rather than psychometric) research approaches. These approaches should focus on the empirical relative rather than the numerical relative, just to employ the terminology of representational theory of psychological measurement.

As we highlighted in the preceding section, it could prove highly fruitful to leverage human language as a foundation in this endeavor. Language-based approaches, such as the psycholexical paradigm, have historically yielded substantiated and insightful psychological findings, particularly within the domain of personality psychology – exemplified by the Big Five within the trait paradigm of personality.

Such attempts might successfully start from the point of psychological research were Fechner ended his line of research attempting to find meaningfully units of $\mathrm{\Psi }$.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Notes

1. von Kries means here the setting equal of an entity and its measure according to the classical dichotomy based on the Greek philosophers and mathematicians Eudoxus and Euclid. According to this, the distinction between the psychic entity ($\mathrm{\Psi }$) and its measure ($\mathit{\theta }$) can be traced back to the works of ancient Greek philosophers and mathematicians, in particular to Eudoxus of Knidos (ca. 350 BC) and his work Theory of Proportion. According to tradition, Euclid (ca. 300 BC) also laid the foundation for this distinction between concept/unit (lógos) and proportion (analogía) with his fifth book of elements.

2. Note that Guttman used the terms attribute and item in a way as synonymous in his 1944 and 1947 writings.

3. Note that Guttman never speaks of parameters in his writings on the scaling technique he proposes, nor does he term his technique model. This terminology (with the notation $\mathit{\theta }$ and $\mathit{\sigma }$) is only introduced here to make the commonality and analogy to the Rasch model understandable, which is that a dominance relation between persons and items is assumed.