Risk analysis for urban excavation: a FAHP-VIKOR hybrid method

Abstract

The construction of urban excavation involves several potential risks, and the application of scientific methodologies is necessary for a reliable risk assessment. This paper proposes a novel risk assessment framework for urban excavation that combines the fuzzy analytic hierarchy process (FAHP) with the multi criteria compromise solution ranking (VIKOR) approach. FAHP is utilised to determine the weights of risk factors and identify high risk factors, and VIKOR is employed to evaluate the risk level of urban excavation. The proposed method comprises five key components: information source collection, risk-factor rating, weight calculation, establishment of project classification standards, and project feedback. By comprehensively considering the weights of various evaluation indicators and the superiority or inferiority of different factors, this method provides comprehensive risk assessment results. The effectiveness and feasibility of the proposed method are validated through a real case conducted in Nanning, China. The FAHP-VIKOR risk assessment method offers scientific decision support for urban excavation construction and serves as a valuable reference for risk reduction and ensuring construction safety.

Graphical Abstract

Keywords:

• Excavation construction
• FAHP-VIKOR method
• risk assessment
• high risk identification
• safety management

1. Introduction

With the rapid urbanisation in China, construction has been expanding both vertically and underground, leading to an increasing number of deep basement projects, including subway stations, urban utility tunnels, and residential buildings (Ji et al. 2021; Peng et al. 2023; Shen 2023). However, the increase in the number of underground structures creates a range of hazards and risks (Lyu et al. 2022). First, the excavation can potentially damage and settle surrounding land, posing a threat to nearby buildings (Shen et al. 2023; Wu et al. 2023). These risks include slope failure, uplift within pits (Zhao et al. 2023), quicksand formation, and water seepage. Between 2020 and 2021, five incidents of excavation collapse occurred, resulting in severe casualties (Shenyang District Emergency Management Bureau (SDEMB), 2020; Yancheng District Emergency Management Bureau (YDEMB), 2021; Xiangxi Autonomous Prefecture Emergency Management Bureau (XAPEMB) 2022; Linping District Emergency Management Bureau (LDEMB) 2021; Baiyun District Emergency Management Bureau (BDEMB), 2022), as indicated in Table 1. Guo et al. (2019, 2023) conducted in-depth research on the specific difficulties of excavation and made some achievements. Furthermore, the excavation generates significant environmental pollution in the form of soil excavation, dust, noise, and various other pollutants, which adversely affect the living conditions of nearby residents and compromise their quality of life (Dagliya et al. 2023; Mai et al. 2023; Naeem et al. 2023). Hence, researchers have made strides in addressing the significant risks and hazards of excavation through various approaches, including innovative methods (Asare et al. 2023; Li et al. 2023; Hoy et al. 2023), problem-solving (Khatri et al. 2023), and material advancements (Senanayake et al. 2023; Shanban and Daef, 2023), proposing numerous targeted strategies. In general, excavation projects are associated with high risk, and the occurrence of accidents poses a severe threat to the safety of both society and residents, making it crucial to ensure safe construction (Zhang and Ji 2022; Chai and Wu 2023).

Table 1. Accident cases of foundation pit collapse from 2020 to 2021.

Date	Event	Cause	Casualty
June 3, 2020	Foundation pit collapse in Shenbei New District, Shenyang City, Liaoning Province.	Failure to take the required support and protection measures during slope excavation or for side walls	4 deaths
June 4, 2021	Foundation pit collapse in Yannan high tech Zone.	Failure to take effective safety measures, such as slope protection, to prevent collapse	1 death
August 5, 2021	Foundation pit collapse in Xiangxi high tech Zone, Hunan Province.	The construction site was buried due to landslides, falling mud and sand	4 deaths and 7 minor injuries
October 2, 2021	Foundation pit collapse in Linping District, Hangzhou City, Zhejiang Province.	Failure to implement the special construction plan	2 deaths
December 3, 2021	Foundation pit collapse in Nanhu watershed, Guangzhou, Guangdong Province.	The soil was soft and no supporting measures were adopted	1 death

Extensive research has been conducted on assessing and managing engineering risks. For example, artificial intelligence methods have been applied to excavation and tunnel construction (Shen, Elbaz et al. 2022; Shen, Zhang et al. 2022; Yan, Shen, Zhou et al. 2022; Awad et al. 2023; Qin et al. 2023; Shaban et al. 2023; Yao and Song 2023; Wang et al. 2024). Specifically, Shi, Wang et al. (2023) and Shi, Jin et al. (2023) proposed a data-driven multi-stage sampling strategy for a three-dimensional geological domain, and achieved automatic numerical simulation of large excavation. Additionally, in the domain of urban water management, analogous evaluation methods offer valuable insights and lessons for risk assessment practices (Saikia et al. 2022; Yan, Shen, and Zhou 2022; Zeng et al. 2023; Zhou et al. 2023). Multi-criteria decision-making (MCDM) methods are widely used in risk assessment because of their ability to comprehensively consider multiple evaluation criteria and establish a robust basis for decision-making processes. For instance, Lin et al. (2021) employed an improved technique for order preference by similarity to ideal solution (TOPSIS) method to evaluate the environment of concrete mixing plants comprehensively. Lyu, Shen et al. (2020) conducted a risk assessment of land subsidence infrastructure in megacities based on an improved trapezoidal fuzzy analytic hierarchy process (FAHP) method.

In excavation engineering, MCDM offers a systematic and comprehensive analytical framework for evaluating different risk factors. In reference to Lyu et al. (2023), this study collected 391 articles using the keywords “MCDM and engineering” and “Risk assessment”. A correlation analysis was conducted using the VOSviewer software, resulting in 92 keywords with a repetition frequency of 15 or more. These keywords were further filtered to generate clusters, as illustrated in Figure 1a. Cluster 1 shows analytic hierarchy process (AHP), FAHP, TOPSIS, analytical network process (ANP), multi criteria compromise solution ranking (VIKOR) and other analysis methods for MCDM. Cluster 2 shows the primary content of risk assessment in engineering, which involves identifying potential risk factors through comprehensive project analysis and discussions. It aims to ensure the safety and effectiveness of project (Wang et al. 2022; Carpio et al. 2023), prevent engineering accidents (Stankovic et al. 2020; He and Atangana Njock, 2023), and improve engineering methods (Vrtagic et al. 2021). Figure 1b depicts the timeline of the selected keywords, reflecting research trends in the field of MCDM methods. As shown in Figure 1b, the FAHP and TOPSIS are early research methods, but still hold significant research value. Researchers such as Chen et al. (2022), Lin et al. (2023a, b), Zhang et al. (2023), and Lyu, Sun et al. (2020) have continuously optimised the FAHP and TOPSIS methods by utilising combinations of various approaches to achieve more accurate risk assessments. Moreover, the utilisation of the VIKOR and geographic information science (GIS) methods emerged in the research landscape only in 2021, making them relatively new active areas of research. For example, Atangana Njock et al. (2022) used the VIKOR method to assess river pollution risk.

Figure 1. Keyword co-occurrence knowledge graph: (a) multi-criteria decision-making (MCDM) method correlation diagram; (b) MCDM research heat map for 2019–2021.

Although significant research achievements have been made in applying MCDM for risk assessment in the engineering field, there are still some limitations to the current research on risk assessment for excavation projects. First, acquiring the necessary data for risk assessment in excavation projects can be challenging because of the lack of sufficient field measurements and reliable statistical information, which restricts the establishment and validation of assessment models. Second, foundation-pit projects involve numerous complex risk factors, some of which are difficult to quantify, such as geological conditions and construction techniques, and require the exploration of suitable assessment methods. Furthermore, the treatment of uncertainty in excavation project risk assessment has not received sufficient attention and requires further improvements in methods and techniques. Finally, the current research primarily focuses on specific methods or models within the MCDM approach, and it lacks a comprehensive evaluation framework and methods that adequately consider the multifaceted risk factors associated with excavation projects.

Considering these limitations, there is a need to develop a systematic and procedural approach for the risk assessment of excavation projects that fully considers the various risk factors involved. This study proposes a novel framework that integrates the FAHP and VIKOR methods to assess and manage the risks of excavation projects in urban areas. The model establishes a hierarchical structure employing the AHP, incorporates fuzzy theory to capture the uncertainty of expert opinions, and calculates the weights of risk factors to enhance objectivity. The VIKOR method is then used to rank the risk factors, determine risk levels, and provide rational risk assessment and management strategies based on the identified risk levels. The framework can identify the high risk factors and construction risk levels, give early warning to managers, and eliminate the potential hazards in the project in time. The validity and efficacy of the proposed framework are further demonstrated through a foundation-pit case study conducted at Nanning.

2. Methodology

2.1. Framework of risk assessment and management

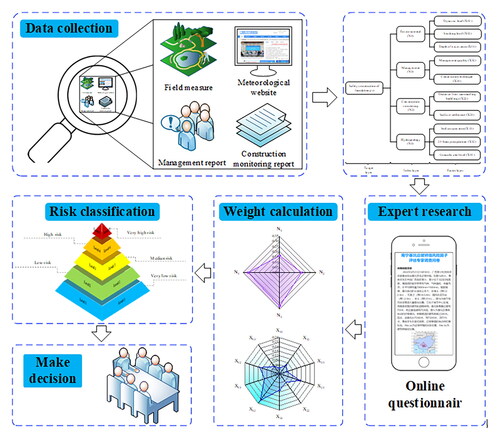
In engineering, risk assessment involves a comprehensive analysis of the potential impacts of various risk factors on engineering projects, whereas risk management entails formulating specific strategies based on the analysis results. To determine the high risk factors in engineering and ensure the accuracy of calculation, a systematic and structured risk assessment framework is indispensable. In this study, a risk assessment and management model for excavation engineering during the construction process was proposed, as illustrated in Figure 2. The model combines FAHP and VIKOR methods. VIKOR method identifies the feasible solution that is closest to the optimal solution between positive and negative ideal solutions. Essential to this process is the evaluation of proximity between each alternative scheme and the ideal solution, which is influenced by the weight of risk factors in this study. Consequently, the FAHP method is incorporated to determine the factor weights. FAHP method employs triangular fuzzy number to compute expert opinions with the consideration of both uncertainty and inconsistency. The key steps of the model are as follows.

Figure 2. Excavation risk assessment and management framework.

1. Identify risk factors: Identify the risk factors in the project through the assessment criteria, technical specifications, and technical standards of specific projects. It is necessary to collect and analyse on-site data of actual projects and processes. For instance, in excavation engineering, data can be collected from aspects such as hydrogeology, excavation design, structural considerations, management practices, and the surrounding environment to determine the influencing risk factors.

2. Establish an evaluation system: Collect normative standards for the impact factors and perform systematic quantification for them according to the standards. In instances where clear normative standards are absent, expert opinions from the relevant field can be employed to assign and quantify these impact factors. Table 2 presents the risk definitions for the hierarchical classification.

3. Calculate factor weights: Construct the decision-making hierarchy and use the FAHP to obtain the weights of the impact factors from experts in excavation, tunnelling, and geotechnical engineering. Determine high risk factors based on these weights.

4. Classify the standard and identify high risk factors: Combined with the weight of risk factors, the VIKOR method is used to calculate the quantitative standard of risk grade and identify the high risk factors.

5. Results and feedback: Assess the risk level of the excavation and make appropriate decisions. If the excavation is at a high risk level, the necessary mitigation measures, strengthening of monitoring, and adjustments to the construction plan should be implemented to reduce the risk. However, if the risk level of the excavation is low, the construction can proceed as planned.

Table 2. Risk level implication.

Risk level	LV1	LV2	LV3	LV4	LV5
Assessment	Very low risk	Low risk	Median risk	High risk	Very high risk

2.2. Weight of risk factors via FAHP

2.2.1. Decision hierarchy and fuzzy judgment matrix

In the FAHP method, the decision hierarchy is divided into three parts: target, index, and factor layers. The primary role of the factor level is to link the target and index levels, further refining and improving the decision-making process by considering the influence of different factors on the goal. In the factor level, the consideration of risk factors can help decision makers comprehensively evaluate the feasibility and potential risks of each criterion. The target and indicator layers are determined by decision-makers, and the factor layer is identified by risk factors.

In constructing the evaluation matrix, the expert system analysis method of “1–9 scale” (Lyu et al. 2019) was adopted. The questionnaire quantifies the degree of influence of each factor on the target layer as 1–9, where 1 indicates that the importance degree of the factor is equal to the importance degree of other factors, and importance degrees 2–9 indicate that the importance degree of the factor is more important than other factors. The importance increases as the number of participants grows. Notably, the advantage of this scale is its ability to maximize differentiation between factors, ensuring heightened accuracy in the results. Experts are guided to select only one score from “1 to 9” for each factor within an indicator layer. To ensure the validity of the score, factors could not be filled with the same score in the same layer.

In contrast to the traditional AHP, this study used the triangular fuzzy number proposed by Lyu et al. (2019) to replace the result value of the traditional pair comparison, which can comprehensively consider the uncertainty and make the results more accurate. The meaning of the triangular fuzzy number is presented in Table 3. The triangular fuzzy judgment matrix M_n×n is constructed, as shown in Eq. (1)(1) $$M_{n\times n}=\left[\begin{array}{cccccc}(1,1,1)& \left(l_{12},m_{12},{\mu }_{12}\right)& \cdots & \left(l_{1i},m_{1i},{\mu }_{1i}\right)& \cdots & \left(l_{1n},m_{1n},{\mu }_{1n}\right)\\ \left(\frac{1}{{\mu }_{12}},\frac{1}{m_{12}},\frac{1}{l_{12}}\right)& (1,1,1)& \cdots & \left(l_{2i},m_{2i},{\mu }_{2i}\right)& \cdots & \left(l_{2n},m_{2n},{\mu }_{2n}\right)\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \left(\frac{1}{{\mu }_{1i}},\frac{1}{m_{1i}},\frac{1}{l_{1i}}\right)& \left(\frac{1}{{\mu }_{2i}},\frac{1}{m_{2i}},\frac{1}{l_{2i}}\right)& \cdots & (1,1,1)& \cdots & \left(l_{in},m_{in},{\mu }_{in}\right)\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \left(\frac{1}{{\mu }_{1n}},\frac{1}{m_{1n}},\frac{1}{l_{1n}}\right)& \left(\frac{1}{{\mu }_{2n}},\frac{1}{m_{2n}},\frac{1}{l_{2n}}\right)& \cdots & \left(\frac{1}{{\mu }_{in}},\frac{1}{m_{in}},\frac{1}{l_{in}}\right)& \cdots & (1,1,1)\end{array}\right]$$(1) : (1) $$M_{n\times n}=\left[\begin{array}{cccccc}(1,1,1)& \left(l_{12},m_{12},{\mu }_{12}\right)& \cdots & \left(l_{1i},m_{1i},{\mu }_{1i}\right)& \cdots & \left(l_{1n},m_{1n},{\mu }_{1n}\right)\\ \left(\frac{1}{{\mu }_{12}},\frac{1}{m_{12}},\frac{1}{l_{12}}\right)& (1,1,1)& \cdots & \left(l_{2i},m_{2i},{\mu }_{2i}\right)& \cdots & \left(l_{2n},m_{2n},{\mu }_{2n}\right)\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \left(\frac{1}{{\mu }_{1i}},\frac{1}{m_{1i}},\frac{1}{l_{1i}}\right)& \left(\frac{1}{{\mu }_{2i}},\frac{1}{m_{2i}},\frac{1}{l_{2i}}\right)& \cdots & (1,1,1)& \cdots & \left(l_{in},m_{in},{\mu }_{in}\right)\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \left(\frac{1}{{\mu }_{1n}},\frac{1}{m_{1n}},\frac{1}{l_{1n}}\right)& \left(\frac{1}{{\mu }_{2n}},\frac{1}{m_{2n}},\frac{1}{l_{2n}}\right)& \cdots & \left(\frac{1}{{\mu }_{in}},\frac{1}{m_{in}},\frac{1}{l_{in}}\right)& \cdots & (1,1,1)\end{array}\right]$$(1) where l is the minimum probability of risk occurrence, m is the median probability of risk occurrence, and μ is the maximum probability of risk occurrence.

Table 3. Reciprocal of triangular fuzzy numbers and their meanings (Adapted from Lyu et al. 2019).

Degree of importance	RFN	TFN	RTFN
Equally important	1	(1,1,1)	(1,1,1)
Almost equally important	1′	(1,1,3)	(1/3,1,1)
In between	2′	(1,2,4)	(1/4,1/2,1)
Slightly important	3′	(1,3,5)	(1/5,1/3,1)
In between	4′	(2,4,6)	(1/6,1/4,1/2)
important	5′	(3,5,7)	(1/7,1/5,1/3)
In between	6′	(4,6,8)	(1/8,1/6,1/4)
Obviously important	7′	(5,7,9)	(1/9,1/7,1/5)
In between	8′	(6,8,10)	(1/10,1/8,1/6)
Extremely important	9′	(7,9,11)	(1/11,1/9,1/7)

2.2.2. Calculation of factor weights

With the establishment of the triangular fuzzy number judgment matrix, the fuzzy synthesis degree F_i of the expert scores and the sum of the triangular fuzzy numbers S_i can be calculated using Eqs. (2)–(4) (Lyu et al. 2019). (2) $$F_i=S_i\times {\left[\sum _{i=1}^n\sum _{j=1}^n{F}_{mi}^j\right]}^{-1}$$(2) (3) $$S_i=\sum _{j=1}^n{F}_{m1}^j=\left(\sum _{j=1}^n{l}_j,\sum _{j=1}^n{m}_j,\sum _{j=1}^n{\mu }_j\right)$$(3) (4) $${\left[\sum _{i=1}^n\sum _{j=1}^n{F}_{mi}^j\right]}^{-1}=\left(\frac{1}{\sum _{i=1}^n\sum _{j=1}^n{\mu }_i^j},\frac{1}{\sum _{i=1}^n\sum _{j=1}^n{m}_i^j},\frac{1}{\sum _{i=1}^n\sum _{j=1}^n{l}_i^j}\right)$$(4)

Assuming that the obtained fuzzy synthesis degrees are F₁ and F₂, when F₁ > F₂, the intersection diagram of the triangular fuzzy function is as shown in Figure 3. Point C, which intersects the two triangular fuzzy numbers in Figure 3, is called the confidence of the fuzzy judgment and is represented by d_i. The value of d_i can be expressed using a piecewise function μ(d), and the confidence that the ith triangular fuzzy number F_i is greater than the k-th triangular fuzzy number F_k can be calculated using Eqs. (5)(5) $$\mu (d)=\{\begin{array}{cc}1\hfill & \left(m_1\ge m_2\right)\hfill \\ 0\hfill & \left(l_2\ge {\mu }_1\right)\hfill \\ \frac{\left(l_2-{\mu }_1\right)}{\left(m_1-{\mu }_1\right)-\left(m_2-l_2\right)}\hfill & (\text{other})\hfill \end{array}$$(5) and (6)(6) $$\mu \left(F_i\ge F_1,F_2,\dots \dots ,F_k\right)=\min \left[\mu \left(F_i\ge F_1\right),\mu \left(F_i\ge F_2\right),\dots \dots ,\mu \left(F_i\ge F_k\right)\right]$$(6) (Lyu et al. 2019). (5) $$\mu (d)=\{\begin{array}{cc}1\hfill & \left(m_1\ge m_2\right)\hfill \\ 0\hfill & \left(l_2\ge {\mu }_1\right)\hfill \\ \frac{\left(l_2-{\mu }_1\right)}{\left(m_1-{\mu }_1\right)-\left(m_2-l_2\right)}\hfill & (\text{other})\hfill \end{array}$$(5) (6) $$\mu \left(F_i\ge F_1,F_2,\dots \dots ,F_k\right)=\min \left[\mu \left(F_i\ge F_1\right),\mu \left(F_i\ge F_2\right),\dots \dots ,\mu \left(F_i\ge F_k\right)\right]$$(6)

Figure 3. Triangular membership function (F₁ > F₂). (Adapted from Lyu et al. 2019).

When μ(d_i) = min[μ(F_i ≥ F_k)](k = 1,2,3,…n, k ≠ i), for the same standard layer, the weights of each risk factor can be calculated using Eqs. (7)(7) $$w_0={\left(\mu {\left(d_1\right)}^{\prime },\mu {\left(d_2\right)}^{\prime },\dots \dots \mu {\left(d_n\right)}^{\prime }\right)}^T$$(7) and (8)(8) $$\mu {\left(d_i\right)}^{\prime }=\frac{\mu \left(d_i\right)}{\sum _{i=1}^n\mu \left(d_i\right)}$$(8) (Lyu et al. 2019). (7) $$w_0={\left(\mu {\left(d_1\right)}^{\prime },\mu {\left(d_2\right)}^{\prime },\dots \dots \mu {\left(d_n\right)}^{\prime }\right)}^T$$(7) (8) $$\mu {\left(d_i\right)}^{\prime }=\frac{\mu \left(d_i\right)}{\sum _{i=1}^n\mu \left(d_i\right)}$$(8)

2.2.3. Consistency

A consistency check was performed to assess the coherence among important risk factors expressed through the consistency ratio (CR). The CR value was calculated using Eq. (9)(9) $$CR=\frac{CI}{RI}$$(9) , and if CR ≤ 0.1, it indicates consistency. The value of CR is calculated as follows: (9) $$CR=\frac{CI}{RI}$$(9) where CI = (λ_max−n)/(n−1), n is the order of the matrix, and λ_max is the maximum eigenvalue of the matrix calculated using Eq. (10)(10) $${\lambda }_{\max }=\frac{1}{n}\sum _{i=1}^n\frac{\sum _{j=1}^n{m}_{ij}{w}_i}{w_i}$$(10) . When n = 1 or 2, no consistency checks are required. The values of the average random consistency index RI are listed in Table 4. (10) $${\lambda }_{\max }=\frac{1}{n}\sum _{i=1}^n\frac{\sum _{j=1}^n{m}_{ij}{w}_i}{w_i}$$(10) where w_i is the weight of the risk factor.

Table 4. The values of RI for judgment matrices of order 1 to 9.

n	1	2	3	4	5	6	7	8	9
RI	0	0	0.52	0.89	1.12	1.26	1.36	1.41	1.46

2.3. Risk grading via VIKOR

2.3.1. Decision index standardization

Different risk factors have different indicators. Therefore, there are dimensional and unit differences between decision indicators, and it is necessary to carry out dimensional normalisation processing in the calculation of the risk level. Then, a standardisation calculation of the factors is performed using Eqs. (11)(11) $$r_{ij}=\left(x_{ij}-x_{ij}^{-}\right)/\left(x_{ij}^{+}-x_{ij}^{-}\right)$$(11) and (12)(12) $$r_{ij}=\left(x_{ij}^{+}-x_{ij}\right)/\left(x_{ij}^{+}-x_{ij}^{-}\right)$$(12) (Atangana Njock et al. 2022):

If x_ij is a positive indicator, it is normalised according to Eq. (11)(11) $$r_{ij}=\left(x_{ij}-x_{ij}^{-}\right)/\left(x_{ij}^{+}-x_{ij}^{-}\right)$$(11) (11) $$r_{ij}=\left(x_{ij}-x_{ij}^{-}\right)/\left(x_{ij}^{+}-x_{ij}^{-}\right)$$(11)

If x_ij is a negative indicator, it is normalised according to Eq. (12)(12) $$r_{ij}=\left(x_{ij}^{+}-x_{ij}\right)/\left(x_{ij}^{+}-x_{ij}^{-}\right)$$(12) (12) $$r_{ij}=\left(x_{ij}^{+}-x_{ij}\right)/\left(x_{ij}^{+}-x_{ij}^{-}\right)$$(12) where x_ij is the decision indicator, r_ij is the standardised result value, x_ij⁺=max(x_ij), x_ij^-=min(x_ij).

2.3.2. Positive and negative ideal solutions

Equation (13)(13) $$\{\begin{array}{c}{r}^{+}=\left\{\max r_{i1},\max r_{i2}\dots \max r_{in}\right\}\\ r^{-}=\left\{\min r_{i1},\min r_{i2}\dots \min r_{in}\right\}\end{array}$$(13) (Atangana Njock et al. 2022) is used to calculate the positive and negative ideal solutions for each decision index. (13) $$\{\begin{array}{c}{r}^{+}=\left\{\max r_{i1},\max r_{i2}\dots \max r_{in}\right\}\\ r^{-}=\left\{\min r_{i1},\min r_{i2}\dots \min r_{in}\right\}\end{array}$$(13) where r⁺ is a positive ideal solution, and r^- is a negative ideal solution.

2.3.3. Group benefit value S_i and individual regret value R_i

Equations (14)(14) $$S_i=\sum _{j=1}^n{w}_j\left(\frac{r^{+}-r_{ij}}{r^{+}-r^{-}}\right)$$(14) and (15)(15) $$R_i=\max \left\{w_j\left(\frac{r^{+}-r_{ij}}{r^{+}-r^{-}}\right)\right\}$$(15) (Atangana Njock et al. 2022) are used to calculate the group benefit value S_i and individual regret value R_i. (14) $$S_i=\sum _{j=1}^n{w}_j\left(\frac{r^{+}-r_{ij}}{r^{+}-r^{-}}\right)$$(14) (15) $$R_i=\max \left\{w_j\left(\frac{r^{+}-r_{ij}}{r^{+}-r^{-}}\right)\right\}$$(15) where w_j is the weight of the decision value x_ij.

2.3.4. Compromise decision index value Q_i

Equation (16)(16) $$Q_i=\mathit{lambda}\frac{S_i-S^{-}}{S^{+}-S^{-}}+(1-\mathit{lambda})\frac{R_i-R^{-}}{R^{+}-R^{-}}$$(16) (Atangana Njock et al. 2022) is used to calculate the compromise decision index value Q_i. (16) $$Q_i=\mathit{lambda}\frac{S_i-S^{-}}{S^{+}-S^{-}}+(1-\mathit{lambda})\frac{R_i-R^{-}}{R^{+}-R^{-}}$$(16) where S⁺=max(S_i), S⁻=min(S_i), R⁺=max(R_i), R⁻=min(R_i). lambda is the decision mechanism coefficient, which represents the risk appetite. The default value is 0.5 (Atangana Njock et al. 2022). If lambda > 0.5, a selection evaluation is performed according to the maximisation of the group utility value. If lambda < 0.5, then the selection evaluation is performed according to the minimisation of the individual regret value. The Q values are sorted to select the best solution.

3. Case study

3.1. Project overview

In this study, the excavation of the Guimintou Headquarters Base in Nanning, Guangxi, China was employed as an engineering case. The Guimintou Excavation suffered a slope collapse accident on 21 May 2022. As shown in Figure 4, the excavation is situated in Yongning District, which lies southeast of Nanning City and is characterised by a basin landform (see Figure 4). Figure 5a illustrates the layout of the excavation, which is located in the central area of the city and surrounded by a dense network of buildings and roads. Notably, the building closest to the excavation is located directly south of it, with the parking shed of the Datang family community situated above the slope where the accident occurred. The tallest nearby building is approximately 80 m high. Figure 5b shows the detailed layout of the pit and accident site. The planned buildings are expected to exceed 200 m in height, resulting in a excavation measuring approximately 300 m in length, 200 m in width, and 15 m in depth. According to the standard (Decree of the Ministry of Housing and Urban Rural Development of the People’s Republic of China (DMHURD-PRC), 2018), the pit qualifies as deep. The accident occurred in the southern part of the pit and the middle of the slope, and the specific site of collapse is marked with a yellow circle (Figure 5b). Specifically, Site A denotes the actual location of the slope collapse, whereas Site B represents the location of the building floor.

Figure 4. Geographical location of the foundation pit.

Figure 5. Accident location: (a) foundation pit plan; (b) foundation pit details (adapted from Baidu map).

Figure 6 shows on-site photographs of the accident at sites A and B. As shown in Figure 6a, the excavation pit suffered a V-shaped collapse, characterised by an upper opening length of approximately 50 m, a lower opening length of approximately 30 m, and a depth of approximately 15 m. As depicted in Figure 6b, an electric bicycle shed is situated above the slope of the foundation pit, serving as a long-term stacking load. The collapse led to the burying of the electric bicycle shed, along with numerous electric bicycles from the second district of Shijia, Datang, resulting in serious economic losses. Fortunately, no one was injured during the incident. In addition, according to the local property management (Chutian City Daily (CCD), 2022), ground subsidence on the parking lot floor was detected in April 2021, but it had not been repaired on the day of the accident.

Figure 6. Collapse accident in the Guimintou foundation pit: (a) retaining structure failure; (b) parking shed on the slope (Chutian City Daily (CCD), 2022).

3.2. Data source

The information utilised in this study, including that on the design, construction situation, engineering management, and surrounding environment of the excavation, was collected from various sources. Determine and quantify the risk level criteria for ten risk factors, as presented in Table 5. These factors included the groundwater level (X₁₁) and soil composition (X₁₃), which were derived from the geological information provided in the construction plan for a project located less than 200 m west of the accident site for the Yongning District Second Middle School in Nanning City (Guangxi Dida Construction Engineering Co., Ltd (GDCECL) 2011). This information indicated that the local soil layers from top to bottom consist of mixed fill (0.2–2.3 m thick), red clay (0.6–5.6 m thick), highly weathered silty sandstone (1.2–3 m thick), and old soil (5.51 m thick), with a groundwater depth below 8 m. Additionally, as shown in Figure 7, the risk factor of 24-h precipitation (X₁₂) were identified from the precipitation data of Nanning City in May from the meteorological network and Nanning meteorological Station. Considering the occurrence of surface settlement in the excavation project in 2022 and its proximity to surrounding buildings, the risk factors for surface settlement (X₂₁) and the distance from surrounding buildings (X₂₂) can be determined. Furthermore, unsuitable deep excavation construction techniques such as non-standard excavation design, improper supporting structure, and illegal construction, combined with a relaxed attitude of the management department, can lead to the identification of two additional risk factors: construction technique (X₃₁) and management quality (X₃₂). Finally, the excavation was located in the city centre with high traffic flow, and there was a stacking load on the slope owing to infrastructure of car sheds, which are key considerations for identifying the risk factors: depth of excavation (X₄₁), stacking load (X₄₂), and dynamic load (X₄₃). The dimensions and shapes of the excavation were carefully combined in this assessment.

Figure 7. Meteorological data of Nanning in May (Tian Qi Website (TQW) 2022).

Table 5. Interval division of influential factors.

Factor	LV1	LV2	LV3	LV4	LV5
Groundwater level (X11)	[20,16]	[16,12]	[12,8]	[8,4]	[4,0]
24-hour precipitation (X12)	[0,10]	[[10,25]	[25,50]	[50,100]	[100,250]
Soil composition (X13)	[20,25]	[15,20]	[10,15]	[5,10]	[0,5]
Surface settlement (X21)	[0,2.5]	[2.5,5]	[5,7.5]	[[7.5,10]	[10,12.5]
Distance from surrounding buildings (X22)	[40,50]	[30,40]	[20,30]	[10,20]	[0,10]
Construction technique (X31)	[80,100]	[60,80]	[40,60]	[20,40]	[0,20]
Management quality (X32)	[80,100]	[60,80]	[40,60]	[20,40]	[0,20]
Depth of excavation (X41)	[0,10]	[10,20]	[20,30]	[30,40]	[40,50]
Stacking load (X42)	[0,20]	[20,40]	[40,60]	[60,80]	[80,100]
Dynamic load (X43)	[0,20]	[20,40]	[40,60]	[60,80]	[80,100]

Referring to previous case studies (Lin et al. 2021, 2023c), the standard specifications for excavations, and the actual situation of the Guimintou excavation project, the identified impact factors were divided into five levels, as listed in Table 5. Among the ten risk factors, X₃₁, X₃₂, X₄₂ and X₄₃ are described by fuzzy qualitative language, which were assigned values ranging from 0 to 100 by expert evaluation (see Table 5), whereas the other six factors were all measurable variables. Specifically, X₁₁ can be classified based on the local groundwater depth; X₁₂ is categorised according to the standards available on the National Meteorological Network (Tian Qi Website (TQW) 2022); the evaluation criteria for X₁₃, X₂₁, and X₂₂ can be obtained from the study of Lin et al. (2021, 2023c); and X₄₁ is divided in accordance with the national excavation standards and specifications.

3.3. Weight of risk factors

In this study, the FAHP was used to calculate the weights of the risk factors. First, a hierarchical framework was established, as shown in Figure 8. Secondly, online questionnaires (https://www.wjx.cn/vm/eieVA0X.aspx#) were utilized to collect opinions from professionals in excavation, tunnel, and geotechnical engineering. Through the questionnaire, participants rated the importance of various risk factors on a scale of 1–9, facilitating a quantitative evaluation. Subsequently, the comparison results of the two factors in the FAHP were replaced with the triangular fuzzy numbers from Table 3, resulting in the judgment matrix presented in Table 6. The weight of each risk factor was calculated using Eqs. (2)(2) $$F_i=S_i\times {\left[\sum _{i=1}^n\sum _{j=1}^n{F}_{mi}^j\right]}^{-1}$$(2) and (8)(8) $$\mu {\left(d_i\right)}^{\prime }=\frac{\mu \left(d_i\right)}{\sum _{i=1}^n\mu \left(d_i\right)}$$(8) , respectively. Figure 9a shows the weight ratio of the excavation index layer, with the highest value assigned to the engineering management index (32.4%), followed by the surrounding environment index (30.2%), construction monitoring indicators (21.1%), and hydrogeological indicators (16.3%). A combined weight distribution of the risk factor layers is shown in Figure 9b, revealing that the risk factor with the greatest weighting is X₃₂ (management quality) at 21.6%, followed by X₂₁ (surface settlement) and X₄₂ (stacking load) with weight shares of 14.1 and 13.7%, respectively. Notably, X₃₂ (management quality) was classified as a high risk factor owing to its high weight. In this case study, there were significant deficiencies in engineering management, as it failed to respond promptly to the slope-cracking phenomenon and exhibited major flaws in project management. This aligns with the results obtained from the framework identification. The results of the consistency test based on the weights of the factors using Eqs. (9)(9) $$CR=\frac{CI}{RI}$$(9) and (10)(10) $${\lambda }_{\max }=\frac{1}{n}\sum _{i=1}^n\frac{\sum _{j=1}^n{m}_{ij}{w}_i}{w_i}$$(10) are listed in Table 6, which indicate that all the results satisfy the consistency requirements.

Figure 8. Hierarchy chart of the potential safety risks in the Guimintou foundation pit.

Figure 9. Weight chart of evaluation index and risk factors: (a) weight of evaluation index. (b) Weight of risk factors.

Table 6. Triangular fuzzy matrix.

Index layer	N1	N2	N3	N4	λmax	CR
N1	[1.00, 1.00, 1.00]	[0.33, 1.00, 1.00]	[0.20, 0.33, 1.00]	[0.25, 0.50 ,1.00]	4.106	0.040
N2	[1.00, 1.00, 3.00]	[1.00, 1.00, 1.00]	[0.25, 0.50, 1.00]	[0.25, 0.50, 1.00]
N3	[1.00, 3.00, 5.00]	[1.00, 2.00, 4.00]	[1.00, 1.00, 1.00]	[1.00, 1.00, 3.00]
N4	[1.00, 2.00, 4.00]	[1.00, 2.00, 4.00]	[0.33, 1.00, 1.00]	[1.00, 1.00, 1.00]
Factor layer	X11	X12	X13		3.065	0.062
X11	[1.00, 1.00, 1.00]	[0.25, 0.50 ,1.00]	[0.33, 1.00, 1.00]
X12	[1.00, 2.00, 4.00]	[1.00, 1.00, 1.00]	[1.00, 2.00, 4.00]
X13	[1.00, 1.00, 3.00]	[0.25, 0.50 ,1.00]	[1.00, 1.00, 1.00]
Factor layer	X21	X22			No consistency check
X21	[1.00, 1.00, 1.00]	[1.00, 2.00, 4.00]
X22	[0.25, 0.50 ,1.00]	[1.00, 1.00, 1.00]
Factor layer	X31	X32			No consistency check
X31	[1.00, 1.00, 1.00]	[0.25, 0.50 ,1.00]
X32	[1.00, 2.00, 4.00]	[1.00, 1.00, 1.00]
Factor layer	X41	X42	X43		3.093	0.089
X41	[1.00, 1.00, 1.00]	[0.25, 0.50 ,1.00]	[1.00, 2.00, 4.00]
X42	[1.00, 2.00, 4.00]	[1.00, 1.00, 1.00]	[1.00, 3.00, 5.00]
X43	[0.25, 0.50 ,1.00]	[0.20, 0.33, 1.00]	[1.00, 1.00, 1.00]

3.4. Risk grading results

After obtaining the weights of each factor, decision makers need to evaluate the risk level of excavation. Referring to previous cases and combining the evaluation of various factors by experts in the field, this study scored the corresponding ten factors, and collected and sorted out the evaluation results, as listed in Table 7. The data were normalised using Eqs. (11)(11) $$r_{ij}=\left(x_{ij}-x_{ij}^{-}\right)/\left(x_{ij}^{+}-x_{ij}^{-}\right)$$(11) and (12)(12) $$r_{ij}=\left(x_{ij}^{+}-x_{ij}\right)/\left(x_{ij}^{+}-x_{ij}^{-}\right)$$(12) to produce the normalisation matrices presented in Table 8. The boundary criteria for the levels of the risk factors were calculated using Eqs. (13)–(16), as listed in Table 9, and the risk levels are shown in Figure 10. Specifically, when the compromise decision value Q falls within the range of [0, 0.194], the risk level is classified as the first level (very low risk); within the range of (0.194, 0.389], it is in the second level (low risk); (0.389, 0.585] corresponds to the third level (median risk); (0.585, 0.785] is the fourth level (high risk); and (0.785, 1] indicates the fifth level (very high risk). A higher risk level implies a higher accident probability. In this case study, by incorporating the parameters from Table 7 into the structural framework, the compromise decision index value of the pit was calculated as 0.646. According to the rating criteria shown in Figure 10, the Guimintou Pit was at a high risk stage, necessitating the implementation of appropriate treatment measures and adjustments to the construction plan.

Figure 10. Risk level chart.

Table 7. Scoring table for risk factor of the excavation.

Risk factor	X11	X12	X13	X21	X22	X31	X32	X41	X42	X43
rate	8	25	20	12.5	0	40	40	15	100	40

Table 8. Square normalization matrix.

Factor	X11	X12	X13	X21	X22	X31	X32	X41	X42	X43	S	R	Q
LV1	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
LV2	0.008	0.003	0.010	0.028	0.014	0.022	0.043	0.021	0.027	0.012	0.188	0.043	0.194
LV3	0.015	0.007	0.020	0.056	0.028	0.043	0.086	0.042	0.055	0.024	0.378	0.086	0.389
LV4	0.023	0.015	0.031	0.085	0.042	0.065	0.130	0.063	0.082	0.036	0.570	0.130	0.585
LV5	0.030	0.030	0.041	0.113	0.056	0.086	0.173	0.084	0.110	0.048	0.770	0.173	0.785
LV6	0.038	0.074	0.051	0.141	0.070	0.108	0.216	0.105	0.137	0.060	1.000	0.216	1.000

Table 9. Boundary standards of risk factor grade.

	LV1		LV2		LV3		LV4		LV5
Standard value	L	R	L	R	L	R	L	R	L	R
	0.00	0.194	0.194	0.389	0.389	0.585	0.585	0.785	0.785	1.00

4. Discussion

4.1. Case study analysis

The results of the case study indicated that there are significant risks associated with Guimintou excavation project. Notably, three pivotal risk factors are identified: surface settlement (X₂₁, 14.1%), management quality (X₃₂, 21.6%), and stacking load (X₄₂, 13.7%), among which X₃₂ emerging as the most critical risk factor. As excavation progressed, continuous construction and soil compression resulted in notable soil volume changes and subsequent settlement. The surface of the collapse point had already shown minor cracks one year before the accident occurred. In addition, the cumulative load’s effect on the slope became increasingly evident, highlighting the urgent necessity for timely clearance of accumulated loads from the slope. In this instance, the surrounding vehicles imposed considerable dynamic loads, increasing the potential for accidents. Moreover, the significance of management quality resonated throughout the project. In this case, the construction of a parking shed on top of the excavation slope and the occurrence of cracks on the shed surface indicated significant vulnerabilities, which were coupled with poor management quality and insufficient attention to these issues. As a result, consistent with the risk assessment results, the collapse accident occurred. The sorting results of VIKOR indicated that the excavation was at high risk (the compromise decision index value was 0.646). This underscores the need for timely monitoring, prompt remedial measures, and adjustments to the construction schedules. Such proactive measures could have prevented this collapse.

To validate the enhancements of the proposed method, a comparative analysis between FAHP, traditional AHP, and traditional Precedence Chart (PC) is conducted, with all methods showcasing similar weight trends, as illustrated in Figure 11. All three methods consistently identified X₃₂ as the primary high risk factor. However, FAHP assigned a higher weight of X₃₂ than the traditional methods, enhancing the recognition of high risk factors. Notably, experts attributed similar scores for factors X₁₁ and X₁₃, and FAHP offers a more refined approach. FAHP can comprehensively consider the uncertainty and inconsistency of expert opinions, resulting in a more precise differentiation between these two risk factors, whereas AHP and PC yielded identical weights. Additionally, Figure 12 presents the comparison between the computational results of FAHP-VIKOR and the traditional FAHP-TOPSIS method, emphasizing the compromise decision index value Q as determined by Eq. (16)(16) $$Q_i=\mathit{lambda}\frac{S_i-S^{-}}{S^{+}-S^{-}}+(1-\mathit{lambda})\frac{R_i-R^{-}}{R^{+}-R^{-}}$$(16) in Section 2.3.4. Significantly, the FAHP-VIKOR method assesses the risk level as the fourth level, in contrast to the third level identified by the FAHP-TOPSIS method (see Figure 12). According to the practical case, the assessment result of FAHP-VIKOR method prove to be more accurate, effectively reflecting the heightened risk of the collapse accident in urban excavation. As shown in Figure 10, the FAHP-VIKOR method offers a comprehensive risk level of the whole project combined with all risk factors, providing a clearer assessment of the project’s overall risk.

Figure 11. Comparison of FAHP, AHP, and PC weight results.

Figure 12. Comparison of calculation results between FAHP-VIKOR and FAHP-TOPSIS.

4.2. Perspective management

Risk assessment plays a pivotal role in pre-emptively ensuring project safety and preventing potential hazards. This process serves as a means of gauging the magnitude of inherent risk in a project. It comprises three crucial phases: risk identification, risk analysis, and risk evaluation. The initial phase involves identifying the various risk factors that may culminate in disasters. Subsequently, these risk factors are comprehensively evaluated using methods such as the AHP and fuzzy comprehensive evaluation. Ultimately, the analysis results are subjected to evaluation, thereby forming the foundation for decision-making. Risk assessment can effectively predict and warn of disasters and accidents, and reduce economic losses and casualties. Furthermore, the field of risk assessment is rapidly developing and is bolstered by the integration of cutting-edge methodologies and techniques. This dynamism underscores the critical role of risk assessment in shaping a proactive safety culture in project management. According to the risk assessment results, high risk factors can be accurately identified to implement remedial measures promptly and prevent accidents. According to the case results of this study, specific measures can be quickly proposed: improve the management quality, reinforce the slope cracks in time, and prevent the cracks from evolving into ground settlement. Moreover, the accumulated load on the slope should be cleaned up in time to relieve the pressure on the slope and prevent accidents.

The role of government management in ensuring project safety should be emphasized. Construction management should also be strengthened to prevent similar accidents, such as the collapse of Guimintou excavation. Government departments should enhance the safety awareness of residents through effective and comprehensive public efforts. Cracks occurred in the excavation prior to the collapse; however, the relevant departments did not pay attention to them. With the exacerbation of risks, such as increased rainfall, the potential for slope instability increases, eventually leading to collapse accidents. This accident should serve as a catalyst to attract the attention of the relevant departments, prompting them to strengthen the quality of project management and excavation construction. Simultaneously, it is essential for government departments to effectively promote the awareness of excavation safety among residents. Efforts to enhance the public understanding and awareness of this matter are crucial. Moreover, construction departments should intensify site safety control measures, such as erecting construction walls and displaying potential construction-related issues on walls. Encouraging citizens to actively participate in supervision is highly encouraged.

4.3. Limitations and future work

The identification of risk factors is critical in this framework. The risk factors within the hierarchy are identified according to the situation of the case, and the application of the framework to other cases needs to be modified according to the actual situation. Currently, the prevailing approach to identify risk factors relies on manual collection and identification. An evident constraint is the selective consideration of high risk factors in a specific excavation project without a comprehensive collection of risk-related data, which poses a substantial limitation. With the development of computer technology, artificial intelligence systems with comprehensive, accurate, and efficient capabilities for identification and processing of data have emerged. The combination of technologies, such as GIS, remote sensing (RS), global positioning system (GPS), and neural networks (Zheng et al. 2021, 2022; Shi and Wang 2022), fosters swifter and more precise identification of risk factors. The integration of artificial intelligence with practical engineering has become a future development trend, and the identification framework proposed in this study has significant potential for advancements in this dynamic landscape.

5. Conclusions

In this study, a novel FAHP-VIKOR framework was developed for assessment and management of risks in urban excavation projects. It provides a new approach for risk management of excavation during construction. An excavation project was selected to demonstrate the potential and applicability of the proposed approach. The major findings of this study are as follows:

1. The proposed FAHP-VIKOR framework was developed by integrating the FAHP and VIKOR methods to identify and manage high risk factors during urban excavation. In this approach, the FAHP is applied to calculate the risk factor weights, whereas VIKOR is utilised to assess the risk level. Ultimately, the framework identifies high risk factors and risk levels for urban excavation projects, which facilitates the implementation of targeted measures and informed decisions, thereby ensuring efficient and safe construction.

2. A synthesis of data-driven quantitative analysis and qualitative methodologies is introduced to enhance the accuracy and authenticity of the assessment results. This involves conducting quantitative analyses using comprehensive data on the hydrogeology, construction monitoring, and environmental factors. Qualitative investigations focus primarily on management considerations. This fusion amplifies the accuracy of the risk assessment findings, strengthens the overall validity, and contributes to a more effective risk management strategy.

3. Using an excavation project in Nanning City, China, as a case study, a total of ten risk factors were identified from four different aspects through comprehensive data collection. The model effectively calculates the risk factor weights, aligning them closely with actual project circumstances. Most notably, a compromise decision index value of 0.646 distinctly positioned the excavation within a high risk stage (level 4). The efficacy of the proposed approach was validated considering the occurrence of a slope-collapse accident within the pit.

4. The proposed approach could emerge as a robust tool for risk assessment in urban excavation engineering. The integration of project-specific risk factors within the framework yields practical assessment results. However, notable limitations arise from the sources of information and dependence on human-involved data collection. Anticipating technological advancements, the integration of automated data collection holds promises for enhancing the framework’s capabilities and opening avenues for future research and development in this field.

Authors’ contribution

Xiang Liu: Writing- Original draft preparation, Investigation, Methodology, Software, Visualization. Xin-Hui Zhou: Conceptualization, Writing - Reviewing and Editing, Data curation. Ya-Jie Wang: Investigation, Writing - Reviewing and Editing.

Disclosure statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

Data will be made available on request.

Additional information

Funding

The corresponding author would like to thank the China Scholarship Council for providing a visiting PhD scholarship [Grant No. 202306230006] in Singapore.