Post-examination interpretation of objective test data: Monitoring and improving the quality of high-stakes examinations: AMEE Guide No. 66

Abstract

The purpose of this Guide is to provide both logical and empirical evidence for medical teachers to improve their objective tests by appropriate interpretation of post-examination analysis. This requires a description and explanation of some basic statistical and psychometric concepts derived from both Classical Test Theory (CTT) and Item Response Theory (IRT) such as: descriptive statistics, explanatory and confirmatory factor analysis, Generalisability Theory and Rasch modelling. CTT is concerned with the overall reliability of a test whereas IRT can be used to identify the behaviour of individual test items and how they interact with individual student abilities. We have provided the reader with practical examples clarifying the use of these frameworks in test development and for research purposes.

Introduction

The output of the examination process is transferred to students either formatively, in the form of feedback, or summatively, as a formal judgement on performance. Clearly, to produce an output which fulfils the needs of students and the public, it is necessary to define, monitor and control the inputs to the process. Classical Test Theory (CTT) assumes that inputs to post-examination analysis contain sources of measurement error that can influence the student's observed scores of knowledge and competencies. Sources of measurement error is derived from test construction, administration, scoring and interpretation of performance. For example; quality variation among knowledge-based questions, differences between raters, differences between candidates and variation between standardised patients (SPs) within an Objective Structured Clinical Examination (OSCE).

To improve the quality of high-stakes examinations, errors should be minimised and, if possible, eliminated. CTT assumes that minimising or eliminating sources of measurement errors will cause the observed score to approach the true score. Reliability is the key estimate showing the amount of measurement error in a test. A simple interpretation is that reliability is the correlation of the test with itself; squaring this correlation, multiplying it by 100 and subtracting from 100 gives the percentage error in the test. For example, if an examination has a reliability of 0.80, there is 36% error variance (random error) in the scores. As the estimate of reliability increases, the fraction of a test score that is attributable to error will decrease. Conversely, if the amount of error increases, reliability estimates will decrease (Nunnally & Bernstein 1994).

Although some medical schools have adopted psychometric methods such as reliability testing and item analysis to monitor and improve OSCE examination (Lawson 2006; Iramaneerat et al. 2008), the use of advanced psychometric methods such as generalisability theory and Rasch modelling has yet to become widespread.

Therefore, the objective of this Guide is to illustrate the use and interpretation of traditional and advanced psychometric methods using several examples. Ultimately, readers are encouraged to consider using these methods with their own exam data. We have explained how to generate post-examination data from objective tests using SPSS elsewhere (Tavakol & Dennick 2011b), and therefore we will not discuss these methods in this article. We shall begin with the traditional interpretation of post-exam data from objective tests and OSCEs and then look at the application of modern psychometric methods. We will use simulated data to exemplify methods for improving subsequent examinations.

Table

Practice points

Health profession educators need to interpret test data using psychometric methods. EFA describes how and to what extent a group of items in a test are related to a set of latent constructs or factors. CFA confirms the modelled relationship between the assessed factors. Generalisability theory extends CTT allowing assessors to isolate and estimate multiple errors that are influencing the results of a test. IRT, including Rasch modelling, produces a variety of data displays, encapsulating both student and item properties that enable test developers to monitor and improve the quality of test questions.

Interpretation of basic post-examination results

Individual questions

A descriptive analysis is the first step in summarising and presenting the raw data of an examination. A distribution frequency for each question immediately shows up the number of missing questions and the patterns of guessing behaviour. For example, if there were no missing question responses identified, this would suggest that students either had good knowledge or were guessing for some questions. Conversely, if there were missing question responses, this might be either an indication of an inadequate time for completing the examination, a particularly hard exam or negative marking is being used (Stone & Yeh 2006; Reeve et al. 2007).

The means and variances of test questions can provide us with important information about each question. The mean of a dichotomous question, scored either 0 or 1, is equal to the proportion of students who answer correctly, denoted by p. The variance of a dichotomous question is calculated from the proportion of students who answer a question correctly (p) multiplied by those who answer the question incorrectly (q). To obtain the standard deviation (SD), we merely take the square root of p × q. For example, if in an objective test, 300 students answered Question 1 correctly and 100 students answered it incorrectly, the p value for Question 1 will be equal to 0.75 (300/400), and the variance and SD will be 0.18 (0.75 × 0.25) and 0.42 respectively. The SD is useful as a measure of variation or dispersion within a given question. A low SD indicates that the question is either too easy or too hard. For example, in the above example, the SD is low indicating that the item is too easy. Given the item difficulty of Question 1 (0.75) and a low item SD, one can conclude that responses to item was not dispersed (there is little variability on the question) as most students paid attention to the correct response. If the question had a high variability with a mean at the centre of distribution, the question might be useful.

Total performance

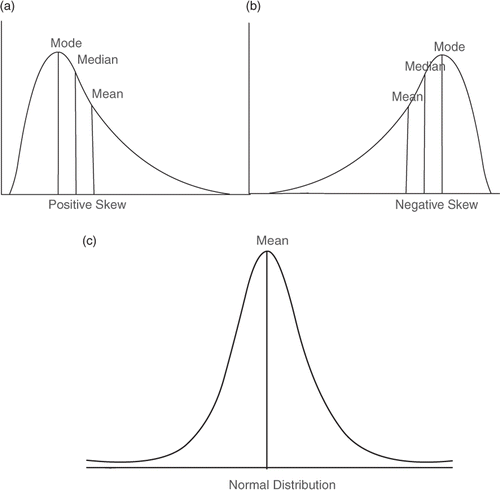
After obtaining the mean and SD for each question, the test can be subjected to conventional performance analysis where the sum of correct responses of each student for each item is obtained and then the mean and SD of the total performance are calculated. Creating a histogram using SPSS allows us to understand the distribution of marks on a given test. Students’ marks can take either a normal distribution or may be skewed to the left or right or distributed in a rectangular shape. Figure 1(a) illustrates a positively skewed distribution. This simply shows that most students have a low-to-moderate mark and a few students received a relatively high mark in the tail. In a positively skewed distribution, the mode and the median are greater than the mean indicating that the questions were hard for most students. Figure 1(b) shows a negatively skewed distribution of students’ marks. This shows that most students have a moderate-to-high mark and a few students received relatively a low mark in the tail. In a negatively skewed distribution, the mode and the median are less than the mean indicating that the questions were easy for most students.

Figure 1. Some shapes of distributions.

Figure 1(c) shows most marks distributed in the centre of a symmetrical distribution curve. This means that half the students scored greater than the mean and half less than mean. The mean, mode and median are identical in this situation. Based on this information, it is hard to judge whether the exam is hard or easy unless we obtain differences between the mode, median or mean plus an estimate of the SD. We have explained how to compute these statistics using SPSS elsewhere (Tavakol & Dennick 2011b; Tavakol & Dennick 2012).

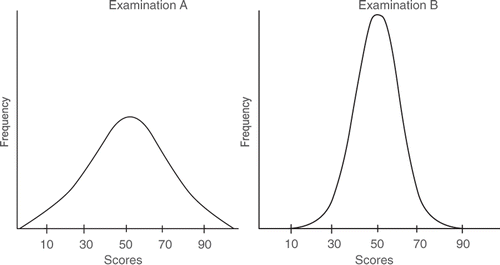
As an example, we would ask you to consider the two distributions in Figure 2, which represent simulated marks of students in two examinations.

Figure 2. Two different distributions from two examinations.

Both the mark distributions have a mean of 50, but show a different pattern. Examination A has a wide range of marks, with some below 20 and some above 90. Examination B, on the other hand, shows few students at either extreme. Using this information, we can say that Examination A is more heterogeneous than Examination B and that Examination B is more homogenous than Examination A.

In order to better interpret the exam data, we need to obtain the SD for each distribution. For example, if the mean marks for the two examinations are 67.0, with different SDs of 6.0 and 3.0, respectively, we can say that the examination with a SD of 3.0 is more homogenous and hence more consistent in measuring performance than the examination with a SD of 6.0. A further interpretation of the value of the SD is how much it shows students’ marks deviating from the mean. This simply indicates the degree of error when we use a mean to explain the total student marks. The SD also can be used for interpreting the relative position of individual students in a normal distribution. We have explained and interpreted it elsewhere (Tavakol & Dennick 2011a).

Interpretation of classical item analysis

In scientific disciplines, it is often possible to measure variables with a great deal of accuracy and objectivity but when measuring student performance on a given test due to a wide variety of confounding factors and errors, this accuracy and objectivity becomes more difficult to obtain. For instance, if a test is administrated to a student, he or she will obtain a variety of scores on different occasions, due to measurement errors affecting his or her score. Under CTT, the student's score on a given test is a function of the student's true score plus random errors (Alagumalai & Curtis 2010), which can fluctuate from time to time. Due to the presence of random errors influencing examinations, we are unable to exactly determine a student's true score unless they take the exam an infinite number of times. Computing the mean score in all exams would eliminate random errors resulting in the student's score eventually equalling the true score. However, it is practically impossible to take a test an infinite number of times. Instead we ask an infinite number of students (in reality a large cohort!) to take the test once allowing us to estimate a generalised standard error of measurement (SME) from all the students’ scores. The SME allows us to estimate the true score of each student which has been discussed elsewhere (Tavakol & Dennick 2011b).

Reliability

It is worth reiterating here that just as the observed score is composed of the sum of the true score and the error score, the variance of the observed score in an examination is made up of the sum of the variances of the true score and the error score, which can be formulated as follows:

Now imagine a test has been administered to the same cohort several times. If there is a discrepancy between the variance of the observed scores for each individual, on each test, the reliability of the test will be low. The test reliability is defined as the ratio of the variance of the true score to the variance of the observed score:

Given this, the greater the ratio of the true score variance to the observed score variance, the more reliable the test. If we substitute variance (true scores) from Equation (1) in Equation (2), the reliability will be as follows:

And then we can rearrange the reliability index as follows:

This equation simply shows the relationship between source of measurement error and reliability. For example, if a test has no random errors, the reliability index is 1, whereas if the amount of error increases, the reliability estimate will decrease.

Increasing the test reliability

The statistical procedures employed for estimating reliability are Cronbach's alpha and the Kuder–Richardson 20 formula (KR-20). If the test reliability was less than 0.70, you may need to consider removing questions with low item-total correlation. For example, we have created a simulated SPSS output for four questions in Tables 1 and 2.

Table 1.  Reliability statistics, simulated output from SPSS

Cronbach's alpha	Cronbach's alpha based on standardised items	Number of items
0.725	0.724	4

Table 2.  Item-total statistics

Question	Scale mean if item deleted	Scale variance if item deleted	Corrected item-total correlation	Cronbach's alpha if item deleted
1	1.700	1.04	0.818	0.475
2	1.800	1.06	0.712	0.536
3	1.700	1.046	0.818	0.475
4	2.00	1.86	−0.051	0.950

Table 1 shows Cronbach's alpha for four questions, 0.72. Table 2 shows item-total correlation statistics with the column headed ‘Cronbach's Alpha if Item deleted’. (Item-total correlation is the correlation between an individual question score and the total score).

The fourth question in the test has a total-item correlation of −0.51 implying that responses to this particular question have a negative correlation with the total score. If we remove this question from the test, the alpha of the three remaining questions increase from 0.725 to 0.950, making the test significantly more reliable.

Tables 3 and 4 show the output SPSS after removing Question 4:

Table 3.  Reliability statistics, simulated output from SPSS (after removing Question 4)

Cronbach's alpha	Number of items
0.950	3

Table 4.  Item-total statistics (after removing Question 4)

Question	Scale mean if item deleted	Scale variance if item deleted	Corrected item-total corrections	Cronbach's alpha if item deleted
1	1.400	0.838	0.945	0.889
2	1.300	0.869	0.802	1.00
3	1.400	0.838	0.946	0.889

Tables 3 and 4 illustrate the impact of removing Question 4 from the test, which significantly increases the value of alpha.

However, if we now remove Question 2, the value of the alpha for the test will be perfect, i.e. 1, which means each question in the test must be measuring exactly the same thing. This is not necessarily a good thing as it suggests that there is redundancy in the test, with multiple questions measuring the same construct. If this is the case, the test length could be shortened without compromising the reliability (Nunnally & Bernstein 1994). This is because the reliability is a function of test length. The more the items, the more the reliability of a test.

Although Cronbach's alpha and KR-20 are useful for estimating the reliability of a test, they conflate all sources of measurement error into one value (Mushquash & O'Connor 2006). Recall that true scores equal observed scores plus errors, which is derived from a variety of sources. The influence of each source of error can be estimated by the coefficient of generalisability, which is similar to a reliability estimate in the true score model (Cohen & Swerdlik 2010). Later we will describe how to identify and reduce sources of measurement errors using generalisability theory or G-theory as it is known. What is more, in our previous Guide (Tavakol & Dennick 2012), we explained and interpreted item difficulty level, item discrimination index and point bi-serial coefficient in terms of CTT. In this Guide, we will explain and interpret these concepts in terms of Item Response Theory (IRT) using item characteristic parameters (item difficulty and item discrimination) and the student ability/performance to all questions using the Rasch model.

Factor analysis

Linear factor analysis is widely used by test developers in order to reduce the number of questions and to ensure that important questions are included in the test. For example, the course convenor of cardiology may ask all medical teachers involved in teaching cardiology to provide 10 questions for the exam. This might generate 100 questions, but all these questions are not testing the same set of concepts. Therefore, identifying the pattern of correlations between the questions allows us to discover related questions that are aimed at the underlying factors of the exam. A factor is a construct which represents the relationship between a set of questions and will be generated if the questions are correlated with the factor. In factor analysis language, this refers to factor ‘loadings’. After factor analysis is carried out, related questions load onto factors which represent specific named constructs. Questions with low loadings can therefore be removed or revised.

If a test measures a single trait, only one factor with high loadings will explain the observed question relationships and hence the test is uni-dimensional. If multiple factors are identified, then the test is considered to be multi-dimensional.

There are two main components to linear factor analysis: exploratory and confirmatory. Exploratory Factor Analysis (EFA) identifies the underlying constructs or factors within a test and hypothesises a model relationship between them. Confirmatory Factor Analysis (CFA) validates whether the model fits the data using a new data set. Below, each method is explained.

Exploratory factor analysis

EFA is widely used to identify the relationships between questions and to discover the main factors in a test as previously described. It can be used either for revising exam questions or choosing questions for a specific knowledge domain. For example, if in the cardiology exam we are interested in testing the clinical manifestations of coronary heart disease, we simply look for the questions which load on to this domain. The following simulated example, using an examination with 10 questions taken by 50 students, demonstrates how to improve the questions in an examination. This allows us to demonstrate how to revise and strengthen exam questions and to calculate the loadings on the domain of interest. As well as identifying the factors EFA also calculates the ‘communality’ for each question. To understand the concept of communality, it is necessary to explain the variance (the variability in scores) within the EFA approach.

We have already learnt from descriptive statistics how to calculate the variance of a variable. In the language of factor analysis, the variance of each question consists of two parts. One part can be shared with the other questions, called ‘common variance’; the rest may not be shared with other questions, called ‘error’ or ‘random variance’. The communality for a question is the value of the variance accounted for by the particular set of factors, ranging from 0 to 1.00. For example, a question that has no random variance would have a communality of 1.00; a question that has not shared its variance with other questions would have a communality of 0.00. The communality shown for Question 9 (Table 5) is 0.85, that is 85% of the variance in Question 9 is explained by factor 1 and factor 2, and 15% of the variance of Question 9 has nothing in common with any other question. To compute the shared variances for each question in SPSS, the following steps are carried out in SPSS (SPSS 2009). From the menus, choose ‘Analyse’, ‘Dimension Reduction’ and ‘Factor’, respectively. Then move all questions on to the ‘Variables’ box. Choose ‘Descriptive’ and then click ‘Initial Solution’ and ‘Coefficients’, respectively. Then click ‘Rotation’. Choose ‘Varimax’ and click on ‘Continue’ and then ‘OK’. In Table 5, we have combined the simulated data of the SPSS output together.

Table 5.  Rotated two factors with communalities (h²)

	Question 5 included			After removing Question 5
Question	Factor 1	Factor 2	h^2	Factor 1	Factor 2	h^2
9	0.92	−0.02	0.85	0.92	0.005	0.85
2	0.92	−0.02	0.85	0.92	0.005	0.85
6	0.81	0.21	0.71	0.80	0.24	0.71
10	0.79	−0.38	0.77	0.80	−0.36	0.77
4	0.79	−0.38	0.77	0.80	−0.36	0.77
1	0.73	0.36	0.69	0.72	0.38	0.68
3	0.69	0.16	0.50	0.69	0.18	0.51
5	−0.28	0.03	0.08
7	0.01	0.96	0.92	−0.0017	0.96	0.92
8	0.01	0.96	0.85	−0.0017	0.96	0.92
Percentage of variance explained by each factor	47.23	23.60	70.83	51.80	26.20	78.00

Table 5 shows that two factors have emerged. Factor 1 demonstrates excellent loading with Questions 9, 2, 6, 10, 4, 1 and 3 and Factor 2 demonstrates excellent loading with Questions 7 and 8, indicating these items have a strong correlation with Factors 1 and 2. It should be noted that loadings with values greater than 0.71 are considered excellent (0.71 × 0.71 = 0.50 × 100; i.e. 50% common variance between the item and the factor, or 50% of the variation in the item can be explained by the variation in the factor, or 50% of the variance is accounted for by the item and the factor), 0.63 (40% common variance) very good, 0.45 (20% common variance) fair. Values less than 0.32 (10% common variance) are considered poor and less contribute to the overall test and they should be investigated (Comrey & Lee 1992; Tabachnick & Fidell 2006). Table 5 also shows communalities for each question in the column labelled h². For example, 92% of the variance in Question 2 is explained by the two factors that have emerged from the EFA approach. The lowest communality is for Question 5, indicting 8% of the variance is explained by this question. Low values of less than 30% indicate that the variance of the question does not relate to other questions loaded on to the identified factors. In Table 5, Question 5 has the lowest communality figure and has not loaded onto Factors 1 or 2, suggesting this question should be revised or discarded.

Table 5 also shows the values of variance explained by the two factors that have been identified from the EFA approach; 0.47 of the variance is accounted for by Factor 1 and 0.23 of the variance is accounted for by Factor 2. Therefore, 0.70 of the variance is accounted for by all of the questions. However, if we delete Question 5, we can increase the total variance accounted for to 0.78. A further interpretation of Table 5 is that the vast majority of questions have been loaded on to Factor 1, providing evidence of convergence and discrimination for the construct validity of the test. We can argue that the test is convergent as there are high loadings on to Factor 1. The test is also discriminant as the questions that have loaded on to Factor 1 have not loaded on to Factor 2. This means that Factor 2 measures another construct/concept which is discriminated from Factor 1. Because two factors have been identified, it would be appropriate to calculate Cronbach's alpha co-efficient for each factor because they are measuring two different constructs. It should be noted that items which load on more than two factors need to be investigated.

Confirmatory factor analysis

The technique of CFA has been widely used to validate psychological tests but has been less used to evaluate and improve the psychometric properties of exam questions. The EFA approach can reveal how exam questions are correlated or connected to an underlying domain of factors. For example, an EFA approach may show that the internal structure of a 100 question test consist of three underlying domains, say physical examination, clinical reasoning and communication skills. The number of factors identified constitutes the components of a hypothesised model, the factor structure model. In the above example, the model would be termed a three-factor model. The CFA approach uses the hypothesised model extracted by EFA to confirm the latent (underlying) factors. However, in order to confirm model fitting, a new data set must be used to avoid a circular argument. For example, the same test could be administered to a different but comparable group of students.

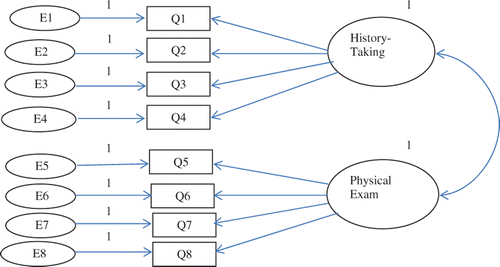
Therefore, educators must first identify a model using EFA and test it using CFA. This approach also allows educators to revise exam questions and the factors underlying their constructs (Floys & Widaman 1995). For example, suppose EFA has revealed a two-factor model from an exam consisting of history-taking and physical examination questions. The researcher wishes to measure the psychometric characteristics of the questions and test the overall fit of the model to improve the validity and reliability of the exam. This can be achieved by the use of structural equation modelling (SEM) which determines the goodness-of-fit of the newly input sample data to the hypothesised model. The model fit is assessed using Chi-square testing and other fit indices. In contrast to other statistical hypothesis testing procedures, if the value of Chi-square is not significant, the new data fit and the model is confirmed. However, as the value of Chi-square is a function of increasing or decreasing sample size, other fit indices should also be investigated (Dimitrov 2010). These indices are the comparative fit index (CFI) and the root mean square error of approximation (RMSEA). A CFI value of greater than 0.90 shows a psychometrically acceptable fit to the exam data. The value of RMSEA needs to be below 0.05 to show a good fit (Tabachnick & Fidell 2006). A RMSEA of zero indicates that the model fit is perfect. It should be noted that CFA can be run by a number of popular statistical software programmes such as SAS, LISREL, AMOS and Mplus. For the purpose of this article, we choose AMOS (Analysis of Moment Structures) for its use of ease. The AMOS software program can easily create models and calculate the value of Chi-square as well as the fit indices. In the above example, a test of 8 questions has two factors, history-taking and physical examination and the variance of these eight exam questions can be explained by these two highly correlated factors. The test developer draws the two-factor model (the path diagram) in AMOS to test the model (Figure 3). Before estimating the parameters of the model, click on the ‘view’ and click on ‘Analysis Properties’ and then click on ‘Minimization history’, Standardised estimates, ‘Squared multiple Correlations’ and ‘Modification indices’. To run the estimation, from the menu at the top, click on ‘Analyze’, then click on ‘Calculate Estimates’.

Figure 3. The two-factor model.

The output is given in Table 6. SEM calculates the slopes and intercepts of calculated correlations between questions and factors. From a CTT, the intercept is analogous to the item difficulty index and the slope (standardised regression weights/coefficients) is analogous to the discrimination index.

Table 6.  Simulated parameters revealed by the two-factor model

Question type	Question number	Intercept	Slope: history-taking	Slope: physical examination
History-taking	1	0.97	0.21	0.50
	2	0.85	0.24	0.32
	3	0.78	0.31	0.02
	4	0.45	−0.03	0.26
Physical examination	1	0.30	0.37	0.19
	2	0.64	0.26	0.27
	3	0.08	0.29	0.22
	4	0.39	0.32	0.16

Table 6 shows that Question 1 in history-taking and Question 3 in physical examination were easy (intercept = 0.97) and hard (0.08), respectively. Table 6 also shows that Question 4 in history-taking is not contributing to overall history-taking score (slope = −0.03). Further analysis was conducted to assess degree of fit model to the exam data. Focusing on Table 7, the absence of significance for the Chi-square value (p = 0.49) implies support for the two- factor model in the new sample. In reviewing values of both CFI and RMSEA in Table 7, it is evident that the two-factor model represents a best fit to the exam data for the new sample.

Table 7.  Goodness-of-fit indices for the two-factor model

Model	χ^2	df	p	CFI	RMSEA
Total sample	33.5	34	0.49	0.97	0.02

Further evidence for the relationship between the history-taking and physical examination components of the test is revealed by the calculation of a 0.70 correlation between the two factors, supporting the hypothesised two-factor model. It should be noted that AMOS will display the correlation between factors/components by clicking the ‘view the output diagram’ button. You can also view correlation estimates from ‘text output’. From the main menu, choose view and then click on ‘text output’.

Generalisability theory analysis

We would ask you to recall that reliability is concerned with the ability of a test to measure students' knowledge and competencies consistently. For example, if students are re-examined with the same items and with the same conditions on different occasions, the results should be more or less the same. In CTT, the items and conditions may be the causes of measurement errors associated with the obtained scores. Reliability estimates, such as KR-20 or Cronbach's alpha, cannot identify the potential sources of measurement error associated with these items and conditions (also known as facets of the test) and cannot discriminate between each one. However, an extension of CTT called Generalisability Theory or G-theory, developed by Lee J. Cronbach and colleagues (Cronbach et al. 1972), attempts to recognise, estimate and isolate these facets allowing test constructors to gain a clearer picture of sources of measurement error for interpreting the true score. One single analysis of, for example, the results of an OSCE examination, using G-theory can estimate all the facets, potentially producing error in the test. Each facet of measurement error has a value associated with it called its variance component, calculated via an analysis of variance (ANOVA) procedure, described below. These variance components are next used to calculate a G-coefficient which is equivalent to the reliability of the test and also enables one to generalise students’ average score over all facets.

For example, imagine an OSCE has used SPs, a range of examiners and various items to assess students' performance on 12 stations. SPs, examiners and items and their interactions (e.g. interaction between SPs and items) are considered as facets of the assessment. The score that the student obtains from the OSCE will be affected by these facets of measurement error and therefore the assessor should estimate the amount of error caused by each facet. Furthermore, we examine students using a test to make a final decision regarding their performance on the test. To make this decision, we need to generalise a test score for each student based on that score. This indicates that assessors should ensure the credibility and trustworthy of the score as means to making a good decision (Raykov & Marcoulides 2011). Therefore, the composition of errors associated with the observed (obtained) scores that gained from a test need to be investigated. G-theory analysis can then provide useful information for test constructors to minimise identified sources of error (Brennan 2001). We will now explain how to calculate the G-coefficient from variance components.

G-coefficient calculation

To calculate the G-coefficient from variance components of facets, test analysers traditionally use the ANOVA procedure. ANOVA is a statistical procedure by which the total variance present in a test is partitioned into two or more components which are sources of measurement error. Using the calculated mean square of each source of variation from the ANOVA output (e.g. SPs, items, assessors, etc.), investigators determine the variance components and then calculate the G-coefficient from these values.

However, SPSS and other statistical packages like the Statistical Analysis System (SAS) now allow us to calculate the variance components directly from the test data. We will now illustrate how to obtain the variance components from SPSS directly for calculating the G-coefficient. The procedure used varies according to the number of facets in the test. There are single facet and multiple facet designs as described below.

Single facet design

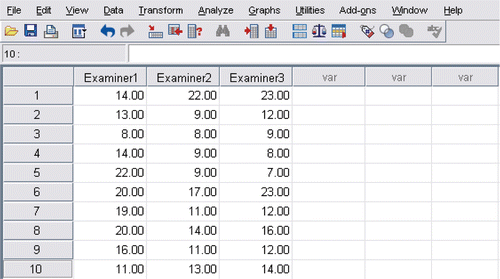
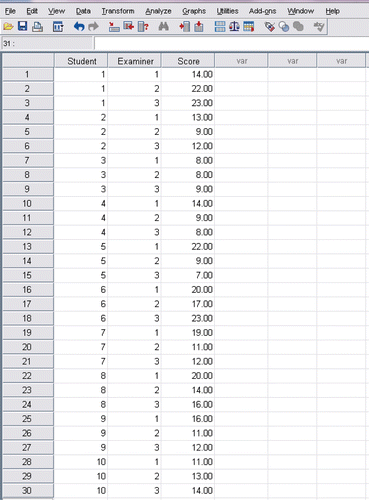
A single facet design examines only a single source of measurement error in a test although in reality others may exist. For example, in an OSCE examination, we might like to focus on the influence of examiners as sources of error. In G-theory, this is called a one-facet ‘student (s) crossed-with-examiner (e)’ design: (s × e). Consider an OSCE in which three examiners independently rate a cohort of clinical students on three different stations using a 1–5 check list of 5 items. The total mark can therefore range from 5 to 25, with higher mark suggesting a greater level of performance in each station. Using G-theory, we can find out what amount of measurement error is generated by the examiners. For illustrative purpose, only 10 students and the three examiners are presented in the Data Editor of SPSS in Figure 4.

Figure 4. Hypothetical scoring of 10 students by three examiners on three different OSCE stations.

Before analysing, the data needs to be restructured. To this end, from the data menu at the top of the screen, one clicks on ‘restructure’ and follows the appropriate instructions. In Figure 5, the restructured data format is presented.

Figure 5. Restructured data from Figure 4.

To obtain the variance components, the following steps are carried out:

From the menus chooses ‘Analyse’, ‘General Linear Model’, respectively. Then click on ‘variance components’. Click on ‘Score’ and then click on the arrow to move ‘Score’ into the box marked ‘dependent variable’. Click on student and examiner to move them into ‘random factors’. After ‘variance estimates’ appears, click OK and the contribution of each source of variance to the result is presented as shown in Table 8.

Table 8.  Results of variance components estimates

Source of variation	Variance component (s × e) design	Percentage variance
Student	10.144	40.00
Examiner	1.578	6.20
Student × examiner	13.656^a	53.80

Note: ^aResidual variance.

Table 8 shows that the estimated variance components associated with student and examiner are 10.144 and 1.578, respectively. Expressed as a percentage of the total variance, it can be seen that 40.00 % is due to the students and 6.20 % to the examiners. However, the variance of the students is not considered a facet of measurement error as this variation is expected within the student cohort and in terms of G-theory, it is called the ‘object of measurement’ (Mushquash & O'Connor 2006). Importantly for our analysis, the findings indicate that the examiners generated 6.20% of the total variability, which is considered a reasonably low value. Higher values would create concern about the effect of the examiners on the test. The residual variance is the amount of variance not attributed to any specific cause but is related to the interaction between the different facets and the object of measurement of the test. In this example, 13.656 or 53.80% of the variance is accounted for by this factor.

On the basis of the findings of Table 8, we are now in a position to calculate the generalisability coefficient. In this case, the G-coefficient is defined as the ratio of the student variance component (denoted ) to the sum of the student variance component and the residual variance (denoted ) divided by the number of examiners (k) (Nunnally and Bernstein 1994) and written as follows:

Inserting the values from above, this gives:

The G-coefficient, traditionally depicted as ρ ², is the counterpart of the well-known reliability coefficient with values ranging from 0 to 1.0. (It is worth noting that the G-coefficient in the single facet design described above is equal to Cronbach's alpha coefficient (for non-dichotomous data) and to Kuder–Richardson 20 (for dichotomous data). The interpretation of the value of the G-coefficient is that it represents the reliability of the test taking into account the multiple sources of error calculated from their variance components. The higher the value of the G-coefficient, the more we can rely on (generalise) the students’ scores and the less influence the study facets have been. In the above example, the G-coefficient has a reasonably high value and the variance component for examiners is low. This shows that the examiners did not have significant variation in scoring students and that we can have confidence in the students’ scores.

A multi-facet design

Clearly in an OSCE examination, there are a number of other potential facets that need to be taken into consideration in addition to the examiners. For example, the number of stations, the number of SPs and the number of items on the OSCE checklist. We will now explain how to calculate the variance components and a G-coefficient for a multi-facet design building on the previous example. Each of three stations now has a SP and a 5-item checklist leading to an overall score for each student. Here, examiners, stations, SPs and items can affect the student performance and hence are facets of measurement error.

However, because we are now interested in the influence of the number items as a source of error, we need to input the score for each item (i), for each student (s), for each station (st), for each SP (sp) and for each examiner (e). After entering exam data into SPSS and restructuring it, analysis of variance components is carried out as described before. Table 9 shows the hypothetical results of variance components for potential sources of measurement error in the OCSE results.

Table 9.  Results of variance components estimates

Source of variation (n)	Variance component s × e × i× sp × st design	Percentage of variance
Student (10)	0.313	15.04
Examiner (3)	0.060	2.88
Item (5)	0.033	1.59
SP (3)	0.000	0.00
Station (3)	0.000	0.00
Student × item	0.096	4.62
Student × examiner	0.341	16.37
Student × item × examiner	1.231	59.16
Item × examiner × station	0.007	0.34

Notes: Residual variances for interactions between facets equal to zero have not been displayed in the table. They have no influence on the test and are redundant.

Table 9 shows that 59.16 %, 16.37 % and 15.04 of the sources of measurement error are generated by interactions between student, item and examiner, interactions between student and examiner and student, respectively. The lack of residual variance between other combinations of facets indicates that student scores cannot fluctuate owing to these interactions and consequently they do not lead to any measurement error. The value for the variance component for examiners (0.06) in Table 9 differs from the value in Table 8 (1.57) because in creating the multi-facet matrix, we are using individual item scores from students rather than their total mark for all stations. These findings also indicate that there is little disagreement about the actual scores given to student by each examiner (2.88%). We can insert the values of the variance components and the numbers associated with each facet shown in Table 8 into the following equation:

Zero values of variance components are not inserted, thus excluding SPs and stations.

In this example, the G-coefficient is high and the variance components of the facets are low, hence the reliability of the OSCE is very good. If higher values of variance components are found for particular facets, then they need to be examined in more detail. This might lead to better training for examiners or modifying items in checklists or the number of stations. Given the high G-coefficient shown with these hypothetical data, we could in principle reduce the values of k for individual facets whilst maintaining a reasonably high value of G and hence maintaining the reliability of the OSCE exam. In the real world of OSCEs, this could lead to simplifications and a reduction in the cost of OSCE examining. As for Cronbach's alpha statistic, there are different views concerning acceptable values for G ranging from 0.7 to 0.95 (Tavakol and Dennick 2011a, b). This ability to manipulate the generalisability equation in order to see how examination factors can influence sources of measurement error and hence reliability lies at the heart of decision study or D-study (Raykov & Marcoulides 2011). Thus G-theory and D-study provide a greater insight into the various processes occurring in examinations, hidden by merely measuring Cronbach's alpha statistic. This enables assessors to improve the quality of assessments in a much more specific and evidence-based way.

The IRT and Rasch modelling

Test constructors have traditionally quantified the reliability of exam tests using the CTT model. For example, they use item analysis (item difficulty and item discrimination), traditional reliability coefficients (e.g. KR-20 or Cronbach's alpha), item-total correlations and factor analysis to examine the reliability of tests. We have just shown how G-theory can be used to make more elaborate analyses of examination conditions with a view to monitoring and improving reliability. CTT focuses on the test and its errors but says little about how student ability interacts with the test and its items (Raykov & Marcoulides 2011). On the other hand, the aim of IRT is to measure the relationship between the student's ability and the item's difficulty level to improve the quality of questions. Analyses of this type can also be used to build up better question banks for Computer Adaptive Testing (CAT).

Consider a student taking an exam in anatomy. The probability that the student can answer item 1 correctly is affected by the student's anatomy ability and the item's difficulty level. If the student has a high level of anatomical knowledge, the probability that he/she will answer the item 1 correctly is high. If an item has a low index of difficulty (i.e. a hard item), the probability that the student will answer the item correctly is low. IRT attempts to analyse these relationships using student test scores plus factors (parameters) such as item difficulty, item discrimination, item fairness, guessing and other student attributes such as gender or year of study. In an IRT analysis, graphs are produced showing the relationship between student ability and the probability of correct item responses, as well as item maps depicting the calibrations of student abilities with the above parameters. Also tables showing ‘fit’ statistics for items and students, to be described later.

A variety of forms of IRT have been introduced. If we wish to look at the relationship between item difficulty and student ability alone, we use the one-parameter logistic IRT (1PL). This is called the Rasch model in honour of the Danish statistician who promoted it in the 1960s. The Rasch model assesses the probability that a student will answer an item correctly given their conceptual ability and the item difficulty. Two-parameter IRT (2PL) or three-parameter IRT (3PL) are also available where further parameters such as item discrimination, item difficulty, gender or year of study can be included. For the purposes of this article, we are going to concentrate on 1PL or Rasch modelling.

In Rasch modelling, the scores of students’ ability and the values of item difficulty are standardised to make interpretation easier. After standardising the mean, student ability level is set to 0 and the SD is set to 1. Similarly, the mean item difficulty level is set to 0 and the SD is set to 1. Therefore, after standardisation a student who receives a mean score of 0 has an average ability for the items being assessed. With a score of 1.5, the student's ability is 1.5, SDs above the mean. Similarly, an item with a difficulty of 0 is considered an average item and an item with a difficulty of 2 is considered to be a hard item. In general, if a value of a given item is positive, that item is difficult for that cohort of students and if the value is negative, that item is easy (Nunnally & Bernstein 1994).

To standardise the student ability and item difficulty, consider Table 10, presenting the simulated dichotomous data for seven items on an anatomy test from seven students showing the student ability for each student and the difficulty level for each of the seven items. To calculate the ability of the student, which is called θ , the natural logarithm of the ratio of the fraction correct to the fraction incorrect (or 1 – fraction correct) for each student is taken. For example, the ability of student 2 (θ₂) is calculated as follows:

This indicates that the ability of student 2 is 0.89 above the mean SD. To calculate the difficulty level of each item which is called b, the natural log of the ratio of the fraction incorrect (or 1 – fraction correct) to the fraction correct for each item is calculated. For example, the difficulty of item 2 is calculated as follows:

A value of −1.73 suggests that the item is relatively easy. This standardisation process is carried out for all students and all items and can easily be facilitated in an Excel spreadsheet (Table 10).

Table 10.  A simulated 7-item test of anatomy ability

Student	Item 1	Item 2	Item 3	Item 4	Item 5	Item 6	Item 7	FC^a	SA^b (θ)
1	1	0	0	0	1	0	1	0.43	−0.28
2	1	1	1	1	0	1	1	0.71	0.90
3	1	1	1	0	1	0	0	0.57	0.28
4	1	0	1	0	1	0	1	0.57	0.28
5	0	0	0	0	0	0	1	0.14	−1.82
6	1	0	1	1	1	0	0	0.57	0.28
7	1	0	0	1	1	0	0	0.43	−0.28
FC^a	0.85	0.28	0.57	0.43	0.71	0.14	0.57
ID^c (b)	−1.73	0.90	−0.28	0.28	−0.89	1.80	−0.28

Note: ^aFraction correct, ^bstudent ability and ^citem difficulty.

Table 11.  Estimates of the probability of answering the correct answer for item 1

Student	b	θ	p
1	−1.73	−0.28	0.81
2	−1.73	0.90	0.93
3	−1.73	0.28	0.88
4	−1.73	0.28	0.88
5	−1.73	−1.82	0.48
6	−1.73	0.28	0.88
7	−1.73	−0.28	0.81

We are now in a position to estimate the probability that a student with a specific ability will correctly answer a question with a specific item difficulty. For 1PL, the following equation is used to estimate the probability:

Where p is the probability, θ is the student ability and b the item difficulty. Referring to Table 10, the ability of student 1 is −0.28 SD below the average, and item 1, with a difficulty level of −1.73, was answered correctly, which is below the average. On the basis of the above formula, the probability that student 1 will answer item 1 correctly is [1/(1 + e^{−(−0.28−(−1.73))}] = 0.12. Considering student 3's ability level and the difficulty of item 4, the probability that the student will answer correctly item 3 is [1/(1 + e^{−(0.28−(0.28))}] = [1/(1 + e⁰)] = 0.50. This shows that if the level of student ability and the level of item difficulty are matched, the probability that the student will select the correct answer is 50%, which is equal to chance. The fundamental aim of Rasch analysis is to create test items that match their degree of difficulty with student ability. In simple terms, the ‘cleverness’ of the students should be matched with the ‘cleverness’ of the items. In order to further examine the relationship between student ability and item difficulty, the data in Table 11 shows the probability (p) that a student will answer item 1, with item difficulty (b), correctly given their ability (θ) using data taken from Table 10 and using the equation above.

Item characteristic curves

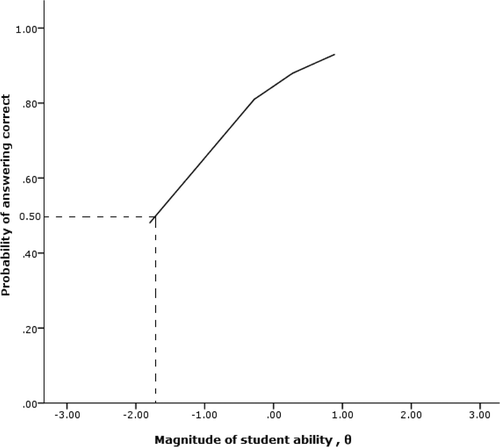
In Rasch analysis, the relationship between item difficulty and student ability is depicted graphically in an item characteristic curve (ICC) shown in Figure 6.

Figure 6. ICC for item 1 from Table 10.

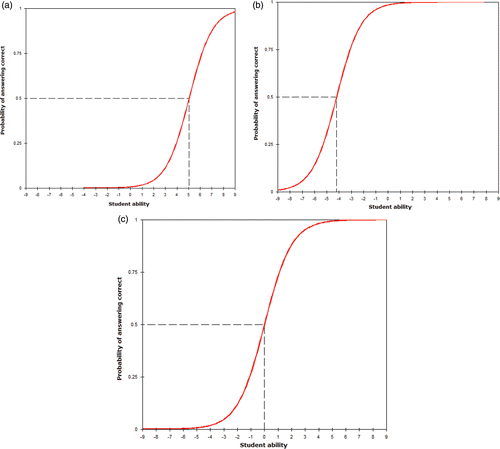
In Figure 6, dotted lines are drawn to interpret the characteristics of item 1. There is a 50% probability that students with an ability of −1.85 will answer this question correctly. This implies that student with lower ability have an equal chance of answering this question correctly. In addition, a student with an average ability (θ = 0) has an 80% chance of giving a correct answer. The implication is that this question is too easy. It should be noted that if an item shifts the curve to the left along the theta axis, it will be an easy item and a hard item will shift the curve to right. Examples of ICC curves for items taken from an examination analysis shown in Figure 8 are displayed in Figure 7. Figure 7(a) shows a difficult question (Question 101) and Figure 7(b) shows an easy question (Question 3). Figure 7(c) shows the ‘perfect’ question (Question 46) in which students of average ability have a 50% chance of giving the correct answer.

Figure 7. Examples of the ICC.

Figure 8. ISM; each '#' represents four students and ‘.’ represents one student.

Item-student maps

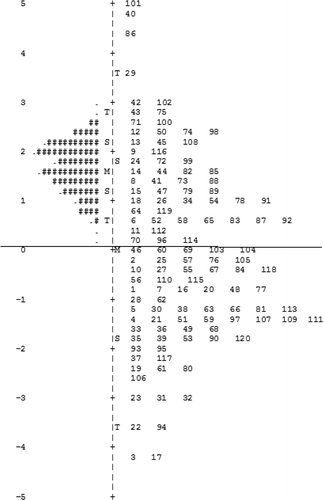
The distribution of students’ ability and the difficulty of each item can also be presented on an Item–student map (ISM). Using IRT software programmes such as Winsteps® (Linacre, 2011) item difficulty and student ability can be calculated and displayed together. Figure 8 shows the ISM using data from a knowledge-based test. The map is split into two sides. The left side indicates the ability of students whereas the right side shows the difficulty of each item. The ability of each student is represented by ‘hash’ (#) and ‘dot’ (.), items are shown by their item number. Item difficulty and student ability values are transformed mathematically, using natural logarithms, into an interval scale whose units of measurement are termed ‘logits’. With a logit scale, differences between values can be quantified and equal distances on the scale are of equal size (Bond & Fox 2007). Higher values on the scale imply both greater item difficulty and greater student ability. The letters of ‘M’, ‘S’ and ‘T’ represents mean, one standard deviation and two standard deviations of item difficulty and student ability, respectively. The mean of item difficulty is set to 0. Therefore, for example, items 46, 18 and 28 have an item difficulty of 0, 1, and −1 respectively. A student with an ability of 0 logits has a 50% chance of answering items 46, 60 or 69 correctly. The same student has a greater than 50% probability of correctly answering items less difficult, for example items 28 and 62. In addition, the same student has a less than 50% probability of correctly answering more difficult items such items 64 and 119.

By looking at the ISM in Figure 8 we can now interpret the properties of the test. First, the student distribution shows that the ability of students is above the average, whereas more than half of the items have difficulties below the average. Second, the students on the upper left side are ‘cleverer’ than the items on the lower right side meaning that the items were easy and unchallenging. Third, most students are located opposite items to which they are well matched on the upper right and there are no students on the lower left side. However, items 101, 40, 86 and 29 are too difficult and beyond the ability of most students.

Overall, in this example, the students are ‘cleverer’ than most of the items. Many items in the lower right hand quadrant are too easy and should be examined, modified or deleted from the test. Similarly, some items are clearly too difficult. The advantage of Rasch analysis is that it produces a variety of data displays encapsulating both student and item characteristics that enable test developers to improve the psychometric properties of items. By matching items to student ability, we can improve the authenticity and validity of items and develop higher quality item banks, useful for the future of computer adapted testing.

Conclusions

Objective tests as well as OSCE stations should be the psychometrically sound instruments used for measuring the proficiency of students and can be of use to medical educators interested in the actual use of these examination tests in the future. In this Guide, we tried to simply explain how to interpret the outcomes of psychometric values in objective test data. Examination tests should be standardised both nationally and locally and we need to ensure about the psychometric soundness of these tests. A normal question that may be posed is to what extent our exam data measure the student ability (to what extent the students have learned subject matter). The interpretation of exam data using psychometric methods is central to understand students’ competencies on a subject matter and to identify students with low ability. Furthermore, these methods can be employed for test validation research. We would suggest medical teachers, especially who are not trained in psychometric methods, practice these methods on hypothetical data and then analyse their own real exam data in order to improve the quality of exam data.

Summary

This Guide has explained the interpretation of post-examination interpretation of objective test data. There are a number of psychometric methods for determining the validity and reliability of tests. CTT enables medical educators to detect abnormal items on a test and to identify systematic errors that may have influenced the student ability on a test. Factor analysis allows medical educators to reduce the irrelevant items, and to hypothesise relationships within items and constructs (factors) associated with student competence. We introduced CFA and structural equation modelling to test hypotheses about the relationship between items and constructs (the underlying internal structure of the test). Although Cronbach's alpha is traditionally used as an estimation of the reliability of a test, it does not assess a combination of source of measurement error that exists in observed scores of students on a test. Using Generalisability study, medical educators can show the exact position of error and then isolate it in order to estimate variance in each source of measurement error. SPSS is used for measuring sources of measurement errors to calculate G-coefficient. One of the limitations of CTT is that it does not provide the opportunity to measure how students of different ability on a particular test perform on a particular item. IRT using Rasch modelling can address the relationship between the item ability and student ability from a set of the student cohort. Using IRT, medical educators will be able to evaluate the psychometric features of existing examination tests and to remove anomalies in items. Using IRT will also employ to develop item banking in which turn leads to CAT.

Declaration of interest: The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the article.