Abstract
This paper presents the mechanical quadrature methods (MQMs) for solving the boundary integral equations of steady-state anisotropic heat conduction equation on the smooth domains and polygons, respectively. The costless and high-accurate Sidi–Israeli quadrature formula are applied to deal with the integrals in which the kernels have a logarithmic singularity. Especially, the Sidi transformation is used for the polygon cases in order to obtain a rapid convergence by degrading the singularity at the corners on the boundary. The convergence and stability of the MQMs solution are proved based on Anselone's collective compact theory. In addition, asymptotic error expansion of the MQMs shows that the approximation order is of O(h3), where h is the partition size of the boundary. Finally, numerical examples are tested and results verify the theoretical analysis.
1. Introduction
Materials in which the thermal conductivity varies in different directions are called anisotropic materials. For example, crystals, wood, sedimentary rocks, metals that have undergone heavy cold pressing, fibre reinforced structures, and many others are anisotropic materials. Therefore, the study of heat conduction in anisotropic materials has numerous important applications in various branches of science and engineering Citation20,Citation21,Citation25.
Consider the direct, well-posed interior Dirichlet problem, which consists of the solution of the steady-state heat conduction equation subject to the specification of the temperature over the whole boundary, i.e. the problem to be solved is
Obviously, the solution to problems governed by EquationEquation (1) is a complicated process. In the case of orthotropy, where the cross-derivative term is absent, the analysis can be considerably simplified. Hence, a conventional way to numerically treat the fully anisotropic problem is transform EquationEquation (1) into the ‘orthotropic’ form: after the rotation of the original Cartesian axes to the principal axes, ◯1 and ◯2, the cross-derivative term disappears. Thus, EquationEquation (1) takes the form of
In this paper, we directly apply the fundamental solution of EquationEquation (1) to solve the two-dimensional anisotropic field problems without domain deformation and rotation. As we all known, the indirect BEMs can be used to construct the solution for the two-dimensional Dirichlet problem Equation(1): the unknown function φ can be represented as a single-layer potential of the form
The kernels of Equation(4) have singularities at the points x=y, which degrade the rate of convergence. For applications in BEM, some classical numerical methods can be used to overcome this difficulty, such as the Galerkin boundary method (GM) in Stephan and Wendland Citation30, Sloan and Spence Citation29, the quadrature method in Saranen Citation22Citation23, and the collocation method (CM) in Costabel et al. Citation9. However, these methods do not provide a good accuracy in the solution near the singular points. For example, the accuracy of Galerkin methods Citation29 is only O (hτ) (0<τ<2) and the accuracy of collocation methods Citation31 is even lower.
In this article, the mechanical quadrature methods (MQMs) are proposed to calculate weakly singular integrals by Sidi–Israeli quadrature formula Citation28. The associated convergence and stability analysis are given, which show that the quadrature formula in the MQMs are simpler than the analytical formula in Citation25, and the MQMs possess the optimal condition number and retain the optimal convergence rate.
This paper is organized as follows: in Section 2, the convergence and error bound analysis are carried out based on the theory of collectively compact operators Citation1Citation2 for closed smooth boundaries and closed curved polygons, respectively. The error and stability analysis are given in Section 3. Numerical examples are provided to verify the theoretical results in Section 4, and some useful conclusions are made in Section 5.
2. Mechanical quadrature methods
2.1 Closed smooth curve Γ
Assume that CΓ≠1 and Γ be parameterized by x(t)=(x1(t), x2(t)):[0, 2π]→Γ, with , where μ̄ and μ are two constants. Let C˜ℓ[0, 2π] consist of periodic functions with period 2π, which has derivatives up to 2ℓ, i.e. v∈C˜ℓ[0, 2π]={v(t)|v(μ)(t)∈C[0, 2π], v(μ)(t+2π)=v(μ)(t), μ=0, 1, …, 2ℓ}.
Define the integral operator
The integral operator Kw can be split into a singularity part and a compact perturbation part as follows
For the logarithmically singular operator A, the associated integral is needed to be evaluated by means of Cauchy Principal Value. High accuracy for numerical computation of finite-range integrals with weakly singular kernels can be achieved by Sidi–Israeli quadrature formula. Now, we describe the Sidi–Israeli quadrature formula for weakly singular integrals. Let
Let τj=jh (j=0, 1, …, n). From the representation of a(t, τ), we know H1(t, τ)=−1/2π and H2(t, τ)=1/4π. Thus, we can construct the Fredholm approximation of A,
which has the following error bounds:
For the integral operators B with periodic kernels, we can construct the Nyström approximation by the trapezoidal rule Citation12. The Nyström approximate operator Bh of B can be defined as:
From EquationEquation (9), we have
In order to prove the existence and convergence of numerical approximations, we first introduce two special operators. Let Vh=span{ej(t), j=0, 1, …, n}⊂C[0, 2π) be a piecewise linear function subspace with nodes , where ej(t) is the basis function satisfying ej(ti)=δji. Define a prolongation operator
satisfying
, and a restricted operator
satisfying
.
Lemma 2.1
The operator sequence {Ih(Ah)−1RhAh:C3[0, 2π)→C[0, 2π)} is uniformly bounded and convergent to the embedding operator I.
Proof
Let ω∈C3[0, 1] and ωh be solutions of auxiliary equations Aω=η and Ahωh=Rhη, respectively, where η∈C4[0, 1]. By using Sidi–Israeli quadrature formula, we have
where
Now we give two concepts, which can be seen in Citation3Citation4. Let denote the closed unit ball in X. Then
is collectively compact if and only if the set
has compact closure in Y. Define collectively compact convergence
:
Lemma 2.2
Let the integral operator and A−1 exist, and let the integral operator
Cr+1[0, 2π)) with the kernel b(t, τ) of B satisfy A−1b(., τ)=b̄(t, τ), where
is a linear bound operator space. Also assume that b̄(t, τ) and (∂/∂ t)b̄(t, τ) are continuous on [0, 2π)2. Let τj=(j−1)h (j=1, …, n) be nodes. Then the Nyström approximation of B̄,
Proof
From EquationEquation (15), we have
Corollary 2.3
For an integral operator B with a periodic smooth kernel b(t, τ), defining the Nyström approximation
Proof
Because the kernel b(t, τ) of the operator B and its derivatives of higher order are continuous Citation5, and we have
Replacing (Ah)−1, Ah, and Bh by (Âh)−1=Ih(Ah)−1Rh, Âh=Ih(Ah)Rh and Bˆh=IhBhRh, respectively. Consider the operator equation
Theorem 2.4
The operator sequence {(Âh)−1Bˆh} is collectively compact convergent to A−1B in C[0, 2π), i.e.
Proof
Let {χh}h∈H be a bounded sequence, where χh={xh}, and hj→0 as j→∞. Consider the convergence of
2.2 Closed curved polygons Γ
Let be the boundary of a polygonal domain Ω in ℝ2 with CΓ≠1, Γm∈C2ℓ+1(m=1, …, d, ℓ∈N), and let
. Define the boundary integral operators on Γm,
Then EquationEquation (4) can be converted into a matrix operator equation
Sidi transformation in using the trapezoidal rule to evaluate was proposed in Citation26, where h(x) is not necessarily continuous or differentiable at x=0 and x=1, and h(x) may even behave singularity at the endpoints with different types of singularities. Let the variable transformation ψγ(t) have the property that
Now we give the following decomposition of Klm, namely,
The operator All is defined on the circular contour with radius e−1/2. From Citation32Citation29, we have
Let P1, …, Pd denote the corner points of the boundary Γ. Define a function χm∈[−1, 1]
Since the boundary Γ is closed polygon, the solution singularity for EquationEquation (26) occurs at the corner points P1, …, Pd of the boundary Γ Citation5Citation29Citation32. The solution wm(x)=∂ φm(x)/∂ ν−−∂ φm(x)/∂ ν+ has a singularity when s=sm, where βm=−|χm|/(1+|χm|), βm∈[−½, 0) and sm denotes the arc parameter at Pm.
Lemma 2.5 Citation17
(1) Suppose that the function
where βm∈[−½, 0) and hm(s)∈C∞[0, 1 with hm(0)≠0. Then the function wm(t) can be expressed by
where c1 and c2 are two constants independent of t.(2) Suppose that the function
where βm∈[−½, 0) and h˜m(s)∈C∞[0, 1] with h˜mEquation(1)≠0. Then the function wm(t) can be expressed by
where c3 and c4 are two constants independent of t.
Proof
(1) By using Taylor's formula, we can obtain
andBy substituting EquationEquations (30) and Equation(31) into the expression of wm(t), we obtain EquationEquation (28). The proof for Equation(2) of Lemma 2.5 is similar.
By Lemma 2.5 and βm≥−½, we can obtain (γ+1)(βm+1)−1≥0 for γ≥1. Hence, we have the following remark.
Remark 1 Although vm(s) has singularities at endpoints s=0 and s=1, wm(t) has no singularity by Sidi transformation at t=0 and t=1.
Bellow we study singularity for the kernels blm(t, τ) (l, m=1, …, d). Obviously, if Γl∩Γm=∅, blm(t, τ) are continuous in [0, 1]2, and if Γl∩Γm≠∅, blm(t, τ) have singularities at the points (t, τ)=(0, 1) and (t, τ)=(1, 0). For convenience of analysis, we only discuss the case in which (t, τ)=(1, 0). Defining the following function
Lemma 2.6
Let b˜lm(t, τ) be defined by Equation Equation(32), then b˜lm(t, τ) and (∂kb˜lm(t, τ)/∂ τk) (k=1, 2) are smooth on [0, 1]2.
Proof
By using the continuity of b˜ll(t, τ) and the boundness of sin γ(π t), we can immediately complete the proof for the case l=m. Let Γl−1∩Γl=Pl=(0, 0) and θl∈(0, 2π) is the corresponding interior angle. Then we have
Remark 2 The kernel blm of Blm(t, τ) has singularities at corners (t, τ)=(0, 1) and (t, τ)=(1, 0), but sinγ(π t)blm(t, τ) has no singularities.
Let hm=(1/nm) (nm∈N, m=1, …, d) and tmj=τmj=(j−1/2)hm (j=1, …, nm) be the step sizes and boundary nodes, respectively. The trapezoidal rule approximation for the boundary integral operator Blm is
Letting t=tli (l=1, …, d, i=1, …, nl), we have the discrete equations of Equation(26)
EquationEquation (38) has n () unknowns. Once Wh is solved from EquationEquation (38), the solution φ(y) (y∈Ω) can be calculated by
From EquationEquations (37) and Equation(39), we can obtain the circulate matrix
For the properties of , we have the following lemma.
Lemma 2.7 Citation15Citation17
\
Equation(1) Let λlk (k=1, …, nl; l=1, …, d) be the eigenvalues of
. Then there holds
where c1 and c2 are two positive constants.(2)
and Ah are invertible, and the following holds
where hmin=min 1≤l≤dhl and ‖·‖ denotes the spectral norm.
Let C0[0, 1]={g(t)∈C[0, 1]:g(t)/sin γ(π t)∈C[0, 1]} denote the subspace of the space C[0, 1] with the associated norm ||g||*=max 0≤t≤1|g(t)/sin γ(π t)|, and also let span{Nmj(t), j=1, …, nm}⊂C0[0, 1] be a piecewise linear function subspace with the basis nodes
, where Nmj(t) are the basis functions satisfying Nmj(tmi)=δji. Define a prolongation operator
satisfying
for all
, and a restricted operator
satisfying
for all gm∈C0[0, 1].
Lemma 2.8
Suppose that satisfy CΓ≠1. Then there exists a constant M1 independent of hl such that
Proof
From Citation17, the operator sequence is uniformly bounded and convergent to the embedding operator I. Hence, the proof of Lemma 2.8 is completed. ▪
Lemma 2.9 Citation14
Let the integral operator and
exist, and let the integral operator
with the kernel lm(t, τ) of Lm satisfy
where
is a linear bound operator space, and l̄m is the kernel of L̄m. Also assume that l̄m(t, τ) and (∂/∂ t)l̄m(t, τ) are continuous on [0, 1]2. Let τm=(m−½)hl (j=1, …, nm) be nodes. Then the Nyström approximation of L̄j,
Corollary 2.10
\
Equation(1) For Γm=Γl or Γm∩Γl=∅, let
be the Nystr öm's approximation of Blm, and also let blm be the kernel of the integral operator Blm. Then under the transformation Equation(23), there holds
where M2 is a constant independent of hm.(2) For Γm∩Γl∈{Pm}, let
be the approximation of B˜lm, and also let b˜lm=sinγ(πτ) be the kernel of integral
. Then under the transformation Equation(23), there exists a constant M3 independent of hm such that
Proof
(1) Since |l−m|≠1 or d−1, by the definition of Blm we know the kernel blm(t, τ) of the operator Blm and its derivatives of higher order are continuous. By Lemma 2.9, we have
which implies that the sequenceis uniformly bounded. The proof is completed.
(2) From Lemma 2.6, we know that b˜lm(t, τ) are continuous on (C2[0, 1])2. Hence, the proof for Equation(2) of Corollary 2.10 is similar to the proof for Equation(1).
Lemma 2.11 Citation17
Under the same conditions of Corollary 2.10, by the trapezoidal or the midpoint rule, we have
Proof
Using the results of Lemma 2.8 and Corollary 2.10, we have
and
Using and
to replace
and
(m, l=1, …, d), respectively. Define an operator (Âh)−1Bˆh: (
, where (Âh)−1Bˆh=Ih (Ah)−1RhBh,
and
. Then the associated equation of EquationEquation (38) is
Theorem 2.12 Citation13
Assume that there exists a unique solution in Equation Equation(4), and Γm∈C2ℓ+1 (m=1, …, d, ℓ∈N). Then the operator sequence {(Âh)−1Bˆh} is collectively compact convergent to A−1B in the space V=(C0[0.1])d. That is, the following holds
Proof
Let Θ={z:||z||≤1, z∈(C[0, 1])d} be the unit ball in the space V, and
3. Errors and stability analysis for MQMs
3.1 Errors analysis for MQMs
In the case of closed smooth boundary Γ, we have the single parameter asymptotic expansions of the solution errors.
Theorem 3.1
If there exists a unique solution in Equation Equation(4), f̄, f̄h are computed by Equations Equation(8) and Equation(12), respectively, xi∈C6[0, 2π) (i=1, 2) and f(s)∈C5[0, 2π), then there exists a function ϱ∈C5[0, 2π) independent of h such that
Proof
By the midpoint trapezoidal rule, the asymptotic expansion holds Citation13Citation14
Define the auxiliary equation
Similar to Theorem 3.1, we have the following theorem in the case of closed curved polygon Γ.
Theorem 3.2 Citation16
Let the boundary satisfy CΓ≠1 and suppose
. Then there exists functions ϱm∈C0[0, 1] (m=1, …, d) independent of hm (m=1, …, d) such that the following multi-parameter asymptotic expansions hold at nodes, provided ωm(γ+1)>3 (m=1, …, d) for γ≥1,
Furthermore, we have
3.2 Stability analysis for MQMs
For simplicity, we give the stability of MQMs for smooth boundary and polygon together.
Theorem 3.3 Citation15Citation17
Suppose that satisfy CΓ≠1. When d=1, the boundary Γ (=Γ1) is a smooth and closed curve, and when d>1, the boundary
is a closed polygon, and Γm (m=1, …, d) be smooth curves. Suppose that Ah̄ and Bh̄ are the discrete matrices defined by Equations Equation(9) and Equation(11), or Equation(38), respectively, where h̄=h when d=1, and h̄=hmin =min 1≤m≤dhm when d>1. Here, h and hm (=1/nm, m=1, …, d) is the mesh step size of the smooth curve and the curved edge Γm, respectively. Then there exists two positive constants ĉ1 and ĉ2 independent of h̄ such that
where λi (i=1, …, nm) are the eigenvalues of discrete matrix Kh̄=|κij|1/2(Ah̄+Bh̄). In addition, the following hold
The proof of Theorem 3.3 is similar to the proof of Theorem 3.4 in Citation17.
4. Numerical examples
In this section, to verify theoretical results in this paper, we present two numerical examples for the steady-state anisotropic heat conduction problems by MQMs.
Let en=|φ−φn| be the errors by MQMs using n boundary nodes, and let rn=en/en/2 be the error ratio by MQMs, where n=2π/h.
Example 1
Citation21 Let us consider the steady-state heat transfer in an anisotropic material in the plane domain , i.e. the two dimensional disc of radius unity. The thermal conductivity tensor κij are given by κ11=5.0, κ12=κ21=2.0, and κ22=1.0. The analytical solution is
.
Let the boundary of be divided into n (=2k, k=4, …, 10) sections. We compute the numerical solution φ of the interior points in the subregion
,
, where
,
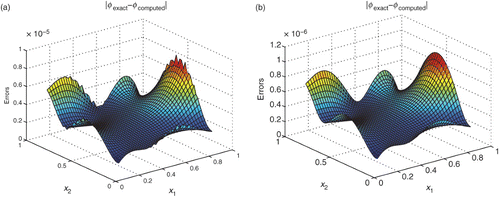
, N1=20, and N2=100}. The subregion Ω1 is shown in . shows the errors at a series of points along the line x1=x2 when n=29 and n=210, respectively. The associated errors of φ and corresponding isoline plots of the errors in Ω1 are shown in and , respectively.
Figure 2. (a) Errors of temperature by 29 boundary nodes; (b) errors of temperature by 210 boundary nodes.
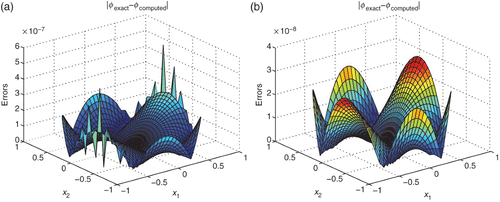
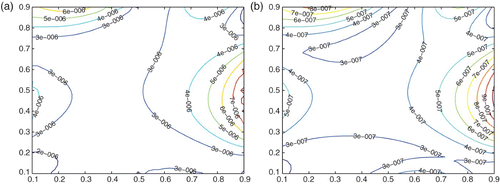
Figure 3. (a) Isolines of errors of temperature by 29 boundary nodes; (b) isolines of errors of temperature by 210 boundary nodes.
The computational errors and error ratio at the interior points (0.1, 0.1), (0.25, 0.25) and (0.5, 0.5) using n (=2k, k=4, …, 10) nodes by MQMs are listed, respectively, in . From the numerical results we can see that log 2rn≈ 3, which means that the convergence rates of φ are O (h3) for MQMs. In the condition number |λmin| and |λmax| of eigenvalues λi (i=1, …, n) for the matrix Kh=|κij|1/2(Ah+Bh) are provided. From , we can see to indicate Equation(65). It verifies the stability of the convergent theory about φ.
Table 1. The condition number for κ11=5.0, κ12=2.0, κ12=1.0.
Table 2. The errors of φ at the point (0.1, 0.1).
Table 3. The errors of φ at the point (0.25, 0.25).
Table 4. The errors of φ at the point (0.5, 0.5).
Example 2 Let the boundary denote the boundary of the rectangle Ω, where Γ1={(x1, 0): 0≤x1≤1}, Γ2={(1, x2): 0≤x2≤1}, Γ3={(x1, 1):0≤x1≤1}, and Γ4={(0, x2): 0≤x2≤1}. The thermal conductivity tensor is given by κ11=1, κ12=0.5, and κ22=1. The Dirichlet conditions of EquationEquation (1) were prescribed on the boundary defined by
,
,
, and
. The analytical solution to this problem is
. Let each boundary Γm (m=1, …, 4) be divided into 2k (k=3, …, 7) segments. We compute the numerical solution φ of the interior points using ψ6 transformation in the subregion
. From EquationEquation (23), we know ψ6(t)=(60π t−45 sin (2π t)+9 sin (4π t)−sin (6π t))/(60π), where t∈[0, 1]. The ψ6 transformation and Ω2 are shown in , respectively.
Let Λk denote (2k, 2k, 2k, 2k), where (2k, 2k, 2k, 2k) (k=4, …, 7) represents the number of boundary nodes on (Γ1, Γ2, Γ3, Γ4). The errors and error ratio of the interior points (0.1, 0.1), (0.2, 0.2) and (0.6, 0.6) using n (=4×2k, k=3, …, 7) nodes by MQMs are listed in , respectively. From the numerical results we can see that log 2rn≈ 3, which means that the convergence rates of φ are O (h3) for MQMs. In the condition number, |λmin|, and |λmax| of eigenvalues λi (i=1, …, n) for the matrix Kh=|κij|1/2(Ah+Bh) are provided. From , we can see , which verifies the stability of the convergent theory about φ.
Table 5. The condition number for κ11=1.0, κ12=0.5, κ12=1.0.
Table 6. The errors of φ at the point (0.1, 0.1).
Table 7. The errors of φ at the point (0.2, 0.2).
Table 8. The errors of φ at the point (0.6, 0.6).
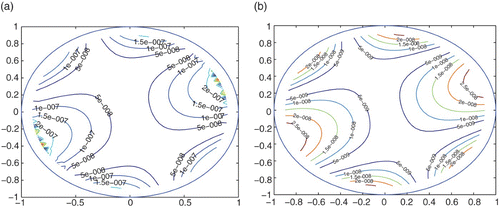
shows the errors at a series of points approaching the corner point (0, 0) along the line x1=x2. and show the errors of φ in Ω2 when 4×2k (k=4, …, 7) boundary nodes used by MQMs. and show the isolines of the errors of φ in Ω2 using 4×2k (k=4, …, 7) boundary nodes by MQMs.
Figure 6. (a) Errors of temperature by 4×24 boundary nodes; (b) errors of temperature by 4×25 boundary nodes for Example 2.
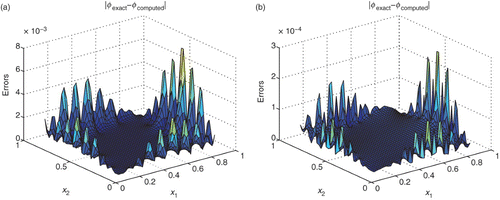
Figure 7. (a) Errors of temperature by 4×26 boundary nodes; (b) errors of temperature by 4×27 boundary nodes for Example 2.
5. Conclusions
In this paper, the convergence and stability of MQMs for the first kind integral equations of steady-state anisotropic heat conduction problems are studied. Problems on the 2D domain with smooth boundaries and polygons are considered, respectively. The numerical results show that the rate of error convergence for the prosed MQMs is O (h3), which matches our theoretical analysis. Furthermore, the excellent stability of the MQMs has been presented, which shows the condition number of the discrete system of the weakly singularity problems is of the order O (h̄−1).
Acknowledgements
The work was supported by the National Natural Science Foundation of China (10871034).
References
- P.M. Anselone, Collectively Compact Operator Approximation Theory, Prentice-Hall, Englewood Cliffs, NJ, 1971.
- P.M. Anselone, Singularity subtraction in numerical solution of integral equations, J. Aust. Math. Soc. 22 (1981), pp. 408–418. doi: 10.1017/S0334270000002757
- P.M. Anselone and T.W. Palmer, Collectively compact sets of linear operators, Pacific J. Math. 25 (1968), pp. 417–422. doi: 10.2140/pjm.1968.25.417
- P.M. Anselone and M.L. Treuden, Regular operator approximation theory, Pacific J. Math. 120 (1985), pp. 257–268. doi: 10.2140/pjm.1985.120.257
- K. Atkinson, The Numerical Solution of Integral Equations of the Second Kind, Cambridge University Press, Cambridge, 1997.
- P.K. Banerjee and R. Butterfield, Boundary Element Methods in Engineering Science, McGraw Hill, Maidenhead, 1981.
- Y.P. Chang, C.S. Kang, and D.J. Chen, The use of fundamental Green's functions for the solution of heat conduction in anisotropic media, Int. J. Heat Mass. Transf. 16 (1973), pp. 1905–1908. doi: 10.1016/0017-9310(73)90208-1
- F. Chatelin, Spectral Approximation of Linear Operator, Academic Press, New York, 1983.
- M. Costabel, V.J. Ervin, and E.P. Stephan, On the convergence of collocation methods for Symm's integral equation on open curves, Math. Comp. 51 (1988), pp. 167–179.
- D. David, Sigmoidal transformations and the trapezoidal rule, J. Aust. Math. Soc. B 40 (1998), pp. 77–137.
- P. Davis, Circulant Matrices, John Wiley and Sons, New York, 1979.
- P. Davis, Methods of Numerical Integration, 2nd ed., Academic Press, New York, 1984.
- J. Huang and T. Lü, The mechanical quadrature methods and their extrapolation for solving BIE of Steklov eigenvalue problems, J. Comput. Math. 22 (2004), pp. 719–726.
- J. Huang and Z. Wang, Extrapolation algorithms for solving mixed boundary integral equations of the Helmholtz equation by mechanical quadrature methods, SIAM J. Sci. Comput. 31 (2009), pp. 4115–4129. doi: 10.1137/080740763
- J. Huang, H.-T. Huang, Z.-C. Li, and Y.M. Wei, Stability analysis via condition number and effective condition number for the first kind boundary integral equations by advanced quadrature methods, a comparison, Eng. Anal. Bound. Elem. 25 (2010), pp. 115–128.
- J. Huang, Z.-C. Li, I.-L. Chen, and H.D.C. Alexander, Advanced quadrature methods and splitting extrapolation algorithms for first kind boundary integral equations of Laplace's equation with discontinuity solutions, Eng. Anal. Bound. Elem. 34 (2010), pp. 1003–1008. doi: 10.1016/j.enganabound.2010.07.004
- J. Huang, G. Zeng, X.-M. He, and Z.-C. Li, Splitting extrapolation algorithm for first kind boundary integral equations with singularities by mechanical quadrature methods, Adv. Comput. Math. 36 (2012), pp. 79–97. doi: 10.1007/s10444-011-9181-8
- R. Kress, Linear Integral Equations, Springer-Verlag, Berlin, 1989.
- W.H. Li, Fluid Mechanics in Water Resources Engineering, Allyn and Bacon, Toronto, 1983.
- N.S. Mera, L. Elliott, D.B. Ingham, and D. Lesnic, An iterative bem for the cauchy steady state heat conduction problem in an anisotropic medium with unknown thermal conductivity tensor, Inv. Probl. Eng. 8 (2000), pp. 579–607. doi: 10.1080/174159700088027748
- N.S. Mera, L. Elliott, D.B. Ingham, and D. Lesnic, A comparison of boundary element method formulations for steady state anisotropic heat conduction problems, Eng. Anal. Bound. Elem. 25 (2001), pp. 115–128. doi: 10.1016/S0955-7997(00)00050-3
- J. Saranen, The modified quadrature method for logarithmic-kernel integral equations on closed curves, J. Int. Equ. Appl. 3 (1991), pp. 575–600. doi: 10.1216/jiea/1181075650
- J. Saranen and I. Sloan, Quadrature methods for logarithmic-kernel integral equations on closed curves, IMA J. Numer. Anal. 12 (1992), pp. 167–187. doi: 10.1093/imanum/12.2.167
- L.J. Segerlind, Applied Finite Element Analysis, John Wiley, New York, 1984.
- Y.C. Shiah and C.L. Tan, BEM treatment of two-dimensional anisotropic field problems by direct domain mapping, Eng. Anal. Bound. Elem. 20 (1997), pp. 347–351. doi: 10.1016/S0955-7997(97)00103-3
- A. Sidi, A new variable transformation for numerical integration, Int. Ser. Numer. Math. 112 (1993), pp. 359–373.
- A. Sidi, Exitension of a class of periodizing variable transformations for numerical integration, Math. Comp. 75 (2005), pp. 327–343. doi: 10.1090/S0025-5718-05-01773-4
- A. Sidi and M. Israeli, Quadrature methods for periodic singular and weakly singular Fredholm integral equation, J. Sci. Comput. 3 (1988), pp. 201–231. doi: 10.1007/BF01061258
- I.H. Sloan and A. Spence, The Galerkin method for integral equations of first-kind with logarithmic kernel: theory, IMA J. Numer. Anal. 8 (1988), pp. 105–122. doi: 10.1093/imanum/8.1.105
- E.P. Stephan and W.L. Wendland, An augmented Galerkin procedure for the boundary integral method applied to two-dimensional screen and crack problems, Appl. Anal. 18 (1984), pp. 183–219. doi: 10.1080/00036818408839520
- Y. Yan, The collocation method for first-kind boundary integral equations on polygonal regions, Math. Comp. 54 (1990), pp. 139–154. doi: 10.1090/S0025-5718-1990-0995213-6
- Y. Yan and I. Sloan, On integral equations of the first kind with logarithmic kernels, J. Int. Equ. Appl. 1 (1988), pp. 517–548. doi: 10.1216/JIE-1988-1-4-517
- J.-J. Zhang, C.L. Tan, and F.F. Afagh, A general exact transformation of body-force volume integral in BEM for 2D anisotropic elasticity, Comput. Mech. 19 (1996), pp. 1–10. doi: 10.1007/BF02757779
- O.C. Zienkiewicz, The Finite Element Method, McGraw Hill, Maidenhead, 1977.