Abstract
We study a special case of the GARCH-in-Mean model proposed by Christensen et al. (Citation2012), where a different specification for the conditional variance was adopted as compared to the traditional GARCH-M model. The conditions about geometric ergodicity are discussed and by checking the conditions of Lemma A.1 in Jensen and Rahbek (Citation2004), the asymptotic normality of the quasi maximum likelihood estimators for the model is established. Simulations demonstrate that the estimation procedure performs well and the given empirical studies indicate the considered model can have comparable performance in data modeling as compared to the standard one.
Mathematics Subject Classification:
1. Introduction
GARCH-in-Mean models have been extensively studied since they were proposed by Engle et al. (Citation1987), which can be generally described as
To be exact, we consider the following model:
This article is arranged as follows. In Sec. 2, we discuss the geometric ergodicity and the asymptotic normality of the QMLE for the considered model. Simulations and empirical studies are shown in Sec. 3. We conclude the article in Sec. 4 and the proofs are put in the Appendix.
2. Ergodicity and Estimation
2.1. Geometric Ergodicity
Putting , then we can reformulate (Equation1.2) and (Equation1.3) as
Recall e t is an independent and identically distributed process with mean 0 and variance 1, and e t is independent of (y s , σ s ), s < t. Define z t = (y t , σ t ), with y t being Y t and σ t being X t , then we can consider (Equation2.1) and (Equation2.2) as special cases of Eqs. (4) and (5) in Meitz and Saikkonen (Citation2008), respectively. According to Proposition 1 in Meitz and Saikkonen (Citation2008), we know that if the process σ t is V σ geometrically ergodic, then z t is V z geometrically ergodic for some function V z . Hence, we just need to study the ergodicity of σ t .
By simple calculations, we have
Hence, σ t can be viewed as a Markov chain of its own and studied in isolation from y t . Following the notations in Cline (Citation2007a), we can rewrite (Equation2.3) as
Obviously, B(x, e) is homogeneous in x and satisfies for some finite
, and
for some finite
. Hence, (Equation2.3) belongs to the framework of (1.2) in Cline (2007a) and we can apply Cline's (2007a) approach to study the ergodicity of σ
t
. Define a related Markov process as
To study the geometric ergodicity of σ t , we further define the Lyapounov exponent as
Then we have the following theorem.
Theorem 2.1
For the considered Θ, suppose Assumption 1 in the Appendix holds, then {σ
t
} generated from (Equation2.3) and from (Equation2.5) are φ-irreducible and aperiodic T chains on (0, + ∞). Furthermore,
is equivalently evaluated by γ and geometric ergodicity of {σ
t
} is implied by a negative value of γ, namely E{log [α(δ +e
t
)2 + β]} <0.
Proof
In terms of Cline (Citation2007a), and Cline and Pu (Citation1999), when {σ
t
} is φ-irreducible and aperiodic, geometric ergodicity of {σ
t
} is implied by a negative value of . As mentioned before, (Equation2.3) is a special case of the recursion model (1.2) in Cline (Citation2007a). If we can show the listed conditions A.1–A.4 in Cline (Citation2007a) are satisfied for (Equation2.3), then we know
is equivalent to γ. As a result, to prove Theorem 2.1, we just need to verify the mentioned conditions for (Equation2.3). Referring to Sec. 5 in Cline (Citation2007a), under Assumption 1 in the Appendix, we can see the conditions A.1, A.2, and A.4 in Cline (Citation2007a) are trivially satisfied for the case of (Equation2.3). Next, we are to show {σ
t
} and
are φ-irreducible and aperiodic T chains on (0, + ∞), which implies A.3 in Cline (Citation2007a) holds. We just consider the case of
and the conclusions for {σ
t
} can be acquired analogously.
Recall and
We have
. Suppose the continuous density function for e
t
is f(e) and we define the control set
Under Assumption 1 in the Appendix, we know O
e
= R. Let {u
t
} ⊂ O
e
be a deterministic control sequence corresponded to {e
t
}. Put u
t
= − δ +c for t = 1,…, k, where c is a small positive constant such that α
U
c
2 + β
U
< 1 and k satisfies that (note αc
2 + β <1) for some initial positive value σ0. Then we have
, which is nonzero for any positive initial value σ0. Applying Proposition 7.1.2 in Meyn and Tweedie (Citation1993), we know that
is a T-chain.
Define the control sequence as and we know
. Set
then we can get
. For t ≥ k + 2, put
and then we can get
for t ≥ k + 2, which means σ
c
= 1 is a globally attracting state for
. In terms of Proposition 7.2.5 and Theorem 7.2.6 in Meyn and Tweedie (Citation1993), we know
is ψ-irreducible. The above convergence property also shows that any circle must contain the state {σ
c
}. From Proposition 7.3.4 in Meyn and Tweedie (Citation1993), aperiodicity follows.
Remark 2.1
In practice, as in Cline (Citation2007b), we can evaluate γ by simulation approach after the parameters are estimated or find the ergodic range for a certain parameter when others are fixed. When α(δ2 + 1) + β <1, by Jensen's inequality, we immediately have γ <0.
2.2. Quasi Maximum Likelihood Estimation
Recall θ = (δ, ω, α, β)τ and θ ∈ Θ, which is a bounded parameter space for model (Equation1.2)–(Equation1.3). Suppose that the true parameter θ0 = (δ0, ω0, α0, β0)τ is an interior point of the considered parameter space Θ. We need to estimate θ based on the observations and initial values y
0, y
−1, y
−2,…. Following the convention in the literature, we consider the quasi conditional log-likelihood function (apart from a constant term)
Theorem 2.2
For model (Equation1.2)–(Equation1.3) and the considered quasi log-likelihood function L
T
(θ) given by (Equation2.8), suppose Assumptions 1–2 in the Appendix hold. Then there exists a fixed open neighborhood U(θ0) ⊂ Θ such that with probability one, as T → ∞, L
T
(θ) has an unique minimum point in U. Furthermore,
where
Remark 2.2
The proof of Theorem 2.2 is based on verifying the conditions of Lemma A.1 in Jensen and Rahbek (Citation2004), which are analogous to the ones listed in A3 of Christensen et al. (Citation2012). It can be shown that is not required to guarantee the validity of the theorem and such a result is consistent with Ling (Citation2007). In practice, initial value h
0 is needed to calculate L
T
(θ), h
t
, H
t
and the matrices Ω
I
, Ω
S
can be approximated by the relevant sample means after the parameters have been estimated.
3. Simulations and Empirical Studies
3.1. Simulations
This section examines the performance of the (Q)MLE through the Monte Carlo experiments. We study the medians and standard deviations (SD) of the estimates. The series y t is generated through model (1.2–1.3). Noting θ = (δ, ω, α, β)τ, the following five cases are considered:
Here, e t ∼ i.i.d. t(k) means e t is the innovation series that follows the distribution t(k) independently. The sample sizes are T = 300, 600, 900, respectively, and 1,000 replications are conducted. To run the estimation, we set the initial value for the conditional variance h 0 = var(y t ), θ = (δ, ω, α, β)τ ∈ [−10, 10] × [0.0001, 10] × [0.0001, 0.99] × [0.0001, 0.99].
Table 1 Medians and SDs of (Q)MLEs for model (1.2)–(1.3)
The results are summarized in Table , from which, we know the medians are close to the true values and the standard deviations are relatively small in most cases. Moreover, larger sample sizes witness a convergence trend (smaller SDs) for each case. The simulation results indicate the (Q)MLE performs well in the finite samples.
3.2. Empirical Studies
In this section, model (Equation1.2)–(Equation1.3) is applied to study some real data sets. We analyze the excess return data on the CRSP value weighted index, which includes the NYSE, the AMEX and NASDAQ. Such data can be regarded as a reasonable proxy for the stock market and it was also studied by Conrad and Mammen (Citation2008) in a different way. The riskless rate used to compute the excess returns is one-month Treasury bill rate (from Ibbotson Associates).
First, we study the monthly data whose range is from July 1926 to February 2009 (totally 992 observations). Take to be the considered excess return series and then we use (Equation1.2)–(Equation1.3) to fit the data. By minimizing (Equation2.8), we can get the estimates
The values in parentheses are the corresponding standard deviations calculated based on Theorem 2.2. Simple calculation gives α(δ2 + 1) + β = 0.9851 <1 for (Equation3.1). As mentioned in Remark 2.1, this implies the estimates satisfy the geometric ergodicity conditions. The Ljung-Box statistics of the standardized residuals give Q(3) = 5.8743(0.118), Q(12) = 17.406(0.135), where the values in the parentheses are the related p-values. The Ljung-Box statistics for the squared standardized residuals show Q(3) = 1.4144(0.702), Q(12) = 6.5556(0.886). For comparison, we also fit the data by the traditional GARCH-M model:
For (Equation3.2), the Ljung-Box statistics of the standardized residuals give Q(3) = 5.4967(0.139), Q(12) = 17.829(0.121). The Ljung-Box statistics for the squared standardized residuals show Q(3) = 1.9389(0.585), Q(12) = 6.2185(0.905). From the computed values of the Ljung-Box statistics, we can see that both (Equation3.1) and (Equation3.2) are adequate at the 5% level.Footnote 1
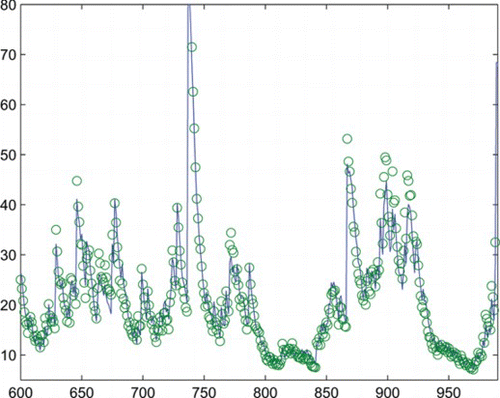
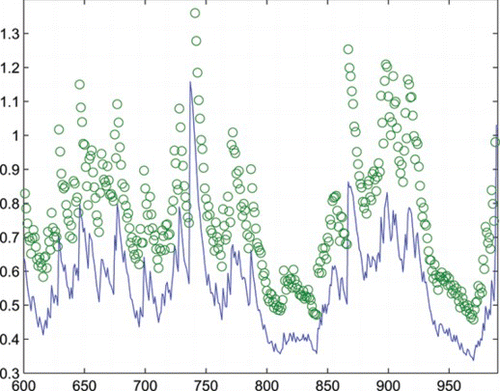
For (Equation3.1), we compute the RMSE (root mean squared error) and the MAE (mean absolute error) for the in-sample forecasts as 5.4539, 3.8223 and the corresponding ones of (Equation3.2) are 5.4669, 3.8185. Denote as the conditional variances calculated from (Equation3.1) and (Equation3.2), respectively. Correspondingly, we denote
as the in-sample forecast values. To give clear comparison, we plot
(real line) and
(circle) in Fig. ,
(real line) and
(circle) in Fig. . From the RMSEs, MAEs, and plots in the figures, we can see that both conditional variances and forecasts generated form (Equation3.1) and (Equation3.2) are quite similar, although
are generally a bit smaller than
. The above results mean that (Equation3.1) has comparable fitting effect to that of (Equation3.2) for the considered data, which can be insightful because a different GARCH process is applied.
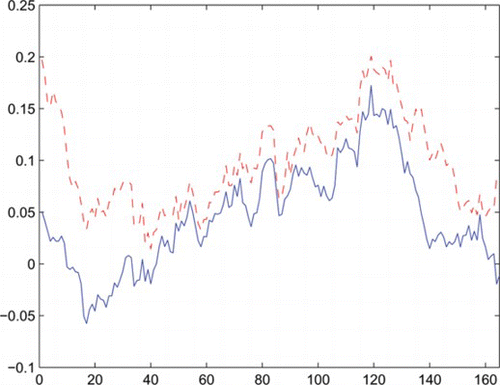
Next, based on (Equation1.2)–(Equation1.3) and the traditional model, we apply rolling-sample estimation to the weekly data whose range is from May 5, 1963 to February 27, 2009 (totally 2383 observations). Similar to Chou et al. (Citation1992), we choose the weekly data rather than the daily data to avoid the documented anomalies of day-of-the-week effects. Since April 30, 1971, for each quarter, we estimate a value for δ or the “Market Price of the Risk” in Merton (Citation1980) based on both (Equation1.2)–(Equation1.3) and the traditional model. The previous 400 observations are used to estimate the parameters and totally 165 estimators are acquired. For each estimation we record the corresponding in-sample forecast RMSEs and MAEs. Let be the estimated δ values from (Equation1.2)–(Equation1.3) and the traditional model, respectively. Accordingly, denote
as the respective RMSE and MAE sequences. For comparison, we list the percentiles of the differences between the error sequences in Table and plot
(real line),
(dashed line) in Fig. .
Table 2 Percentiles of differences between error sequences
Based on Table , it is found that the differences between the error sequences recorded from the two models are negligible. In terms of Fig. , we can see the trajectory of is analogous to that of
though the latter one is a bit higher. Consequently, similar to the results acquired from the monthly data, model (Equation1.2)–(Equation1.3) has comparable fitting performance to that of the traditional one for the considered data.
4. Conclusions
In this article, we studied a special case of the GARCH-in-Mean model in Christensen et al. (Citation2012). Ergodicity conditions are discussed and by checking the listed conditions in Lemma A.1 of Jensen and Rahbek (Citation2004), we can show the QMLE for the considered model is asymptotically normal. Through the simulations and empirical studies, it is found that the estimation performs well and the model has comparable performance in data modeling as compared to the traditional one. Our results suggest that the model of Christensen et al. (Citation2012) can be useful because it provides an alternative way to study the GARCH-in-Mean effect.
Acknowledgments
The authors are grateful to the referees for their useful comments, which led to improvements in the presentation of the article. The first two and the fourth authors were supported by research grants from the Research Committee of The Hong Kong Polytechnic University. The third author's work was partially supported by National Natural Science Foundation of China (Grant No. 10971042).
Notes
Notes. (1) Number of replications =1, 000; (2) as indicated in Sec. 3.1, different error distributions are used.
The objective of the empirical studies is to compare the performance between the considered model and the traditional one, while it should be noted that Christensen et al. (Citation2012) has shown semiparametric GARCH-in-Mean models may be more practical when analyzing the real data.
References
- Billingsley , P. ( 1995 ). Probability and Measure. , 3rd ed. New York : Wiley .
- Chou , R. , Engle , R. F. , Kane , A. ( 1992 ). Measuring risk aversion from excess returns on a stock index . J. Econometrics 52 : 201 – 224 .
- Christensen , B. J. , Dahl , C. M. , Iglesias , E. M. ( 2012 ). Semiparametric inference in a GARCH-in-Mean model . J. Econometrics 167 : 458 – 472 .
- Cline , D. B. H. ( 2007a ). Stability of nonlinear stochastic recursions with application to nonlinear AR-GARCH models . Adv. Appl. Probab. 39 : 462 – 491 .
- Cline , D. B. H. (2007b). Evaluating the Lyapounov exponent and existence of moments for threshold AR-ARCH models. J. Time Ser. Anal. 28:241–260.
- Cline , D. B. H. , Pu , H. H. ( 1999 ). Geometric ergodicity of nonlinear time series . Statistica Sinica 9 : 1103 – 1118 .
- Conrad , C. , Mammen , E. ( 2008 ). Nonparametric regression on latent covariates with an application to semi-parametric GARCH-in-mean models. Working paper, University of Mannheim .
- Engle , R. F. , Lilien , D. M. , Robins , R. P. ( 1987 ). Estimating time varying risk premia in the term structure: the ARCH-M model . Econometrica 55 : 391 – 407 .
- Jensen , S. T. , Rahbek , A. ( 2004 ). Asymptotic inference for non-stationary GARCH . Econometric Theor. 20 : 1203 – 1226 .
- Ling , S. ( 2004 ). Estimation and testing of stationarity for double autoregressive models . J. Roy. Statist. Soc. B 66 : 63 – 78 .
- Ling , S. ( 2007 ). A double AR (p) model: structure and estimation . Statistica Sinica 17 : 161 – 175 .
- Meitz , M. , Saikkonen , P. ( 2008 ). Ergodicity, mixing, and existence of moments of a class of markov models with applications to GARCH and ACD models . Econometric Theor. 24 : 1291 – 1320 .
- Merton , R. ( 1980 ). On estimating the expected return on the market: an exploratory investigation . J. Finan. Econ. 8 : 323 – 361 .
- Meyn , S. P. , Tweedie , R. L. ( 1993 ). Markov Chains and Stochastic Stability . London : Springer-Verlag .
Appendix
We make the following assumptions for model (Equation1.2)–(Equation1.3).
Assumption 1
The i.i.d (0, 1) process {e
t
} satisfies , and has a continuous symmetric probability density function which is positive everywhere.
Assumption 2
The series {y t , h t } generated from model (Equation1.2)–(Equation1.3) are strictly stationary and geometrically ergodic for the considered parameter space Θ.
Lemma A.1 (Lemma 1 of Jensen and Rahbek, Citation2004)
Denote L T (ψ) as a function of the observations y 1,…, y T and the parameter ψ ∈ Ψ ⊆ R k . Suppose ψ0 is an interior point of Ψ. Assume L T (.): R k → R is three times continuously differentiable in ψ and that:
(A1) as | |||||
(A2) as | |||||
(A3) max i, j, k=1,…, p+2sup ψ∈N(ψ0)|∂3 L T (ψ)/∂ψ i ∂ψ j ∂ψ k | ≤c T . | |||||
Here, N(ψ0) is a neighborhood of ψ0 and . Then there exists a fixed open neighborhood U(ψ0) ⊆ N(ψ0) such that:
(B1) as T → ∞, with probability one that there exists a minimum point | |||||
(B2) As | |||||
Before giving proof for Theorem 2.2, we need to state some expressions and several lemmas. Let symbol variables s 1, s 2, s 3 take values from symbol set {i, j, k}. In terms of (Equation2.8), it is not difficult to get the derivatives of the quasi likelihood function with respect to θ:
Note that ; then we have
Simple recursion gives
Define
Lemma A.2
Let h
t
(θ), h
t
(β) be given as in (Equation5.9) and (Equation5.11). Note that h
t
(θ0) = h
t
(β0) = h
t
, then we have and for any t, s
Proof
Note that
Similarly, we can get , which together with (Equation5.12) implies the last two inequalities hold.
Lemma A.3
Define the processes
Proof
The above results can be gotten by using similar argument to that of Lemma 3 in Jensen and Rahbek (Citation2004).
By (Equation5.10), it is not difficult to get
Lemma A.4
With 0 < β L ≤ β, β0 ≤ β U < 1,
Proof
When β0 ≤ β, we know In terms of (Equation5.11), we have
When β ≤ β0, we know Similar to (Equation5.22), we have
Further, in terms of Lemma A.2 and (Equation5.24), we have
When β ≤ β0, the inequality holds by (Equation5.24). Next, for β0 ≤ β, Lemma A.2 gives
The second equality can be explained by (Equation5.21). Provided β0 ≤ β, (Equation5.22) gives
Proof of Theorem 2.2
According to Lemma A.1, we just need to show the conditions A1–A3 hold. We consider condition A1 first. Recall . From (Equation5.1)–(Equation5.2), we know
Consider any non zero vector c = (c 1, c 2, c 3, c 4)τ, then we have
Let ℱ
t−1: = σ(e
t−1,…, e
1, y
0, y
−1,…) be the information set up to time t − 1, then we know {W
t
} is a martingale difference with respect to ℱ
t−1 and . Under Assumptions 1–2, it is not difficult to get
Consequently, we have
Furthermore, given any δ > 0, we have
The above limit can be explained by the fact: . By the martingale central limit theorem, see, for example, Theorem 35.12 in Billingsley (Citation1995) we deduce that
, which means
Applying the double expectation formula we can get
For condition A3 of Lemma A.1, we just show sup θ∈Θ|∂3 L T (θ)/∂β3| is controlled by a positive ergodic sequence that has desired moments. Other cases can be easily proved by noting the fact: ∂ i h t (θ)/∂δ i = 0, ∂ j h t (θ)/∂ω j = ∂ j h t (θ)/∂α j = 0 for i = 1, 2, 3, j = 2, 3, and
Then according to (Equation5.3)–(Equation5.5), it can be calculated that
We also have
Based on Lemma A.2 and Lemma A.4, it can be seen that
Note , in terms of Lemma A.2 and (Equation5.30)–(Equation5.33), then there exists a constant K such that
From Lemma A.3, Lemma A.4, and (Equation5.35), we know w t (β) in (Equation5.36) is bounded by some ergodic w t that has desired moments. Hence, we have shown A3 in Lemma A.1 holds for the case of ∂3 L t (θ)/∂β3. Other situations can be proved by similar argument, which ends the proof of Theorem 2.2.