Abstract
A balanced incomplete block design (BIBD) is instrumental in design of experiments. This is usually constructed by algebraic methods such as finite algebra or difference sets. However, in algebraic approaches, no unified method exists, and each BIBD has been constructed in some ad hoc ways. On the other hand, computer-based methods apply the same algorithm to all BIBDs; hence, these are unified approaches. Although various meta-heuristic algorithms have been tried, the success of these methods has been rather limited. This article presents an alternative approach to this problem that formulates the problem as a nonlinear mixed integer programming problem. We develop a branch-and-bound algorithm to solve this, and a tabu search algorithm to overcome some weakness in the former algorithm. We compare the performance of these algorithms against some previously developed algorithms, and demonstrate that our algorithms are competitive to these methods.
1. Introduction
Let V be a set of v elements called points and B be a collection (i.e. multi-set) of b non-empty subsets of V called blocks. (V, B) is a balanced incomplete block design (BIBD Citation3 Citation8 Citation12 Citation22), if the following conditions are satisfied.
-
(i) Each point is contained in exactly r blocks.
-
(ii) Each block contains exactly k points.
-
(iii) Every pair of distinct points is contained in exactly λ blocks.
With positive integer parameters , this is denoted as BIBD
. BIBD has its origin in statistical design of experiments Citation6, and recently it is also applied to the coding theory Citation2
Citation7, failure diagnosis and group testing Citation10, and scheduling sports leagues Citation1 among others.
In matrix notation, BIBD is a v×b binary matrix X=(x il ) such that
From these relations, the following is easily shown Citation12.
Proposition 1.1
In BIBD
parameters satisfy
Then, b and r are determined by as
Theorem 1.2
Let v and λ be positive integers, and k=3 or k=4. Then, BIBD
exists if and only if b and r determined by Equations (7) and (8) are both integers.
Triple system is the special case of BIBD with k=3, and Steiner triple system is with k=3 and λ=1 Citation8. These are denoted as TS(v, λ) and STS(v), respectively. For the Steiner triple system, the above result was shown by Kirkman Citation16 as early as in 1847, together with a construction method for STS(v). Hanani Citation14 proved similar results for k=5 and k=6 with some minor exceptions. However, except for these, neither necessary and sufficient conditions nor the construction method of BIBDs is known in general.
Various approaches have been tried for the construction of BIBDs. Among these, algebraic methods, such as finite projective (or affine) geometry and difference sets
Citation12
Citation22, have been the main stream and most successful, with most of the BIBDs known today being discovered by these methods. Extensive list of BIBDs, as well as unknown BIBDs up to date, are available in the handbook by Colbourn and Dinitz Citation8. Unfortunately, these methods are quite complicated, and no unified approach exists for the construction of BIBDs by these methods. Thus, BIBDs have been constructed for each set of parameters by some ad hoc methods, in a case-by-case way.
Computational methods, such as constraint programming Citation20, neural networks Citation18 and meta-heuristic algorithms Citation5 Citation17, provide a unified framework. However, the ability of these methods for the construction of BIBDs has been rather limited, until recently some success stories have been reported. For example, by an exhaustive computer search over more than 90,000 days in total, Bilous et al. Citation4 proved that no (22,8,4)-BIBD exists. Similarly, Houghten et al. Citation15 declared the non-existence of (46, 6, 1)-BIBD. On the other hand, Morales Citation19 discovered six new BIBDs by an elaborate tabu search Citation11. In spite of these few successes, heuristic algorithms are usually quite time-consuming.
In this article, we present an alternative approach for the construction of BIBDs that formulates the problem as a nonlinear mixed integer programming (MIP) problem. If this problem is solved to optimality, we either obtain a BIBD, or have the evidence that no BIBDs exist for the given set of parameters. In this sense, our approach is complete, as opposed to other heuristic methods where success of the algorithms is totally by chance.
The organization of this paper is as follows. In Section 2, after formulating the problem as a nonlinear MIP problem, we present a backtracking framework to solve this nonlinear optimization problem by solving a series of linear MIP problems. Based on this, in Section 3, we develop a branch-and-bound algorithm for this problem. We find that this method is successful for triple systems, but for some BIBDs, it takes very long computing time, or even unable to produce a solution. To overcome this weakness, we present a tabu search algorithm in Sections 4, and 5 to compare these algorithms against the local search method proposed by Prestwich Citation21 on the 86 benchmark instances given in his paper. From these 86 instances, we were able to solve 78 instances, while the local search algorithm of Prestwich Citation21 solved only 63 instances.
2. Backtracking algorithm
Finding a matrix satisfying EquationEquations (1)–Equation(4)
is a kind of constraint satisfaction problem which can be transformed into the following nonlinear 0–1 programming problem Citation23.
Note that equalities (1)–(3) are relaxed to inequalities (10)–(12), and the objective function is simply the sum of the left-hand sides of these inequalities. Then, the following is trivial.
Theorem
-
(i) P is always feasible.
-
(ii) For an arbitrary feasible solution X=(x ij ) to P, let z(X) denote its objective value. Then, we have
-
(iii) If Equation (14) is satisfied with equality, Equations (10)–(12) are also satisfied with equality, and thus X gives a BIBD
Therefore, if equality holds in EquationEquation (14) with respect to an optimal solution X* to P, we are done. Otherwise, if
, no BIBD exists. However, since P is a nonlinear 0–1 programming problem, it is difficult to get an optimal solution. Thus, we propose an incremental approach that determines rows of X one by one.
Now, suppose that the first j rows of X is known as . From EquationEquations (1)
–Equation(4)
, this is a binary matrix that satisfies the followings.
If such an is found, we can augment X
j
to a
matrix
To obtain a binary vector satisfying EquationEquations (18)
–Equation(20)
, we formulate the following optimization problem.
Contrary to nonlinear P, P
j
(X
j
) is a linear 0–1 programming problem which can be solved (in many cases) using free or commercial MIP solvers. Let the optimal objective value to P
j
(X
j
) be . Then, since the objective function Equation(22)
is the sum of the left-hand sides of EquationEquations (23)
and Equation(25)
, any optimal solution to P
j
(X
j
) gives a binary
satisfying EquationEquations (18)
–Equation(20)
if and only if
Without loss of generality, the first and second rows of X j can be assumed to be
Example 2.2 For BIBD (12,22,11,6,5), except for trivial inequalities and 0–1 conditions, P 2(X 2) is
Here, we note that the optimal solution to P
j
(X
j
) may not be unique even if EquationEquation (27) is satisfied. If this is the case, we do not know exactly which optimal solution to adopt in EquationEquation (21)
. In the branch-and-bound algorithm to be developed in the next section, we list up all the optimal solutions of P
j
(X
j
) and define its children by appending each of these solution vectors to X
j
. Thus, we have a tree of subproblems rooted at P
2(X
2), and traversing all the subproblems obtain a BIBD, or prove that no BIBD exists.
To list up all the optimal solutions of P j (X j ), we introduce the following auxiliary problem.
Example 2.3 Applying the above algorithm to P
7(X
7) with , we obtain
, which is the eighth row of X
8 in EquationEquation (30)
. From the indexes of non-zero elements of
, we have
. Then, auxiliary problems are generated by adding constraints
and
to P
7(X
7) as
{u
s
}), and the feasible region of
is divided into mutually disjoint feasible regions of
. Here for s=0, we mean
, and from EquationEquation (23)
is the unique optimal solution to this problem. Then, by solving
recursively, we obtain all the optimal solutions to
, together with
.
3. A branch-and-bound method
We construct a branch-and-bound algorithm Citation23
Citation24 to find a BIBD in the following way. First of all, we define as the continuous relaxation of
, and
denotes an optimal solution to this problem with the corresponding objective value
. Then, we can terminate subproblem
if
Algorithm
BAB_BIBD
Input: j, X j , F, R.
-
Step 1. If j=v, X j is a BIBD. Output this and stop.
-
Step 2.
-
(i) Solve an LP problem
and obtain
and
-
(a) If
then terminate this subproblem and return.
-
(b) Otherwise, if the solution
is a 0–1 vector, let
, and go to Step 3.
-
-
Solve an IP problem
and obtain
and
If
terminate this subproblem and return.
-
-
Step 3. Append
to X j and update this to X j+1 through EquationEquation (21)
. Call BAB_BIBD
recursively.
-
Step 4. Let
be the set of indexes such that
and
For
do
-
(i) Let
and
-
(ii) Call BAB_BIBD
recursively.
-
-
Step 5. No BIBDs exist. Stop.
Some remarks are in order on the branch-and-bound strategies. First of all, linear relaxation is not mandatory, i.e. we may skip part (i) of Step 2. In the standard case, we solve an LP problem first, and then solve P
j
(X, F, R) if necessary, as described in the algorithm. This is referred to as the bounding strategy LP. If we skip part (i) in Step 2 and go directly to part (ii), we call this bounding strategy IP.
Next, recursive calls to subproblems can be carried out in the reverse order. For the problem in Example 2.3, the original algorithm calls subproblems in the order of
. We call this the forward branching strategy (FWD). In the backward strategy (BWD), these subproblems are called reversely as
. We denote these strategies explicitly as BAB_BIBD (bounding strategy, branching strategy), such as BAB_BIBD(LP, FWD).
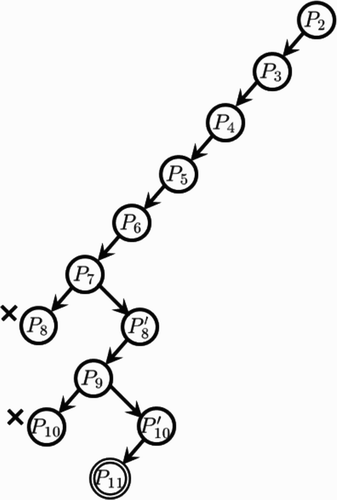
Example 3.1 shows the behaviour of the algorithm under the bounding strategy IP and branching strategy FWD, i.e. BAB_BIBD(IP, FWD). As in Example 2.2, subproblem P
8 is terminated, and by solving we obtain an alternative solution
that replaces the eighth row of X
8 in Example 2.2. In , this is P′8. Restarting from this point, the process stops again at P
10. Here, we switch to P′10, and finally obtain a BIBD as
Example 3.2
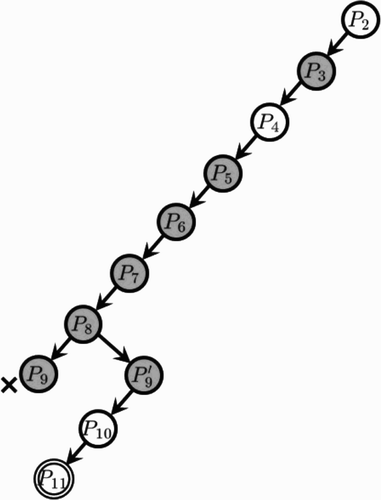
If we take bounding strategy LP instead of IP in the previous example, the algorithm BAB_BIBD(LP, FWD) produces the tree of subproblems as depicted in . Here, shadowed nodes show the subproblems where both of LP and IP problems are solved, while at the remaining nodes we solve only LP problems. Thus, we obtain a BIBD
Example 3.3
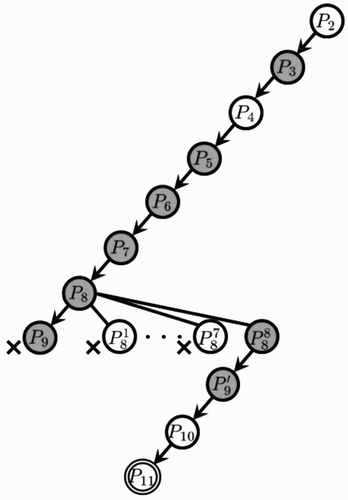
shows the behaviour of the backward branching strategy, i.e. BAB_BIBD(LP, BWD). The algorithm proceeds exactly the same way as in the previous example until again P
9 is terminated (compare and ). Then, auxiliary subproblems are generated and examined as in the previous example but in the reverse order. The first seven subproblems are terminated due to EquationEquation (33)
, we restart from
and at P
11 obtain a BIBD
Now, we evaluate the performance of the branch-and-bound algorithm for triple systems TS(v, λ). shows the result of BAB_BIBD(LP, FWD) on a DELL Precision 670 computer (CPU: Xeon ) with CPLEX 10.100 Citation9 to solve LP and IP problems. Here shown are the number of subproblems generated (#Subp), the number of LP and IP problems solved (#LP, #IP) and the CPU time in seconds. We solved three randomly selected instances for each value of
, within v≤200 and b≤3000.
Table 1. Result of BAB_BIBD(LP, FWD) for triple systems TS(v, λ).
From this table, we see that in almost all instances , which means that backtracking seldom occurs in triple systems. Next, #IP is relatively small, i.e. in most cases we obtain BIBD by solving approximately v LP and some additional IP problems. This implies that we frequently obtain 0–1 solutions by solving only LP problems, and thus the bounding strategy LP is well suited to this case. Thus, the branch-and-bound method works effectively for triple systems.
BAB_BIBD is often inefficient for problems where backtracking occurs frequently. For example, in solving BIBD(10,15,6,4,2) by BAB_BIBD(LP, FWD), we had to solve 1,207,105 LP and 343,523 IP problems and the CPU time was 2068 s. We were unable to solve BIBD(16,16,6,6,2) within 3600 s, while the local search algorithm by Prestwich Citation21 solved this within 1 s on a slower computer.
The reason for this difficulty of BAB_BIBD for some BIBDs may be explained as follows. In the case of triple systems, usually there are many different (non-isomorphic) solutions for each set of parameters Citation8, and thus it does not much matter which optimal solution of P
j
(X
j
) we choose in augmenting X
j
to X
j+1 through EquationEquation (21). In most cases, any solution is satisfactory, and no backtracking is necessary. On the other hand, in general BIBDs, there are only a few number of solutions for each set of parameters. In such a case, we must be very careful in selecting a solution of P
j
(X
j
). If we make a wrong choice and ‘bad’ rows are included in X
j
, it takes a long time until we backtrack and eliminate these bad rows.
4. Tabu search
To overcome the weakness of BAB_BIBD to some instances, we propose a tabu search method. The idea is that in X
j
we may have some bad rows, which means a 0–1 vector that is not included in any BIBDs of the given set of parameters. Then, after solving P
j
(X
j
), we make a guess whether bad rows are included in X
j
. If we find a doubtful row, we eliminate it and restart with the reduced X
j−1. More specifically, if we solve P
j
(X
j
) and obtain an optimal solution with
, we move forward by adding
to X
j
as we did in the BAB_BIBD. On the other hand, if
we have either
To prevent a removed vector from returning to X
j
in the subsequent few steps, we introduce a tabu list 𝒯 to keep the eliminated vectors ‘frozen’ for a certain period of steps. The size of 𝒯 is specified by a parameter TL (tabu length), and vectors in the tabu list are forbidden to be an optimal solution to P
j
(X
j
). To realize this, let be the current tabu list, and consider the following 0–1 programming problem.
Algorithm 1
TABU_BIBD
-
Step 1. Let j:=2, X 2 be given as Equation (28), and
-
Step 2. If j=v, then X j is a BIBD. Output this and stop.
-
Step 3. Solve an IP problem
If
, go to Step 4. Otherwise go to Step 5.
-
Step 4. Append the solution to X j and augment it to X j+1. Go back to Step 2 with
-
Step 5. If there exists a row i satisfying Equation (37), go to Step 6. Otherwise pick up a row vector from X j at random and go to Step 6.
-
Step 6. Eliminate the selected vector from X j , let
and add the eliminated vector to the tabu list 𝒯. (If
the oldest vector is removed from 𝒯.)
-
Step 7. If terminating condition is satisfied, then print ‘Tabu search failed’, and stop. Otherwise go back to Step 2.
Example 4.1 In applying the tabu search algorithm to BIBD(16,16,6,6,2) where BAB_BIBD failed to find a solution within 3600 CPU seconds, the tabu search produced a correct BIBD in 0.02 s as follows. Initially, the tabu list is initialized as . The algorithm behaves exactly the same way as BAB_BIBD(IP, FWD) until at j=8 we obtain
Prestwich Citation21 proposed a local search algorithm, and tried 86 instances with v and b satisfying vb≤1000. compare his result against our branch-and-bound and tabu search methods with MIP solvers. In these tables, CPU time in seconds is shown for each method. The column of ‘Prestwich’ is the result of his method on a DEC Alphaserver 100A 5/300 computer (300 MHz), while ‘BAB’ is by the branch-and-bound algorithm BAB_BIBD(LP, FWD), and ‘TABU’ is by TABU_BIBDEquation(10) on a faster DELL Precision 670 machine
. Computation was truncated (and shown in tables by –) at 2 million backtracks in ‘Prestwich’ and 3600 CPU seconds in our algorithms.
Table 2. Result of computation for Prestwich's 86 instances (Part 1).
Table 3. Result of computation for Prestwich's 86 instances (Part 2).
Table 4. Result of computation for Prestwich's 86 instances (Part 3).
From these tables, we see that the branch-and-bound method solves more instances than the Prestwich method. However, in some instances, it took much longer time, or even unable to solve, while the same instances were solved easily by the Prestwich local search algorithm. By the tabu search method of this paper, we were able to solve all the instances that were solved by Prestwich. The tabu search algorithm solved some additional instances that neither Prestwich's nor the branch-and-bound algorithms were able to solve.
gives a summary of the numbers of instances out of 86 solved by Prestwich's and our methods. The branch-and-bound method solved approximately 10 more instances than Prestwich's, irrespective of the bounding and branching strategies. Tabu search was able to solve 10 additional instances, irrespective of the tabu length.
Table 5. Summary of computation.
5. Conclusion
We have formulated the problem of constructing BIBDs as a nonlinear MIP problem, and presented branch-and-bound and tabu search algorithms that makes use of MIP solvers. The developed branch-and-bound method was successful for triple systems, but it sometimes encountered difficulty for general BIBDs. Tabu search improved this situation to some extent. In some instances, it succeeded in eliminating bad rows in earlier stages, and obtained BIBDs that the branch-and-bound method could not. Compared with heuristic algorithms proposed by previous researchers, our algorithms appear to be competitive. However, even with these algorithms we were unable to find new BIBDs. To solve problems with v≥30, some new bounding conditions are required, and thus make the algorithm more efficient.
Acknowledgements
The authors are grateful to two anonymous referees for their constructive criticisms and suggestions, which improved the exposition of the paper significantly.
References
- Anderson , I. 2006 . Combinatorial Designs and Tournaments , New York : Oxford University Press .
- Beth , T. , Jungnickel , D. and Lenz , H. 1999 . Design Theory , 2 , Cambridge : Cambridge University Press .
- Biggs , N. L. , Lloyd , E. K. and Wilson , R. J. 1995 . The history of combinatorics, in Handbook of Combinatorics , Edited by: Graham , R. L. , Grötschel , M. and Lovász , L. Vol. II , 2163 – 2198 . Amsterdam : Elsevier .
- Bilous , R. , Lam , C. W.H. , Thiel , L. H. , Li , B. P.C. , van Rees , G. H.J. , Radziszowski , S. P. , Holzmann , W. H. and Kharaghani , H. 2006 . There is no 2-(22, 8, 4) block design . J. Combin. Des. , 15 : 262 – 267 .
- Bofill , P. , Guimera , R. and Torras , C. 2003 . Comparison of simulated annealing and mean field annealing as applied to the generation of block designs . Neural Netw. , 16 : 1421 – 1428 .
- Box , G. E. , Hunter , W. G. and Hunter , J. S. 2005 . Statistics for Experimenters: Design, Innovation, and Discovering , 2 , Hoboken : John Wily & Sons .
- Brouwer , E. 1995 . Block designs, in Handbook of Combinatorics , Edited by: Graham , R. , Gröetschel , M. and Lovász , L. Vol. I , 693 – 771 . Amsterdam : Elsevier .
- Colbourn , C. J. and Dinitz , J. H. 2007 . Handbook of Combinatorial Designs , 2 , New York : Chapman & Hall/CRC .
- CPLEX Ver. 11.0, ILOG, 2008. Available at http://www.ilog.com/products/cplex/
- Du , D.-Z. and Hwang , F. K. 2000 . Combinatorial Group Testing and its Applications , 2 , Singapore : World Scientific Publication .
- Glover , F. and Laguna , M. 1997 . “ Tabu Search ” . Norwell : Kluwer .
- Hall , M. Jr. 1998 . Combinatorial Theory , 2 , New York : John Wiley & Sons .
- Hanani , H. 1961 . The existence and construction of balanced incomplete block designs . Ann. Math. Stat. , 32 : 361 – 386 .
- Hanani , H. 1975 . Balanced incomplete block designs and related designs . Discrete Math. , 11 : 255 – 369 .
- Houghten , S. K. , Thiel , L. H. , Janssen , J. and Lamet , C. W.H. 2001 . There is no (46,6,1) block design . J. Combin. Des. , 9 : 60 – 71 .
- Kirkman , T. 1847 . On a problem in combinations . Cambridge Dublin Math. J. , 2 : 191 – 204 .
- Kreher , D. L. and Stinson , D. R. 1999 . Combinatorial Algorithms: Generation, Enumeration and Search , Boca Raton : CRC Press .
- Kurokawa , T. and Takefuji , Y. 1992 . Neural network parallel computing for BIBD problems . IEEE Trans. Circuits Syst. II , 39 : 243 – 247 .
- Morales , L. B. 2000 . Constructing difference families through an optimization approach: Six new BIBDs . J. Combin. Des. , 8 : 261 – 273 .
- Prestwich , S. Balanced incomplete block design as satisfiability . Irish Conference on AI and Cognitive Science . Cork. Vol. 12 , pp. 189 – 198 .
- Prestwich , S. 2002 . A local search algorithm for balanced incomplete block designs , Cork : University College Cork . Lecture Notes in Artificial Intelligence, Cork Constraint Computation Centre
- Sachkov , V. N. 1977 . Combinatorial Methods in Discrete Mathematics , Cambridge : Cambridge University Press .
- Schrijver , A. 1998 . Theory of Linear and Integer Programming , Amsterdam : John Wiley & Sons .
- Sedegewick , R. 1998 . Algorithms in C , 3 , Boston : Addison-Wesley .
- Stinson , D. R. 2004 . Combinatorial Designs: Construction and Analysis , New York : Springer-Verlag .