On total labelings of graphs with prescribed weights

Peer review under responsibility of Kalasalingam University.

Abstract

Let be a finite, simple and undirected graph. The edge-magic total or vertex-magic total labeling of is a bijection from onto the set of consecutive integers , such that all the edge weights or vertex weights are equal to a constant, respectively. When all the edge weights or vertex weights are different then the labeling is called edge-antimagic or vertex-antimagic total, respectively.

In this paper we provide some classes of graphs that are simultaneously super edge-magic total and super vertex-antimagic total, that is, graphs admitting labeling that has both properties at the same time. We show several results for fans, sun graphs, caterpillars and prisms.

Keywords:

• Super edge-magic total labeling
• Super vertex-antimagic total labeling
• Total labeling

1 Introduction

We consider finite undirected graphs without loops and multiple edges with vertex set and edge set , where , . A labeling of a graph is any mapping that maps a certain set of graph elements to a certain set of positive integers. If the domain is the vertex (or edge) set, respectively, the labeling is called vertex (or edge) labeling, respectively. If the domain is both vertices and edges then the labeling is called a total labeling. The edge weight of an edge under the total labeling is the sum of the edge label and the labels of its end vertices. The vertex weight of a vertex under the total labeling is defined as sum of the vertex label itself and the labels of its incident edges.

A labeling is called edge-magic total (vertex-magic total) if the edge weights (vertex weights) are all the same. If the edge weights (vertex weights) are pairwise distinct then the total labeling is called edge-antimagic total(vertex-antimagic total). A graph that admits edge-magic total (edge-antimagic total) labeling or vertex-magic total (vertex-antimagic total) labeling is called an edge-magic total (edge-antimagic total) graph or vertex-magic total (vertex-antimagic total) graph, respectively.

The subject of edge-magic total graph has its origin in the work of Kotzig and Rosa [1]. Vertex-magic total graphs are introduced by MacDougall, Miller, Slamin and Wallis in [2], see also [3,4]. The notation of edge-antimagic total labeling was introduced by Simanjuntak, Bertault and Miller in [5] as a natural extension of magic valuation defined by Kotzig and Rosa in [1]. The vertex-antimagic total labeling of graphs was introduced in [6], see also [7]. If moreover the vertices are labeled with the smallest possible labels then, as is customary, the labeling is referred to as super. The concept of super-magic graphs was introduced by Stewart [8]. For further information on these types of labelings, one can see [9,7,10,11].

In [12] Bača, Miller, Phanalasy, Ryan, Semaničová-Feňovčíková and Sillasen proved that there exist some classes of stars, paths and cycle graphs which are simultaneously edge-magic total and vertex-antimagic total or simultaneously vertex-magic total and edge-antimagic total.

In this paper we will prove that some classes of fans, suns, caterpillars and prism graphs are simultaneously super edge-magic total and super vertex-antimagic total. For every of these graph we describe a total labeling that has both properties at the same time.

2 Fans, sun graphs, caterpillars and prisms

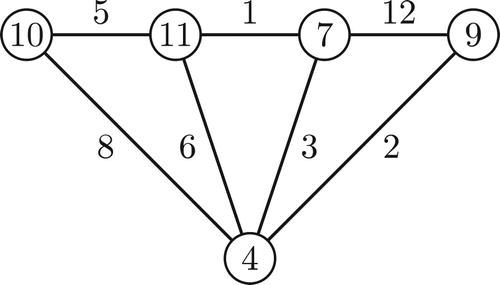
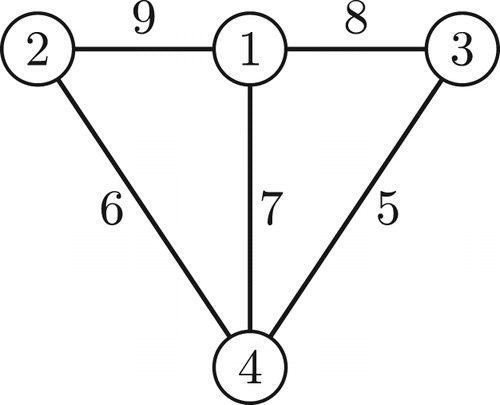
A fan , , is a graph obtained by joining all vertices of path on vertices to another vertex, called center. The fan graph contains vertices and edges.

Theorem 1

The fan is simultaneously super edge-magic total and super vertex-antimagic total if and only if .

Proof

In [13], see also [7], is proved that the fan has a super edge-magic total labeling if and only if . The fan is isomorphic to the cycle . In [12] is showed that the cycle is not simultaneously super edge-magic total and super vertex-antimagic total.

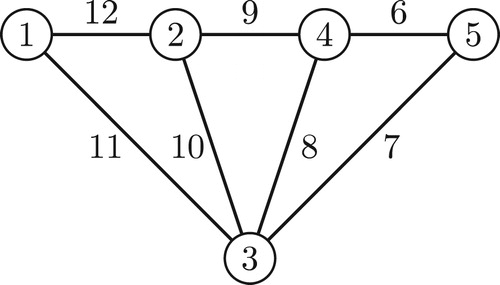
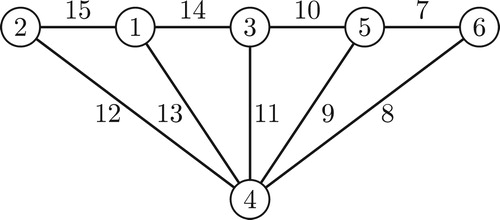
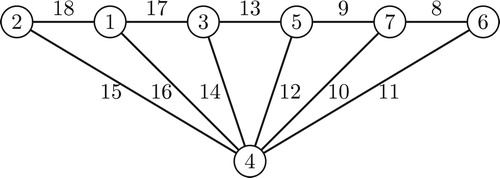
For are the required labelings depicted in Figs. 1 ^{Fig. 2Fig. 3}through 4.

Fig. 1 depicts a simultaneously super edge-magic total and super vertex-antimagic total labeling for with edge weights equal 12 and vertex weights .

A super edge-magic total labeling of the fan with edge weights 15 is illustrated in Fig. 2. This total labeling is also super vertex-antimagic with vertex weights .

Fig. 3 shows a simultaneously super edge-magic total and super vertex-antimagic total labeling of the fan with edge weights 18 and with vertex weights .

A total labeling of the fan with constant edge weights 21 is given in Fig. 4. This total labeling is also super vertex-antimagic with vertex weights .  ■

Fig. 1 A simultaneously super edge-magic total and super vertex-antimagic total labeling of the fan .

Fig. 2 A simultaneously super edge-magic total and super vertex-antimagic total labeling of the fan .

Fig. 3 A simultaneously super edge-magic total and super vertex-antimagic total labeling of the fan .

Fig. 4 A simultaneously super edge-magic total and super vertex-antimagic total labeling of the fan .

In the following lemma we prove that number of pendant edges incident with a given vertex in a simultaneously super edge-magic total and super vertex-antimagic total graph is at most 1.

Lemma 1

Let be a simultaneously super edge-magic total and super vertex-antimagic total graph. Then every vertex of can be incident with at most one pendant edge.

Proof

Let be a simultaneously super edge-magic total and super vertex-antimagic total graph and let be the corresponding labeling of . Let us assume that there is a vertex that is adjacent to more than one vertex of degree 1, say , are two of them. As is a super edge-magic total labeling then the weights of edges and are the same, i.e.,

and thus

what is a contradiction to the fact that is also vertex-antimagic.  ■

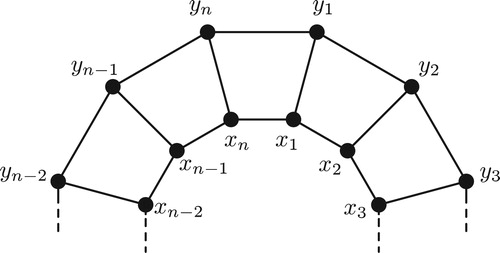
Now we will investigate graphs obtained by attaching pendant vertices to every vertex of a given graph . These graphs can be alternatively obtained as a corona product of a graph and a totally disconnected graph on vertices, denoted by . A cycle of order with pendant edges attached at each vertex, i.e., , is called an -crown with cycle of order . A 1-crown, or only a crown or a sun graph, is a cycle with exactly one pendant edge attached at each vertex of the cycle. We will use notation for this graph. We denote the elements of the sun graph such that its vertex set is and its edge set is where the indices are taken modulo . Thus the sun has vertices and edges, see Fig. 5.

Fig. 5 Sun graph .

According to Lemma 1 we immediately have the following result.

Observation 1

If the -crown with cycle of order , i.e., , is a simultaneously super edge-magic total and super vertex-antimagic total graph then .

Next we will deal with the existence of total labeling of the sun graph which has simultaneously super edge-magic properties and super vertex-antimagic properties.

Theorem 2

For every odd positive integer , , the sun graph is simultaneously super edge-magic total and super vertex-antimagic total.

Proof

Define a total labeling in the following way:

It is not difficult to see that the labeling is a total labeling and moreover the vertex labels are the smallest possible labels. For edge weights we have

Thus the total labeling is a super edge-magic labeling of the sun graph for every odd , . Let us consider the vertex weights under the total labeling .

As for (1) we have that the weights of vertices form an arithmetic progression with difference . Also the weights of vertices constitute the set of consecutive integers We can also easily see that for all . This shows that is vertex-antimagic as well. It means that for every odd , , the sun graph is simultaneously super edge-magic total and super vertex-antimagic total.  ■

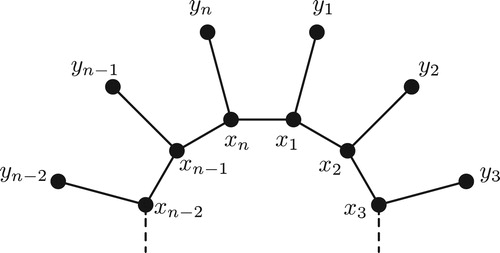
If we remove one edge on the cycle of the sun graph then the resulting graph is a tree and it is a special class of caterpillar. We denote this tree as .

Theorem 3

For every odd positive integer , , the tree is simultaneously super edge-magic total and super vertex-antimagic total.

Proof

Let us consider the tree as the sun graph with the edge deleted. By the labeling defined in the proof of Theorem 2, we define a labeling of as follows: for every .

Since the label of removed edge in under the total labeling is the largest one then the labeling is a total labeling of the tree with labels from 1 up to . It is easy to see that the total labeling preserves super edge-magic properties.

For proving that the total labeling preserves also super vertex-antimagic properties it is sufficient to show that the vertex weights of vertices and are distinct from other vertices of the tree . In fact, using (1(1) ), for we get and for Also for and for

This proves that the tree is simultaneously super edge-magic total and super vertex-antimagic total for every odd , .  ■

The prism , , is a cubic graph which can be represented as a Cartesian product of a path on two vertices with a cycle on vertices. Let be the vertex set and where the indices are taken modulo , be the edge set of the prism , see Fig. 6. The prism has vertices and edges.

Fig. 6 The prism .

Next theorem shows that there exists a total labeling of the prism which has super edge-magic and also super vertex-antimagic properties.

Theorem 4

For every odd positive integer , and the prism is simultaneously super edge-magic total and super vertex-antimagic total.

Proof

We define a total labeling as follows:

It is not difficult to check that is a bijection and the vertices of prism under the total labeling receive labels from the set . So, the total labeling is super. For edge weights under the labeling we have

Thus the labeling is a super edge-magic total labeling.

Let us consider the vertex weights under the labeling :

Since then for even, , is distinct to for odd, . Moreover, for .

By the same reason for even, , is distinct to for odd, . It is easy to see that for .

Hence is a super vertex-antimagic total labeling.

Therefore the prism is simultaneously super edge-magic total and super vertex-antimagic total for every odd , , . This concludes the proof. ■

3 Conclusion

In the paper we dealt with the problem of finding total labelings of some classes of graphs that are simultaneously super vertex-magic and super edge-antimagic. We showed the existence of such labelings for certain classes of graphs, namely fans, sun graphs, one class of caterpillars and prisms. In [12] authors ask not only for finding classes of graphs that are simultaneously vertex-magic and edge-antimagic but also graphs that are simultaneously vertex-antimagic and edge-magic.

For the fan we proved that it is simultaneously super edge-magic total and super vertex-antimagic total if and only if . In [14] it is proved that the fan is vertex-magic total if and only if . Note that for and the described labelings induce also distinct edge weights. In Fig. 7 we present a simultaneously vertex-magic total and edge-antimagic total labeling of the fan .

Fig. 7 A simultaneously vertex-magic total and edge-antimagic total labeling of the fan .

Moreover, in [15], it is showed that the fan is super vertex-magic total if and only if . However, in this case the considered edge weights are also the same, which means that no fan is simultaneously super vertex-magic total and super edge-antimagic total. So we pose the following open problem.

Open Problem 1

For the fan , , determine if there is a simultaneously vertex-magic total and edge-antimagic total labeling.

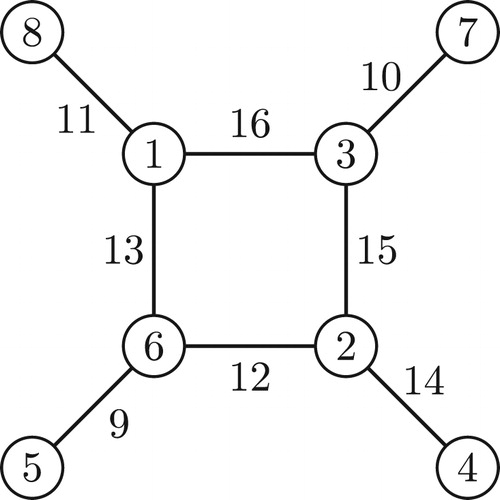
For sun graph we proved that for every odd, , the sun graph is simultaneously super edge-magic total and super vertex-antimagic total. Another interesting question is to settle the existence question for even orders. We found a simultaneously super edge-magic total and super vertex-antimagic total labeling for sun graph , see Fig. 8. Although we were unable to find such labelings for bigger even numbers, we still believe that a computer aided search would help to find them.

Fig. 8 A simultaneously super edge-magic total and super vertex-antimagic total labeling of the sun graph .

Open Problem 2

For the sun graph , even, , determine if there exists a total labeling which is simultaneously super edge-magic and super vertex-antimagic.

It is a simple observation that the minimum degree of a super vertex-magic total graph must be at least 2. Thus, immediately from this we have that no -crown with cycle of order , i.e., , and thus no , is simultaneously super vertex-magic total and super edge-antimagic total. On the other hand, it is evident that no simultaneously vertex-magic total and edge-antimagic total graph can contain as an induced subgraph. This means that if an -crown with the cycle of order , i.e., , is a simultaneously vertex-magic total and edge-antimagic total graph, then . Thus we state the following for further investigation.

Open Problem 3

For the sun graph , , determine if there exists a total labeling which is simultaneously vertex-magic total and edge-antimagic total.

For prism we showed that for every odd , and , the prism is simultaneously super edge-magic total and super vertex-antimagic total. For prism , when and is odd or is even, we did not find any total labeling with required properties. Therefore we propose the following open problem.

Open Problem 4

For the prism , or even, find a total labeling which is simultaneously super edge-magic and super vertex-antimagic.

For further investigation we also state the following open problem.

Open Problem 5

For the prism , , determine if there exists a total labeling which is simultaneously super vertex-magic and super edge-antimagic.

Notes

Peer review under responsibility of Kalasalingam University.