On some properties of doughnut graphs

Peer review under responsibility of Kalasalingam University.

Abstract

The class of doughnut graphs is a subclass of 5-connected planar graphs. It is known that a doughnut graph admits a straight-line grid drawing with linear area, the outerplanarity of a doughnut graph is 3, and a doughnut graph is -partitionable. In this paper we show that a doughnut graph exhibits a recursive structure. We also give an efficient algorithm for finding a shortest path between any pair of vertices in a doughnut graph. We also propose a nice application of a doughnut graph based on its properties.

Keywords:

• Planar graphs
• Recursive structure
• Hamiltonian
• Fault tolerance
• Connectivity

1 Introduction

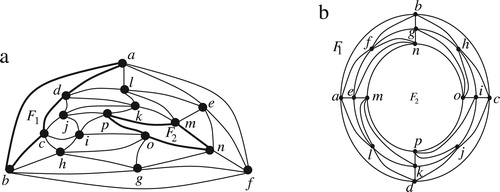
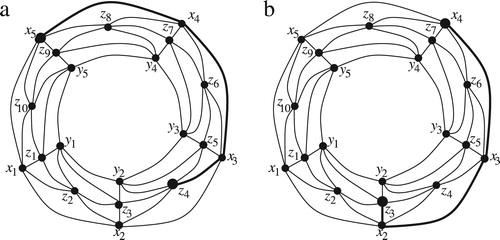
A five-connected planar graph is called a doughnut graph if has an embedding such that (a) has two vertex-disjoint faces each of which has exactly vertices, , and all the other faces of has exactly three vertices; and (b) has the minimum number of vertices satisfying condition (a). Fig. 1(a) illustrates a doughnut graph where and are two vertex disjoint faces. Faces and are depicted by thick lines. The name of doughnut graph was chosen in [1] for such a graph since the graph has a doughnut like embedding, as illustrated in Fig. 1(b). The class of doughnut graphs is an interesting class of graphs which was recently introduced in graph drawing literature for it’s beautiful area-efficient drawing properties [1–^[2]3]. A doughnut graph admits a straight-line grid drawing with linear area [1,3]. Any spanning subgraph of a doughnut graph also admits straight-line grid drawing with linear area [2,3]. The outerplanarity of this class is 3 [3].

Fig. 1 (a) A doughnut graph , and (b) doughnut embedding of .

Given a graph , natural numbers , , , such that , we wish to find a -partition of the vertex set such that and induces a connected subgraph of for each . The problem of finding a -partition of a given graph often appears in the load distribution among different power plants and the fault-tolerant routing of communication networks [4,5]. A doughnut graph is -partitionable [6].

A class of graph has recursive structure if every instance of it can be created by connecting the smaller instances of the same class of graphs. In this paper, we show that any instance of a doughnut graph can be constructed by connecting smaller instances of doughnut graphs. We show that one can find a shortest path between any pair of vertices and of a doughnut graph in time where is the length of shortest path between and by exploiting its beautiful structure. We study the other topological properties like degree, diameter, connectivity and fault tolerance. We show that it’s diameter is . It has maximal fault tolerance, and has ring embedding since it is Hamilton-connected. One may explore the suitability of a doughnut graph as an interconnection network since some of its properties are similar to that of the graph classes usually used for interconnection networks.

The remainder of the paper is organized as follows. In Section 2, we give some definitions and preliminary results. Section 3 provides recursive structure of a doughnut graph. Finding a shortest path between any pair of vertices of doughnut graphs is presented in Section 4. Section 5 summarizes the topological properties of doughnut graphs. Finally Section 6 concludes the paper. An early version of this paper is presented at [7].

2 Preliminaries

In this section we give some definitions.

Let be a connected simple graph with the vertex set and the edge set . Throughout the paper, we denote by the number of vertices in , that is, , and denote by the number of edges in , that is, . An edge joining the vertices and is denoted by . The degree of a vertex , denoted by , is the number of edges incident to in . We denote by the maximum of the degrees of all vertices in . is called r-regular if every vertex of has degree . We call a vertex a neighbor of a vertex in if has an edge . The connectivity of a graph is the minimum number of vertices whose removal results in a disconnected graph or a single-vertex graph . is called - if . A path in is an ordered list of distinct vertices such that for all . The vertices and are the end-vertices of the path . The length of a path is one less than the number of vertices on the path. A path is called a u,v-path if its two end-vertices are and , respectively. The shortest path between two vertices and of is a -path of with the least length. The distance from to , denoted by , is the length of a shortest -path. The diameter of is .

A graph is planar if it can be embedded in the plane so that no two edges intersect geometrically except at a vertex to which they are both incident. A plane graph is a planar graph with a fixed embedding. A plane graph divides the plane into connected regions called . Each of the bounded regions is called an inner face and the unbounded region is called the outer face. Let be all the vertices in the clockwise order on the contour of a face in . We often denote by . For a face in we denote by the set of vertices of on the boundary of face . We call two faces and vertex-disjoint if .

A maximal planar graph is one to which no edge can be added without losing planarity. Thus in any embedding of a maximal planar graph with , each faces of is triangulated, and hence an embedding of a maximal planar graph is a triangulated plane graph. It can be derived from the Euler’s formula for planar graphs that if is a maximal planar graph with vertices and edges then , for more details see [8].

Let be a 5-connected planar graph, let be any planar embedding of and let be an integer such that . We call a - graph if the following Conditions () and () hold: () has two vertex-disjoint faces each of which has exactly vertices, and all the other faces of have exactly three vertices; and () has the minimum number of vertices satisfying Condition (). In general, we call a -doughnut graph for a doughnut graph. The following result is known for doughnut graphs [1].

Lemma 1

Let be a -doughnut graph. Then is 5-regular and has exactly vertices. Furthermore, has three vertex-disjoint cycles , and with , and vertices, respectively, such that .

For a cycle in a plane graph , we denote by the plane subgraph of inside excluding . Let , and be the three vertex-disjoint cycles of a -doughnut graph with , and vertices, respectively, such that . Then we call a planar embedding of a doughnut embedding of if is the outer face and is an inner face of , contains and contains . We call the outer cycle, the middle cycle and the inner cycle of . Fig. 2(b) illustrates the doughnut embedding of the doughnut graph in Fig. 2(a).

Fig. 2 (a) A -doughnut graph where , and (b) doughnut embedding of .

The following results on doughnut embeddings are known for doughnut graphs [1].

Lemma 2

A -doughnut graph always has a doughnut embedding.

Lemma 3

Let be a doughnut embedding of a -doughnut graph and let , and be the outer cycle, the middle cycle and the inner cycle of , respectively. Then either condition (a) or condition (b) holds for any vertex of .

(a)	The vertex has exactly two consecutive neighbors on and exactly one neighbor on .

(b)	The vertex has exactly two consecutive neighbors on and exactly one neighbor on .

Furthermore, for any two consecutive vertices and on , if holds condition (a) then holds condition (b) or vice-versa.

Before going further we need some definitions. Let be a doughnut embedding of and let , and be the outer cycle, middle cycle and the inner cycle of , respectively. Let be a vertex on . Without loss of generality, by Lemma 3 we assume that has exactly two consecutive neighbors on . Let and be the two neighbors of on such that is the counter clockwise next vertex to on . We call the left neighbor of on and the right neighbor of on . Similarly we define the left neighbor and the right neighbor of on if a vertex on has two neighbors on . Let , be the vertices of in counter clockwise order such that has exactly one neighbor on . Let be the neighbor of on , and let , be the vertices of in the counter clockwise order. Let , be the vertices on in counter clockwise order such that and are the right neighbor and the left neighbor of , respectively. Fig. 2(b) illustrates the labeling of vertices of a doughnut embedding of in Fig. 2(a) as mentioned above. In the rest of the paper, we consider a doughnut embedding of a doughnut graph such that the vertices of cycles , and are labeled as mentioned above. We now have the following lemmas from [1].

Lemma 4

Let be a -doughnut graph and let be a doughnut embedding of . Let be a vertex of . Then the following conditions hold.

(a)	The vertex has exactly two neighbors on and exactly one neighbor on if is even. The neighbors of on are and in a counter clockwise order if , otherwise the neighbors of on are and in a counter clockwise order. The neighbor of on is .

(b)	The vertex has exactly two neighbors on and exactly one neighbor on if is odd. The neighbors of on are and in a counter clockwise order if , otherwise the neighbors of on are and in a counter clockwise order. The neighbor of on is .

Lemma 5

Let be a -doughnut graph and let be a doughnut embedding of . Let be a vertex of . Then has exactly three neighbors on in a counter clockwise order if , otherwise has exactly three neighbors , , on in a counter clockwise order.

Lemma 6

Let be a -doughnut graph and let be a doughnut embedding of . Let be a vertex of . Then has exactly three neighbors , , in a counter clockwise order if , otherwise has exactly three neighbors , , on in a counter clockwise order.

3 Recursive structure of doughnut graphs

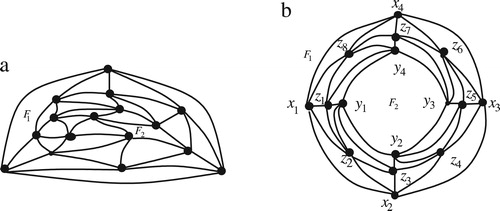
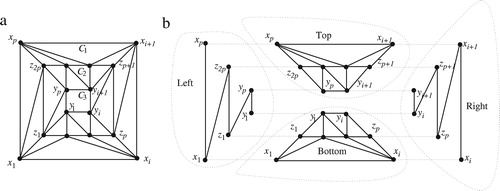
A class of graphs has a recursive structure if every instance of it can be created by connecting the smaller instances of the same class of graphs. We now show that the doughnut graphs have a recursive structure. We now need some definitions. Let be a straight-line grid drawing of a -doughnut graph with linear area as illustrated in Fig. 3(a). We partition the edges of as follows. The left partition consists of the edges—(i) (), (ii) (), (iii) (), (iv)() and (v) (); and the right partition consists of the edges—(i) (), (ii) the edge between the two neighbors of on if has two neighbors on otherwise the edge between the two neighbors of on , (iii) the edge between the two neighbors of on if has two neighbors on otherwise the edge between the two neighbors of on , (iv) the edge between and its right neighbor on if has two neighbors on otherwise the edge between and its left neighbor on , and (v) the edge between and its right neighbor on if has two neighbors on otherwise the edge between and its left neighbor on . The graph is divided into two connected components if we delete the edges of the left and the right partitions from . We call the connected component that contains vertex the top partition of edges and we call the connected component that contains vertex the bottom partition of edges. Fig. 3(b) illustrates four partitions of edges (indicated by dotted lines) of a -doughnut graph in Fig. 3(a) where .

Fig. 3 (a) A doughnut embedding of a -doughnut graph where , and (b) illustration for four partition of edges of .

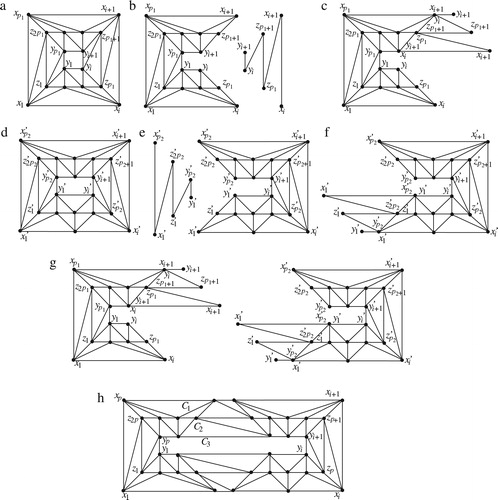
We now construct a ()-doughnut graph from a -doughnut graph and a -doughnut graph . We first construct two graphs and from and , respectively, as follows. We partition the edges of into left, right, top and bottom partitions. Then we identify the vertex of the top partition to the vertex of the right partition, the vertex of the top partition to the vertex of the right partition, and the vertex of the top partition to the vertex of the right partition. Thus we construct from . Fig. 4(c) illustrates which is constructed from in Fig. 4(a) where . In case of construction of , after partitioning (left, right, top, bottom) the edges of we identify the vertex of left partition to the vertex of the bottom partition, vertex of the left partition to the vertex of the bottom partition, and the vertex of left partition to the vertex . Fig. 4(f) illustrates which is constructed from in Fig. 4(d) where . We finally construct a -doughnut graph as follows. We identify the vertices , , of to the vertices of , , of , respectively; and identify the vertices of , , of to the vertices of , , of , respectively. Clearly the resulting graph is a ()-doughnut graph as illustrated in Fig. 4(h).

Fig. 4 Illustration for construction of a ()-doughnut graph from a -doughnut graph and a -doughnut graph where and .

We thus have the following theorem.

Theorem 1

Let be a -doughnut graph and let be a -doughnut graph. Then one can construct -doughnut graph from and .

4 Finding a shortest path

In this section, we present a simple efficient algorithm to find a shortest path between any pair of vertices. We have the following theorem.

Theorem 2

Let be a -doughnut graph and let be a doughnut embedding of . Let , and be the three vertex disjoint cycles of such that is the outer cycle, is the middle cycle and is the inner cycle. Then the shortest path between any pair of vertices and of can be found in time where is the length of the shortest path between and .

To prove the theorem, we need the following lemmas.

Lemma 7

Let be a -doughnut graph and let be a doughnut embedding of . Let , and be the three vertex disjoint cycles of such that is the outer cycle, is the middle cycle and is the inner cycle. Then the shortest path between any two vertices on () contains only the vertices of ( ), respectively.

Proof

We only prove for the case where both of the vertices are on since the proof is similar if both of the vertices are on . Let and be two vertices of . For contradiction, we assume that is a shortest path between and which contains vertices other than the vertices of cycle . Then (i) would have a non-triangulated face other than and or (ii) a vertex of would have degree more than five or (iii) the graph would be non-planar, a contradiction to the properties of a doughnut graph. Therefore the shortest path between any two vertices of contains only the vertices of .  ■

Lemma 8

Let be a -doughnut graph and let be a doughnut embedding of . Let , and be the outer, the middle and the inner cycle of , respectively. Let and be two non-adjacent vertices on and the length of the shorter (between clockwise and counter clockwise) path between them along is . Then the length of any path between and is at least .

Proof

Without loss of generality we assume that and the shortest path between and along is in the counter clockwise direction. We prove the claim by induction on . Since and are non-adjacent, then . The claim is true for where , and the shortest path between these two vertices has length .

Assume that and the claim is true for all pairs of vertices of with the shorter distance between them along . In this case . Let be any path between and . We now show that the length of is at least .

We first consider the case where contains some vertex of cycle such that . If is adjacent to , then by induction hypothesis, the length of any path between and has length and therefore the length of is at least . From the same line of reasoning, we can show that if is adjacent to , then the length of is at least . Thus we assume that is adjacent to neither nor . Then from induction hypothesis, the length of any path between and is at least and the length of any path between and is at least . Therefore the length of is at least . Hence, no path containing vertices of the cycle other than and has length less than .

Thus we assume that does not contain any vertices of other than and . Therefore there are only two different paths to consider for each pair of vertices and , one containing only vertices of and the other containing only vertices of other than and . If contains only the vertices of other than and , then by Lemma 4, the rightmost (or only) neighbor of and the leftmost (or only) neighbor of on are and , respectively. Therefore the length of is at least as illustrated in Fig. 5(a) and (b). On the other hand, if contains only the vertices of other than and , then by Lemma 4, the rightmost (or only) neighbor of and the leftmost (or only) neighbor of on are and , respectively. Therefore the length of is at least as illustrated in Fig. 5(c) and (d).  ■

Fig. 5 Illustration of shortest path between two vertices on of a doughnut graph.

We are now ready to prove Theorem 2.

Proof

The vertices of lie on three vertex disjoint cycles , and where is the outer cycle, is the middle cycle and is the inner cycle. We have four cases to consider.

Case 1: Both and are either on or on .

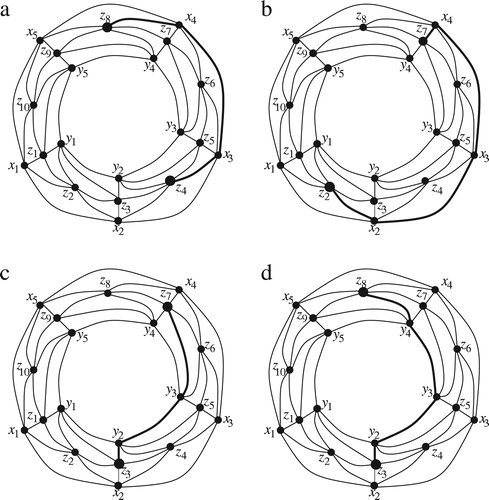
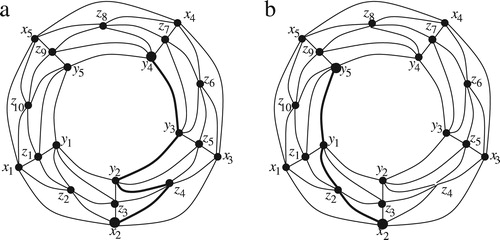
Without loss of generality, we assume that both the and are on , since the case is similar where both of and are on . Let and . Without loss of generality, we may assume that . Let us take the path , , , if otherwise , , ,. By Lemma 7, is the shortest path between and . Fig. 6 illustrates the case where (i) and , and (ii) and .

Case 2: Both and are on .

We assume that and , respectively. The shortest path between and consists of edge if and are adjacent. We thus assume that and are not adjacent. Without loss of generality, we also assume that . We now define a path between and . We have the following four types of paths to consider — (i) we take path if both and are even; (ii) we take path if both and are odd; (iii) we take path if is even and is odd; (iv) we take path if is odd and is even. The paths of Types (i), (iii) and (iv) contain vertices of and . By Lemma 4, and are neighbors of and by Lemma 5, is a neighbor of and . The path of Type (ii) contains vertices of and . By Lemma 4, is a neighbor of and by Lemma 6, is a neighbor of . It is easy to verify that each of the paths as mentioned above has length and by Lemma 8, these paths are the shortest paths between and .

Case 3: One of and is on , and the other one is on or .

We assume that is on and the is on . Let and . We also assume that . For odd value of , we take , , if otherwise , , . For even value of , we take , , if otherwise , , . Each of the paths contain vertices of and . By Lemma 4, and are neighbors of . We can prove that both of the paths are the shortest path since each of them are the subpaths of the shortest path of Subcase 2(b) and the length of the shortest path between and is . Fig. 7(a) illustrates an example where and . The shortest path , , , . Fig. 7(b) illustrates an example where and . The shortest path , , , .

Case 4: One of and is on , and the other one is on .

We assume that is on and is on . Let and . Without loss of generality, we assume that . Let us take the path , , , if otherwise let us take path , , , . Each of the paths contain vertices of , and . By Lemma 5, and are neighbors of , and by Lemma 4, is a neighbor of and is a neighbor of . We now prove that is the shortest path between and . We prove only for the case where is to the counter clockwise direction of . Let . Since the length of is , it is sufficient to prove that the length of the shortest path between and is at least . The claim is obvious for . We thus assume that and the claim is true for any value of . Assume for contradiction that there is a shortest path between and with length less than . Since is to counter clockwise direction from , the second vertex of the shortest path is either or . If is the second vertex then by induction hypothesis, the shortest path between and has length and the length of is at least which contradicts our assumption. Thus we assume that the second vertex is . 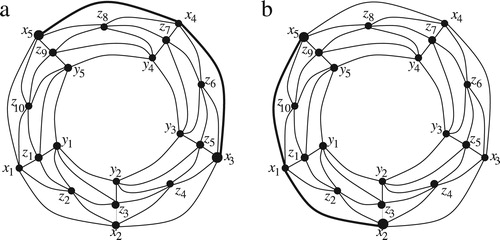Since contains the shortest path between and by Case 3, the length of cannot be less than in this case also. Fig. 8(a) illustrates an example where and . The shortest path , , , , . Fig. 8(b) illustrates an example where and . The shortest path , , , .

Thus we can find a shortest path between any pair of vertices of a doughnut graph. One can see that the shortest path between any pair of vertices can be found in time where is the length of the shortest path between and .  ■

Fig. 6 Illustration for Case 1.

Fig. 7 Illustration for case 3.

Fig. 8 Illustration for Case 4.

5 Topological properties of doughnut graphs

Let be a -doughnut graph. By Lemma 1, the number of vertices of is where is an integer. A -doughnut graph is maximal fault tolerant since it is 5-regular by Lemma 1. By Lemma 2, every -doughnut graph has a doughnut embedding where vertices of lie on three vertex disjoint cycles , and such that is the outer cycle containing vertices, is the middle cycle containing vertices and is the inner cycle containing vertices. Then one can easily see that the diameter of a -doughnut graph is . Moreover, a doughnut graph admits a ring embedding since a doughnut graph is Hamilton-connected [6].

6 Conclusion

In this paper, we have studied recursive structure of doughnut graphs. We have proposed an efficient algorithm to find shortest path between any pair of vertices which exploit the structure of the graph. We have also found that doughnut graph has smaller diameter, higher degree and connectivity, maximal fault tolerance and ring embedding. There are several parameters like connectivity, degree, diameter, symmetry and fault tolerance which are considered for building interconnection networks [9]. Table 1 presents the topological comparison of various Cayley graphs, which are widely used as interconnection networks, with doughnut graphs. The table shows that topological properties of doughnut graphs are very much similar to interconnection networks. One of the limitation is the diameter which is linear but the coefficient is . We may have an efficient routing scheme using shortest path finding algorithm. We can have a scalable interconnection network using doughnut graphs since the degree of a vertex of a doughnut graph does not change with the size of the graph. This is also important for VLSI implementation point of view as well as applications where the computing nodes in an interconnection networks only have fixed number of I/O ports. Thus doughnut graphs may find nice applications as interconnection networks.

Table 1 Topological comparison of doughnut graphs with various Cayley graphs.

Topology	Number of nodes	Diameter	Degree	Connectivity	Fault tolerance	Hamiltonian
-cycle			2	2	Maximal	Yes
Cube-connected-cycle [10]			3	3	Maximal	Yes
Wrapped around butterfly graph [11]			4	4	Maximal	Yes
-Dimensional hypercube [12]					Maximal	Yes
-doughnut graphs [1]			5	5	Maximal	Yes

Notes

Peer review under responsibility of Kalasalingam University.