L(3,2,1)- and L(4,3,2,1)-labeling problems on interval graphs

Peer review under responsibility of Kalasalingam University.

Abstract

For a given graph $G=(V,E)$, the $L(3,2,1)$- and $L(4,3,2,1)$-labeling problems assign the labels to the vertices of $G$. Let $Z^{\ast }$ be the set of non-negative integers. An $L(3,2,1)$- and $L(4,3,2,1)$-labeling of a graph $G$ is a function $f:V\to Z^{\ast }$ such that $|f\left(x\right)-f\left(y\right)|\ge k-d(x,y)$, for $k=4,5$ respectively, where $d(x,y)$ represents the distance (minimum number of edges) between the vertices $x$ and $y$, and $1\le d(x,y)\le k-1$. The $L(3,2,1)$- and $L(4,3,2,1)$-labeling numbers of a graph $G$, are denoted by ${\lambda }_{3,2,1}\left(G\right)$ and ${\lambda }_{4,3,2,1}\left(G\right)$ and they are the difference between highest and lowest labels used in $L(3,2,1)$- and $L(4,3,2,1)$-labeling respectively. In this paper, for an interval graph $G$, it is shown that ${\lambda }_{3,2,1}\left(G\right)\le 6\Delta -3$ and ${\lambda }_{4,3,2,1}\left(G\right)\le 10\Delta -6$, where $\Delta$ represents the maximum degree of the vertices of $G$. Also, two algorithms are designed to label an interval graph by maintaining $L(3,2,1)$- and $L(4,3,2,1)$-labeling conditions. The time complexities of both the algorithms are $O\left(n{\Delta }^2\right)$, where $n$ represent the number of vertices of $G$.

Keywords:

• Frequency assignment
• $L(3,2,1)$-labeling
• $L(4,3,2,1)$-labeling
• Interval graphs

1 Introduction

The frequency assignment problem is a problem where the task is to assign a frequency (non-negative integer) to a given group of televisions or radio transmitters so that interfering transmitters are assigned frequency with at least a minimum allowed separation. A frequency assignment problem is motivated from the distance labeling problem of graphs. It is to find a proper assignment of channels to transmitters in a wireless network. The level of interference between any two radio stations correlates with the geographic locations of the stations. Closer stations have a stronger interference and thus there must be a greater difference between there assigned channels.

Table

Vertices	$I_1$	$I_2$	$I_3$	$I_4$	$I_5$	$I_6$	$I_7$	$I_8$	$I_9$	$I_{10}$	$I_{11}$	$I_{12}$	$I_{13}$
$L(3,2,1)$-labels	$0$	$3$	$6$	$9$	$1$	$4$	$7$	$10$	$0$	$13$	$3$	$6$	$1$

Table

Vertices	$v_1$	$v_2$	$v_3$	$v_4$	$v_5$	$v_6$	$v_7$	$v_8$	$v_9$	$v_{10}$	$v_{11}$	$v_{12}$	$v_{13}$
$L(4,3,2,1)$-labels	$0$	$4$	$8$	$12$	$16$	$1$	$5$	$9$	$13$	$18$	$3$	$7$	$11$

The frequency assignment problem was formulated as a vertex colouring problem of graph by Hale [1]. In, 1988, Roberts proposed a variation of the frequency assignment problem in which ‘closed’ transmitter must receive different frequency and ‘very closed’ transmitter must receive a frequency at least two apart. Two vertices $x$ and $y$ are said to be ‘very closed’ and ‘closed’ if the distance between $x$ and $y$ is $1$ and $2$ respectively. Griggs and Yeh [2] defined the $L(2,1)$-labeling of a graph $G=(V,E)$ as a function $f$ from the vertex set $V\left(G\right)$ to the set of non-negative integers such that $|f\left(x\right)-f\left(y\right)|\ge 2$ if $d(x,y)=1$ and $|f\left(x\right)-f\left(y\right)|\ge 1$ if $d(x,y)=2$, where $d(x,y)$ represent the distance between the vertices $x$ and $y$. The minimum span over all possible labeling functions of $L(2,1)$-labeling is denoted by ${\lambda }_{2,1}\left(G\right)$ and is called ${\lambda }_{2,1}$ number of $G$.

Similarly, an $L(3,2,1)$-labeling of a graph $G$ is a function $f$ from its vertex set $V$ to the set of non-negative integers such that $|f\left(x\right)-f\left(y\right)|\ge 3$ if $d(x,y)=1$, $|f\left(x\right)-f\left(y\right)|\ge 2$ if $d(x,y)=2$ and $|f\left(x\right)-f\left(y\right)|\ge 1$ if $d(x,y)=3$. The $L(3,2,1)$-labeling number, ${\lambda }_{3,2,1}\left(G\right)$, of $G$ is the smallest non-negative integer $k$ such that $G$ has a $L(3,2,1)$-labeling of span $k$. Also, an $L(4,3,2,1)$-labeling of a graph $G$ is a function $f$ from its vertex set $V$ to the set of non-negative integers such that $|f\left(x\right)-f\left(y\right)|\ge 4$ if $d(x,y)=1$, $|f\left(x\right)-f\left(y\right)|\ge 3$ if $d(x,y)=2$, $|f\left(x\right)-f\left(y\right)|\ge 2$ if $d(x,y)=3$ and $|f\left(x\right)-f\left(y\right)|\ge 1$ if $d(x,y)=4$. The $L(4,3,2,1)$-labeling number, ${\lambda }_{4,3,2,1}\left(G\right)$, of $G$ is the smallest non-negative integer $k$ such that $G$ has a $L(4,3,2,1)$-labeling of span $k$. Frequency assignment problem has been widely studied in the past [3–6^[3][4][5][6]]. In 2007, Bertossi et al. have studied approximate $L({\delta }_1,{\delta }_2,\dots ,{\delta }_t)$-coloring of trees and interval graphs [7] and Bodlaender et al. have studied about approximations for $\lambda$-colorings of graphs [8]. Also in [9], Khan et al. have studied $L(2,1)$-total labeling of cactus graphs and in [10] they studied $L(0,1)$-labeling of cactus graphs. Later Calamoneri [11] studied $L({\delta }_1,{\delta }_2,1)$-labeling of eight grids, Amanathulla and Pal studied $L(3,2,1)$-labeling and $L(4,3,2,1)$-labeling of circular-arc graphs [12]. We focus our attention on $L(3,2,1)$-labeling and $L(4,3,2,1)$-labeling of interval graphs. Different bounds for ${\lambda }_{3,2,1}\left(G\right)$ and ${\lambda }_{4,3,2,1}\left(G\right)$ were obtained for various type of graphs. The upper bound of ${\lambda }_{p,1}\left(G\right)$ of any graph $G$ is ${\Delta }^2-(p-1)\Delta -2$ [13], where $\Delta$ is the degree of the graph. In [14], Clipperton et al. showed that ${\lambda }_{3,2,1}\left(G\right)\le {\Delta }^3+{\Delta }^2+3\Delta$ for any graph. Later Chai et al. [15] improved this upper bound and showed that ${\lambda }_{3,2,1}\left(G\right)\le {\Delta }^3+2\Delta$ for any graph. In [16], Lui and Shao studied the $L(3,2,1)$-labeling of planer graph and showed that ${\lambda }_{3,2,1}\left(G\right)\le 15({\Delta }^2-\Delta +1)$. In [15], Chia et al. also showed that ${\lambda }_{3,2,1}\left(G\right)=2n+5$ if $T$ is a complete $n$-ary tree of height $h\ge 3$ and for any tree $2\Delta +1\le {\lambda }_{3,2,1}\left(G\right)\le 2\Delta +3$. In [17], Jean studied about $L(d,2,1)$-labeling of simple graph and showed that ${\lambda }_{d,2,1}\left(K_n\right)=d(n-1)+1$, where $K_n$ is complete graph with $n$ vertices and also shown that ${\lambda }_{d,2,1}\left(K_{m,n}\right)=d+2(m+n)-3$. Kim et al. [18] show that ${\lambda }_{3,2,1}\left(K_3\square C_n\right)=15$ when $n\ge 28$ and $n\equiv 0\left(mod5\right)$, where $K_3\square C_n$ is the Cartesian product of complete graphs $K_3$ and the cycle $C_n$. Again, Clipperton [19] have shown that ${\lambda }_{4,3,2,1}\left(G\right)\le {\Delta }^3+2{\Delta }^2+6\Delta$ for any graph $G$. In [20], Paul et al. showed that ${\lambda }_{2,1}\left(G\right)\le \Delta +w$ for interval graph and they also shown that ${\lambda }_{2,1}\left(G\right)\le \Delta +3w$ for circular-arc graph, where $w$ represents the size of the maximum clique, also in [21] they have shown that the value of ${\lambda }_{0,1}$ can be computed for interval graph using polynomial time. Recently, Paul et al. have studied a linear time algorithm to compute square of interval graphs and their colouring [22]. Calamoneri et al. [23] have shown that ${\lambda }_{0,1}\left(G\right)\le 2\Delta$ and ${\lambda }_{1,1}\left(G\right)\le 2\Delta +\omega$ for circular-arc graphs. Also in [12], Amanathulla and Pal have shown that ${\lambda }_{0,1}\left(G\right)\le \Delta$ and ${\lambda }_{1,1}\left(G\right)\le 2\Delta$ for circular-arc graphs and they have also shown that ${\lambda }_{3,2,1}\left(G\right)\le 9\Delta -6$, ${\lambda }_{4,3,2,1}\left(G\right)\le 16\Delta -12$ for circular-arc graphs [24] and ${\lambda }_{3,2,1}\left(G\right)\le 11\Delta -8$ if $\Delta \le 5$ and ${\lambda }_{3,2,1}\left(G\right)\le 13\Delta -18$ if $\Delta >5$ for permutation graphs [25].

In this paper, for interval graphs $G$, it is shown that the upper bounds of $L(3,2,1)$- and $L(4,3,2,1)$-labeling are $6\Delta -3$ and $10\Delta -6$ respectively, where $\Delta$ represents the maximum degree of the vertices. Also two algorithms are designed to label an interval graph by $L(3,2,1)$- and $L(4,3,2,1)$-labeling. The time complexities of both the algorithms are $O\left(n{\Delta }^2\right)$, where $n$ represent the number of vertices of $G$.

The remaining part of the paper is organized as follows. Some notations and definitions are presented in Section 2. In Section 3, some lemmas related to our work and an algorithm to $L(3,2,1)$-label an interval graphs are presented. Section 4 is devoted to $L(4,3,2,1)$-labeling problem of interval graphs. In Section 5, a conclusion is made.

2 Preliminaries and notations

The graphs used in this work are simple, finite, without self loop or multiple edges. A graph $G=(V,E)$ is called an intersection graph for a finite family $F$ of a non-empty set if there is a one-to-one correspondence between $F$ and $V$ such that two sets in $F$ have non-empty intersection if and only if there corresponding vertices in $V$ are adjacent to each other. We call $F$ an intersection model of $G$. For an intersection model $F$, we use $G\left(F\right)$ to denote the intersection graph for $F$. Depending on the nature of the set $F$ one gets different intersection graphs. The class of interval graph is a very important subclass of intersection graph [26–28^[26][27][28]]. In [29] Pal et al. discussed, a data structure on interval graphs and its applications. Let $I=\{I_1,I_2,\dots ,I_n\}$, where $I_k=[a_k,b_k],k=1,2,\dots ,n$ be a set of intervals on a real line, $a_j$ and $b_j$ are respectively the left and right end points of the interval $I_k$. We draw a vertex $v_k$ for the interval $I_k,k=1,2,\dots ,n$. Two vertices $v_i$ and $v_j$ are adjacent if and only if there corresponding intervals have non empty intersection. Thus an undirected graph $G=(V,E)$ is an interval graph if the vertex set $V$ can be put into one-to-one correspondence with a set of intervals $I$ on the real line such that two vertices are adjacent in $G$ if and only if there corresponding intervals have non empty intersection. Also, it is observed that an interval $I_k$ of $I$ and a vertex $v_k$ of $V$ are one and same thing. We assume that the intervals in $I$ are indexed by increasing left end points, that is, $a_1<a_2<\cdots <a_n$, i.e. $v_1<v_2<\cdots <v_n)$. 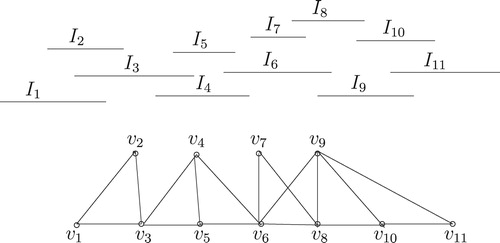This indexing is known as $IG$ ordering. An interval representation and its corresponding interval graphs are shown in Fig. 1.

Fig. 1 An interval representation and the corresponding interval graph.

For any interval graph $G$ and its interval representation $I$, we define the following notations:

1.	$L\left(I_k\right)$: the set of used labels before labeling the interval $I_k$, for any $I_k\in I$.

2.	$L_i\left(I_k\right)$: the set of used labels at distance $i$ ($i=1,2,3,4$) from the interval $I_k$, before labeling the interval $I_k$, for any $I_k\in I$.

3.	$L_{vl}(i,I_k)$: the set of all valid labels to label the interval $I_k$ before labeling $I_k$, satisfying the condition of distance $i,i-1$ and $i-2$, for $i=1,2,3$ of $L(3,2,1)$-labeling, for any $I_k\in I$.

4.	$L_{vl}^{\prime }(i,I_k)$: the set of all valid labels to label the interval $I_k$ before labeling $I_k$, satisfying the condition of distance $i,i-1,i-2$ and $i-3$, for $i=1,2,3,4$ of $L(4,3,2,1)$-labeling, for any $I_k\in I$.

5.	$f_j$: the label of the interval $I_j$, for any $I_j\in I$.

6.	$L$: the label set, i.e. the set of labels used to label the interval graph $G$ completely.

3 $L(3,2,1)$-labeling of interval graphs

In this section, we introduced some results which are used to find the upper bound of $L(3,2,1)$-labeling. Also, these results are used to design the algorithm.

Lemma 1

For an interval graph $G$, $\left|L_i\left(I_k\right)\right|\le \Delta -1$, $i=2,3,4$ for any interval $I_k\in I$ of $G$.

Proof

Let $G$ be an interval graph. we start the labeling of the graph from the leftmost interval. Let $v_k$ be the vertex of the graph $G$ corresponding to the interval $I_k$. We consider a situation in which the intervals $I_1,I_2,\dots ,I_{k-1}$ (for $k=2,3,\dots ,n$) are already labeled by $L(3,2,1)$-labeling and the remanning intervals are not labeled.

Case 1:$i=2$

Let $\left|L_2\left(I_k\right)\right|=m$. This implies that $m$ distinct labels are used to label the intervals at distance two from the interval $I_k$, before labeling the interval $I_k$.

Since, $G$ is an interval graph and $\Delta$ be the degree of the graph $G$, so there exists an interval $I_{\alpha }$ (in Fig. 2) which is adjacent to at most $\Delta$ intervals of $G$. In Fig. 2, $I_{\alpha }$ is adjacent to $I_k,I_{\beta },I_{k_{21}},I_{k_{22}},I_{k_{23}}$. Among the intervals, some intervals ($I_{\beta },I_{k_{21}},I_{k_{22}},I_{k_{23}}$ in Fig. 2) are of distance two from $I_k$ and among these intervals at least one interval ($I_k$ in Fig. 2) is not at distance two from $I_k$. Therefore, $m\le \Delta -1$, i.e. $\left|L_2\left(I_k\right)\right|\le \Delta -1$.

Case 2:$i=3$

Let $\left|L_3\left(I_k\right)\right|=p$. This implies that $p$ distinct labels are used to label the intervals at distance three from the interval $I_k$, before labeling the interval $I_k$. Since, $G$ is an interval graph, so among the intervals at distance two from $I_k$, there exists an interval $I_{\beta }$ (in Fig. 2) which is adjacent to at most $\Delta$ intervals ($I_{\alpha },I_{k_{21}},I_{k_{22}},I_{k_{23}},I_{k_{31}},I_{k_{32}},I_{k_{33}}$) of $G$. Among these intervals some intervals ($I_{k_{31}},I_{k_{32}},I_{k_{33}}$ in Fig. 2) are of distance three from the interval $I_k$. And also among the intervals there exists at least one interval ($I_{\alpha }$ in Fig. 2) which is adjacent to $I_{\beta }$ but not at distance three from $I_k$. So, $p\le \Delta -1$. Hence, $\left|L_3\left(I_k\right)\right|\le \Delta -1$.

Case 3:$i=4$

This case is similar to the previous cases. □

Fig. 2 A set of intervals.

Lemma 2

For any interval graph $G$, $L_i\left(I_k\right)\subseteq L\left(I_k\right)$, for any interval $I_k\in I$, $i=1,2,3,4$.

Proof

According to the definition, $L\left(I_k\right)$ is the set of used labels before labeling the interval $I_k$. So any label $l\in L_i\left(I_k\right)$ implies $l\in L\left(I_k\right)$, for $i=1,2,3,4$. Hence $L_i\left(I_k\right)\subseteq L\left(I_k\right)$. □

Theorem 1

For any interval graph $G$, the $L(3,2,1)$-labeling number ${\lambda }_{3,2,1}\left(G\right)$ is at most $6\Delta -3$, where $\Delta$ is the degree of the graph $G$.

Proof

Let the number of vertices of the graph $G$ be $n$ and let $I=\{I_1,I_2,\dots ,I_n\}$, where $I_k$ is the interval corresponding to the vertex $v_k$ of the graph $G$. We shall label the intervals in ascending order of their subscripts.

Let $L\left(I_k\right)=\{0,1\dots ,6\Delta -3\}$, where $I_k\in I$. Then $\left|L\left(I_k\right)\right|=6\Delta -2$. If the set $L\left(I_k\right)$ is sufficient to label all the intervals corresponding to all the vertices of the graph $G$ satisfying $L(3,2,1)$-labeling condition, then we can say that ${\lambda }_{3,2,1}\left(G\right)\le 6\Delta -3$. We consider a situation in which the intervals $I_1,I_2,\dots ,I_{k-1}$, for $k=2,3\dots ,n$ are already labeled and $I_k,I_{k+1},\dots ,I_n$ are not labeled. In this case, we want to label the interval $I_k$. We know that $\left|L_1\left(I_k\right)\right|\le \Delta$. So, in worst case $(6\Delta -2)-3\Delta =3\Delta -2$ labels of the set $L\left(I_k\right)$ are available, which satisfies the condition of distance one of $L(3,2,1)$-labeling.

Also, since, $\left|L_2\left(I_k\right)\right|\le \Delta -1$ (By Lemma 1), so in worst case $(3\Delta -2)-2(\Delta -1)=\Delta$ labels of the set $L\left(I_k\right)$ are available, which satisfies the condition of distance one and two of $L(3,2,1)$-labeling. Again, since, $\left|L_3\left(I_k\right)\right|\le \Delta -1$ (By Lemma 1), so in the extreme unfavourable cases at least one (viz. $\Delta -(\Delta -1)=1$) label of the set $L\left(I_k\right)$ is available satisfying $L(3,2,1)$-labeling condition. Since $I_k$ is arbitrary so we can label any interval of the interval graph $G$ satisfying $L(3,2,1)$-labeling condition by using only the label of the set $L\left(I_k\right)$. If we take $L\left(I_k\right)$ so that $L\left(I_k\right)\subset \{0,1\dots ,6\Delta -3\}$ and in similar manner we are going to label the interval $I_k$ by $L(3,2,1)$-labeling, then it follows that the set $L\left(I_k\right)$ may or may not contain a label satisfying $L(3,2,1)$-labeling condition. Therefore, ${\lambda }_{3,2,1}\left(G\right)\le 6\Delta -3$. Hence, the $L(3,2,1)$-labeling number for interval graph is at most $6\Delta -3$. □

3.1 Algorithm for $L(3,2,1)$-labeling

In this section, we design an algorithm to compute the set $L_{vl}(k,I_j)$ for $j=2,3,\dots ,n$ and $k=1,2,3$ and also we design an algorithm to $L(3,2,1)$-label an interval graph. We consider a situation in which some intervals (the intervals $I_k$’s with index $k<j$) are labeled by $L(3,2,1)$-labeling and some intervals (the intervals $I_k$’s with index $k\ge j$) are not labeled.

Lemma 3

Algorithm $LKVL$, $k=1,2,3$ correctly compute $L_{vl}(k,I_j)$ for $j=2,3,\dots ,n$ and the running time for this algorithm is $O\left({\Delta }^2\right)$.

Proof

According to this algorithm every element $i\in L_{vl}(1,I_j)$ is differ from $l_p$ by at least $3$ for each $l_p\in L_1\left(I_j\right)$. So, $|i-l_p|\ge 3$ for all $i\in L_{vl}(1,I_j)$ and for all $l_p\in L_1\left(I_k\right)$. So the algorithm correctly computes $L_{vl}(1,I_j)$.

Again, according to the above algorithm for each $k=1,2$ every element $l_m$ of $L_{vl}(k+1,I_j)$ is differ from $p_n$ by at least $3-k$ for each $p_n\in L_{(k+1)}\left(I_j\right)$. So, $|l_m-p_n|\ge 3-k$ for all $l_m\in L_{vl}(k+1,I_j)$ and for all $p_n\in L_{k+1}\left(I_j\right)$, for $k=1,2$. Hence the algorithm correctly computes $L_{vl}(k,I_j)$ for $k=1,2,3$.

Since $L$ is the label set and $\left|L\right|$ be its cardinality, clearly $\left|L_i\left(I_j\right)\right|\le \left|L\right|$ for $i=1,2,3$ and for any $I_j\in I$ and also $r\le 6\Delta$, where $r=max\left\{L\left(I_j\right)\right\}+3$. So we can compute $L_{vl}(1,I_j)$ using at most $\left|L\right|6\Delta$ times, i.e. using $O\left(\Delta \left|L\right|\right)$ times. Also, $\left|L_{vl}(k,I_j)\right|\le 6\Delta -2$, for $k=1,2$. So for each $k=1,2,L_{vl}(k+1,I_j)$ can be computed using at most $\left|L\right|(6\Delta -2)$ times, i.e. using $O\left(\Delta \left|L\right|\right)$ times. So the time complexity of the algorithm $LKVL$ is $O\left(\Delta \left|L\right|\right)$, i.e. $O\left({\Delta }^2\right)$, since $\left|L\right|\le 6\Delta -2$. □

Lemma 4

For any interval graph $G$ and for any $I_j\in I$, $L_{vl}(k,I_j)$ is the largest non empty set satisfying the condition of distance $1,2,\dots ,k$ for $k=1,2,3$, of $L(3,2,1)$-labeling, where $l\le u$ for all $l\in L_{vl}(k,I_j)$ and $u=max\left\{L\left(I_j\right)\right\}+3$, for any $I_j\in I$ and $k=1,2,3$.

Proof

Since, $u=max\left\{L\left(I_j\right)\right\}+3$ and $L_i\left(I_j\right)\subseteq L\left(I_j\right)$ for $i=1,2,3$ (By Lemma 2), so $|u-l_p|\ge 3$ for any $l_p\in L_i\left(I_j\right),i=1,2,3$. Therefore, $u\in L_{vl}(k,I_j)$ for $k=1,2,3$. Hence, for any $k=1,2,3$, $L_{vl}(k,I_j)$ is non empty. Again, let $A$ be any set of labels satisfying the condition of distance $1,2,\dots ,k$ for $k=1,2,3$, of $L(3,2,1)$-labeling, where $l\le u$ for all $l\in A$. Also, let $a\in A$. Then $|a-l_i|\ge 4-i$ for any $l_i\in L_i\left(I_j\right)$ and for $i=k-2,k-1,k$, where $i>0$. Thus, $a\in L_{vl}(k,I_j)$, for $k=1,2,3$. Therefore, $a\in A$ implies $a\in L_{vl}(k,I_j)$, for $k=1,2,3$. So, $A\subseteq L_{vl}(k,I_j)$, for $k=1,2,3$. Since $A$ is arbitrary, so for any $k=1,2,3$, $L_{vl}(k,I_j)$ is the largest non empty set of labels satisfying the condition of distance $1,2,\dots ,k$ for $k=1,2,3$ of $L(3,2,1)$-labeling, where $l\le u$ and for all $l\in L_{vl}(k,I_j)$. □

Theorem 2

Algorithm $L321$ correctly labels an interval graph satisfying $L(3,2,1)$-labeling condition.

Proof

Let $G$ be an interval graph with $n$ vertices. Let $I=\{I_1,I_2,\dots ,I_n\}$ be the set of intervals of the interval graph, also let $f_1=0$, $L\left(I_2\right)=\left\{0\right\}$. If $n=1$, then $L\left(I_2\right)$ is sufficient to label the whole graph and obviously, ${\lambda }_{3,2,1}\left(G\right)=0$. If $n>1$, then $L\left(I_2\right)$ is not sufficient to label the graph $G$ by $L(3,2,1)$-labeling, because in this case more than one label is required and $L\left(I_2\right)$ contains only one label.

We consider a situation in which the intervals $I_1,I_2,\dots ,I_{j-1}$ are already labeled for $j=2,3,\dots ,n$. In this situations we want to label the interval $I_j$ by $L(3,2,1)$-labeling. We know that $L_{vl}(k,I_j)$ is the largest non-empty set satisfying the condition of distance $1,2,\dots ,k$ for $k=1,2,3$ of $L(3,2,1)$-labeling, where $l\le u$ for all $l\in L_{vl}(k,I_j)$ and $u=max\left\{L\left(I_j\right)\right\}+3$ for any $I_j\in I$ and $k=1,2,3$ (By Lemma $4$). Again, no label $l\le u$ and $l\notin L_{vl}(3,I_j)$ satisfying $L(3,2,1)$-labeling condition. So the labels on the set $L_{vl}(3,I_j)$ is the only valid label for $I_j$, which is less than or equal to $u$ and satisfying $L(3,2,1)$-labeling condition. Since we want to label the interval $I_j$ by $L(3,2,1)$-labeling, so, $f_j=q$, where $q=min\left\{L_{vl}(3,I_j)\right\}$. Then $q$ is the least label for $I_j$, because no label less than $q$ satisfies $L(3,2,1)$-labeling condition. Since, $I_j$ is arbitrary so by Algorithm $L321$ the graph $G$ can be labeled using minimum number of labels satisfying $L(3,2,1)$-labeling condition and ${\lambda }_{3,2,1}\left(G\right)=max\{L\left(I_n\right)\bigcup \left\{f_n\right\}\}$. □

Theorem 3

The time complexity of Algorithm $L321$ is $O\left(n{\Delta }^2\right)$, where $n$ is the number of vertices of the graph and $\Delta$ is the degree of the graph.

Proof

In Algorithm $L321$, our aim is to find least possible label for each interval $I_j$. By our proposed algorithm it is clear that $f_j$ can be computed if $L_{vl}(3,I_j)$ is computed. Now by Lemma 3, Algorithm $LKVL$ for $k=1,2,3$ takes $O\left({\Delta }^2\right)$ time to compute $L_{vl}(3,I_j)$. Since we need to find $L_{vl}(3,I_j)$ for $j=2,3,\dots ,n$, so the overall time complexity of Algorithm $L321$ is $O\left((n-1){\Delta }^2\right)$, i.e. $O\left(n{\Delta }^2\right)$. □

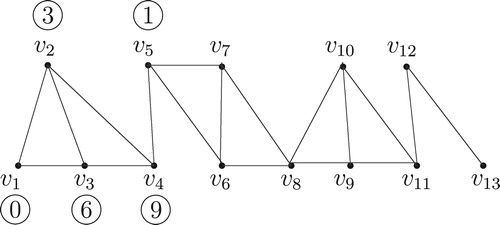
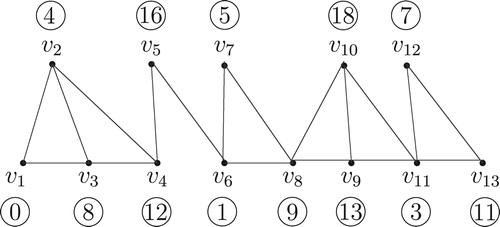
Illustration of Algorithm$L321$

We consider an interval graph with $13$ vertices (see Fig. 3) and labeled this graph by Algorithm $L321$.

Fig. 3 An interval graph labeled by $L(3,2,1)$-labeling, the number within the circle represents the label of the corresponding vertices.

For this graph, $I=\{I_1,I_2,\dots ,I_{13}\}$ and $\Delta =4$.

$f_j=$ the label of the interval $I_j$, for $j=1,2,\dots ,13$.$f_1=0$, $L\left(I_2\right)=\left\{0\right\}$.

Iteration 1: For $j=2$.

$L_1\left(I_2\right)=\left\{0\right\}$, $L_2\left(I_2\right)=\varphi$, $L_3\left(I_2\right)=\varphi$.

$L_{vl}(1,I_2)=\left\{3\right\}$, $L_{vl}(2,I_2)=\left\{3\right\}$, $L_{vl}(3,I_2)=\left\{3\right\}$.

Therefore, $f_2=min\left\{L_{vl}(3,I_2)\right\}=3$ and $L\left(I_3\right)=L\left(I_2\right)\cup \left\{f_2\right\}=\left\{0\right\}\cup \left\{3\right\}=\{0,3\}$.

Iteration 2: For $j=3$.

$L_1\left(I_3\right)=\{0,3\}$, $L_2\left(I_3\right)=\varphi$, $L_3\left(I_3\right)=\varphi$.

$L_{vl}(1,I_3)=\left\{6\right\}$, $L_{vl}(2,I_3)=\left\{6\right\}$, $L_{vl}(3,I_3)=\left\{6\right\}$.

So $f_3=min\left\{L_{vl}(3,I_3)\right\}=6$ and $L\left(I_4\right)=L\left(I_3\right)\cup \left\{f_3\right\}=\{0,3,\}\cup \left\{6\right\}=\{0,3,6\}$.

Iteration 3: For $j=4$.

$L_1\left(I_4\right)=\{0,6\}$, $L_2\left(I_4\right)=\left\{0\right\}$, $L_3\left(I_4\right)=\varphi$.

$L_{vl}(1,I_4)=\{0,9\}$, $L_{vl}(2,I_4)=\left\{9\right\}$, $L_{vl}(3,I_4)=\left\{9\right\}$.

Therefore, $f_4=min\left\{L_{vl}(3,I_4)\right\}=9$ and $L\left(I_5\right)=L\left(I_4\right)\cup \left\{f_4\right\}=\{0,3,6\}\cup \left\{9\right\}=\{0,3,6,9\}$.

Iteration 4: For $j=5$.

$L_1\left(I_5\right)=\left\{9\right\}$, $L_2\left(I_5\right)=\{3,6\}$, $L_3\left(I_5\right)=\left\{0\right\}$.

$L_{vl}(1,I_5)=\{0,1,2,3,4,5,6,12\}$, $L_{vl}(2,I_5)=\{0,1,12\}$, $L_{vl}(3,I_5)=\{1,12\}$.

Therefore, $f_5=min\left\{L_{vl}(3,I_5)\right\}=1$ and $L\left(I_6\right)=L\left(I_5\right)\cup \left\{f_5\right\}=\{0,3,6,9\}\cup \left\{1\right\}=\{0,1,3,6,9\}$.

After iteration $4$ the graph becomes: (see Fig. 4).

Fig. 4 The interval graph of Fig. 3 after iteration $4$.

Iteration 5: For $j=6$.

$L_1\left(I_6\right)=\left\{1\right\}$, $L_2\left(I_6\right)=\left\{9\right\}$, $L_3\left(I_6\right)=\{3,6\}$.

$L_{vl}(1,I_6)=\{4,5,6,7,8,9,10,11,12\}$, $L_{vl}(2,I_6)=\{4,5,6,7,11,12\}$, $L_{vl}(3,I_6)=\{4,5,7,11,12\}$.

Therefore, $f_6=min\left\{L_{vl}(3,I_6)\right\}=4$ and $L\left(I_7\right)=L\left(I_6\right)\cup \left\{f_6\right\}=\{0,1,3,6,9\}\cup \left\{4\right\}=\{0,1,3,4,6,9\}$.

In this way, $f_7=7$, $f_8=10$, $f_9=0$, $f_{10}=13$, $f_{11}=3$, $f_{12}=6$ and finally, $f_{13}=1$.

The vertices and the label of the corresponding vertices are given below:

4 $L(4,3,2,1)$-labeling of interval graphs

By extending the idea of $L(3,2,1)$-labeling of interval graphs, we present an algorithm for $L(4,3,2,1)$-labeling of the interval graphs. In this section, we present some lemmas related to our work, upper bound of $L(4,3,2,1)$-labeling, Algorithm $L4321$ and time complexity of the proposed algorithm $L4321$ and finally an illustration of Algorithm $L4321$.

Theorem 4

For any interval graph $G$, the $L(4,3,2,1)$-labeling number ${\lambda }_{4,3,2,1}\left(G\right)$ is at most $10\Delta -6$, where $\Delta$ is the degree of the graph $G$.

Proof

Let $G$ be an interval graph with $n$ vertices and let $I=\{I_1,I_2,\dots ,I_n\}$, where $I_k$ is the interval corresponding to the vertex $v_k$ of the graph $G$. We label the intervals in ascending order of the subscript of the intervals.

Let $L\left(I_k\right)=\{0,1\dots ,10\Delta -6\}$, where $I_k\in I$. Then $\left|L\left(I_k\right)\right|=10\Delta -5$. If the set $L\left(I_k\right)$ is sufficient to label all the intervals corresponding to all the vertices of the graph $G$ satisfying $L(4,3,2,1)$-labeling condition, then we can say that ${\lambda }_{4,3,2,1}\left(G\right)\le 10\Delta -6$. We consider a situations in which the intervals $I_1,I_2,\dots ,I_{k-1}$, for $k=2,3\dots ,n$ are already labeled and $I_k,I_{k+1},\dots ,I_n$ are not labeled. In this case, we label the interval $I_k$ by $L(4,3,2,1)$-labeling. We know that $\left|L_1\left(I_k\right)\right|\le \Delta$. So in worst case $(10\Delta -5)-4\Delta =6\Delta -5$ labels of the set $L\left(I_k\right)$ are available to label the intervals which are at distance one from the interval $I_k$.

Also, since, $\left|L_2\left(I_k\right)\right|\le \Delta -1$ (By Lemma 1), so in worst case $(6\Delta -5)-3(\Delta -1)=3\Delta -2$ labels of the set $L\left(I_k\right)$ are available which satisfies the conditions of distance one and two of $L(4,3,2,1)$-labeling. Again, since, $\left|L_3\left(I_k\right)\right|\le \Delta -1$ (By Lemma 1), so in extreme unfavourable cases $(3\Delta -2)-2(\Delta -1)=\Delta$ labels of the set $L\left(I_k\right)$ are available which satisfies the conditions of distance one, two and three of $L(4,3,2,1)$-labeling. Again, since, $\left|L_4\left(I_k\right)\right|\le \Delta -1$ (By Lemma 1), so in the extreme unfavourable cases at least one (viz. $\Delta -(\Delta -1)=1$) label of the set $L\left(I_k\right)$ is available which satisfies $L(4,3,2,1)$-labeling condition. Since $I_k$ is arbitrary, so we can label any interval of the interval graph $G$ satisfying $L(4,3,2,1)$-labeling condition by using only the label of the set $L\left(I_k\right)$.

Thus, using the labels of the set $\{0,1\dots ,10\Delta -6\}$ one can $L(4,3,2,1)$-label the interval graph $G$. Therefore, ${\lambda }_{4,3,2,1}\left(G\right)\le 10\Delta -6$.  □

4.1 Algorithm for $L(4,3,2,1)$-labeling

In this subsection, an algorithm to compute the set $L_{vl}^{\prime }(k,I_j)$ for $j=2,3,\dots ,n$ and $k=1,2,3$ is designed and also we design an algorithm to $L(4,3,2,1)$-label an interval graph. We consider a situation in which some intervals (the intervals $I_k$’s with index $k<j$) are labeled by $L(4,3,2,1)$-labeling and some intervals (the intervals $I_k$’s with index $k\ge j$) are not labeled.

Lemma 5

Algorithm $L^{\prime }KVL$, $k=1,2,3,4$ correctly compute $L_{vl}^{\prime }(k,I_j)$ for $j=2,3,\dots ,n$ and the running time for this algorithm is $O\left({\Delta }^2\right)$.

Proof

According to this algorithm every element $i\in L_{vl}^{\prime }(1,I_j)$ is differ from $l_p$ by at least $4$ for each $l_p\in L_1\left(I_j\right)$. So, $|i-l_p|\ge 4$ for all $i\in L_{1vl}^{\prime }\left(I_j\right)$ and for all $l_p\in L_1\left(I_k\right)$. So the algorithm correctly computes $L_{vl}^{\prime }(1,I_j)$.

Again, according to the above algorithm for each $k=1,2,3$ every element $l_m$ of $L_{vl}^{\prime }(k+1,I_j)$ is differ from $p_n$ by at least $4-k$ for each $p_n\in L_{(k+1)}\left(I_j\right)$. So, $|l_m-p_n|\ge 4-k$ for all $l_m\in L_{vl}^{\prime }(k+1,I_j)$ and for all $p_n\in L_{k+1}^{\prime }\left(I_j\right)$, for $k=1,2,3$. Hence the algorithm correctly compute $L_{vl}^{\prime }(k,I_j)$ for $k=1,2,3$.

Since $L$ is the label set and $\left|L\right|$ be its cardinality, clearly $\left|L_i\left(I_j\right)\right|\le \left|L\right|$ for $i=1,2,3,4$ and for any $I_j\in I$ and also $r\le 10\Delta -2$, since $r=max\left\{L\left(I_j\right)\right\}+4$. So we can compute $L_{1vl}^{\prime }\left(I_j\right)$ using at most $\left|L\right|(10\Delta -2)$ times, i.e. using $O\left(\Delta \left|L\right|\right)$ times. Also, $\left|L_{vl}^{\prime }(k,I_j)\right|\le 10\Delta -5$, for $k=1,2,3$. So for each $k=1,2,3,L_{vl}^{\prime }(k+1,I_j)$ can be computed using at most $\left|L\right|(10\Delta -5)$ times, i.e. using $O\left(\Delta \left|L\right|\right)$ times. So the time complexity of the algorithm $L^{\prime }KVL$ is $O\left(\Delta \left|L\right|\right)$, i.e. $O\left({\Delta }^2\right)$, since $\left|L\right|\le 10\Delta -5$. □

Lemma 6

For any interval graph $G$ and for any $I_j\in I$, $L_{vl}^{\prime }(k,I_j)$ is the largest non empty set satisfying the condition of distance $1,2,\dots ,k$ for $k=1,2,3,4$ of $L(4,3,2,1)$-labeling, where $l\le u$ for all $l\in L_{vl}^{\prime }(k,I_j)$ and $u=max\left\{L\left(I_j\right)\right\}+4$, for any $I_j\in I$ and $k=1,2,3,4$.

Proof

Since, $u=max\left\{L\left(I_j\right)\right\}+4$ and $L_i\left(I_j\right)\subseteq L\left(I_j\right)$ for $i=1,2,3,4$ (By Lemma 2), so $|u-l_i|\ge 4$ for any $l_i\in L_i\left(I_j\right),i=1,2,3,4$. Therefore, $u\in L_{vl}^{\prime }(k,I_j)$ for $k=1,2,3,4$. Hence, for any $k=1,2,3,4$, $L_{vl}^{\prime }(k,I_j)$ is non empty. Again, let $A$ be any set of labels satisfying the condition of distance $1,2,\dots ,k$ for $k=1,2,3,4$ of $L(4,3,2,1)$-labeling, where $l\le u$ for all $l\in A$. Also, let $a\in A$. Then $|a-l_i|\ge 5-i$ for any $l_i\in L_i\left(I_j\right)$ and for $i=k-3,k-2,k-1,k$, where $i>0$. Thus, $a\in L_{vl}^{\prime }(k,I_j)$, for $k=1,2,3,4$. Therefore, $a\in A$ implies $a\in L_{vl}^{\prime }(k,I_j)$, for $k=1,2,3,4$. So, $A\subseteq L_{vl}^{\prime }(k,I_j)$, for $k=1,2,3,4$. Since $A$ is arbitrary, so for any $k=1,2,3,4$, $L_{vl}^{\prime }(k,I_j)$ is the largest non empty set of labels satisfying the condition of distance $1,2,\dots ,k$ for $k=1,2,3,4$ of $L(4,3,2,1)$-labeling, where $l\le u$ and for all $l\in L_{vl}^{\prime }(k,I_j)$. □

Theorem 5

Algorithm $L4321$ correctly labels an interval graph satisfying $L(4,3,2,1)$-labeling condition.

Proof

Let $G$ be an interval graph with $n$ vertices. And let the set of intervals of the interval graph be $I=\{I_1,I_2,\dots ,I_n\}$, also let $f_1=0$, $L\left(I_2\right)=\left\{0\right\}$. If $n=1$, then $L\left(I_2\right)$ is sufficient to label the whole graph and obviously, ${\lambda }_{4,3,2,1}\left(G\right)=0$. If $n>1$, then $L\left(I_2\right)$ is not sufficient to label the graph $G$ by $L(4,3,2,1)$-labeling, because in this case more than one label is required and $L\left(I_2\right)$ contains only one label.

We consider a situation in which the intervals $I_1,I_2,\dots ,I_{j-1}$ are already labeled for $j=2,3,\dots ,n$. In this case, we label the interval $I_j$ by $L(4,3,2,1)$-labeling. We know that $L_{vl}^{\prime }(k,I_j)$ is the largest non-empty set satisfying the condition of distance $1,2,\dots ,k$ for $k=1,2,3,4$ of $L(4,3,2,1)$-labeling, where $l\le u$ for all $l\in L_{vl}^{\prime }(k,I_j)$ and $u=max\left\{L\left(I_j\right)\right\}+4$ for any $I_j\in I$ and $k=1,2,3,4$ (By Lemma $6$). Again no label $l\le u$ and $l\notin L_{vl}^{\prime }(4,I_j)$ satisfying $L(4,3,2,1)$-labeling condition. So the labels on the set $L_{vl}^{\prime }(4,I_j)$ is the only valid label for $I_j$, which is less than or equal to $u$ and satisfies $L(4,3,2,1)$-labeling condition. Since we want to label the interval $I_j$ by $L(4,3,2,1)$-labeling, so, $f_j=q$, where $q=min\left\{L_{vl}^{\prime }(4,I_j)\right\}$. Then $q$ is the least label for $I_j$, because no label less than $q$ satisfies $L(4,3,2,1)$-labeling condition. Since, $I_j$ is arbitrary so by Algorithm $L4321$ the graph $G$ can be labeled using minimum number of labels satisfying $L(4,3,2,1)$-labeling condition and ${\lambda }_{4,3,2,1}\left(G\right)=max\{L\left(I_n\right)\bigcup \left\{f_n\right\}\}$. □

Theorem 6

The time complexity of Algorithm $L4321$ is $O\left(n{\Delta }^2\right)$, where $n$ is the number of vertices of the graph and $\Delta$ is the degree of the graph.

Proof

In Algorithm $L4321$, our aim is to find the least possible label for each interval $I_j$. By our proposed algorithm it is clear that $f_j$ can be computed if $L_{vl}^{\prime }(4,I_j)$ is computed. Now by Lemma $5$, $L^{\prime }KVL$ for $k=1,2,3,4$ takes $O\left({\Delta }^2\right)$ time to compute $L_{vl}^{\prime }(4,I_j)$. Since we need to find $L_{vl}^{\prime }(4,I_j)$ for $j=2,3,\dots ,n$, so the overall time complexity of Algorithm $L4321$ is $O\left((n-1){\Delta }^2\right)$, i.e. $O\left(n{\Delta }^2\right)$. □

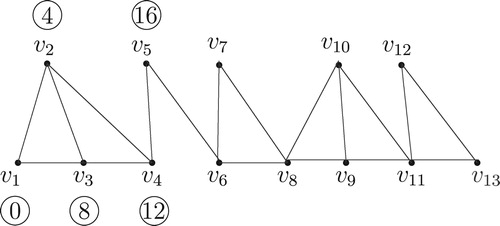
Illustration of Algorithm$L4321$

We consider an interval graph with $13$ vertices (see Fig. 5) and label this graph by Algorithm $L4321$.

Fig. 5 An interval graph labeled by $L(4,3,2,1)$-labeling. The number within the circle represents the label of the corresponding vertices.

For this graph, $V=\{v_1,v_2,\dots ,v_{13}\}$ and $\Delta =4$.

$f_j$, the label of the vertex $v_j$, for $j=1,2,\dots ,13$.

$f_1=0$, $L\left(v_2\right)=\left\{0\right\}$.

Iteration 1: For $j=2$.

$L_1\left(v_2\right)=\left\{0\right\}$, $L_2\left(v_2\right)=\varphi$, $L_3\left(v_2\right)=\varphi$, $L_4\left(v_2\right)=\varphi$.

$L_{vl}^{\prime }(1,v_2)=\left\{4\right\}$, $L_{vl}^{\prime }(2,v_2)=\left\{4\right\}$, $L_{vl}^{\prime }(3,v_2)=\left\{4\right\}$, $L_{vl}^{\prime }(4,v_2)=\left\{4\right\}$.

Therefore, $f_2=min\left\{L_{vl}^{\prime }(4,v_2)\right\}=4$ and $L\left(v_3\right)=L\left(v_2\right)\cup \left\{f_2\right\}=\left\{0\right\}\cup \left\{4\right\}=\{0,4\}$.

Iteration 2: For $j=3$.

$L_1\left(v_3\right)=\{0,4\}$, $L_2\left(v_3\right)=\varphi$, $L_3\left(v_3\right)=\varphi$, $L_4\left(v_3\right)=\varphi$.

$L_{vl}^{\prime }(1,v_3)=\left\{8\right\}$, $L_{vl}^{\prime }(2,v_3)=\left\{8\right\}$, $L_{vl}^{\prime }(3,v_3)=\left\{8\right\}$, $L_{vl}^{\prime }(4,v_3)=\left\{8\right\}$.

Therefore, $f_3=min\left\{L_{vl}^{\prime }(4,v_3)\right\}=8$ and $L\left(v_4\right)=L_0\left(v_3\right)\cup \left\{f_3\right\}=\{0,4\}\cup \left\{8\right\}=\{0,4,8\}$.

Iteration 3: For $j=4$.

$L_1\left(v_4\right)=\{0,8\}$, $L_2\left(v_4\right)=\left\{0\right\}$, $L_3\left(v_4\right)=\varphi$, $L_4\left(v_4\right)=\varphi$.

$L_{vl}^{\prime }(1,v_4)=\{0,12\}$, $L_{vl}^{\prime }(2,v_4)=\left\{12\right\}$, $L_{vl}^{\prime }(3,v_4)=\left\{12\right\}$, $L_{vl}^{\prime }(4,v_4)=\left\{12\right\}$.

Therefore, $f_4=min\left\{L_{vl}^{\prime }(4,v_4)\right\}=12$ and $L\left(v_5\right)=L\left(v_4\right)\cup \left\{f_4\right\}=\{0,4,8\}\cup \left\{12\right\}=\{0,4,8,12\}$.

Iteration 4: For $j=5$.

$L_1\left(v_5\right)=\left\{12\right\}$, $L_2\left(v_5\right)=\{4,8\}$, $L_3\left(v_5\right)=\left\{0\right\}$, $L_4\left(v_5\right)=\varphi$.

$L_{vl}^{\prime }(1,v_5)=\{0,1,2,3,5,6,7,8,16\}$, $L_{vl}^{\prime }(2,v_5)=\{0,1,16\}$, $L_{vl}^{\prime }(3,v_5)=\left\{16\right\}$, $L_{vl}^{\prime }(4,v_5)=\left\{16\right\}$.

Therefore, $f_5=min\left\{L_{vl}^{\prime }(4,v_5)\right\}=16$ and $L\left(v_6\right)=L\left(v_5\right)\cup \left\{f_5\right\}=\{0,4,8,12\}\cup \left\{16\right\}=\{0,4,8,12,16\}$.

After iteration $4$ the graph becomes: (see Fig. 6).

Fig. 6 The interval graph of Fig. 5 after iteration $4$.

Iteration 5: For $j=6$.

$L_1\left(v_6\right)=\left\{16\right\}$, $L_2\left(v_6\right)=\left\{12\right\}$, $L_3\left(v_6\right)=\{4,8\}$, $L_4\left(v_6\right)=\left\{0\right\}$.

$L_{vl}^{\prime }(1,v_6)=\{0,1,2,3,5,6,7,8,9,10,11,12,20\}$, $L_{vl}^{\prime }(2,v_6)=\{0,1,2,3,4,5,6,7,8,9,20\}$, $L_{vl}^{\prime }(3,v_5)=\{0,1,2,6,20\}$, $L_{vl}^{\prime }(4,v_5)=\{1,2,6,20\}$.

Therefore, $f_6=min\left\{L_{vl}^{\prime }(4,v_6)\right\}=1$ and $L\left(v_7\right)=L\left(v_6\right)\cup \left\{f_6\right\}=\{0,4,8,12,16\}\cup \left\{1\right\}=\{0,1,4,8,12,16\}$.

In this way, $f_7=5$, $f_8=9$, $f_9=13$, $f_{10}=18$, $f_{11}=3$, $f_{12}=7$ and finally, $f_{13}=11$.

The vertices and the label of the corresponding vertices are shown below:

5 Conclusion

In this paper, we determine the upper bounds for ${\lambda }_{3,2,1}$ and ${\lambda }_{4,3,2,1}$ for an interval graph $G$, and have shown that ${\lambda }_{3,2,1}\left(G\right)\le 6\Delta -3$ and ${\lambda }_{4,3,2,1}\left(G\right)\le 10\Delta -6$. These bounds are tighter than the previous available result [7]. Also, two algorithms are designed to $L(3,2,1)$-label and $L(4,3,2,1)$-label for interval graphs. The running time for both the algorithms are $O\left(n{\Delta }^2\right)$. We feel that the computation of exact value of ${\lambda }_{3,2,1}$ and ${\lambda }_{4,3,2,1}$ for an interval graph is very difficult. Since the result is not exact, so there is a chance for new upper bounds for the problems. Also the time complexities of the proposed algorithms may be reduced.

Notes

Peer review under responsibility of Kalasalingam University.