The adjacency spectrum of two new operations of graphs

Peer review under responsibility of Kalasalingam University.

This paper supported by the National Natural Science Foundation of China (No. 11571101) and the program for excellent talents in Hunan Normal University (ET13101).

Abstract

Let $G$ be a graph and $A=A\left(G\right)$ be its adjacency matrix. The eigenvalues ${\mu }_1,{\mu }_2,\dots ,{\mu }_n$ of $A\left(G\right)$ are the eigenvalues of $G$ and form the adjacency spectrum, denoted by $Spec\left(G\right)$. In this paper, we introduce two new operations $G_1{■}_k(G_3\square G_2)$ and $(G_4\square G_1){■}_k(G_3\square G_2)$, and describe the adjacency spectra of $G_1{■}_k(G_3\square G_2)$ and $(G_4\square G_1){■}_k(G_3\square G_2)$ of regular graphs $G_1$, $G_2$ and arbitrarily graphs $G_3$, $G_4$ in terms of their adjacency spectra. As the applications, we obtain some new integral spectrum graphs.

Keywords:

• Adjacency spectrum
• Cartesian product(of graphs)
• Integral graphs

1 Introduction

All graphs considered in this paper are undirected, finite and simple graphs. Let $G$ be a graph with the vertex set $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$. The adjacency matrix $A\left(G\right)$ of $G$ is an $n\times n$ matrix whose $(i,j)$th entry, $a_{i,j}$, is $1$ if the $i$th vertex of $G$ is adjacent to the $j$th vertex of $G$ and $0$ otherwise. The eigenvalues of $A\left(G\right)$ are called the eigenvalues of $G$ and they form the adjacency spectrum of $G$, denoted by $Spec\left(G\right)$. The properties of graph spectra and its applications were inducted in [1]. In this paper, we follow [2] for graph theoretic terminology and we only consider the adjacency spectrum of $G$.

In [3], Harary and Schwenk initiated the problem of finding (describing) all graphs with integral spectrum. In general, this problem seems to be intractable. Some special results were obtained only for certain classes of graphs (see e.g. [4–11^{[4][5][6][7][8][9][10][11]}]).

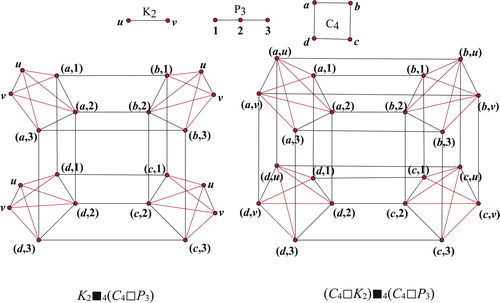
The $cartesian$ $product$ of graphs $G$ and $H$, denoted by $G\square H$, is the graph with vertex set $V\left(G\right)\times V\left(H\right)=\{(a,v):a\in V\left(G\right),v\in V\left(H\right)\}$, and $(a,v)$ is adjacent to $(b,w)$ whenever $a=b$ and $\{v,w\}\in E\left(H\right)$, or $v=w$ and $\{a,b\}\in E\left(G\right)$.

Let $G_{1i}=G_1$ and $G_{2i}=G_2$ $(1\le i\le k)$ be $k$ copies of graphs $G_1$ and $G_2$, respectively, $G_j$ $(j=3,4)$ is an arbitrary graph. The first operation $G_1{■}_k(G_3\square G_2)$ of $G_1$, $G_2$ and $G_3$ is obtained by making the Cartesian product of two graphs $G_3$ and $G_2$, thus produces $k$ copies $G_{2i}$ ($1\le i\le k$) of $G_2$, then makes $k$ joins $G_{1i}\vee G_{2i},i=1,2,\dots ,k$. Note that if $G_3=P_2$, the first operation $G_1{■}_2(P_2\square G_2)$ is the Indu–Bala product $G_1▾G_2$ in [12]. The second operation $(G_4\square G_1){■}_k(G_3\square G_2)$ of $G_1$, $G_2$, $G_3$ and $G_4$ is obtained by making the Cartesian product of two graphs $G_3$ and $G_2$, produces $k$ copies $G_{2i}$ ($1\le i\le k$) of $G_2$ and making the Cartesian product of two graphs $G_4$ and $G_1$, produces $k$ copies $G_{1i}$ ($1\le i\le k$) of $G_1$, then makes $k$ joins $G_{1i}\vee G_{2i},i=1,2,\dots ,k$. $K_2{■}_4(C_4\square P_3)$ and $(C_4\square K_2){■}_4(C_4\square P_3)$ are shown in Fig. 1.

Fig. 1 The two new operations $K_2{■}_4(C_4\square P_3)$ and $(C_4\square K_2){■}_4(C_4\square P_3)$.

In this paper, we describe the adjacency spectra of $G_1{■}_k(G_3\square G_2)$ and $(G_4\square G_1){■}_k(G_3\square G_2)$ for regular graphs $G_1$, $G_2$ and arbitrarily graphs $G_3$, $G_4$ in terms of their adjacency spectra. By using these results, we can construct new integral spectrum graphs.

2 Preliminaries

In this section, we present some lemmas which will be used later in order to prove our main results.

The Kronecker product of matrices $A=\left(a_{ij}\right)$ and $B$, denoted by $A\otimes B$, is defined to be the partition matrix $\left(a_{ij}B\right)$. See [1]. In cases where each multiplication makes sense, we have $M_1{M}_2\otimes M_3{M}_4=(M_1\otimes M_3)(M_2\otimes M_4)$.

This implies that for nonsingular matrix $M$ and $N$, ${(M\otimes N)}^{-1}=M^{-1}\otimes N^{-1}$. Recall also that for square matrices $M$ and $N$ of order $k$ and $s$, respectively. $det(M\otimes N)={\left(detM\right)}^k{\left(detN\right)}^s$.

If $M_1$ is nonsingular, then $det\left(\begin{array}{cc}\hfill M_1\hfill & \hfill M_2\hfill \\ \hfill M_3\hfill & \hfill M_4\hfill \end{array}\right)=det\left(M_1\right)det(M_4-M_3{M}_1^{-1}{M}_2).$

Let ${\mathbf{1}}_n$ be the column vector of size $n$ with all entries equal to one, ${\mathbf{0}}_n$ a column zero vector of size $n$, and $I_n$ the identity matrix of order $n$. Let $e_{1\times n}^i$ be the $i$th unit column vector of size $n$ for $i=1,2,\dots ,n$. For a vertex $u$ of a graph $G$, let $d_G\left(u\right)$ be the degree of vertex $u$ in $G$. For vertices $u$ and $v$ in a graph, $u\sim v$ means that $v$ is adjacent to $u$.

Lemma 2.1

[1]

If the graph $G_1$ has $n_1$ vertices and the $n_1\times n_1$ adjacency matrix $A_1$, and the graph $G_2$ has $n_2$ vertices and the $n_2\times n_2$ adjacency matrix $A_2$, then the adjacency matrix of the Cartesian product of both graphs is given by $A_1\square A_2=A_1\otimes I_{n_2}+I_{n_1}\otimes A_2$.

Lemma 2.2

[1]

Let $A$ and $B$ be square matrices of orders $m$ and $n$, respectively, with eigenvalues ${\lambda }_i$ $(1\le i\le m)$ and ${\mu }_j$ $(1\le i\le n)$. Then the eigenvalues of $A\otimes I_n+I_m\otimes B$ are ${\lambda }_i+{\mu }_j$. Moreover, if $X_i$ is an eigenvector of $A$ affording ${\lambda }_i$ and $Y_j$ is an eigenvector of $B$ affording ${\mu }_j$, then $X_i\otimes Y_j$ is an eigenvector of $A\otimes I_n+I_m\otimes B$ affording ${\lambda }_i+{\mu }_j$.

3 The adjacency spectra of $G_1{■}_k(G_3\square G_2)$ and $(G_4\square G_1){■}_k(G_3\square G_2)$

First we will describe the spectrum of $G_1{■}_k(G_3\square G_2)$ for regular graphs $G_1$, $G_2$ and an arbitrary graph $G_3$ in terms of their spectra.

Theorem 3.1

For $i=1,2$, let $G_i$ be an $r_i$ regular graph with $n_i$ vertices and ${\lambda }_{i,1}=r_i\ge {\lambda }_{i,2}\ge {\lambda }_{i,3}\ge \cdots \cdot \cdot \ge {\lambda }_{i,n_i}$ be the eigenvalues of $G_i$. Let $G_3$ be an arbitrary graph with $\left|V\left(G_3\right)\right|=k$, $V\left(G_3\right)=\{v_1,v_2,\dots ,v_k\}$ and $Spec\left(G_3\right)=\{{\mu }_{3,1},{\mu }_{3,2},\dots ,{\mu }_{3,k}\}$. Then the spectrum of $G_1{■}_k(G_3\square G_2)$ is the multi-set consisting of the numbers ${\lambda }_{1,j}$ for $j=2,3,\dots ,n_1$, each with multiplicity $k$; ${\mu }_{3,j}+{\lambda }_{2,i}$ for $i=2,\dots ,n_2,j=1,2,\dots ,k$; $2k$ multiplicity-one eigenvalues $\frac{(r_1+r_2+{\mu }_{3,j})\pm \sqrt{{(r_1-r_2-{\mu }_{3,j})}^2+4n_1{n}_2}}{2}$ for each eigenvalue ${\mu }_{3,j}$ $(j=1,2,\dots ,k)$ of $A\left(G_3\right)$.

Proof

By a proper labeling of the vertices and Lemma 2.1, the adjacency matrix $A$ of $G_1{■}_k(G_3\square G_2)$ can be written in the following form ($J$ stands for the all-$1$ matrix): $A=\left[\begin{array}{cc}\hfill I_k\otimes A_1\hfill & \hfill I_k\otimes J_{n_1\times n_2}\hfill \\ \hfill I_k\otimes J_{n_2\times n_1}\hfill & \hfill A_3\otimes I_{n_2}+I_k\otimes A_2\hfill \end{array}\right],$where $A_i=A\left(G_i\right)$ $(i=1,2,3)$.

As a regular graph, $G_1$ has the all-one vector $\mathbf{1}$ as an eigenvector corresponding to the eigenvalue $r_1$, while all the other eigenvectors are orthogonal to $\mathbf{1}$. Note that as $G_1$ may not be connected, $r_1$ need not be a simple eigenvalue of $G_1$. Let ${\lambda }_{1,j}$ $(j=2,\dots ,n_1)$ be an arbitrary eigenvalue of $A\left(G_1\right)$ with corresponding eigenvector $X_j$, such that ${\mathbf{1}}^T{X}_j=0$. For each $p=1,2,\dots ,k$, ${[e_{1\times k}^p\otimes X_j,{\mathbf{0}}_{1\times k{n}_2}]}^T$ is an eigenvector of $A$ corresponding to the eigenvalue ${\lambda }_{1,j}$. This is because $\left[\begin{array}{cc}\hfill I_k\otimes A_1\hfill & \hfill I_k\otimes J_{n_1\times n_2}\hfill \\ \hfill I_k\otimes J_{n_2\times n_1}\hfill & \hfill A_3\otimes I_{n_2}+I_k\otimes A_2\hfill \end{array}\right]\left[\begin{array}{c}\hfill e_{k\times 1}^p\otimes X_j\hfill \\ \hfill {\mathbf{0}}_{k{n}_2\times 1}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \left(I_k{e}_{k\times 1}^p\right)\otimes \left(A_1{X}_j\right)\hfill \\ \hfill \left(I_k{e}_{k\times 1}^p\right)\otimes \left(J_{n_2\times n_1}{X}_j\right)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill e_{k\times 1}^p\otimes \left({\lambda }_{1,j}{X}_j\right)\hfill \\ \hfill {\mathbf{0}}_{k{n}_2\times 1}\hfill \end{array}\right]={\lambda }_{1,j}\left[\begin{array}{c}\hfill e_{n_1\times 1}^p\otimes X_j\hfill \\ \hfill {\mathbf{0}}_{k{n}_2\times 1}\hfill \end{array}\right].$

Let ${\lambda }_{2,i}$ $(i=2,\dots ,n_2)$ be an arbitrary eigenvalue of $A\left(G_2\right)$ with corresponding eigenvector $Y_i$, such that $1^T{Y}_i=0$. Let ${\mu }_{3,j}$ $(j=1,2,\dots ,k)$ be an arbitrary eigenvalue of $A\left(G_3\right)$ with corresponding eigenvector $Z_j$. By Lemma 2.2 and a similar argument we see that the $k(n_2-1)$ vectors ${[{\mathbf{0}}_{1\times k{n}_1},Z_j\otimes Y_i]}^T$ are eigenvectors of $A$ with corresponding eigenvalues ${\mu }_{3,j}+{\lambda }_{2,i}$.

In this way we obtain eigenvectors of the form ${[e_{1\times k}^p\otimes X_j,{\mathbf{0}}_{1\times k{n}_2}]}^T$, ${[{\mathbf{0}}_{1\times k{n}_1},Z_j\otimes Y_i]}^T$ and these account for a total of $k(n_1-1)+k(n_2-1)$ eigenvectors. All these eigenvectors are orthogonal to the $2k$ vectors ${[{\mathbf{0}}_{1\times (t-1)n_1},{\mathbf{1}}_{1\times n_1},{\mathbf{0}}_{1\times (k{n}_1-t{n}_1+k{n}_2)}]}^T$ and $[{\mathbf{0}}_{1\times (k{n}_1+(t-1)n_2)},{\mathbf{1}}_{1\times n_2},{\mathbf{0}}_{1\times (k-t)n_2}]{}^T,1\le t\le k$. This means that these $2k$ vectors span the space spanned by the remaining $2k$ eigenvectors of $A$. Thus the remaining $2k$ eigenvectors of $A$ are of the form ${[a_1{\mathbf{1}}_{1\times n_1},a_2{\mathbf{1}}_{1\times n_1},\dots ,a_k{\mathbf{1}}_{1\times n_1},b_1{\mathbf{1}}_{1\times n_2},b_2{\mathbf{1}}_{1\times n_2},\dots ,b_k{\mathbf{1}}_{1\times n_2}]}^T={[a^{\prime }\otimes {\mathbf{1}}_{1\times n_1},b^{\prime }\otimes {\mathbf{1}}_{1\times n_2}]}^T$ for some $[a_1,a_2,\dots ,a_k,b_1,b_2,\dots ,b_k]\ne {\mathbf{0}}_{1\times 2k}$, where $a^{\prime }=[a_1,a_2,\dots ,a_k]$ and $b^{\prime }=[b_1,b_2,\dots ,b_k]$.

If $\nu$ is an eigenvalue of $A$ with an eigenvector ${[a^{\prime }\otimes {\mathbf{1}}_{1\times n_1},b^{\prime }\otimes {\mathbf{1}}_{1\times n_2}]}^T$, then $A{[a^{\prime }\otimes {\mathbf{1}}_{1\times n_1},b^{\prime }\otimes {\mathbf{1}}_{1\times n_2}]}^T=\nu {[a^{\prime }\otimes {\mathbf{1}}_{1\times n_1},b^{\prime }\otimes {\mathbf{1}}_{1\times n_2}]}^T$and $A_{G_1}{\mathbf{1}}_{1\times n_1}^T=r_1{\mathbf{1}}_{1\times n_1}^T$, $A_{G_2}{\mathbf{1}}_{1\times n_2}^T=r_2{\mathbf{1}}_{1\times n_2}^T$. We get the system of $2k$ equations: (1) $\left\{\begin{array}{cc}\hfill a_i{r}_1+b_i{n}_2=\nu a_i,& \hfill i=1,2,\dots ,k;\hfill \\ \hfill a_i{n}_1+b_i{r}_2+\sum _{v_i\sim v_j}{b}_j=\nu b_i,& \hfill i=1,2,\dots ,k;\hfill \end{array}\right.$(1) where $v_i,v_j\in V\left(G_3\right)$.

This shows that $\nu$ is also an eigenvalue of the matrix $M_1$ since $[a_1,a_2,\dots ,a_k,b_1,b_2,\dots ,b_k]\ne {\mathbf{0}}_{1\times 2k}$, where $M_1=\left[\begin{array}{cc}\hfill r_1{I}_k\hfill & \hfill n_2{I}_k\hfill \\ \hfill n_1{I}_k\hfill & \hfill r_2{I}_k+A_{G_3}\hfill \end{array}\right].$

Next we consider the eigenvalues of the matrix $M_1$, equivalently consider the roots of $det(\nu I_{2k}-M_1)=0$, and if $\nu =r_1$, (1(1) $\left\{\begin{array}{cc}\hfill a_i{r}_1+b_i{n}_2=\nu a_i,& \hfill i=1,2,\dots ,k;\hfill \\ \hfill a_i{n}_1+b_i{r}_2+\sum _{v_i\sim v_j}{b}_j=\nu b_i,& \hfill i=1,2,\dots ,k;\hfill \end{array}\right.$(1) ) gives $b_i=0$, since $b_i{n}_2=0$, $n_2>0$ and this in turn implies $a_i=0$, since $n_1>0$, a contradiction. Thus $\nu \ne r_1$, so $(\nu -r_1)I_k$ is nonsingular, we have $det(\nu I_{2k}-M_1)=det\left((\nu -r_1)I_k\right)det((\nu -r_2)I_k-A_{G_3}-\left(n_2{(\nu -r_1)}^{-1}{n}_1\right)I_k)={(\nu -r_1)}^{k}det((\nu -r_2-\frac{n_1{n}_2}{\nu -r_1})I_k-A_{G_3}).$Thus, the $2k$ eigenvalues are obtained by solving $\nu -r_2-\frac{n_1{n}_2}{\nu -r_1}={\mu }_{3,j}$ $(j=1,2,\dots ,k)$ because of $Spec\left(G_3\right)=\{{\mu }_{3,1},{\mu }_{3,2},\dots ,{\mu }_{3,k}\}$, thus eigenvalues are $\nu =\frac{(r_1+r_2+{\mu }_{3,j})\pm \sqrt{{(r_1-r_2-{\mu }_{3,j})}^2+4n_1{n}_2}}{2}$the theorem is proved.

If we allow $G_3=P_2$, the spectrum of $G_1{■}_2(P_2\square G_2)$ is the spectrum of the Indu–Bala product $G_1▾G_2$. Then we have the following.

Corollary 3.2

For $i=1,2$, let $G_i$ be an $r_i$ regular graph with $n_i$ vertices and ${\lambda }_{i,1}=r_i\ge {\lambda }_{i,2}\ge {\lambda }_{i,3}\ge \cdots \cdot \cdot \ge {\lambda }_{i,n_i}$ be the eigenvalues of $G_i$. Let $G_3$ be $P_2$ and $Spec\left(P_2\right)=\{1,-1\}$. Then the spectrum of $G_1{■}_2(P_2\square G_2)$ is the multi-set consisting of the numbers ${\lambda }_{1,j}$ for $j=2,3,\dots ,n_1$, each with multiplicity $2$; $\pm 1+{\lambda }_{2,i}$ for $i=2,\dots ,n_2$ and four more eigenvalues are $\frac{(r_1+r_2+1)\pm \sqrt{{(r_1-r_2-1)}^2+4n_1{n}_2}}{2}$ and $\frac{(r_1+r_2-1)\pm \sqrt{{(r_1-r_2+1)}^2+4n_1{n}_2}}{2}$.

Proof

By Theorem 3.1, the spectrum of $G_1{■}_2(P_2\square G_2)$ is the multi-set consisting of the numbers ${\lambda }_{1,j}$ for $j=2,3,\dots ,n_1$, each with multiplicity $2$; $\pm 1+{\lambda }_{2,i}$ for $i=2,\dots ,n_2$ and $4$ more eigenvalues are $\frac{(r_1+r_2+1)\pm \sqrt{{(r_1-r_2-1)}^2+4n_1{n}_2}}{2}$ and $\frac{(r_1+r_2-1)\pm \sqrt{{(r_1-r_2+1)}^2+4n_1{n}_2}}{2}$, because of ${\mu }_{3,j}=\pm 1$, the theorem is proved.

In the following, we will consider the spectrum of $(G_4\square G_1){■}_k(G_3\square G_2)$ for regular graphs $G_1$, $G_2$ and arbitrary graphs $G_3$, $G_4$ in terms of their spectra.

Theorem 3.3

For $i=1,2$, let $G_i$ be an $r_i$ regular graph with $n_i$ vertices and let ${\lambda }_{i,1}=r_i\ge {\lambda }_{i,2}\ge {\lambda }_{i,3}\ge \cdots \cdot \cdot \ge {\lambda }_{i,n_i}$ be the eigenvalues of $G_i$. Let $G_j$ $(j=3,4)$ be an arbitrary graph with $\left|V\left(G_j\right)\right|=k$, $V\left(G_3\right)=\{v_1,v_2,\dots ,v_k\}$, $V\left(G_4\right)=\{u_1,u_2,\dots ,u_k\}$ and $Spec\left(G_j\right)=\{{\mu }_{j,1},{\mu }_{j,2},\dots ,{\mu }_{j,k}\}$. Then the spectrum of $(G_4\square G_1){■}_k(G_3\square G_2)$ is the multi-set consisting of the numbers ${\mu }_{4,j}+{\lambda }_{1,i}$ for $i=2,3,\dots ,n_1,j=1,2,\dots ,k$; ${\mu }_{3,j}+{\lambda }_{2,i}$ for $i=2,\dots ,n_2,j=1,2,\dots ,k$; and $2k$ eigenvalues of a $2k\times 2k$ real matrix $M_2$, where $M_2=\left[\begin{array}{cc}\hfill r_1{I}_k+A_{G_4}\hfill & \hfill n_2{I}_k\hfill \\ \hfill n_1{I}_k\hfill & \hfill r_2{I}_k+A_{G_3}\hfill \end{array}\right].$

Proof

By a proper labeling of the vertices and Lemma 2.1, the adjacency matrix $A$ of $(G_4\square G_1){■}_k(G_3\square G_2)$ can be written in the form: $A=\left[\begin{array}{cc}\hfill A_4\otimes I_{n_1}+I_k\otimes A_1\hfill & \hfill I_k\otimes J_{n_1\times n_2}\hfill \\ \hfill I_k\otimes J_{n_2\times n_1}\hfill & \hfill A_3\otimes I_{n_2}+I_k\otimes A_2\hfill \end{array}\right],$where $A_i=A\left(G_i\right)$ $(i=1,2,3,4)$.

Let ${\lambda }_{1,i}$ $(i=2,3,\dots ,n_1)$ be an arbitrary eigenvalue of $A\left(G_1\right)$ with corresponding eigenvector $X_i$, such that ${\mathbf{1}}^T{X}_i=0$. Let ${\mu }_{4,j}$ be an arbitrary eigenvalue of $A\left(G_4\right)$ with corresponding eigenvector $W_j$. For each $i=2,3,\dots ,n_1$ and $j=1,2,\dots ,k$, the $k(n_1-1)$ vectors ${[W_j\otimes X_i,{\mathbf{0}}_{1\times k{n}_2}]}^T$ are eigenvectors of $A$ corresponding to the eigenvalue ${\mu }_{4,j}+{\lambda }_{1,i}$. This is because $\left[\begin{array}{cc}\hfill A_4\otimes I_{n_1}+I_k\otimes A_1\hfill & \hfill I_k\otimes J_{n_1\times n_2}\hfill \\ \hfill I_k\otimes J_{n_2\times n_1}\hfill & \hfill A_3\otimes I_{n_2}+I_k\otimes A_2\hfill \end{array}\right]\left[\begin{array}{c}\hfill W_j\otimes X_i\hfill \\ \hfill {\mathbf{0}}_{k{n}_2\times 1}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \left(A_4{W}_j\right)\otimes \left(I_{n_1}{X}_i\right)+\left(I_k{W}_j\right)\otimes \left(A_1{X}_i\right)\hfill \\ \hfill {\mathbf{0}}_{k{n}_2\times 1}\hfill \end{array}\right]=({\mu }_{4,j}+{\lambda }_{1,i})\left[\begin{array}{c}\hfill W_j\otimes X_i\hfill \\ \hfill {\mathbf{0}}_{k{n}_2\times 1}\hfill \end{array}\right].$

Similarly, let ${\lambda }_{2,i}$ $(i=2,3,\dots ,n_2)$ be an arbitrary eigenvalue of $A\left(G_2\right)$ with corresponding eigenvector $Y_i$, such that $1^T{Y}_i=0$. Let ${\mu }_{3,j}$ $(j=1,2,\dots ,k)$ be an arbitrary eigenvalue of $A\left(G_3\right)$ with corresponding eigenvector $Z_j$. By Lemma 2.2 and a similar argument we see that the $k(n_2-1)$ vectors ${[{\mathbf{0}}_{1\times k{n}_1},Z_j\otimes Y_i]}^T$ are eigenvectors of $A$ with corresponding eigenvalues ${\mu }_{3,j}+{\lambda }_{2,i}$.

In this way we obtain eigenvectors of the form ${[W_j\otimes X_i,{\mathbf{0}}_{1\times k{n}_2}]}^T$, ${[{\mathbf{0}}_{1\times k{n}_1},Z_j\otimes Y_i]}^T$ and these account for a total of $k(n_1-1)+k(n_2-1)$ eigenvectors. All these eigenvectors are orthogonal to the $2k$ vectors ${[{\mathbf{0}}_{1\times (t-1)n_1},{\mathbf{1}}_{1\times n_1},{\mathbf{0}}_{1\times (k{n}_1-t{n}_1+k{n}_2)}]}^T$ and $[{\mathbf{0}}_{1\times (k{n}_1+(t-1)n_2)},{\mathbf{1}}_{1\times n_2},{\mathbf{0}}_{1\times (k-t)n_2}]{}^T,1\le t\le k$. This means that these $2k$ vectors span the space spanned by the remaining $2k$ eigenvectors of $A$. Thus the remaining $2k$ eigenvectors of $A$ are of the form ${[a_1{\mathbf{1}}_{1\times n_1},a_2{\mathbf{1}}_{1\times n_1},\dots ,a_k{\mathbf{1}}_{1\times n_1},b_1{\mathbf{1}}_{1\times n_2},b_2{\mathbf{1}}_{1\times n_2},\dots ,b_k{\mathbf{1}}_{1\times n_2}]}^T={[a^{\prime }\otimes {\mathbf{1}}_{1\times n_1},b^{\prime }\otimes {\mathbf{1}}_{1\times n_2}]}^T$ for some $[a_1,a_2,\dots ,a_k,b_1,b_2,\dots ,b_k]\ne {\mathbf{0}}_{1\times 2k}$, where $a^{\prime }=[a_1,a_2,\dots ,a_k]$ and $b^{\prime }=[b_1,b_2,\dots ,b_k]$.

If $\nu$ is an eigenvalue of $A$ with an eigenvector ${[a^{\prime }\otimes {\mathbf{1}}_{1\times n_1},b^{\prime }\otimes {\mathbf{1}}_{1\times n_2}]}^T$, then $A{[a^{\prime }\otimes {\mathbf{1}}_{1\times n_1},b^{\prime }\otimes {\mathbf{1}}_{1\times n_2}]}^T=\nu {[a^{\prime }\otimes {\mathbf{1}}_{1\times n_1},b^{\prime }\otimes {\mathbf{1}}_{1\times n_2}]}^T$and $A_{G_1}{\mathbf{1}}_{1\times n_1}^T=r_1{\mathbf{1}}_{1\times n_1}^T$, $A_{G_2}{\mathbf{1}}_{1\times n_2}^T=r_2{\mathbf{1}}_{1\times n_2}^T$. We get the system of $2k$ equations: (2) $\left\{\begin{array}{cc}\hfill a_i{r}_1+\sum _{u_i\sim u_j}{a}_j+b_i{n}_2=\nu a_i,& \hfill i=1,2,\dots ,k;\hfill \\ \hfill a_i{n}_1+b_i{r}_2+\sum _{v_i\sim v_j}{b}_j=\nu b_i,& \hfill i=1,2,\dots ,k;\hfill \end{array}\right.$(2) where $u_i,u_j\in V\left(G_4\right)$ and $v_i,v_j\in V\left(G_3\right)$.

This shows that $\nu$ is also an eigenvalue of the matrix $M_2$ since $[a_1,a_2,\dots ,a_k,b_1,b_2,\dots ,b_k]\ne {\mathbf{0}}_{1\times 2k}$, where $M_2=\left[\begin{array}{cc}\hfill r_1{I}_k+A_{G_4}\hfill & \hfill n_2{I}_k\hfill \\ \hfill n_1{I}_k\hfill & \hfill r_2{I}_k+A_{G_3}\hfill \end{array}\right].\square$

In general, it is difficult to give the explicit formula for all eigenvalues of $2k\times 2k$ matrix $M_2$. But for $k=2,3$, and the cases $G_j=P_2$ or $C_3$ $(j=3,4)$, we have the following.

Corollary 3.4

For $i=1,2$, let $G_i$ be an $r_i$ regular graph with $n_i$ vertices and let ${\lambda }_{i,1}=r_i\ge {\lambda }_{i,2}\ge {\lambda }_{i,3}\ge \cdots \cdot \cdot \ge {\lambda }_{i,n_i}$ be the eigenvalues of $G_i$. Let $G_3$, $G_4$ be $P_2$ and $Spec\left(P_2\right)=\{1,-1\}$. Then the spectrum of $(P_2\square G_1){■}_2(P_2\square G_2)$ is the multi-set consisting of the numbers $\pm 1+{\lambda }_{1,i}$ for $i=2,3,\dots ,n_1$; $\pm 1+{\lambda }_{2,i}$ for $i=2,\dots ,n_2$ and four eigenvalues are $\frac{(r_1+r_2-2)\pm \sqrt{{(r_1-r_2)}^2+4n_1{n}_2}}{2}$ and $\frac{(r_1+r_2+2)\pm \sqrt{{(r_1-r_2)}^2+4n_1{n}_2}}{2}$.

Proof

By Theorem 3.3, the spectrum of $(P_2\square G_1){■}_2(P_2\square G_2)$ is the multi-set consisting of the numbers $\pm 1+{\lambda }_{1,i}$ for $i=2,3,\dots ,n_1$; $\pm 1+{\lambda }_{2,i}$ for $i=2,\dots ,n_2$; and four eigenvalues which are the eigenvalues of matrix $M_2$ $M_2=\left[\begin{array}{cc}\hfill r_1{I}_2+A_{P_2}\hfill & \hfill n_2{I}_2\hfill \\ \hfill n_1{I}_2\hfill & \hfill r_2{I}_2+A_{P_2}\hfill \end{array}\right]=\left[\begin{array}{cccc}\hfill r_1\hfill & \hfill 1\hfill & \hfill n_2\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill r_1\hfill & \hfill 0\hfill & \hfill n_2\hfill \\ \hfill n_1\hfill & \hfill 0\hfill & \hfill r_2\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill n_1\hfill & \hfill 1\hfill & \hfill r_2\hfill \end{array}\right].$and the characteristic polynomial of $M_2$ is $[x^2+(2-r_1-r_2)x-n_1{n}_2-r_1-r_2+r_1{r}_2+1][x^2-(2+r_1+r_2)x-n_1{n}_2+r_1+r_2+r_1{r}_2+1]=0$, then eigenvalues are $x=\frac{(r_1+r_2-2)\pm \sqrt{{(r_1-r_2)}^2+4n_1{n}_2}}{2}$ and $x=\frac{(r_1+r_2+2)\pm \sqrt{{(r_1-r_2)}^2+4n_1{n}_2}}{2}$.

Corollary 3.5

For $i=1,2$, let $G_i$ be an $r_i$ regular graph with $n_i$ vertices and let ${\lambda }_{i,1}=r_i\ge {\lambda }_{i,2}\ge {\lambda }_{i,3}\ge \cdots \cdot \cdot \ge {\lambda }_{i,n_i}$ be the eigenvalues of $G_i$. Let $G_3$, $G_4$ be $C_3$ and $Spec\left(C_3\right)=\{2,-1,-1\}$. Then the spectrum of $(C_3\square G_1){■}_3(C_3\square G_2)$ is the multi-set consisting of the numbers $2+{\lambda }_{1,i}$ for $i=2,3,\dots ,n_1$; $-1+{\lambda }_{1,i}$ for $i=2,\dots ,n_1$, each with multiplicity $2$; $2+{\lambda }_{2,i}$ for $i=2,3,\dots ,n_2$; $-1+{\lambda }_{2,i}$ for $i=2,\dots ,n_2$ each with multiplicity $2$ and six eigenvalues are $\frac{(r_1+r_2-2)\pm \sqrt{{(r_1-r_2)}^2+4n_1{n}_2}}{2}$, each with multiplicity $2$ and $\frac{(r_1+r_2+4)\pm \sqrt{{(r_1-r_2)}^2+4n_1{n}_2}}{2}$.

Proof

By Theorem 3.3, the spectrum of $(C_3\square G_1){■}_k(C_3\square G_2)$ is the multi-set consisting of the numbers $2+{\lambda }_{1,i}$ for $i=2,3,\dots ,n_1$; $-1+{\lambda }_{1,i}$ for $i=2,\dots ,n_1$, each with multiplicity $2$; $2+{\lambda }_{2,i}$ for $i=2,3,\dots ,n_2$; $-1+{\lambda }_{2,i}$ for $i=2,\dots ,n_2$ each with multiplicity $2$ and six eigenvalues which are the eigenvalues of matrix $M_2$ $M_2=\left[\begin{array}{cccccc}\hfill r_1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill n_2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill r_1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill n_2\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill r_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill n_2\hfill \\ \hfill n_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill r_2\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill n_1\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill r_2\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill n_1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill r_2\hfill \end{array}\right].$and the characteristic polynomial of $M_2$ is ${[x^2+(2-r_1-r_2)x-n_1{n}_2-r_1-r_2+r_1{r}_2+1]}^2[x^2-(4+r_1+r_2)x-n_1{n}_2+2r_1+2r_2+r_1{r}_2+4]=0$, then eigenvalues are $x=\frac{(r_1+r_2-2)\pm \sqrt{{(r_1-r_2)}^2+4n_1{n}_2}}{2}$ and $x=\frac{(r_1+r_2+4)\pm \sqrt{{(r_1-r_2)}^2+4n_1{n}_2}}{2}$.

4 Some new integral adjacency spectrum

Which graphs have integral spectra? The number of integral graphs is not only infinite, but one can find them in all classes of graphs and among graphs of all orders. However, they are very rare and difficult to be found [11].

By Corollary 3.2 computation, we have that $\overline{K_s}{■}_2(P_2\square \overline{K_{s+1}})$ is an integral spectrum graph. In [13], Wang also shows this result.

Theorem 4.1

Let $G_i$ $(i=1,2)$ are both $r$-regular integral graphs with $n_i$ vertices such that $n_1{n}_2=4t^2$ where $t$ is also a positive integer and $G_3=K_{3t,3t}$ $(t\in N^{\ast })$. Then $G_1{■}_{6t}(K_{3t,3t}\square G_2)$ is an integral spectrum graph.

Proof

By Theorem 3.1, we mainly consider $12t$ multiplicity-one eigenvalues $x=\frac{(r_1+r_2+{\mu }_{3,j})\pm \sqrt{{(r_1-r_2-{\mu }_{3,j})}^2+4n_1{n}_2}}{2}$where ${\mu }_{3,j}$ $(j=1,2,\dots ,6t)$ is an eigenvalue of $K_{3t,3t}$. For $r_1=r_2=r$ and $n_1{n}_2=4t^2$, then $x=\frac{(2r+{\mu }_{3,j})\pm \sqrt{{\left({\mu }_{3,j}\right)}^2+16t^2}}{2}.$We know $Spec\left(K_{3t,3t}\right)=\{3t,0^{6t-2},-3t\}$, when ${\mu }_{3,j}=0$, then $x=r\pm 2t$, each with multiplicity $6t-2$; when ${\mu }_{3,j}=3t$, then $x=r+4t$ or $x=r-t$; when ${\mu }_{3,j}=-3t$, then $x=r-4t$ or $x=r+t$.

Thus, the spectrum of $G_1{■}_{6t}(K_{3t,3t}\square G_2)$ is $\left(\begin{array}{cccccccccc}\hfill {\lambda }_{1,i}\hfill & \hfill 3t+{\lambda }_{2,i}\hfill & \hfill -3t+{\lambda }_{2,i}\hfill & \hfill {\lambda }_{2,i}\hfill & \hfill r+2t\hfill & \hfill r-2t\hfill & \hfill r+4t\hfill & \hfill r-t\hfill & \hfill r-4t\hfill & \hfill r+t\hfill \\ \hfill 6t\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill (6t-2)\hfill & \hfill 6t-2\hfill & \hfill 6t-2\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right).$where ${\lambda }_{1,i}$ $(i=2,\dots ,n_1)$ and ${\lambda }_{2,i}$ $(i=2,\dots ,n_2)$ are eigenvalues of $G_1$, $G_2$.

As $G_1$, $G_2$ are both $r$-regular integral graphs, we have that $G_1{■}_{6t}(K_{3t,3t}\square G_2)$ is an integral spectrum graph.

Theorem 4.2

Let $s,t$ be a positive integer such that $st=p^2$ where p is also a positive integer, then $(P_2\square \overline{K_s}){■}_2(P_2\square \overline{K_t})$ and $(C_3\square \overline{K_s}){■}_3(C_3\square \overline{K_t})$ are both integral spectrum graphs.

Proof

By Corollaries 3.4 and 3.5, we can obtain the spectrum of $(P_2\square \overline{K_s}){■}_2(P_2\square \overline{K_t})$ is $\left(\begin{array}{cccccc}\hfill p+1\hfill & \hfill p-1\hfill & \hfill 1\hfill & \hfill -1\hfill & \hfill -p+1\hfill & \hfill -p-1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill s+t-2\hfill & \hfill s+t-2\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right).$

and the spectrum of $(C_3\square \overline{K_s}){■}_3(C_3\square \overline{K_t})$ is $\left(\begin{array}{cccccc}\hfill p+2\hfill & \hfill p-1\hfill & \hfill 2\hfill & \hfill -1\hfill & \hfill -p+2\hfill & \hfill -p-1\hfill \\ \hfill 1\hfill & \hfill 2\hfill & \hfill s+t-2\hfill & \hfill 2(s+t-2)\hfill & \hfill 1\hfill & \hfill 2\hfill \end{array}\right).$Hence, they are integral spectra.

Finally, the first new graph operation can also be used in constructing cospectral graphs. If $G_1$ and $G_1^{\prime }$, $G_2$ and $G_2^{\prime }$, $G_3$ and $G_3^{\prime }$ are cospectral, then $G_1{■}_k(G_3\square G_2)$ and $G_1^{\prime }{■}_k(G_3^{\prime }\square G_2^{\prime })$ are cospectral.

Notes

Peer review under responsibility of Kalasalingam University.

This paper supported by the National Natural Science Foundation of China (No. 11571101) and the program for excellent talents in Hunan Normal University (ET13101).