Nilpotent graphs with crosscap at most two

Peer review under responsibility of Kalasalingam University.

Abstract

Let $R$ be a commutative ring with identity. The nilpotent graph of $R$, denoted by ${\Gamma }_N\left(R\right)$, is a graph with vertex set ${\mathcal{Z}}_N{\left(R\right)}^{\ast }$, and two vertices $x$ and $y$ are adjacent if and only if $xy$ is nilpotent, where ${\mathcal{Z}}_N\left(R\right)=\{x\in R:xy\text{is nilpotent, for some}y\in R^{\ast }\}$. In this paper, we characterize finite rings (up to isomorphism) with identity whose nilpotent graphs can be embedded in the projective plane or Klein bottle. Also, we classify finite rings whose nilpotent graphs are ring graph or outerplanarity index 1,2.

Keywords:

• Crosscap
• Nilpotent
• Planar
• Outerplanar
• Projective

1 Introduction

Throughout, rings are commutative with $1\ne 0$. The zero-divisor of a ring $R$ is denoted by $Z\left(R\right)$ and $Z^{\ast }\left(R\right)=Z\left(R\right)-\left\{0\right\}$. The zero-divisor graph of $R$, denoted by $\Gamma \left(R\right)$, is an undirected graph whose vertices are elements of $Z^{\ast }\left(R\right)$ and two distinct vertices $a$ and $b$ are adjacent if and only if $ab=0$. The zero-divisor graph of a commutative ring was first investigated by Beck [1]. He was interested in coloring of the graph $\Gamma \left(R\right)$.

Later, it was modified as in present form by Anderson and Livingston [2]. This paper deals with the nilpotent graph of rings. Recall that the nilpotent graph of $R$, denoted by ${\Gamma }_N\left(R\right)$, is a graph with vertex set ${\mathcal{Z}}_N{\left(R\right)}^{\ast }$, and two vertices $x$ and $y$ are adjacent if and only if $xy$ is nilpotent, where ${\mathcal{Z}}_N\left(R\right)=\{x\in R:xy\text{is nilpotent,}\text{for some}y\in R^{\ast }\}$. It was first investigated by Chen [3]. He consoders all the elements of ring $R$ as the vertices of the graph and two vertices $x$ and $y$ are adjacent if and only if $xy$ is nilpotent. However, in 2010, Li [4] modified and studied the nilpotent graph ${\Gamma }_N\left(R\right)$ of $R$. Note that the usual zerodivisor graph $\Gamma \left(R\right)$ is a subgraph of the graph ${\Gamma }_N\left(R\right)$. If $R\cong F_1\times F_2\times \cdots \times F_n$,where each $F_i$ is a field and $n\ge 2$, then ${\Gamma }_N\left(R\right)\cong \Gamma \left(R\right)$.

The focus of this paper is on finding non-orientable genus(crosscap) of the graph ${\Gamma }_N\left(R\right)$. This work is motivated by the following result of Hsieh [5] who completely determined the finite commutative rings whose zero-divisor graphs are projective planar. This paper is organized as follows: In Section 2, we characterize finite rings (up to isomorphism) with identity whose nilpotent graphs can be embedded in the projective plane or Klein bottle. In Section 3, we classify finite rings whose nilpotent graphs are ring graph or outerplanar.

One can refer to [6] for the following: We denote the ring of integers modulo $n$ by ${\mathbb{Z}}_n$ and the field with $q$ elements by ${\mathbb{F}}_q$. If $S$ is a subset of $R$,we denote $S^{\ast }=S-\left\{0\right\},R^{\times }=U\left(R\right)=$ set of units of $R$ and Spec(R) is the set of all prime ideals of $R$. If $R$ is a direct product of local rings, then $0_R$ denotes the zero element of $R$. We use $K_n$ for the complete graph with $n$ vertices and $K_{m,n}$ for the complete bipartite graph.

One can refer to [7] for the following: By a surface, we mean a connected two-dimensional real manifold, i.e., a connected topological space such that each point has a neighborhood homeomorphic to an open disc. Every non-orientable compact surface ${\mathcal{N}}_k$ is a connected sum of finite copies of $k$ projective planes (see [7]). The number of copies of projective planes is called the crosscap number (non-orientable genus) of this surface. The crosscap of a graph $G$, denoted $\bar{\gamma }\left(G\right)$, is the smallest integer $k$ such that the graph can be embedded in ${\mathcal{N}}_k$. For example, the projective plane is of crosscap one and the Klein bottle is of crosscap two. A non-planar graph is said to be projective if it can be embedded into a projective plane. The following results are used in the subsequent section.

Lemma 1

[7]

Let $m,n$ be integers and for a real number $x$, let $⌈x⌉$ denote the smallest integer that is greater than or equal to $x$. Then

(i)	$\overline{\gamma }\left(K_n\right)=\left\{\begin{array}{cc}⌈\frac{(n-3)(n-4)}{6}⌉\hfill & \text{if}n\ge 3\text{and}n\ne 7\hfill \\ 3\hfill & \text{if}n=7.\hfill \end{array}\right.$

(ii)	$\overline{\gamma }\left(K_{m,n}\right)=⌈\frac{(m-2)(n-2)}{2}⌉$, where $m,n\ge 2$.

Theorem 1

[8, Kuratowski’s]

The graph $G$ is planar if and only if it contains no subgraph isomorphic to $K_5$ or $K_{3,3}$ or a subdivision of one of these.

Theorem 2

[9, Theorem 3.1]

Let $(R,\mathfrak{m})$ be a finite local ring with $\left|R\right|=p^n$ for some prime $p$ and some positive integer $n\ge 2$. Then ${\Gamma }_N\left(R\right)$ is planar if and only if $R$ is isomorphic to one of the following rings: ${\mathbb{Z}}_4,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉},{\mathbb{Z}}_9$ or $\frac{{\mathbb{Z}}_3\left[x\right]}{〈x^2〉}$.

Theorem 3

[9, Theorem 3.2]

Let $R\cong R_1\times \cdots \times R_n\times F_1\times \cdots \times F_m$ be a finite commutative ring with identity, where each $(R_i,{\mathfrak{m}}_i)$ is a local ring and $F_j$ is a field, $m,n\ge 1$ and $m+n\ge 2$. Then ${\Gamma }_N\left(R\right)$ is planar if and only if $R$ is isomorphic to one of the following rings: ${\mathbb{Z}}_4\times {\mathbb{Z}}_2$ or $\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_2$.

Theorem 4

[9]

Let $R\cong F_1\times F_2\times \cdots \times F_n$ be a finite ring, where each $F_i$ is a field and $n\ge 2$. Then $\Gamma \left(R\right)$ is planar if and only if $R$ is isomorphic to one of the following rings: ${\mathbb{Z}}_2\times \mathbb{F},{\mathbb{Z}}_3\times \mathbb{F},{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$ or ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_3$, where $F$ is a finite field.

Theorem 5

[5]

Let $R$ be a finite ring such that $\left|\text{Spec(R)}\right|\ge 5$. Then $\overline{\gamma }\left(\Gamma \left(R\right)\right)\ge 6$.

Theorem 6

[9]

Let $(R,\mathfrak{m})$ be a finite local ring with $\left|R\right|=p^n$ for some prime $p$ and some positive integer $n\ge 2$. Then ${\Gamma }_N\left(R\right)\cong K_{\left|{\mathfrak{m}}^{\ast }\right|}+\overline{K_{\left|R^{\times }\right|}}$, where $R^{\times }=R\setminus \mathfrak{m}$ is the set of all units in $R$.

Theorem 7

[5]

Let $R$ be a finite ring such that $\left|\text{Spec(R)}\right|=2$. Then $\overline{\gamma }\left(\Gamma \left(R\right)\right)=1$ if and only if $R$ is isomorphic to one of the following 16 rings: ${\mathbb{F}}_4\times {\mathbb{F}}_4,{\mathbb{F}}_4\times {\mathbb{Z}}_5,{\mathbb{Z}}_2\times \frac{{\mathbb{F}}_4\left[x\right]}{〈x^2〉},{\mathbb{Z}}_2\times \frac{{\mathbb{Z}}_4\left[x\right]}{〈x^2+x+1〉},{\mathbb{Z}}_2\times \frac{{\mathbb{Z}}_2[x,y]}{〈x^2,xy,y^2〉},{\mathbb{Z}}_2\times \frac{{\mathbb{Z}}_4\left[x\right]}{〈2x,x^2〉},{\mathbb{Z}}_3\times {\mathbb{Z}}_8,{\mathbb{Z}}_3\times \frac{{\mathbb{Z}}_2\left[x\right]}{〈x^3〉},{\mathbb{Z}}_3\times \frac{{\mathbb{Z}}_4\left[x\right]}{〈x^2-2,x^3〉},{\mathbb{Z}}_4\times {\mathbb{Z}}_5,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_5,{\mathbb{F}}_4\times {\mathbb{Z}}_4,{\mathbb{F}}_4\times \frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉},{\mathbb{Z}}_4\times {\mathbb{Z}}_4,{\mathbb{Z}}_4\times \frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉},\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times \frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}$.

Theorem 8

[5]

Let $R$ be a finite ring such that $\left|\text{Spec(R)}\right|=3$. Then $\overline{\gamma }\left(\Gamma \left(R\right)\right)=1$ if and only if $R$ is isomorphic to one of the following 6 rings: ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{F}}_4,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_4,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times \frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉},{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_5,{\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{Z}}_3,{\mathbb{Z}}_3\times {\mathbb{Z}}_3\times {\mathbb{Z}}_3$.

Theorem 9

[5]

Let $R$ be a finite ring such that $\left|\text{Spec(R)}\right|=4$. Then $\overline{\gamma }\left(\Gamma \left(R\right)\right)=1$ if and only if $R$ is isomorphic to ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$.

Theorem 10

[10]

Suppose $m\ge 0,n\ge 0$, and $m\ge n-1$. The non-orientable genus of ${\overline{K}}_m+K_n$ is given by $\overline{\gamma }({\overline{K}}_m+K_n)=\left\{\begin{array}{cc}0\hfill & \text{if}n\le 2\hfill \\ ⌈\frac{(m-2)(n-2)}{2}⌉\hfill & \text{if}n\ge 2\text{and}(m,n)\ne (4,5),\hfill \\ 4\hfill & \text{if}(m,n)=(4,5).\hfill \end{array}\right.$

Theorem 11

[11]

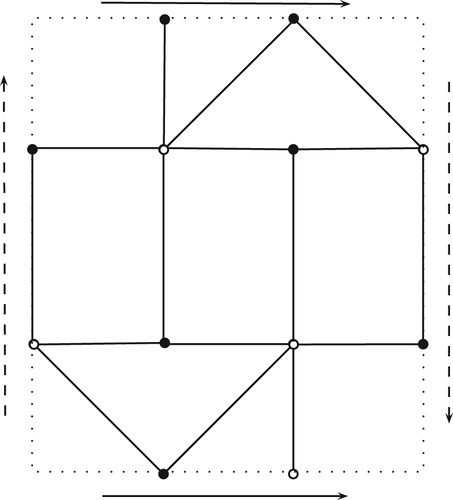
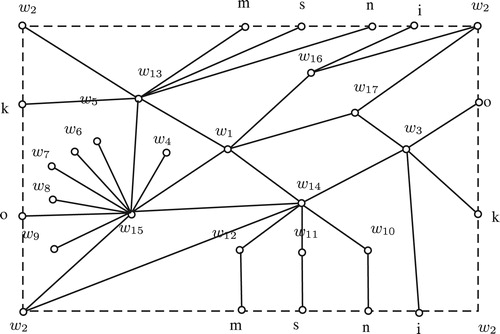
The complete bipartite graph $K_{3,5}$ admits the unique embedding into the Klein bottle, up to congruence, as shown in Fig. 1 .

Fig. 1 The unique embedding of $K_{3,5}$ on the Klein bottle.

2 Crosscap of ${\Gamma }_N\left(R\right)$

In this section, we classify all finite rings (up to isomorphism) with identity whose nilpotent graphs can be embedded in a projective plane or Klein bottle.

The following Lemma gives the general formula for the crosscap of the graph ${\Gamma }_N\left(R\right)$ in the case of local ring.

Lemma 2

If $(R,\mathfrak{m})$ is a finite local ring with $\left|R\right|=\alpha$ and $\left|\mathfrak{m}\right|=\beta \ge 4$, then $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=⌈\frac{(\alpha -\beta -2)(\beta -3)}{2}⌉$.

Proof

By Theorem 6, ${\Gamma }_N\left(R\right)\cong \overline{K_{\left|R^{\times }\right|}}+K_{\left|{\mathfrak{m}}^{\ast }\right|}$. Also $\left|R^{\times }\right|\ge \left|{\mathfrak{m}}^{\ast }\right|-1\ge 2$ and $(\left|R^{\times }\right|,\left|{\mathfrak{m}}^{\ast }\right|)\ne (4,5)$. By Theorem 10, $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=\overline{\gamma }(\overline{K_{\left|R^{\times }\right|}}+K_{\left|{\mathfrak{m}}^{\ast }\right|})=\overline{\gamma }\left(K_{\left|R^{\times }\right|,\left|{\mathfrak{m}}^{\ast }\right|}\right)=⌈\frac{(\alpha -\beta -2)(\beta -3)}{2}⌉$.

Lemma 3

If $R\cong R_1\times R_2\times \cdots \times R_n(n\ge 2)$ is a finite commutative ring with identity, where $R_i$’s are local rings which are not fields, then $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge 5$.

Proof

Since ${\Gamma }_N({\mathbb{Z}}_4\times {\mathbb{Z}}_4)$ is a subgraph of ${\Gamma }_N\left(R\right)$, ${\Gamma }_N\left(R\right)$ contains a copy of $K_{4,7}$ which is a subgraph of the graph induced by the set of vertices $[(R_1^{\times }\times {\mathfrak{m}}_2)\cup ({\mathfrak{m}}_1\times R_2^{\times })\cup ({\mathfrak{m}}_1\times {\mathfrak{m}}_2)]\setminus \left\{0_R\right\}$. By Lemma 1 $\left(ii\right)$, $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{4,7}\right)\ge 5$. Thus the result follows.□

We consider the finite ring $R$ and so $R\cong R_1\times R_2\times \cdots \times R_n$ where $R_i$ is a local ring. On the observation of Lemma 3, at least one $R_i$ is a field, for some $i$.

Lemma 4

Let $R\cong F_1\times \cdots \times F_n$ be a finite commutative ring with identity, where each $F_j$ is a field, $n\ge 2$ and $\left|F_1\right|\le \left|F_2\right|\le \cdots \le \left|F_n\right|$. Then $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge 3$ if one of the following holds:

$\left(i\right)n\ge 5$

$\left(ii\right)n=4$ and $\left|F_4\right|\ge 3$

$\left(iii\right)n=3,\left|F_1\right|\ge 3$, and either $F_2\ncong {\mathbb{Z}}_3$ or $F_3\ncong {\mathbb{Z}}_3$

$\left(iv\right)n=3,\left|F_1\right|=2=\left|F_2\right|$ and $\left|F_3\right|\ge 8$

$\left(v\right)n=3,\left|F_1\right|=2,\left|F_2\right|=3$ and $\left|F_3\right|\ge 5$

$\left(vi\right)n=3,\left|F_1\right|=2$ and $\left|F_2\right|\ge 4$.

Proof

(i)	Follows from Theorem 5.

(ii)

Suppose $n=4$ and $\left|F_4\right|\ge 3$. Then since ${\Gamma }_N({\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_3)$ is a subgraph of ${\Gamma }_N\left(R\right)$, ${\Gamma }_N\left(R\right)$ contains a copy of $K_{3,5}$ which is a subgraph of a graph induced by set of vertices $[({\mathbb{Z}}_2\times {\mathbb{Z}}_2\times 0\times 0)\cup (0\times 0\times {\mathbb{Z}}_2\times {\mathbb{Z}}_3)]\setminus \left\{0_R\right\}$. It then follows from Lemma 1 $\left(ii\right)$ that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{3,5}\right)\ge 2$. We claim that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ne 2$. By Theorem 11, $K_{3,5}$ has a unique embedding in ${\mathcal{N}}_2$. The embedding of $K_{3,5}$ in ${\mathcal{N}}_2$ has six 4-faces and one 6 face. Consider the face $f^{\ast }$ of length six. Let $V_i$ be the partition of $K_{3,5}$, for $i=1,2$. Then $f^{\ast }$ contains exactly 3 vertices from $V_i$ for all $i$. In order to embed the set of vertices $S=\{(0,1,1,0),(1,0,0,1),(1,0,0,2)\}$, we have to choose the face $f^{\ast }$ of length 6. Clearly $N\left(S\right)=\{(1,0,0,0),(0,1,0,0),(0,0,0,1),(0,0,0,2),(0,0,1,0)\}$. If $f^{\ast }$ contains all the vertices from $N\left(S\right)$, then the vertices of $N\left(S\right)$ that are adjacent to the vertices $(0,1,1,0),(1,0,0,1)$ and $(1,0,0,2)$ make two edge crossings where $N\left(S\right)$ denote the set of vertices adjacent to the vertices of $S$. If $f^{\ast }$ does not contain all the elements of $N\left(S\right)$, then we cannot insert the vertices of $S$ without crossing. Thus we cannot embed ${\Gamma }_N\left(R\right)$ in ${\mathcal{N}}_2$. Hence $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge 3$.

(iii)

Suppose $n=3,\left|F_1\right|\ge 3$, and either $F_2\ncong {\mathbb{Z}}_3$ or $F_3\ncong {\mathbb{Z}}_3$. Then ${\Gamma }_N({\mathbb{Z}}_3\times {\mathbb{Z}}_3\times {\mathbb{F}}_4)$ is a subgraph of ${\Gamma }_N\left(R\right)$. So ${\Gamma }_N\left(R\right)$ contains a copy of $K_{3,8}$ with vertex set $[(0\times 0\times {\mathbb{F}}_4)\cup ({\mathbb{Z}}_3\times {\mathbb{Z}}_3\times 0)]\setminus \left\{0_R\right\}$. It then follows from Lemma 1 $\left(ii\right)$ that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{3,8}\right)\ge 3$. By Theorem 8, $\overline{\gamma }\left({\Gamma }_N({\mathbb{Z}}_3\times {\mathbb{Z}}_3\times {\mathbb{Z}}_3)\right)=1$.

(iv)

Suppose $\left|F_1\right|=2=\left|F_2\right|,\left|F_3\right|\ge 8$ and $n=3$. Then since ${\Gamma }_N({\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{F}}_8)$ is a subgraph of ${\Gamma }_N\left(R\right)$, ${\Gamma }_N\left(R\right)$ contains a copy of $K_{3,7}$ with vertex set $[({\mathbb{Z}}_2\times {\mathbb{Z}}_2\times 0)\cup (0\times 0\times {\mathbb{F}}_8)]\setminus \left\{0_R\right\}$. It then follows from Lemma 1 $\left(ii\right)$ that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{3,7}\right)\ge 3$.

(v)

Suppose $\left|F_1\right|=2,\left|F_2\right|=3,\left|F_3\right|\ge 5$ and $n=3$. Then since ${\Gamma }_N({\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{Z}}_5)$ is a subgraph of ${\Gamma }_N\left(R\right)$, ${\Gamma }_N\left(R\right)$ contains a copy of $K_{4,5}$ with vertex set $[({\mathbb{Z}}_2\times {\mathbb{Z}}_3\times 0)\cup (0\times 0\times {\mathbb{Z}}_5)]\setminus \left\{0_R\right\}$. It then follows from Lemma 1 $\left(ii\right)$ that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{4,5}\right)\ge 3$.

(vi)

Suppose $\left|F_1\right|=2,\left|F_2\right|\ge 4$ and $n=3$. Then since ${\Gamma }_N({\mathbb{Z}}_2\times {\mathbb{F}}_4\times {\mathbb{F}}_4)$ is a subgraph of ${\Gamma }_N\left(R\right)$, ${\Gamma }_N\left(R\right)$ contains a copy of $K_{3,7}$ with vertex set $[(0\times 0\times {\mathbb{F}}_4)\cup ({\mathbb{Z}}_2\times {\mathbb{F}}_4\times 0)]\setminus \left\{0_R\right\}$. It then follows from Lemma 1 $\left(ii\right)$ that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{3,7}\right)\ge 3$.□

The following Theorems characterize the ring $R$ for which $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=1$ and $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=2$.

Theorem 12

Let $R$ be a finite ring. Then $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=1$ if and only if $R$ is isomorphic to one of the following rings:

${\mathbb{Z}}_8,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^3〉},\frac{{\mathbb{Z}}_4\left[x\right]}{〈2x,x^2-2〉},\frac{{\mathbb{Z}}_2[x,y]}{{〈x,y〉}^2},\frac{{\mathbb{Z}}_4\left[x\right]}{{〈2,x〉}^2},{\mathbb{Z}}_4\times {\mathbb{Z}}_3,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_3,{\mathbb{F}}_4\times {\mathbb{F}}_4,{\mathbb{F}}_4\times {\mathbb{Z}}_5,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{F}}_4,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_5,{\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{Z}}_3,{\mathbb{Z}}_3\times {\mathbb{Z}}_3\times {\mathbb{Z}}_3$ or ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$.

Proof

Assume that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=1$. Then by Theorem 5, $\left|\text{Spec(R)}\right|\le 4$. Since $R$ is finite, $R\cong R_1\times R_2\times \cdots \times R_n$, where $(R_i,{\mathfrak{m}}_i)$ is a local ring for each $i$. Without loss of generality, assume that $\left|R_1\right|\le \left|R_2\right|\le \cdots \le \left|R_n\right|$. If $\left|\text{Spec(R)}\right|=4$, then by Lemma 4 $\left(ii\right)$, $R\cong {\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$.

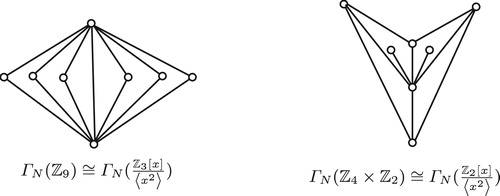
Case 1: $\left|\text{Spec(R)}\right|=3$.

If $R_i$ is a field for all $i$, then ${\Gamma }_N\left(R\right)\cong \Gamma \left(R\right)$ and so by Theorem 8, $R$ is isomorphic to one of the following rings: ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{F}}_4,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_5,{\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{Z}}_3,{\mathbb{Z}}_3\times {\mathbb{Z}}_3\times {\mathbb{Z}}_3$. If not, without loss of generality, let $R_1$ be a local ring but not a field. Then ${\Gamma }_N({\mathbb{Z}}_4\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2)$ is a subgraph of ${\Gamma }_N\left(R\right)$. So ${\Gamma }_N\left(R\right)$ contains a copy of $K_{3,6}$ which is the subgraph of a graph induced by the set of vertices $[({\mathbb{Z}}_4\times 0\times 0)\cup ({\mathfrak{m}}_1\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2)]\setminus \left\{0_R\right\}$. It then follows from Lemma 1 $\left(ii\right)$ that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{3,6}\right)\ge 2$, a contradiction.

Case 2: $\left|\text{Spec(R)}\right|=2$.

If $R_i$ is a field, then ${\Gamma }_N\left(R\right)\cong \Gamma \left(R\right)$ and so by Theorem 7, $R\cong {\mathbb{F}}_4\times {\mathbb{F}}_4$ or ${\mathbb{F}}_4\times {\mathbb{Z}}_5$. If not, without loss of generality, let $R_1$ be a local ring but not a field. We claim that $\left|{\mathfrak{m}}_1^{\ast }\right|=1$ and $\left|R_2\right|\le 3$.

Suppose that $\left|{\mathfrak{m}}_1^{\ast }\right|\ge 2$. Then let $z_1=(b_1,0),z_2=(b_2,0),z_3=(u_1,0),z_4=(u_2,0),z_5=(u_3,0),z_6=(b_1,1),z_7=(b_2,1)$ and $z_8=(0,1)$, where $b_1,b_2\in {\mathfrak{m}}_1^{\ast },u_i\in R_1^{\times }$ for $1\le i\le 3$. Then ${\Gamma }_N\left(R\right)$ contains a copy of $K_{3,5}$ which is the subgraph of the graph induced by set of vertices $\{z_1,\dots ,z_8\}$ and so $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{3,5}\right)\ge 2$, a contradiction. Hence $\left|{\mathfrak{m}}_1^{\ast }\right|=1$ and so $\left|R_1\right|=4$.

Suppose that $\left|R_2\right|\ge 4$. Then let $z\in {\mathfrak{m}}_1^{\ast }$ and $y_1=(z,0),y_2=(u_1,0),y_3=(u_2,0),y_4=(0,v_1),y_5=(0,v_2),y_6=(0,v_3),y_7=(z,v_1),y_8=(z,v_2),y_9=(z,v_3)$ where $u_1,u_2\in R_1^{\times }$ and $v_i\in R_2^{\ast }$ for all $i$. Then ${\Gamma }_N\left(R\right)$ contains a copy of $K_{3,6}$ which is the subgraph of the graph induced by set of vertices $\{y_1,\dots ,y_9\}$. It then follows from Lemma 1 $\left(ii\right)$ that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{3,6}\right)\ge 2$, a contradiction. Hence $\left|R_2\right|\le 3$.

Thus we get $R\cong {\mathbb{Z}}_4\times {\mathbb{Z}}_2,{\mathbb{Z}}_4\times {\mathbb{Z}}_3,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_2,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_3$. By Theorem 3, ${\Gamma }_N\left(R\right)$ is planar for $R\cong {\mathbb{Z}}_4\times {\mathbb{Z}}_2,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_2$. Hence we conclude that $R\cong {\mathbb{Z}}_4\times {\mathbb{Z}}_3$ or $\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_3$.

Case 3: $\left|\text{Spec(R)}\right|=1$.

If $\left|{\mathfrak{m}}_1\right|\le 3$, then by Theorem 2, ${\Gamma }_N\left(R\right)$ is planar. Hence $\left|{\mathfrak{m}}_1\right|\ge 4$. Now by Lemma 2, $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=⌈\frac{(\alpha -\beta -2)(\beta -3)}{2}⌉$, where $\left|R\right|=\alpha$ and $\left|\mathfrak{m}\right|=\beta$. Since $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=1$, $\left|R\right|=8$ and $\left|\mathfrak{m}\right|=4$. So $R$ is isomorphic to one of the following rings: ${\mathbb{Z}}_8,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^3〉},\frac{{\mathbb{Z}}_4\left[x\right]}{〈2x,x^2-2〉},\frac{{\mathbb{Z}}_2[x,y]}{{〈x,y〉}^2}$ or $\frac{{\mathbb{Z}}_4\left[x\right]}{{〈2,x〉}^2}$.

Conversely, suppose $R$ is isomorphic to one of the following rings: ${\mathbb{Z}}_8,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^3〉},\frac{{\mathbb{Z}}_4\left[x\right]}{〈2x,x^2-2〉},\frac{{\mathbb{Z}}_2[x,y]}{{〈x,y〉}^2}$ or $\frac{{\mathbb{Z}}_4\left[x\right]}{{〈2,x〉}^2}$. Then by Lemma 2, $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=1$.

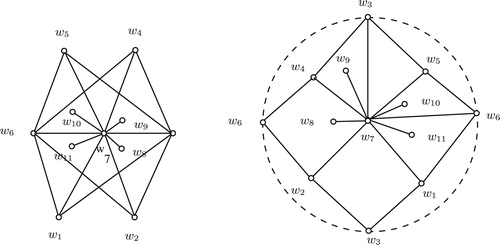
If $R\cong {\mathbb{Z}}_4\times {\mathbb{Z}}_3$ or $\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_3$, then by Theorem 3, ${\Gamma }_N\left(R\right)$ is non-planar. Moreover Fig. 2 shows one explicit embedding of ${\Gamma }_N\left(R\right)$ in the projective plane. Thus $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=1$.

Suppose $R$ is isomorphic to one of the following rings: ${\mathbb{F}}_4\times {\mathbb{F}}_4,{\mathbb{F}}_4\times {\mathbb{Z}}_5,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{F}}_4,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_5,{\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{Z}}_3,{\mathbb{Z}}_3\times {\mathbb{Z}}_3\times {\mathbb{Z}}_3$ or ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$. Then by Theorems 7 – 9, $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=1$. This completes the proof.□

Fig. 2 Embedding of ${\Gamma }_N({\mathbb{Z}}_4\times {\mathbb{Z}}_3)\cong {\Gamma }_N(\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_3)$ in ${\mathcal{N}}_1$.

Theorem 13

Let $R$ be a finite ring. Then $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=2$ if and only if $R$ is isomorphic to one of the following rings: ${\mathbb{Z}}_4\times {\mathbb{F}}_4,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{F}}_4,{\mathbb{F}}_4\times {\mathbb{Z}}_7,{\mathbb{Z}}_5\times {\mathbb{Z}}_5,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_7$ or ${\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{F}}_4$.

Proof

Assume that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=2$. Then by Theorem 5, $\left|\text{Spec(R)}\right|\le 4$. Since $R$ is finite, $R\cong R_1\times R_2\times \cdots \times R_n$, where $(R_i,{\mathfrak{m}}_i)$’s are local ring for each $i$. Without loss of generality, assume that $\left|R_1\right|\le \left|R_2\right|\le \cdots \le \left|R_n\right|$.

Case 1: $\left|\text{Spec(R)}\right|=4$.

Then by Lemma 4 $\left(ii\right)$, $R\cong {\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$. Also, by Theorem 12, $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=1$. Thus there is no ring available in this case.

Case 2: $\left|\text{Spec(R)}\right|=3$.

If $R_i$ is a field for all $i$, then by Lemma 4 $\left(iii\right)$–$\left(vi\right)$, $R$ is isomorphic to one of the following rings: ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_3,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{F}}_4,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_5,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_7,{\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{Z}}_3,{\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{F}}_4,{\mathbb{Z}}_3\times {\mathbb{Z}}_3\times {\mathbb{Z}}_3$.

$\left(i\right)$ If $R$ is isomorphic to ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$, then ${\Gamma }_N\left(R\right)\cong \Gamma \left(R\right)$ and so by Theorem 4, ${\Gamma }_N\left(R\right)$ is planar.

$\left(ii\right)$ If $R$ is isomorphic to one of the following rings: ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_3,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{F}}_4,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_5,{\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{Z}}_3,{\mathbb{Z}}_3\times {\mathbb{Z}}_3\times {\mathbb{Z}}_3$, then by Theorem 12, $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=1$.

Thus $R$ is isomorphic to the following rings: ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_7,{\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{F}}_4$.

Suppose that at least one $R_i$ is not a field. Without loss of generality, let $R_1$ be a local ring but not a field. Then ${\Gamma }_N({\mathbb{Z}}_4\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2)$ is a subgraph of ${\Gamma }_N\left(R\right)$. So ${\Gamma }_N\left(R\right)$ contains a copy of $K_{3,6}$ which is the subgraph of a graph induced by the set of vertices $[({\mathbb{Z}}_4\times 0\times 0)\cup (\mathfrak{m}\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2)]\setminus \left\{0_R\right\}$. It then follows from Lemma 1 $\left(ii\right)$ that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{3,6}\right)\ge 2$. We claim that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ne 2$. By Theorem 11, $K_{3,5}$ has a unique embedding in ${\mathcal{N}}_2$ and it has six 4-faces and one 6-face. Hence we can find a unique embedding of $K_{3,6}$ in ${\mathcal{N}}_2$ that contains nine 4-faces. Let $V_i$ be a partition of $K_{3,6}$ for $i=1,2$. Then each face contains exactly two vertices from $V_i$. Also each $v$ from $V_2$ lie in exactly 3 faces. So there may be at most one face that contains the vertices $\{(0,1,0),(2,0,0),(2,1,0)\}$. Suppose there exists a face that contains the vertices $\{(0,1,0),(2,0,0),(2,1,0)\}$. Since $(1,0,1)$ and $(3,0,1)$ are adjacent to these vertices in ${\Gamma }_N\left(R\right)$, there must be one edge crossing in the embedding of ${\Gamma }_N\left(R\right)$. Suppose not. Then we cannot insert that vertices without crossing. Hence we cannot have the embedding of ${\Gamma }_N\left(R\right)$ in the non-orientable surface of crosscap 2. Thus $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge 3$, a contradiction.

Case 3: $\left|\text{Spec(R)}\right|=2$.

If $R_i$ is a field, then ${\Gamma }_N\left(R\right)\cong K_{\left|F_1^{\ast }\right|,\left|F_2^{\ast }\right|}$. Since $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=2,\left|F_1\right|=4,\left|F_2\right|=7$ or $\left|F_1\right|=5=\left|F_2\right|$. Hence $R\cong {\mathbb{F}}_4\times {\mathbb{Z}}_7$ or ${\mathbb{Z}}_5\times {\mathbb{Z}}_5$. If not, then at least one $R_i$ is not a field. Without loss of generality, let $R_1$ be a local ring but not a field. We claim that $\left|{\mathfrak{m}}_1^{\ast }\right|=1$ and $\left|R_2\right|\le 4$.

Suppose that $\left|{\mathfrak{m}}_1^{\ast }\right|=2$. Then $R_1\cong {\mathbb{Z}}_9$ or $\frac{{\mathbb{Z}}_3\left[x\right]}{〈x^2〉}$. Let $b_1,b_2\in {\mathfrak{m}}_1^{\ast }$. Let $z_1=(b_1,0),z_2=(b_2,0),z_3=(u_1,0),z_4=(u_2,0),z_5=(u_3,0),z_6=(b_1,1),z_7=(b_2,1),z_8=(0,1),z_9=(u_4,0),z_{10}=(u_5,0)$and $z_{11}=(u_6,0)$, where $u_i\in R_1^{\times }$ for $1\le i\le 6$. Then ${\Gamma }_N\left(R\right)$ contains a copy of $K_{5,6}$ which is the subgraph of the graph induced by set of vertices $\{z_1,\dots ,z_{11}\}$ and so $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{5,6}\right)\ge 6$, a contradiction. Hence $\left|{\mathfrak{m}}_1^{\ast }\right|=1$ or $\left|{\mathfrak{m}}_1^{\ast }\right|\ge 3$.

Suppose that $\left|{\mathfrak{m}}_1^{\ast }\right|\ge 3$. Then ${\Gamma }_N\left(R\right)$ contains a copy of $K_{4,7}$ which consists of vertices of $[\{(a,0):a\in R_1^{\times }\}\cup \{(b,1),(b,0):b\in {\mathfrak{m}}_1^{\ast }\}]\setminus \left\{0_R\right\}$. It then follows from Lemma 1 $\left(ii\right)$ that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{4,7}\right)\ge 5$, which contradicts our assumption. Therefore $\left|{\mathfrak{m}}_1^{\ast }\right|=1$ and so $\left|R_1\right|=4$.

Suppose that $\left|R_2\right|\ge 5$. Then let $z\in {\mathfrak{m}}_1^{\ast }$ and $y_1=(z,0),y_2=(u_1,0),y_3=(u_2,0),y_4=(0,v_1),y_5=(0,v_2),y_6=(0,v_3),y_7=(0,v_4),y_8=(z,v_1),y_9=(z,v_2),y_{10}=(z,v_3),y_{11}=(z,v_4)$ where $u_1,u_2\in R_1^{\times }$ and $v_i\in R_2^{\ast }$ for all $i$. Then ${\Gamma }_N\left(R\right)$ contains a copy of $K_{3,8}$ which is the subgraph of the graph induced by set of vertices $\{y_1,\dots ,y_{11}\}$. It then follows from Lemma 1 $\left(ii\right)$ that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{3,8}\right)\ge 3$, a contradiction. Hence $\left|R_2\right|\le 4$.

Thus we get $R$ is isomorphic to one of the following rings: ${\mathbb{Z}}_4\times {\mathbb{Z}}_2,{\mathbb{Z}}_4\times {\mathbb{Z}}_3,{\mathbb{Z}}_4\times {\mathbb{F}}_4,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_2,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_3,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{F}}_4$. By Theorem 2, ${\Gamma }_N\left(R\right)$ is planar for $R\cong {\mathbb{Z}}_4\times {\mathbb{Z}}_2,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_2$. Also, by Theorem 12, $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=1$ for $R\cong {\mathbb{Z}}_4\times {\mathbb{Z}}_3,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_3$. Hence we conclude that $R\cong {\mathbb{Z}}_4\times {\mathbb{F}}_4$ or $\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{F}}_4$.

Conversely, suppose that $R\cong {\mathbb{F}}_4\times {\mathbb{Z}}_7$ or ${\mathbb{Z}}_5\times {\mathbb{Z}}_5$. Then since ${\Gamma }_N\left(R\right)\cong K_{\left|F_1^{\ast }\right|,\left|F_2^{\ast }\right|}$, by Lemma 1 $\left(ii\right)$, $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=2$.

Assume that $R$ is isomorphic to one of the following rings: ${\mathbb{Z}}_4\times {\mathbb{F}}_4$ or $\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{F}}_4$.

Then since ${\Gamma }_N({\mathbb{Z}}_4\times {\mathbb{F}}_4)\cong {\Gamma }_N(\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{F}}_4)$, ${\Gamma }_N\left(R\right)$ contains a copy of $K_{3,6}$ which is the subgraph of the graph induced by the set of vertices $[({\mathbb{Z}}_4\times 0)\cup (\mathfrak{m}\times F_4)]\setminus \left\{0_R\right\}$. By Lemma 1 $\left(ii\right)$, $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{3,6}\right)\ge 2$. Moreover Fig. 3 shows one explicit embedding of ${\Gamma }_N\left(R\right)$ in ${\mathcal{N}}_2$. Thus $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=2$.

Assume that $R$ is isomorphic to ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_7$. Then let $r_i=(0,0,i),r_{6+i}=(0,1,i),r_{12+i}=(1,0,i),r_{19}=(0,1,0),r_{20}=(1,0,0)$ and $r_{21}=(1,1,0)$ for $1\le i\le 6$. Then ${\Gamma }_N\left(R\right)$ contains a copy of $K_{3,6}$ which consists of vertices $\{r_1,\dots ,r_6,r_{19},r_{20},r_{21}\}$. It then follows from Lemma 1 $\left(ii\right)$ that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{3,6}\right)\ge 2$. Moreover Fig. 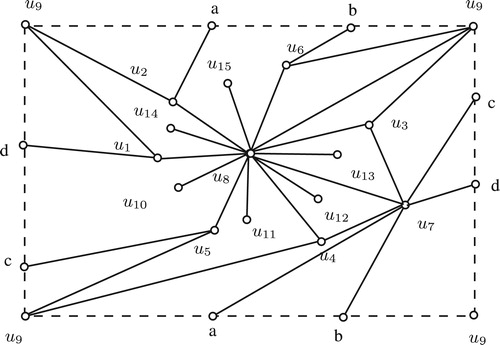4 shows the embedding in the non-orientable surface of crosscap 2. Thus $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=2$.

Suppose that $R\cong {\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{F}}_4$. Then let $w_i=(0,0,a_i),w_{3+i}=(0,1,a_i),w_{6+i}=(0,2,a_i),w_{9+i}=(1,0,a_i),w_{13}=(0,1,0),w_{14}=(0,2,0),w_{15}=(1,0,0),w_{16}=(1,1,0),w_{17}=(1,2,0)$ for $1\le i\le 3$. Then ${\Gamma }_N\left(R\right)$ contains a copy of $K_{3,5}$ which consists of vertices $\{w_1,w_2,w_3,w_{13},w_{14},w_{15},w_{16},w_{17}\}$. It then follows from Lemma 1 $\left(ii\right)$ that $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)\ge \overline{\gamma }\left(K_{3,5}\right)\ge 2$. 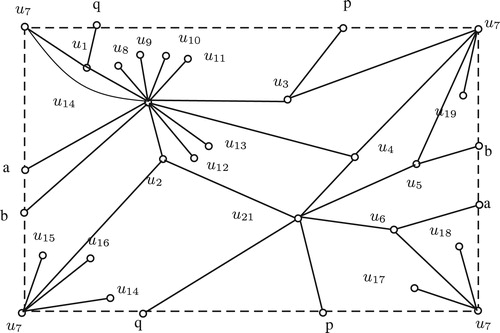Moreover Fig. 5 shows one explicit embedding of ${\Gamma }_N\left(R\right)$ in the non-orientable surface of crosscap 2. Thus $\overline{\gamma }\left({\Gamma }_N\left(R\right)\right)=2$. This completes the proof.□

Fig. 3 Embedding of ${\Gamma }_N({\mathbb{Z}}_4\times {\mathbb{F}}_4)\cong {\Gamma }_N(\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{F}}_4)$ in ${\mathcal{N}}_2$.

Fig. 4 Embedding of ${\Gamma }_N({\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_7)$ in ${\mathcal{N}}_2$.

Fig. 5 Embedding of ${\Gamma }_N({\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{F}}_4)$ in ${\mathcal{N}}_2$.

3 Outerplanarity of ${\Gamma }_N\left(R\right)$

Let $G$ be a graph with $n$ vertices and $q$ edges. A chord is any edge of $G$ joining two nonadjacent vertices in a cycle of $G$. Let $C$ be a cycle of $G$. We say $C$ is a primitive cycle if it has no chords. Also, a graph $G$ has the primitive cycle property (PCP) if any two primitive cycles intersect in at most one edge. The number $frank\left(G\right)$ is called the free rank of $G$ and it is the number of primitive cycles of $G$. Also, the number $rank\left(G\right)=q-n+r$ is called the cycle rank of $G$, where $r$ is the number of connected components of $G$. The cycle rank of $G$ can be expressed as the dimension of the cycle space of $G$. By [12, Proposition 2.2], we have $rank\left(G\right)\le frank\left(G\right)$. A graph $G$ is called a ring graph if it satisfies one of the following equivalent conditions (see [9]).

$\left(i\right)$ rank(G) = frank(G),

$\left(ii\right)$ $G$ satisfies the PCP and $G$ does not contain a subdivision of $K_4$ as a subgraph.

The following concepts were defined in [13]. An embedding $\varphi$ of a planar graph is 1-outerplanar if it is outerplanar (i.e.) all vertices are incident on the outerface in $\varphi$. An embedding of a planar graph is $k$-outerplanar if removing all vertices on the outerface (together with their incident edges) yields a $(k-1)$-outerplanar embedding. A graph is $k$-outerplanar if it has a $k$-outerplanar embedding. The outerplanarity index of a graph $G$ is the smallest $k$ such that $G$ is $k$-outerplanar. There is a characterization for outerplanar graphs that says a graph is outerplanar if and only if it does not contain a subdivision of $K_4$ or $K_{2,3}$. Clearly, every outerplanar graph is a ring graph or every ring graph is a planar graph. In this section, we characterize all rings R such that ${\Gamma }_N\left(R\right)$ is a ring graph and outerplanar graph with index 1,2.

Theorem 14

Let $R$ be a finite ring. Then ${\Gamma }_N\left(R\right)$ is a ring graph if and only if $R$ is isomorphic to one of the following rings:

${\mathbb{Z}}_4,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉},{\mathbb{Z}}_9,\frac{{\mathbb{Z}}_3\left[x\right]}{〈x^2〉},{\mathbb{Z}}_4\times {\mathbb{Z}}_2,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_2,{\mathbb{Z}}_2\times \mathbb{F},{\mathbb{Z}}_3\times {\mathbb{Z}}_3$ or ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$.

Proof

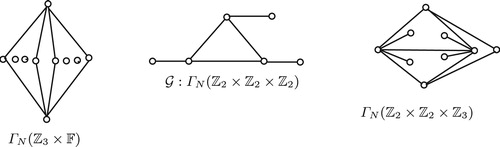
Assume that ${\Gamma }_N\left(R\right)$ is a ring graph. Then since every ring graph is planar, it is enough to check rings in Theorems 2–4, whether it is a ring graph or not. Now the nilpotent graph of rings ${\mathbb{Z}}_4,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉},{\mathbb{Z}}_9,\frac{{\mathbb{Z}}_3\left[x\right]}{〈x^2〉},{\mathbb{Z}}_4\times {\mathbb{Z}}_2,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_2,{\mathbb{Z}}_2\times \mathbb{F},{\mathbb{Z}}_3\times {\mathbb{Z}}_3,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2,$we have that $rank\left({\Gamma }_N\left(R\right)\right)=frank\left({\Gamma }_N\left(R\right)\right)$, and so they are ring graphs. Also for rings ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_3,{\mathbb{Z}}_3\times \mathbb{F}$, where $\left|F\right|\ge 4$, ${\Gamma }_N\left(R\right)$ contains a subdivision of $K_4$ or does not satisfy PCP (see Fig. 6) and so they are not ring graphs. The converse is obvious.□

short-legendFig. 6

Theorem 15

Let $R$ be a finite ring. Then ${\Gamma }_N\left(R\right)$ is an outerplanar if and only if $R$ is isomorphic to one of the following rings: ${\mathbb{Z}}_4,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉},{\mathbb{Z}}_2\times \mathbb{F},{\mathbb{Z}}_3\times {\mathbb{Z}}_3\text{or}{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2.$

Proof

Assume that ${\Gamma }_N\left(R\right)$ is an outerplanar. Then since ${\Gamma }_N\left(R\right)$ is a ring graph, by Theorem 14, we need to check rings ${\mathbb{Z}}_4,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉},{\mathbb{Z}}_9,\frac{{\mathbb{Z}}_3\left[x\right]}{〈x^2〉},{\mathbb{Z}}_4\times {\mathbb{Z}}_2,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_2,{\mathbb{Z}}_2\times \mathbb{F},{\mathbb{Z}}_3\times {\mathbb{Z}}_3,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$are outerplanar or not. By Fig. 7, we can find the subdivision of $K_{2,3}$ in ${\Gamma }_N\left(R\right)$ for rings ${\mathbb{Z}}_9,\frac{{\mathbb{Z}}_3\left[x\right]}{〈x^2〉},{\mathbb{Z}}_4\times {\mathbb{Z}}_2,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_2$ and so are not outerplanar. Also, the nilpotent graph for rings ${\mathbb{Z}}_4,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉},{\mathbb{Z}}_2\times \mathbb{F},{\mathbb{Z}}_3\times {\mathbb{Z}}_3,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$, is $P_3,K_{1,q-1},C_4$ or $\mathcal{G}$ (see Fig. 6) respectively and so are outerplanar. The converse is obvious.□

short-legendFig. 7

Theorem 16

Let $R$ be a finite ring. Then ${\Gamma }_N\left(R\right)$ has an outerplanarity index 2 if and only if $R$ is isomorphic to one of the following rings:

${\mathbb{Z}}_9,\frac{{\mathbb{Z}}_3\left[x\right]}{〈x^2〉},{\mathbb{Z}}_4\times {\mathbb{Z}}_2,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_2,{\mathbb{Z}}_3\times \mathbb{F},{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_3,\left|F\right|\ge 4$.

Proof

Assume that ${\Gamma }_N\left(R\right)$ has an outerplanarity index 2. Then ${\Gamma }_N\left(R\right)$ is planar, by Theorems 2–4, we need only to check rings: ${\mathbb{Z}}_4,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉},{\mathbb{Z}}_9,\frac{{\mathbb{Z}}_3\left[x\right]}{〈x^2〉},{\mathbb{Z}}_4\times {\mathbb{Z}}_2,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉}\times {\mathbb{Z}}_2,{\mathbb{Z}}_2\times \mathbb{F},{\mathbb{Z}}_3\times \mathbb{F},{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_3$. are 2-outerplanar and is minimum or not. Since ${\Gamma }_N\left(R\right)$ is not 1-outerplanar, by Theorem 15, $R$ is not isomorphic to the following rings: ${\mathbb{Z}}_4,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉},{\mathbb{Z}}_2\times \mathbb{F},{\mathbb{Z}}_3\times {\mathbb{Z}}_3,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$. By Figs. 6, 7, the nilpotent graph for rings ${\mathbb{Z}}_9,\frac{{\mathbb{Z}}_3\left[x\right]}{〈x^2〉},{\mathbb{Z}}_4\times {\mathbb{Z}}_2,\frac{{\mathbb{Z}}_2\left[x\right]}{〈x^2〉},{\mathbb{Z}}_3\times \mathbb{F},{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_3,\left|F\right|\ge 4$, are 2-outerplanar, as the removal of vertices in the outer face remains the graph $P_3$ or totally disconnected. The converse is obvious.□

Corollary 1

Let $R$ be a finite ring. Then ${\Gamma }_N\left(R\right)$ has an outerplanarity index at most two.

Notes

Peer review under responsibility of Kalasalingam University.