On n-connected splitting matroids

Peer review under responsibility of Kalasalingam University.

Abstract

In general, the splitting operation on a binary matroid $M$ does not preserve the connectivity of $M.$ In this paper, we provide sufficient conditions to preserve $n$-connectedness of a binary matroid under splitting operation. As a consequence, for an $(n+1)$-connected binary matroid $M$, we give a precise characterization of when the splitting matroid $M_T$ is $n$-connected.

Keywords:

• Splitting
• $n$-connected
• Binary matroids
• Cocircuits

1 Introduction

We refer to Oxley [1] for standard terminology in graphs and matroids. The matroids under consideration are loopless. For a matroid $M,$ let $E\left(M\right)$ and $r\left(M\right)$ denote the ground set and the rank function of $M,$ respectively. For sets $A$ and $B$, let $A\Delta B$ denote the set $(A-B)\cup (B-A).$ $G_T$.

Fleischner [2] defined the splitting operation for graphs with respect to a pair of adjacent edges. As an extension of this operation to binary matroids, Raghunathan, Shikare and Waphare [3] defined the splitting operation for binary matroids with respect to a pair of elements. The effects of the splitting operation on various parameters of a matroid like graphicness, cographicness, and connectedness have been well studied in the literature, for example,see [4–6,3,7,8^{[4][5][6][3][7][8]}].

The splitting operation for binary matroids with respect to any set $T\subset E\left(M\right),$ which is a generalization of the splitting operation with respect to a pair of elements, is defined by Shikare, Azadi and Waphare [9] as follows.

Definition 1.1

[9]

Let $M$ be a binary matroid with standard matrix representation $A$ over the field $GF\left(2\right)$ and let $T\subset E\left(M\right).$ Let $A_T$ be the matrix obtained by adjoining one extra row to the matrix $A$ whose entries are 1 in the columns labeled by the elements of the set $T$ and zero otherwise. The vector matroid of the matrix $A_T,$ denoted by $M_T,$ is called as the splitting matroid of $M$ with respect to $T,$ and the transition from $M$ to $M_T$ is called as the splitting operation with respect to $T.$ (See Remark 4.3.)

The splitting operation on a matroid $M$ is related to a lift of $M.$ A matroid $M^{\prime }$ is a coextension of $M$ if $M^{\prime }∕A\cong M$ for some nonempty subset $A$ of $E\left(M^{\prime }\right).$ If $A=1,$ then $M^{\prime }$ is a lift of $M.$ Let $M$ be a binary matroid and $T\subset E\left(M\right)$ and $M^{\prime }$ be a lift of $M$ by $a$ with $a\notin E\left(M\right)$ such that $a\cup T$ is a cocircuit in $M^{\prime }.$ Then $M^{\prime }\setminus a\cong M_T.$

In general, the splitting operation does not preserve the connectivity of a given matroid. Borse and Dhotre [5] obtained the following result to get a connected splitting matroid $M_T$ when $T=2.$

Theorem 1.2

[5]

Let $M$ be a connected and vertically $3$-connected binary matroid and $T\subset E\left(M\right)$ with $T=2.$ Suppose every cocircuit $Q$ of $M$ with $T\subset Q$ has size at least $4$ and further, $Q$ does not contain a $2$-circuit of $M$. Then $M_T$ is connected.

Malvadkar, Shikare and Dhotre [10] obtained the following generalization of Theorem 1.2 by assuming an additional condition on the girth of $M.$

Theorem 1.3

[10]

Let $n\ge 2$ be an integer and $M$ be an $n$-connected, vertically $(n+1)$-connected binary matroid with $E\left(M\right)\ge 2n+1$ and girth at least $n+1.$ Suppose $T\subset E\left(M\right)$ with $T\ge n.$ Then the matroid $M_T$ is $n$-connected if and only if for $A\subset E\left(M\right)$ with $A=n-1,$ there is a circuit $C$ in $M$ such that $C\cap T$ is odd and $C\cap A=\varnothing .$

However, in Lemma 3.7 we prove that an $n$-connected, vertically $(n+1)$-connected binary matroid $M$ with $E\left(M\right)\ge 2n+1$ and girth at least $n+1$ is $(n+1)$-connected. Therefore the matroid $M$ considered in Theorem 1.3 is actually $(n+1)$-connected, which is a stronger condition on $M$ to preserve $n$-connectedness under the splitting operation. Without assuming this stronger condition, we generalize Theorem 1.2 as follows.

Theorem 1.4

Let $n\ge 2$ be an integer and $M$ be an $n$-connected and vertically $(n+1)$-connected binary matroid with $E\left(M\right)\ge 2n+1$ and $T\subset E\left(M\right)$ with $T=n.$ Suppose $T$ is not an $n$-circuit in $M$ and for every cocircuit $Q$ of $M$ intersecting $T,$ $Q\ge max2Q\cap T,n+1$ and further, $Q\Delta T$ is not an $n$-circuit of $M.$ Then $M_T$ is $n$-connected.

We also obtain, in Theorem 4.1, some necessary conditions for $M_T$ to be $n$-connected. On combiningTheorems 1.4, 4.1, Lemma 3.7 and Theorem 1.3, we prove the following characterization for the matroid $M_T$ to be $n$-connected.

Theorem 1.5

Let $n\ge 2$ and $M$ be an $(n+1)$-connected binary matroid with $E\left(M\right)\ge 2n+1$ and $T\subset E\left(M\right)$ with $T=n.$ Then the following statements are equivalent.

(1)	The matroid $M_T$ is $n$-connected.

(2)	For every cocircuit $Q$ in $M$ intersecting $T,$ $Q\ge max2Q\cap T,n+1.$

(3)	For $A\subset E\left(M\right)$ with $A=n-1,$ there is a circuit $C$ in $M$ such that $C\cap T$ is odd and $C\cap A=\varphi .$

The circuits, cocircuits and rank function of the splitting matroid $M_T$ are given in the second section. In Section 3, we provide some basic concepts and results regarding connectedness and obtain few lemmas. The proofs of the main results are given in the last section. We also discuss the sharpness of Theorem 1.4 in the remark given at the last section.

2 Circuits and cocircuits of $M_T$

It is clear from Definition 1.1 that the ground sets of the matroids $M$ and $M_T$ are same. Further, $M=M_T$ if $T$ is a cocircuit of $M.$ Moreover, $T$ is a cocircuit of $M_T$ if no proper subset of $T$ is a cocircuit in $M.$ Mills [11] characterized the cocircuits of the splitting matroid $M_T$ in terms of the cocircuits of $M$ when $T=2.$

Theorem 2.1

[11]

Let $M$ be a binary matroid with the collection of cocircuits ${\mathcal{C}}^{\ast }$ and let $T=x,y\subset E\left(M\right).$ Suppose $T$ does not contain a cocircuit of $M.$ Then each cocircuit of $M_T$ other than $T$ belongs to one of the following collections.

(i)	${\mathcal{C}}_1^{\ast }=C^{\ast }-T:C^{\ast }\in {\mathcal{C}}^{\ast }andTisapropersubsetof{C}^{\ast }$.

(ii)	${\mathcal{C}}_2^{\ast }=C^{\ast }:C^{\ast }\in {\mathcal{C}}^{\ast }and{C}^{\ast }doesnotcontainanymemberof{\mathcal{C}}_1^{\ast }$ .

(iii)

${\mathcal{C}}_3^{\ast }=C^{\ast }\Delta T:C^{\ast }\in {\mathcal{C}}^{\ast },C^{\ast }\cap T=1and{C}^{\ast }doesnotcontainanymemberof{\mathcal{C}}_1^{\ast }.$

(iv)	${\mathcal{C}}_4^{\ast }=(C_1^{\ast }\cup C_2^{\ast })-T:C_1^{\ast },C_2^{\ast }\in {\mathcal{C}}^{\ast },C_1^{\ast }\cap C_2^{\ast }=\varphi ,x\in C_1^{\ast },y\in C_2^{\ast }and{C}_i^{\ast }$ does not contain any memberof ${\mathcal{C}}_1^{\ast }$.

Azanchiler [12] generalized Theorem 2.1 for arbitrary $T$ as follows.

Theorem 2.2

[12], pp. 35

Let $M$ be a binary matroid with the collection of cocircuits ${\mathcal{C}}^{\ast }$ and $T\subset E\left(M\right)$ with $T\ge 2.$ Suppose $T$ does not contain a cocircuit of $M.$ Then each cocircuit of $M_T$ other than $T$ belongs to one of the following collections.

(i)	${\mathcal{C}}_1^{\ast }=C^{\ast }-T:C^{\ast }\in {\mathcal{C}}^{\ast }andTisapropersubsetof{C}^{\ast }$.

(ii)	${\mathcal{C}}_2^{\ast }=C^{\ast }:C^{\ast }\in {\mathcal{C}}^{\ast }and{C}^{\ast }doesnotcontainanymemberof{\mathcal{C}}_1^{\ast }$ .

(iii)

${\mathcal{C}}_3^{\ast }=C^{\ast }\Delta T:C^{\ast }\in {\mathcal{C}}^{\ast },1\le C^{\ast }\cap T<Tand{C}^{\ast }doesnotcontainanymemberof{\mathcal{C}}_1^{\ast }.$

(iv)	${\mathcal{C}}_4^{\ast }=(C_1^{\ast }\cup C_2^{\ast }\cup \cdots \cup C_k^{\ast })-T:C_i^{\ast }\in {\mathcal{C}}^{\ast },C_i^{\ast }\cap T\ne \varphi ,C_i^{\ast }$ are mutually disjoint and none of them contains any member of ${\mathcal{C}}_1^{\ast }$.

The circuits and the rank function of the splitting matroid $M_T$ are given in [9].

Lemma 2.3

[9]

Let $M$ be a binary matroid and $T\subset E\left(M\right)$ and $\mathcal{C}$ be the collection of circuits of $M$. Then the collection of circuits of $M_T$ is ${\mathcal{C}}_1\cup {\mathcal{C}}_2$, where ${\mathcal{C}}_1=C\in \mathcal{C}:C\cap Tiseven$ and

${\mathcal{C}}_2=C_1\cup C_2:C_1,C_2\in \mathcal{C},C_1\cap C_2=\varphi ,C_i\cap Tisoddand{C}_1\cup C_{2}containsnomemberof{\mathcal{C}}_1.$

Lemma 2.4

[9]

Let $M$ be a binary matroid, $T\subset E\left(M\right)$ such that $T\ge 2$ and $T$ does not contain a cocircuit of $M.$ Suppose $r$ and $r^{\prime }$ are the rank functions of the matroid $M$ and $M_T$, respectively, and $A\subset E\left(M\right).$ Then

(i) $r^{\prime }\left(A\right)=r\left(A\right)$, if $A$ does not contain a circuit of $M$ containing an odd number of elements of $T$;

(ii) $r^{\prime }\left(A\right)=r\left(A\right)+1$, otherwise;

(iii) $r^{\prime }\left(M_T\right)=r\left(M\right)+1.$

3 Connected and vertically connected matroids

We provide here some basic definitions and results given in [1]. Let $n\ge 2$ be an integer and $M$ be a matroid with ground set $E\left(M\right)$ and rank function $r.$ An $n$-separation of $M$ is a partition $(X,Y)$ of $E\left(M\right)$ such that min$X,Y\ge n$ and $r\left(X\right)+r\left(Y\right)-r\left(M\right)\le n-1.$ If $M$ is $k$-separated for some $k,$ then connectivity $\lambda \left(M\right)$ of $M$ is the minimum $j$ such that $M$ has a $j$-separation; otherwise it is $\infty .$ An $n$-separation $(X,Y)$ of $M$ is a vertical $n$-separation if min$r\left(X\right),r\left(Y\right)\ge n.$ The vertical connectivity $k\left(M\right)$ of $M$ is the minimum $j$ such that $M$ has a vertical $j$-separation if $M$ has two disjoint cocircuits, otherwise $k\left(M\right)=r\left(M\right)$. The matroid $M$ is $n$-connected if $n\le \lambda \left(M\right)$ and it is vertically $n$-connected if $n\le k\left(M\right).$ Obviously, every $n$-connected matroid is vertically $n$-connected. If $M$ contains a circuit, then its girth, denoted by $g\left(M\right),$ is the minimum circuit size. Similarly, if $M$ contains a cocircuit, then its cogirth is the minimum cocircuit size.

We need the following known results.

Theorem 3.1

[1], pp. 279

If a matroid $M$ is not isomorphic to any uniform matroid $U_{r,\mathrm{m}}$ with $m\ge 2r-1,$ then $\lambda \left(M\right)=mink\left(M\right),g\left(M\right).$

Theorem 3.2

[1], pp. 273

If $n\ge 2$ and $M$ is an $n$-connected matroid with $E\left(M\right)\ge 2(n-1),$ then all circuits and all cocircuits of $M$ have at least $n$ elements.

Lemma 3.3

[1], pp. 274

Let $M$ be an $n$-connected matroid having at least $2n-1$ elements. Then $M$ has no $n$-element subset that is both a circuit and a cocircuit.

Lemma 3.4

[1], pp. 70

Let $M$ be a matroid and let $Y\subset E\left(M\right).$ Then $Y$ is a cocircuit if and only if $E\left(M\right)-Y$ is a hyperplane of $M.$

Corollary 3.5

[4]

Let $M$ be a matroid and let $Y\subset E\left(M\right)$ such that $r(M\setminus Y)=r\left(M\right)-1.$ Then $Y$ contains a cocircuit of $M.$

Lemma 3.6

Let $n\ge 2$ be an integer and let $M$ be an $n$-connected, vertically $(n+1)$-connected binary matroid with $E\left(M\right)\ge 2n+1.$ Then the cogirth of $M$ is at least $n+1.$

Proof

By Theorem 3.2, the cogirth of $M$ is at least $n.$ Suppose it is $n.$ Then there is a cocircuit $Q$ of $M$ with $Q=n.$ Let $Q^{\prime }=E\left(M\right)-Q.$ By Lemma 3.4, $Q^{\prime }$ is a hyperplane and so $r\left(Q^{\prime }\right)=r\left(M\right)-1.$ Again by Theorem 3.2, $r\left(Q\right)\ge n-1$ and $r\left(Q^{\prime }\right)\ge n-1.$ Therefore $r\left(Q\right)+r\left(Q^{\prime }\right)-r\left(M\right)=r\left(Q\right)-1.$ If $r\left(Q\right)=n-1,$ then $(Q,Q^{\prime })$ is a vertical $(n-1)$-separation of $M,$ a contradiction. Hence $r\left(Q\right)=n.$ Therefore, if $r\left(Q^{\prime }\right)\ge n,$ then $(Q,Q^{\prime })$ is a vertical $n$-separation of $M,$ again a contradiction. Consequently, $r\left(Q^{\prime }\right)=n-1.$ This implies that every $n$-element set in $M{Q}^{\prime }=M\setminus Q$ is a circuit. It follows that $M{Q}^{\prime }$ is isomorphic to the uniform matroid $U_{n-1,q},$ where $q=Q^{\prime }\ge n+1.$

If $n\ge 3,$ then $q\ge n+1\ge 4$ and so $M$ contains the uniform matroid $U_{2,4}$ as a minor, a contradiction to the fact that $M$ is binary. Hence $n=2.$ Therefore $M\setminus Q$ is isomorphic to $U_{1,q}.$ This implies that $M\setminus Q$ is the cycle matroid of the connected graph on two vertices and $q$ edges. It follows that $M=M\left(G\right)$, where $G$ is the graph obtained from a triangle by adjoining $q-1$ edges parallel to one of the edge. As $G$ contains a vertex of degree two, it is not 3-connected and so $M\left(G\right)$ is not vertically 3-connected. Therefore $M$ is not vertically $(n+1)$-connected, a contradiction. This completes the proof. □

Lemma 3.7

Let $n\ge 2$ be an integer and let $M$ be an $n$-connected, vertically $(n+1)$-connected binary matroid with $E\left(M\right)\ge 2n+1$ and girth at least $n+1.$ Then $M$ is $(n+1)$-connected.

Proof

Since $M$ is vertically $(n+1)$-connected, $k\left(M\right)\ge n+1.$ Also, the girth $g\left(M\right)$ of $M$ is at least $n+1.$ By Lemma 3.6, the cogirth of $M$ is also at least $n+1.$ Let $r$ be the rank of $M.$ Then $r+1\ge g\left(M\right)\ge n+1$ and therefore $r\ge n\ge 2.$ Suppose $M$ is isomorphic to the uniform matroid $U_{r,\mathrm{m}}$ for some $m$ with $m\ge 2r-1.$ Then $m>r.$ Suppose $m=r+1.$ Then $M$ is a circuit and hence the cogirth of $M$ is $2,$ a contradiction. Thus $m\ge r+2.$ This implies that $U_{r,\mathrm{m}}$ contains $U_{2,4}$ as a minor. Hence $U_{2,4}$ is a minor of the binary matroid $M,$ a contradiction. Therefore $M$ is not isomorphic to the uniform matroid $U_{r,\mathrm{m}}$ with $m\ge 2r-1.$ Now, by Theorem 3.1, $\lambda \left(M\right)=mink\left(M\right),g\left(M\right)\ge n+1.$ Hence $M$ is $(n+1)$-connected. □

4 Main results

In the following theorem, we provide some necessary conditions for the splitting matroid $M_T$ to be $n$-connected.

Theorem 4.1

Let $n\ge 2$ and $M$ be an $n$-connected and vertically $(n+1)$-connected binary matroid with $E\left(M\right)\ge 2n+1$ and $T\subset E\left(M\right)$ with $T=n.$ Suppose the splitting matroid $M_T$ is $n$-connected and $Q$ is a cocircuit of $M$ intersecting $T.$ Then

(i) $Q\ge max2Q\cap T,n+1;$

(ii) neither $T$ nor $Q\Delta T$ is an $n$-circuit in $M$ if $n$ is even.

Proof

By Theorem 3.2, every circuit of $M$ has size at least $n$ and, by Lemma 3.6, every cocircuit of $M$ has size at least $n+1.$ Similarly, every cocircuit of $M_T$ contains at least $n$ elements. As $T=n,$ $T$ does not contain any cocircuit of $M.$ By Lemma 2.4 (iii), $r^{\prime }\left(M_T\right)=r\left(M\right)+1.$

Suppose $Q$ is a cocircuit of $M$ containing $k>0$ elements of $T.$ If $T$ is a subset of $Q,$ then, by Theorem 2.2 (i), $Q-T$ is a cocircuit of the splitting matroid $M_T.$ Further, if $T$ is not a subset of $Q,$ then $Q\Delta T$ is a cocircuit of $M_T$ by Theorem 2.2 (iii). In both the cases, $Q\Delta T$ is a cocircuit of $M_T.$ Therefore, $n\le Q\Delta T=Q-T+T-Q=Q+T-2k=Q+n-2k$ giving $2k\le Q.$ Thus $Q\ge max2k,n+1.$ This proves (i).

We now prove (ii). Suppose $n$ is even. Assume that $Q\Delta T=C$ is an $n$-circuit of $M.$ In a binary matroid, intersection of a circuit and a cocircuit contains an even number of elements. Therefore $C\cap Q=Q-T$ is even. Consequently, $C\cap T=T-Q=n-Q-T$ is even as $n$ is even. Hence, by Lemma 2.3, $C$ is an $n$-circuit of $M_T.$ Already $C$ is an $n$-cocircuit of $M_T.$ This is a contradiction by Lemma 3.3. Assume that $T$ is an $n$-circuit of $M.$ Then, by Lemma 2.3, $T$ is also a circuit of $M_T.$ Further, by Definition 1.1, $T$ is a cocircuit of $M_T.$ This is a contradiction by Lemma 3.3. □

We now prove Theorem 1.4.

Proof of Theorem 1.4

By Theorem 3.2, the girth of $M$ is at least $n$ and, by Lemma 3.6, the cogirth of $M$ is at least $n+1.$ Hence $T$ does not a contain cocircuit of $M$ as $T=n.$ Therefore, by Lemma 2.4 (iii), $r^{\prime }\left(M_T\right)=r\left(M\right)+1.$ We prove the result by contradiction. Suppose $M_T$ is not $n$-connected. Then it has an $(n-1)$-separation $(A,B).$ Therefore $\text{min}A,B\ge n-1$ and $r^{\prime }\left(A\right)+r^{\prime }\left(B\right)-r^{\prime }\left(M_T\right)\le n-2.$Suppose $A=n-1.$ Then $A$ is independent in $M$ and so, by Lemma 2.3, $A$ is independent in $M_T$ also. Suppose $A$ contains a cocircuit $Q$ of $M_T.$ Then $Q\le A=n-1$ and hence, by Theorem 3.2, $Q$ is not a cocircuit of $M.$ By Theorem 2.2, $Q$ belongs to one of the three classes ${\mathcal{C}}_1^{\ast }$, ${\mathcal{C}}_3^{\ast }$ or ${\mathcal{C}}_4^{\ast }.$ Suppose $Q\in {\mathcal{C}}_1^{\ast }.$ Then $Q=C^{\ast }-T,$ where $C^{\ast }$ is a cocircuit of $M$ containing $T.$ Then, by hypothesis, $C^{\ast }\ge 2Q\cap T=2T=2n$ and so $Q\ge n,$ a contradiction. Suppose $Q\in {\mathcal{C}}_4^{\ast }.$ Then $Q=(C_1^{\ast }\cup C_2^{\ast }\cup \cdots \cup C_k^{\ast })-T,$ where $k\ge 2$ and $C_i^{\ast }$ are mutually disjoint cocircuits of $M$ and each of them contains at least one element of $T.$ Since $C_i^{\ast }\ge n+1$ and $T=n,$ we have $Q\ge (C_1^{\ast }\cup C_2^{\ast })-T\ge C_1^{\ast }+C_2^{\ast }-T\ge 2n+2-n=n+2>n-1\ge Q,$ a contradiction. Hence $Q\in {\mathcal{C}}_3^{\ast }.$ Therefore $Q=C^{\ast }\Delta T,$ where $C^{\ast }$ is a cocircuit of $M$ intersecting $T$ but not containing $T.$ Then $C^{\ast }\ge max2k,n+1,$ where $k=C^{\ast }\cap T.$ Hence $Q=C^{\ast }\Delta T=C^{\ast }+T-2C^{\ast }\cap T\ge 2k+n-2k=n>n-1\ge Q,$ a contradiction. Thus $A$ does not contain a cocircuit of $M_T.$

Hence $r^{\prime }\left(B\right)=r^{\prime }\left(M_T\right).$ This gives $n-1=r^{\prime }\left(A\right)=r^{\prime }\left(A\right)+r^{\prime }\left(B\right)-r^{\prime }\left(M_T\right)\le n-2,$ which is a contradiction. Similarly, we get a contradiction if $B=n-1.$

Therefore $A\ge n$ and $B\ge n.$ If $r\left(A\right)\ge n$ and $r\left(B\right)\ge n,$ then, $r\left(A\right)+r\left(B\right)-r\left(M\right)\le r^{\prime }\left(A\right)+r^{\prime }\left(B\right)-(r^{\prime }\left(M_T\right)-1)\le n-2+1=n-1$and so $(A,B)$ is a vertical $n$-separation of $M,$ a contradiction. Hence $r\left(A\right)=n-1$ or $r\left(B\right)=n-1.$ Without loss of generality assume that $r\left(A\right)=n-1.$ Therefore every subset of $A$ containing $n$ elements is dependent in $MA=M\setminus B$ and so in $M.$ This shows that every subset of $A$ of size $n$ is an $n$-circuit of $MA.$ If $A\ge n+1,$ then $U_{2,4}$ is a minor of the binary matroid $MA,$ which is a contradiction. Hence $A=n.$ Thus $A$ is an $n$-circuit of $M.$ By Lemma 3.6, $A$ does not contain a cocircuit of $M.$ This gives $r\left(B\right)=r\left(M\right).$

Now, if $r^{\prime }\left(B\right)=r\left(B\right)+1,$ then $r\left(A\right)+r\left(B\right)-r\left(M\right)\le r^{\prime }\left(A\right)+(r^{\prime }\left(B\right)-1)-(r^{\prime }\left(M_T\right)-1)=r^{\prime }\left(A\right)+r^{\prime }\left(B\right)-r^{\prime }\left(M_T\right)\le n-2.$This implies that $(A,B)$ is an $(n-1)$-separation of $M,$ a contradiction. Hence $r^{\prime }\left(B\right)=r\left(B\right).$ If $A$ does not contain a cocircuit of $M_T,$ then $r^{\prime }\left(M_T\right)=r^{\prime }\left(B\right)=r\left(B\right)=r\left(M\right),$ a contradiction to Lemma 2.4 (iii).

Thus $A$ contains a cocircuit $Q$ of $M_T.$ Therefore $Q\le A=n.$ As cogirth of $M$ is at least $n+1,$ $Q$ is not a cocircuit of $M.$ Further, $A\ne T$ as $T$ is not an $n$-circuit of $M.$ Therefore $Q\ne T.$ By Theorem 2.2, $Q\in {\mathcal{C}}_i^{\ast }$ for some $i\in 1,3,4.$ Suppose $Q\in {\mathcal{C}}_1^{\ast }.$ Then $Q=C^{\ast }-T$ for some cocircuit $C^{\ast }$ of $M$ containing $T.$ Therefore $C^{\ast }\ge 2C^{\ast }\cap T=2T=2n.$ Hence $Q=C^{\ast }-T\ge 2n-n=n.$ This implies that $Q=A.$ Since $A$ is an $n$-circuit, $C^{\ast }\Delta T$ is an $n$-circuit of $M,$ a contradiction to the assumption that $C^{\ast }\Delta T$ is not an $n$-circuit of $M$. Suppose $Q\in {\mathcal{C}}_3^{\ast }.$ Then $Q=C^{\ast }\Delta T$ for some cocircuit $C^{\ast }$ of $M$ intersecting $T$ but not containing $T.$ Then $C^{\ast }\ge 2C^{\ast }\cap T$ and so $Q=C^{\ast }\Delta T=C^{\ast }+T-2C^{\ast }\cap T\ge T=n.$ This gives $C^{\ast }\Delta T=Q=A.$ Hence $C^{\ast }\Delta T$ is an $n$-circuit of $M,$ a contradiction. Therefore $Q\in {\mathcal{C}}_4^{\ast }.$ Hence $Q=(C_1^{\ast }\cup C_2^{\ast }\cup \cdots \cup C_k^{\ast })-T,$ where $k\ge 2$ and $C_i^{\ast }$ are mutually disjoint cocircuits of $M$ and each of them contains at least one element of $T.$ Since $C_i^{\ast }\ge n+1$ and $T=n,$ we have $Q\ge (C_1^{\ast }\cup C_2^{\ast })-T\ge C_1^{\ast }+C_2^{\ast }-T\ge 2n+2-n=n+2>n\ge Q,$ a contradiction. □

We prove Theorem 1.5, which is restated here for convenience. In view of Lemma 3.7, the equivalence of statements (1) and (3) follows directly from Theorem 1.3. However, we provide a shorter proof of the same.

Theorem 4.2

Let $n\ge 2$ and $M$ be an $(n+1)$-connected binary matroid with $E\left(M\right)\ge 2n+1$ and $T\subset E\left(M\right)$ with $T=n.$ Then the following statements are equivalent.

(1)	The matroid $M_T$ is $n$-connected.

(2)	For every cocircuit $Q$ in $M$ intersecting $T,$ $Q\ge max2Q\cap T,n+1.$

(3)	For $A\subset E\left(M\right)$ with $A=n-1,$ there is a circuit $C$ in $M$ such that $C\cap T$ is odd and $C\cap A=\varphi .$

Proof

Since $M$ is an $(n+1)$-connected, it is $n$-connected as well as vertically $(n+1)$-connected. Further, by Theorem 3.2 every circuit and every circuit of $M$ contains at least $n+1$ elements. Therefore $T$ does not contain a cocircuit of $M$ as $T=n.$

(1) $\Rightarrow$ (2) follows from Theorem 4.1.

(2) $\Rightarrow$ (1) follows from Theorems 4.1 and 3.2.

(1) $\Rightarrow$ (3). Suppose $M_T$ is $n$-connected but (3) does not hold. Then there is a set $A\subset E\left(M\right)$ with $A=n-1$ such that $C\cap A\ne \varphi$ for every circuit $C$ in $M$ with $C\cap T$ an odd integer. Let $B=E\left(M\right)-A.$ Then $B\ge n+1$ and, by Lemma 2.4 (i), $r\left(B\right)=r^{\prime }\left(B\right).$ Since $A$ is not a circuit of $M,$ by Lemma 2.3, $A$ is independent in $M_T$ and so $r\left(A\right)=r^{\prime }\left(A\right).$ By Theorem 3.2, $A$ does not contain a cocircuit of $M.$ Therefore $r\left(B\right)=r\left(M\right)$ by Corollary 3.5. Hence $r^{\prime }\left(A\right)+r^{\prime }\left(B\right)-r^{\prime }\left(M_T\right)=r\left(A\right)+r\left(B\right)-r\left(M\right)-1=r\left(A\right)-1=n-2.$Thus $(A,B)$ is an $(n-1)$-separation of $M_T,$ a contradiction.

(3) $\Rightarrow$ (1). Assume that (3) holds but (1) does not hold. Then $M_T$ has an $(n-1)$-separation $(A,B).$ Therefore min$A,B\ge n-1$ and $r^{\prime }\left(A\right)+r^{\prime }\left(B\right)-r^{\prime }\left(M_T\right)\le n-2.$

Suppose $A\ge n$ and $B\ge n.$ By Lemma 2.4, $r\left(A\right)+r\left(B\right)-r\left(M\right)\le r^{\prime }\left(A\right)+r^{\prime }\left(B\right)-r^{\prime }\left(M_T\right)+1\le n-2+1\le n-1.$Hence $(A,B)$ is an $n$-separation of $M$, a contradiction to the fact that $M$ is $(n+1)$-connected.

Therefore we may assume that $A=n-1.$ By (3) and Lemma 2.4 (ii), $r^{\prime }\left(B\right)=r\left(B\right)+1.$ Consequently, $r\left(A\right)+r\left(B\right)-r\left(M\right)\le r^{\prime }\left(A\right)+r^{\prime }\left(B\right)-1-r^{\prime }\left(M_T\right)+1\le n-2.$This shows that $(A,B)$ is an $(n-1)$-separation of $M,$ a contradiction. □

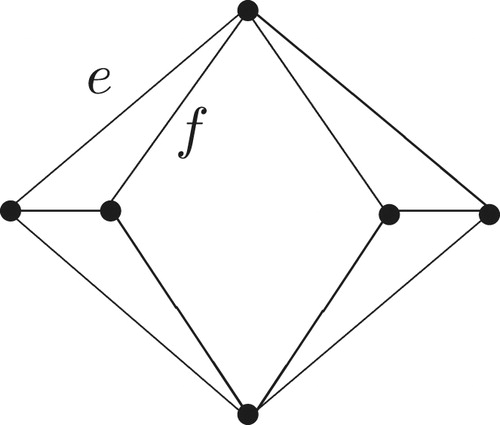
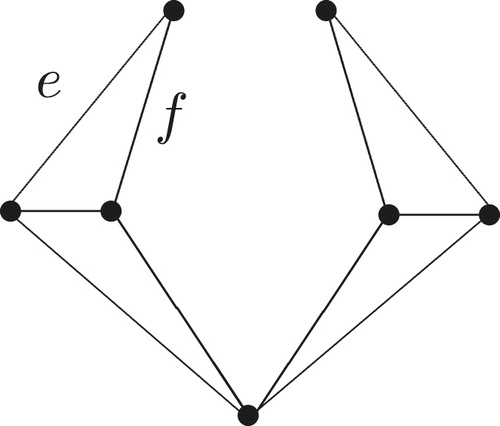
Remark 4.3

In the following example, we show that the condition on the matroid $M$ given in Theorem 1.4 that $M$ is vertically $(n+1)$-connected cannot be dropped. The graph $G$ of Fig. 1 (a) is 2-connected but not 3-connected. Hence its cycle matroid $M\left(G\right)$ is 2-connected but not vertically 3-connected. Let $T=e,f,$ where $e$ and $f$ are the edges of $G$ as shown in Fig. 1 (a). Then $T$ satisfies the hypothesis of Theorem 1.4. The graph $G_T$ obtained by splitting away the edges $e$ and $f$ is shown in Fig. 1 (b). Clearly, $M{\left(G\right)}_T=M\left(G_T\right).$ However, $M\left(G_T\right)$ is not 2-connected and so $M{\left(G\right)}_T$ is not 2-connected. (a) The graph $G$

Fig. 1 Splitting of a graph.

Notes

Peer review under responsibility of Kalasalingam University.