Domination in graphoidally covered graphs: Least-kernel graphoidal graphs-II

Peer review under responsibility of Kalasalingam University.

Abstract

Given a graph $G=(V,E)$, not necessarily finite, a graphoidal cover of $G$ means a collection $\Psi$ of non-trivial paths in $G$ called $\Psi$-edges, which are not necessarily open (not necessarily finite), such that every vertex of $G$ is an internal vertex of at most one path in $\Psi$ and every edge of G is in exactly one path in $\Psi$. The set of all graphoidal covers of a graph $G=(V,E)$ is denoted by ${\mathcal{G}}_G$ and for a given $\Psi \in {\mathcal{G}}_G$ the ordered pair $(G,\Psi )$ is called a graphoidally covered graph.

Two vertices $u$ and $v$ of $G$ are $\Psi$-adjacent if they are the ends of an open $\Psi$-edge. A set $D$ of vertices in $(G,\Psi )$ is $\Psi$-independent if no two vertices in $D$ are $\Psi$-adjacent and is said to be $\Psi$-dominating if every vertex of $G$ is either in $D$ or is $\Psi$-adjacent to a vertex in $D$; $G$ is ${\gamma }_{\Psi }\left(G\right)$-definable (${\gamma }_{i\Psi }\left(G\right)$-definable) if $(G,\Psi )$ has a finite $\Psi$-dominating ($\Psi$-independent $\Psi$-dominating) set. Clearly, if $G$ is ${\gamma }_{i\Psi }\left(G\right)$-definable, then $G$ is ${\gamma }_{\Psi }\left(G\right)$-definable and ${\gamma }_{\Psi }\left(G\right)\le {\gamma }_{i\Psi }\left(G\right)$. Further if for any graphoidal cover $\Psi$ of $G$ such that ${\gamma }_{\Psi }\left(G\right)={\gamma }_{i\Psi }\left(G\right)$ then we call $\Psi$ as a least-kernel graphoidal cover of $G$ (in short, an LKG cover of $G$). A graph is said to be a least kernel graphoidal graph or simply an LKG graph if it possesses an LKG cover.

This paper is based on a conjecture by Dr. B.D Acharya, “Every graph possesses an LKG cover”. After finding an example of a graph which does not possess an LKG cover, we obtain a necessary condition in the form of forbidden subgraph for a graph to be a least kernel graphoidal graph. We further prove that the condition is sufficient for a block graph with a unique nontrivial block. Thereafter we identify certain classes of graphs in which every graph possesses an LKG cover. Moreover, following our surmise that every graph with $\Delta \le 6$ possesses an LKG cover, we were able to show that every finite graph with $\Delta \le 3$ is indeed an LKG graph.

Keywords:

• Domination
• Graphoidal cover
• Least-kernel graphoidal cover

1 Introduction

Throughout this paper we consider simple graphs without loops as treated in most of the standard text-books on graph theory such as [1]. For terminologies used in this paper without defining explicitly we refer to [2]. Further, unless mentioned otherwise, graphs will be assumed to be connected and infinite.

The concept of graphoidal covers [3] was first introduced by Acharya and Sampathkumar in 1987 as a close variant of another emerging discrete structure called semigraphs [4]. Many interesting notions like graphoidal covering number [3], graphoidal labeling [5], graphoidal signed graphs [6], etc. were introduced and are being studied extensively. In particular, notion of graphoidal covering number of a graph has attracted many researchers and numerous work is present in literature [7–11^{[7][8][9][10][11]}]. Acharya and Gupta in 1999 extended the concept of graphoidal covers to infinite graphs and introduced notion of domination in graphoidally covered graphs [2,12,13]. A detailed treatment of graphoidal covers and graphoidally covered graphs is given in [2,14].

In this paper we continue our work in [15] and hence extend the work on domination in graphoidally covered graph [2,12,13]. A graphoidally covered graph $(G,\Psi )$ consists of a graph $G=(V,E)$ and a collection $\Psi$ of nontrivial paths in $G$, which are not necessarily open (not necessarily finite), such that

[G1]	=	every vertex of $G$ is an internal vertex of at most one path in $\Psi$ and
[G2]	=	every edge of $G$ is in exactly one path in $\Psi$.

The set $\Psi$ is called a graphoidal cover of the graph $G$ and a member of $\Psi$ is called a $\Psi$-edge. The set of all graphoidal covers of $G$ is denoted by ${\mathcal{G}}_G$.

It may be noted that a $\Psi$-edge could possibly be infinite; in particular, it may be a one-way infinite path (or, the often so-called ‘ray’) or a two-way infinite path. Further, a finite open $\Psi$-edge has two distinct end vertices and a closed $\Psi$-edge has only one end vertex, which is specified by $\Psi$. Next, a one-way infinite $\Psi$-edge has exactly one end vertex while a two-way infinite $\Psi$-edge has no end vertex. Moreover three types of vertices may exist in a graphoidally covered graph $(G,\Psi ),$ viz. exterior vertex or a black vertex (vertex which is not an internal vertex of any $\Psi$-edge), interior vertex or a white vertex (vertex which is not an end-vertex of any $\Psi$-edge) and composite vertex (vertex which is neither an exterior vertex nor an interior vertex). In the diagrammatic representation, black vertex is shown as a small filled circle, white vertex is shown as a small unfilled circle and a composite vertex is represented as an unfilled circle with as many small tangents to the circle as the number of $\Psi$-edges for which this vertex is the end-vertex and each tangent indicates an end-vertex of the corresponding $\Psi$-edge.

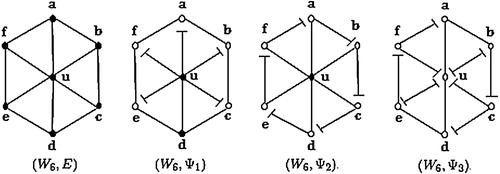
In Fig. 1 we give diagrammatic representation of four different graphoidal covers, namely, $E,{\Psi }_1,{\Psi }_2$ and ${\Psi }_3$ of wheel $W_6$, where $E$ is the edge set of $W_6$, ${\Psi }_1=\{(u,a),(u,b),(u,c),(u,d),(u,e),(u,f),(d,e,f,a,b,c,d)\}$ ${\Psi }_2=\{(u,a,b),(u,b,c),(u,c,d),(u,d,e),(u,e,f),(u,f,a)\}$ ${\Psi }_3=\{(f,e,d,u,a,b,c),(u,f,a),(u,c,d),(u,e),(u,b)\}.$

Fig. 1 A graphoidally covered graph.

Clearly, $E\in {\mathcal{G}}_G$ and hence we call $E≕E\left(G\right)$, the edge set of $G$, the trivial graphoidal cover of $G$; a graphoidal cover that is not trivial will be referred to as being nontrivial. Two distinct vertices $u$ and $v$ of $G$ are $\Psi$-adjacent if they are the ends of an open $\Psi$-edge; a vertex is said to be self $\Psi$-adjacent if it is both the ‘initial’ and the ‘terminal’ end of a closed $\Psi$-edge (i.e., a cycle in $\Psi$) — in either case, we represent the fact by writing $u\Psi v$. The $\Psi$-degree $d_{\Psi }\left(u\right)$ of a vertex $u$ is then defined as the number of $\Psi$-edges having $u$ as their end-vertex. A vertex is said to be a $\Psi$-pendant vertex if its $\Psi$-degree is one and a vertex is said to be a $\Psi$-support if it is $\Psi$-adjacent to at least one $\Psi$-pendant vertex.

A theoretical motivation to study graphoidally covered graphs is that every ear-decomposition of a finite $2$-connected ($2$-edge connected) graph $G$ (cf.: [1], p.146) is a graphoidal cover of $G$, but not conversely; thus, the notion of a graphoidal cover of any graph can be looked upon as a generalization of the notion of an ear-decomposition.

A set $D$ of vertices in a graphoidally covered graph $(G,\Psi )$ is a $\Psi$-dominating set (or ‘$\Psi$-domset’ for short) if every vertex of $G$ is either in $D$ or is $\Psi$-adjacent to a vertex in $D$; if $(G,\Psi )$ contains a finite $\Psi$-dominating set, then the least cardinality of such a set is denoted by ${\gamma }_{\Psi }\left(G\right)$ and is called the $\Psi$-domination number of $(G,\Psi )$ ; such graphs are called ${\gamma }_{\Psi }$-definable.

A set $D$ of vertices in a graphoidally covered graph $(G,\Psi )$ is a $\Psi$-independent set if no pair of distinct vertices in $D$ are $\Psi$-adjacent and a $\Psi$-dominating set $D$, which is also $\Psi$-independent is called a $\Psi$-kernel. If $(G,\Psi )$ contains a finite $\Psi$-kernel then the least cardinality of a $\Psi$-kernel of $(G,\Psi )$ is denoted by ${\gamma }_{i\Psi }\left(G\right)$ and then $G$ is said to be ‘${\gamma }_{i\Psi }\left(G\right)$-definable’. In case $(G,\Psi )$ is ${\gamma }_{\Psi }\left(G\right)$- (${\gamma }_{i\Psi }\left(G\right)$-) definable then it is often convenient to call a $\Psi$-dominating set ($\Psi$-kernel) consisting of ${\gamma }_{\Psi }\left(G\right)$ (${\gamma }_{i\Psi }\left(G\right)$) vertices a ${\gamma }_{\Psi }\left(G\right)$-set (${\gamma }_{i\Psi }\left(G\right)$-set). 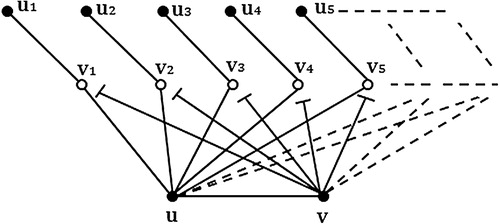Clearly, if $(G,\Psi )$ is ${\gamma }_{i\Psi }\left(G\right)$-definable then it is ${\gamma }_{\Psi }\left(G\right)$-definable, but the converse may not be true for infinite graphs. In Fig. 2, we have an infinite graph $G$ and a graphoidal cover $\Psi$ of $G$ such that $G$ is ${\gamma }_{\Psi }\left(G\right)$-definable but not ${\gamma }_{i\Psi }\left(G\right)$-definable. However, if $G$ is an infinite claw free graph, then for the trivial graphoidal cover $\Psi =E$, ${\gamma }_{\Psi }\left(G\right)$-definability implies ${\gamma }_{i\Psi }\left(G\right)$-definability and in that case ${\gamma }_{\Psi }\left(G\right)={\gamma }_{i\Psi }\left(G\right)$. This fact can be proved using the technique used in the proof of Allan–Laskar Theorem [16] on claw free graphs.

Fig. 2 $(G,\Psi )$, where $\Psi =\left\{(u,v)\right\}\cup \{(u,v_i,u_i):i\in \mathbb{N}\}\cup \{(v,v_i):i\in \mathbb{N}\}$, is ${\gamma }_{\Psi }\left(G\right)$-definable but not ${\gamma }_{i\Psi }\left(G\right)$-definable and ${\gamma }_{\Psi }\left(G\right)=\{u,v\}$.

Theorem 1.1

If $G$ is a $\gamma$-definable infinite claw free graph, then $G$ is ${\gamma }_i$-definable and $\gamma \left(G\right)={\gamma }_i\left(G\right)$.

For $\Psi =E\left(G\right)$ we denote ${\gamma }_{E\left(G\right)}\left(G\right)≕\gamma \left(G\right),$ and call it the domination number of $G$, and denote ${\gamma }_{iE\left(G\right)}\left(G\right)≕{\gamma }_i\left(G\right)$, and call it the independent domination number of $G$, subject to the existence of these parameters, well in compatibility with these notations in the theory of domination in the case of finite graphs (e.g., see [17–19^[17][18][19]]).

2 Least kernel graphoidal graphs

A graphoidal cover $\Psi$ of graph $G$ is such that $G$ is ${\gamma }_{i\Psi }\left(G\right)$-definable then (2.1) ${\gamma }_{\Psi }\left(G\right)\le {\gamma }_{i\Psi }\left(G\right).$(2.1) For the trivial graphoidal cover $\Psi =E$, the above inequality reduces to ${\gamma }_E\left(G\right)\le {\gamma }_{iE}\left(G\right)i.e.,\gamma \left(G\right)\le {\gamma }_i\left(G\right).$We call a graphoidal cover $\Psi \in {\mathcal{G}}_G$ to be a least kernel graphoidal cover (or simply an LKG cover) of $G$ if $G$ is ${\gamma }_{i\Psi }\left(G\right)$-definable and (2.2) ${\gamma }_{\Psi }\left(G\right)={\gamma }_{i\Psi }\left(G\right).$(2.2) A graph $G$ is said to be a least kernel graphoidal graph (or simply, LKG graph) if $G$ possesses an LKG cover.

For $\Psi =E\left(G\right)$, this reduces to the well known equality $\gamma \left(G\right)={\gamma }_i\left(G\right),$ first considered by Allan–Laskar. By Allan Laskar Theorem [16], for every finite claw free graph $\gamma \left(G\right)={\gamma }_i\left(G\right)$. Also, for every $\gamma$-definable infinite claw free graph $\gamma \left(G\right)={\gamma }_i\left(G\right)$. Therefore the trivial graphoidal cover of every finite claw free graph and every $\gamma$-definable infinite claw free graph is an LKG cover.

Following are some of the basic but important observations which arise from the definition of graphoidal cover and an LKG cover.

Lemma 2.1

[15]

Every pendant vertex of a graph $G$ is a $\Psi$-pendant vertex, for each $\Psi \in {\mathcal{G}}_G$.

Lemma 2.2

[15]

If $u\in V\left(G\right)$ is a support to $n(\ge 3)$ pendant vertices, then for each $\Psi \in {\mathcal{G}}_G$, at least $(n-2)$ of these pendant vertices are $\Psi$-pendant vertices, with $u$ as their common $\Psi$-support.

Lemma 2.3

[15]

Let $\Psi \in {\mathcal{G}}_G$ be such that $G$ is ${\gamma }_{i\Psi }\left(G\right)$-definable and if $u\in V\left(G\right)$ is a $\Psi$-support to more than one $\Psi$-pendant vertices, then every ${\gamma }_{\Psi }\left(G\right)$-set of $G$ contains $u$.

Lemma 2.4

[15]

If $\Psi \in {\mathcal{G}}_G$ is an LKG cover of $G$ and $u,v\in V\left(G\right)$ are such that $u\Psi v$, then at most one of $u$ and $v$ can be a $\Psi$-support to more than one $\Psi$-pendant vertex.

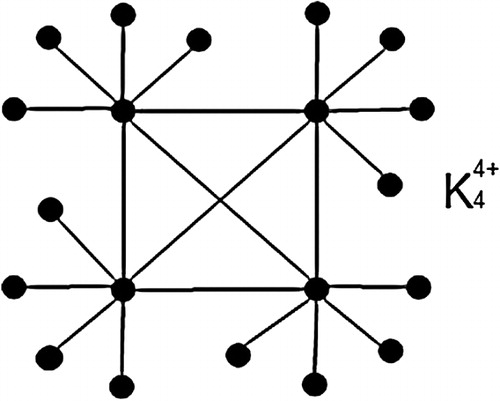
The contents of this paper are based on a conjecture by Dr. B.D Acharya “Does every graph possess a least kernel graphoidal cover ?” In [15], it is proved that the graph $K_4^{4+}$ (see Fig. 3) obtained by adjoining $4$ new vertices of degree one at each vertex of complete graph $K_4$ is not an LKG graph. Thus not every graph is an LKG graph. Hence it becomes interesting to find those graphs which possesses an LKG cover.

Fig. 3 Example of a graph which is not an LKG graph.

Before going into the exploration of LKG graphs, we shall first show that any graph having $K_4^{4+}$ as its subgraph such that pendant vertices of $K_4^{4+}$ are pendant vertices in the graph is not an LKG graph.

Theorem 2.5

If $G$ is a graph having $K_4^{4+}$ as its subgraph such that pendant vertices of $K_4^{4+}$ are pendant vertices in $G$. Then $G$ is not an LKG graph.

Proof

Let $\Psi$ be any graphoidal cover of $G$. If $G$ is not ${\gamma }_{\Psi }$-definable, then by definition, $\Psi$ cannot be an LKG cover. Let $\Psi$ be such that $G$ is ${\gamma }_{\Psi }$-definable. We shall prove that $\Psi$ is not an LKG cover. In view of Lemma 2.4, it is enough to show that there exists a pair of $\Psi$-adjacent vertices in $(G,\Psi )$ such that each is $\Psi$-support to two $\Psi$-pendant vertices. Further, since every vertex in $K_4^{4+}$ is a support to $4$ pendants, by Lemma 2.2, every vertex in $K_4^{4+}$ is $\Psi$-adjacent to at least two $\Psi$-pendant vertices. Hence it suffices to show that there exists a pair of $\Psi$-adjacent vertices in $V\left(K_4\right)$ i.e., there exists an open $\Psi$-edge $P$ in $\Psi$ having both its end vertex in $K_4$.

Suppose on the contrary, graphoidal cover $\Psi$ be such that for each $P\in \Psi$, either $P$ is closed or at most one end vertex of $P$ lies on $K_4$. Let $V\left(K_4\right)=\{w,x,y,z\}$ and $Q$ be a $\Psi$-edge such that $Q$ contains maximum number of edges of $E\left(K_4\right)$ i.e., $|E\left(R\right)\cap E\left(K_4\right)|\le |E\left(Q\right)\cap E\left(K_4\right)|$ for all $R\in \Psi$. Then by definition of graphoidal cover, $1\le |E\left(Q\right)\cap E\left(K_4\right)|\le 4$ and thus we have four possibilities:

Case 1. $|E\left(Q\right)\cap E\left(K_4\right)|=4$.

Then $Q$ is a cycle of length $4$ and in that case one of the diagonal of the cycle must be a $\Psi$-edge, a contradiction to the assumption that at most one end vertex of an open $\Psi$-edge lies on $K_4$.

Case 2. $|E\left(Q\right)\cap E\left(K_4\right)|=3$.

If $E\left(P\right)⊈E\left(K_4\right)$, then as $Q$ contains three edges of $K_4$, at least three vertices say $x,y,z$ of $K_4$ are internal vertices of $Q$. Hence one of the edges $xy,yz,zx$ must be a $\Psi$-edge, contradiction. Thus $E\left(Q\right)\subseteq E\left(K_4\right)$ and consequently, $Q$ must be a cycle of length $3$. Without loss of generality, assume that $Q=(w,x,y,w)$. Let $Q_z$ be the $\Psi$-edge containing the edge $yz$. Clearly, $Q_z\ne (y,z)$. Since $y$ is an internal vertex of $Q$, it is an end vertex of $Q_z$ and hence $z$ is an internal vertex of $Q_z$. Also, $xz$ does not lie on $Q_z$ (for if, $Q_z$ contains $xz$, then $Q_z=(y,z,x)$, a contradiction). But then $xz$ is a $\Psi$-edge, again a contradiction.

Case 3. $|E\left(Q\right)\cap E\left(K_4\right)|=2$.

If $E\left(Q\right)\subseteq E\left(K_4\right)$, then $Q$ is an open path of length $2$ having both its end vertices in $V\left(K_4\right)$, a contradiction. Hence $E\left(Q\right)⊈E\left(K_4\right)$ and consequently, at least two vertices in $V\left(K_4\right)$ are internal vertices of $Q$. Without loss of generality, assume that $x,y$ are internal vertices of $Q$. If $xy\notin E\left(Q\right)$, then $xy$ is a $\Psi$-edge, contradiction. Hence $xy\in E\left(Q\right)$. Again without loss of generality, assume that $E\left(Q\right)\cap E\left(K_4\right)=\{wx,xy\}$. Let $Q_z$ be the $\Psi$-edge containing the edge $yz$. Then $y$ is an end vertex of $Q_z$, $z$ is an internal vertex of $Q_z$ and $xz$ does not lie on $Q_z$. But then $xz$ is a $\Psi$-edge, contradiction.

Case 4. $|E\left(Q\right)\cap E\left(K_4\right)|=1$.

Then by maximality of $Q$, any $\Psi$-edge can contain at most one edge of $E\left(K_4\right)$. Let $Q_w$, $Q_y$ and $Q_z$ be the $\Psi$-edges containing the edges $xw$, $xy$ and $xz$ respectively. Since $x$ can be an internal vertex to at most one $\Psi$-edge, with no loss of generality, we assume that $x$ is an end vertex of $Q_y$ and $Q_z$. But then $y$ and $z$ are internal vertices of $Q_y$ and $Q_z$ respectively and therefore $yz$ must be a $\Psi$-edge, a contradiction.

Thus in all the cases we arrived at a contradiction. Hence our assumption is wrong and there exists a pair of $\Psi$-adjacent vertices in $V\left(K_4\right)$. Thus $\Psi$ is not an LKG cover. Since $\Psi$ is arbitrary, we conclude that $G$ does not possess any LKG cover. Hence $G$ is not an LKG graph.  □

Thus Theorem 2.5 provides us with a necessary condition in the form of forbidden subgraph for a graph to be an LKG graph. Our hunch is that the condition of Theorem 2.5 is sufficient as well for a graph to be an LKG graph. In fact we shall prove that the condition is indeed sufficient in case of separable graphs with unique non-trivial block isomorphic to $K_n$ for some $n$.

Before that we need to discuss an important technique of decomposing trees into spiders which is used in [15] to obtain an LKG cover for any given tree. By spider we mean a tree $T$ homeomorphic to star $K_{1,n}$ for some positive integer $n$. The center of $K_{1,n}$ is called the root, and the paths having the root as one of their ends and the other ends being the pendant vertices of $T$ being called legs of the spider.

Algorithm

Spider Decomposition of a Tree $T(\ncong P_1)$

Set $k=0$, $F_0=T$ and $J=V\left(T\right)$.

STEP 1.	=	Choose any vertex $u_k$ in $V\left(F_k\right)\cap J$ of degree at least $1$ and maximal spider $S_k$ with $u_k$ as its root and the ends of its legs being the pendant vertices of $F_k$, ‘maximal’ in the sense that no other spider rooted at $u_k$ can have more number of legs than $S_k$. GO TO STEP 2.
STEP 2.	=	Set $F_{k+1}=F_k\setminus E\left(S_k\right)$ (the spanning forest obtained by deleting all the edges of $S_k$) and $J=V\left(S_k\right)$. GO TO STEP 3.
STEP 3.	=	Set $k≔k+1$. GO TO STEP 4.
STEP 4.	=	IF $\Delta \left(F_k\right)=0$, STOP, otherwise GO TO STEP 1.

Suppose this process terminates after repeating $n+1$ times, then we obtain a sequence of maximal spiders $S_0,S_1,\dots ,S_n$ in such a way that (i) the root $u_i$ of the $i$th spider $S_i$ lies on a leg of any one of the spiders $S_0,S_1,\dots ,S_{i-1}$, (ii) ${\bigcup }_{i=1}^{n}E\left(S_i\right)=E\left(T\right)$, and (iii) $E\left(S_i\right)\cap E\left(S_j\right)=\varnothing$ for all $i,j\in \{1,2,\dots ,n\},i\ne j$.

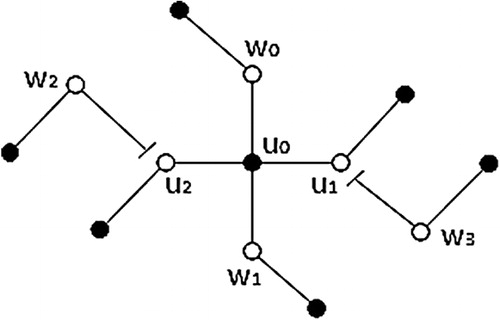
Let $\Psi$ consist of all the legs of all the spiders $S_0,S_1,\dots ,S_n$ and $D$ be the set consisting of all the roots $u_0,u_1,\dots ,u_n$ and all the vertices of degree at least $2$ of $T$. Then it was proved in [15] that $\Psi$ is an LKG cover of $T$ with $D$ as a ${\gamma }_{\Psi }\left(T\right)$(${\gamma }_{i\Psi }\left(T\right)$)-set (see Fig. 4).

Fig. 4 An LKG cover $\Psi$ of $T$ obtained by spider decomposition with initial root $u_0$. Here $D=\{u_0,u_1,u_2,w_0,w_1,w_2,w_3\}$ is a ${\gamma }_{\Psi }\left(T\right)\left({\gamma }_{i\Psi }\left(T\right)\right)$-set.

Theorem 2.6

[15]

Every finite tree $T$ admits a least-kernel graphoidal cover.

The technique of spider decomposition can be easily extended to show that every cactus possess an LKG cover.

Lemma 2.7

Let $G$ be a unicyclic graph with unique cycle $C$ and $v_C\in V\left(C\right)$. There exists an LKG cover $\Psi$ of $G$ with $v_C$ as one of its black vertices.

Proof

Let $V\left(C\right)=\{v_1(=v_C),\dots ,v_n\}$ and $T_1,\dots ,T_k$ be non-trivial components of the forest $G^{\prime }=G\setminus E\left(C_n\right)$. For each $j=1,\dots ,k$, let $V\left(T_j\right)\cap V\left(C\right)=\left\{v_{i_j}\right\}$. Let ${\Psi }_j$ be an LKG cover of $T_j$ obtained by spider decomposition technique taking $v_{i_j}$ as the initial root and $D_j$ be the corresponding ${\gamma }_{{\Psi }_j}$(${\gamma }_{j{\Psi }_j}$)-set. Consider the collection $\Psi ={\cup }_{j=1}^r{\Psi }_j\cup \left\{C\right\}$where $C$ is a closed path in $\Psi$ with $v_C$ as coincident end vertex. Then $\Psi$ is a graphoidal of $G$ with $v_C$ as one of its black vertex and the set $D={\cup }_{j=1}^r{D}_j\cup V\left(C\right)$ is a ${\gamma }_{\Psi }\left({\gamma }_{i\Psi }\right)$-set of $G$. Therefore $\Psi$ of $G$ is an LKG cover of $G$ and $G$ is an LKG graph.  □

Thus given any vertex of the cycle in the unicyclic graph, we can always construct an LKG cover with that vertex as one of the black vertex. This observation helps us in constructing an LKG cover for any given cactus. The concept of free paths in a graph will also be used while constructing an LKG cover for a cactus. A free path [2] in a graph $G$ is a maximal path each edge of which is a bridge in $G$. The set of all free paths of $G$ is denoted by $\mathcal{F}\left(G\right)$. The set of all free paths of the cactus $G$ in Fig. 5 is given by $\mathcal{F}\left(G\right)=\{(a,m,n),(a,m,o),(d,p),(g,c,q,r,s),(g,c,q,r,t),(k,i,j),(h,l)\}.$

Fig. 5 A cactus.

Theorem 2.8

Every finite cactus admits a least kernel graphoidal cover.

Proof

Let $G$ be a cactus having $n$ nontrivial blocks.

Claim

Corresponding to any vertex $v_B$ of any non-trivial block $B$ of $G$, there exists an LKG cover of $G$ with $v_B$ as one of its black vertex.

We will prove the claim by induction on $n$. If $n=1$, then $G$ is a unicyclic graph, whence by Lemma 2.7 we have the existence of the required LKG cover of $G$. Suppose the claim is true for $n\le k$. We now prove it for $n=k+1$. Let $B$ be any nontrivial block of $G$ and $v_B$ be any vertex of $B$. Let ${\mathcal{F}}_B=\{P\in \mathcal{F}\left(G\right):V\left(P\right)\cap V\left(B\right)\ne \varnothing \}$ and $S=V\left(B\right)\cup \left({\cup }_{P\in {\mathcal{F}}_B}V\left(P\right)\right).$Then $〈S〉$ is a unicyclic graph and therefore by Lemma 2.7 there exists an LKG cover ${\Psi }_S$ of $〈S〉$ with $v_B$ as one of its black vertex.

Let $G_1$ be the graph obtained from $G-E\left(〈S〉\right)$ by removing all the isolate vertices and $H_1,H_2,\dots ,H_m$ be the components of $G_1$. For each $i=1,2,\dots ,m$, let $V\left(H_i\right)\cap S=\left\{v_i\right\}$. Since each $H_i$ has at most $k$ nontrivial blocks, by induction hypothesis there exists an LKG cover ${\Psi }_i$ of $H_i$ such that $v_i$ is a black vertex of ${\Psi }_i$. Then clearly, $\Psi ={\cup }_{i=1}^m{\Psi }_i\cup {\Psi }_S$ is an LKG cover of $G$ with $v_B$ as one of its black vertex. Hence the proof of the claim follows by induction.  □

Next following our hunch that every graph with $\Delta \le 6$ admits an LKG cover, we were able to prove that every graph with $\Delta \le 3$ is indeed an LKG graph using a well known fact that a $2$-connected graph has an ear decomposition (cf. [1], p.146).

Theorem 2.9

Every finite graph $G$ with $\Delta \le 3$ admits an LKG cover.

Proof

We will prove this theorem in two cases:

CASE 1. $G$ is a nonseparable (2-connected) graph.

$G$ has an ear decomposition and therefore $E\left(G\right)$ can be partitioned into $P_0,P_1,\dots ,P_k$ such that $C=P_0$ is a cycle and $P_i$ for $i\ge 1$ is a path addition to the graph formed by $P_0,P_1,\dots ,P_{i-1}$. We claim that the graphoidal cover $\Psi =\{P_0,\dots ,P_k\}$ of $G$ is an LKG cover. For each $i=1,2..,k$, let $x_i,y_i$ be end vertices of the $\Psi$-edge $P_i$. Then the set $D=V\setminus \{y_0,\dots ,y_{k-1}\}$ is a ${\gamma }_{\Psi }\left({\gamma }_{i\Psi }\right)$-set of $(G,\Psi )$. Hence $G$ admits an LKG cover.

CASE 2. $G$ is a separable graph.

Let $B_1,\dots ,B_k$ be non-trivial blocks of $G$. For each $i=1,\dots ,k$, the block $B_i$ is 2-connected and hence as in Case 1, using ear decomposition of $B_i$, we obtain an LKG cover ${\Psi }_i$ of $B_i$ with $D_i$ as a ${\gamma }_{{\Psi }_i}\left({\gamma }_{i{\Psi }_i}\right)$-set of $B_i$.

Let $G^{\prime }$ be the forest obtained from $G\setminus \left({\cup }_{i=1}^{k}E\left(B_i\right)\right)$ by removing all isolates. Let $T_1,T_2,\dots ,T_m$ be the components of $G^{\prime }$. Then for each $i=1,2,\dots ,m$, the spider decomposition of $T_i$ provides us an LKG cover ${\Phi }_i$ of $T_i$ with a ${\gamma }_{{\Phi }_i}\left({\gamma }_{i{\Phi }_i}\right)$-set $D_i^{\prime }$. Let $\Psi =\left({\cup }_{i=1}^k{\Psi }_k\right)\cup \left({\cup }_{j=1}^m{\Phi }_j\right)\text{and}$ $D=\left({\cup }_{i=1}^k{H}_k\right)\cup \left({\cup }_{j=1}^m{D}_j^{\prime }\right)$ where $H_i=D_i\setminus V\left(G^{\prime }\right)$. Since $\Delta \le 3$, the collection $\Psi$ forms an LKG cover of $G$ with $D$ as ${\gamma }_{\Psi }\left({\gamma }_{i\Psi }\right)$-set. Thus $G$ admits an LKG cover.  □

Further following our surmise that the condition in Theorem 2.5 is sufficient also for a graph to be an LKG graph, we were able to prove that it is indeed sufficient for separable graphs with a unique non-trivial block isomorphic to $K_n$ for some $n$.

Theorem 2.10

Let $G$ be a finite separable graph with a unique non-trivial block $B\cong K_n$ for some $n$. Then $G$ is an LKG graph if and only if at most three vertices of $B$ are support to more than three pendant vertices in $G$.

Proof

Necessity follows from Theorem 2.5.

Conversely, Suppose $G$ has a unique non-trivial block (say) $B$ such that at most three vertices of $B$ could support more than three pendant vertices. Let $\{V_0,V_1,V_2,V_3,V_4\}$ be a partition of $V\left(B\right)$, where $V_i=\{w\in V\left(B\right):w\text{support}i\text{pendant vertices}\}(0\le i\le 3)$ $V_4=\{w\in V\left(B\right):w\text{support at least}4\text{pendant vertices}\}.$ For each $w\in V_3$, let the three pendant vertices with $w$ as their support be denoted by $x_w,y_w$ and $z_w$. For each $w\in V_2$, let $x_w,y_w$ denote the pendant vertices with $w$ as their support. For each $w\in V_1$, let $x_w$ be the unique pendant vertex with support $w$.

By hypothesis, $0\le \left|V_4\right|\le 3$, therefore we have two possibilities:

Case 1. $\left|V_4\right|\le 1$

Let $w_0$ be a vertex in $V\left(B\right)$ supporting maximum number of pendant vertices (in case there is no support in $B$, then we can take $w_0$ to be any vertex of $V\left(B\right)$). Let $H$ be the forest obtained from $G\setminus \left(V\left(B\right)\setminus \left\{w_0\right\}\right)$ by deleting all the isolate vertices. Let $T_1,T_2,\dots ,T_k$ be the components of $H$. For each $i(1\le i\le k)$, let $V\left(T_i\right)\cap N\left[B\right]=\left\{x_i\right\}$. By using spider decomposition technique keeping $x_i$ as the initial root, we get an LKG cover ${\Psi }_i$ of $T_i$ and a ${\gamma }_{{\Psi }_i}\left(T_i\right)\left({\gamma }_{i{\Psi }_i}\left(T_i\right)\right)$-set $D_i$.

Let ${\Phi }_1={\cup }_{i=0}^k{\Psi }_i$ and ${\Phi }_2=\left\{x_{w}w{y}_w:w\in V_2\cup V_3\setminus \left\{w_0\right\}\right\}$. Let $E^{\ast }\left(G\right)$ denote the set consisting of all edges in $G$ which are neither covered by ${\Phi }_1$ nor by ${\Phi }_2$. Then $\Phi ={\Phi }_1\cup {\Phi }_2\cup E^{\ast }\left(G\right)$ is an LKG cover of $G$ with ${\gamma }_{\Phi }\left(G\right)$-set (${\gamma }_{i\Phi }\left(G\right)$-set) $D={\cup }_{i=0}^k{D}_i\cup \left\{w_0\right\}\cup H_1\cup H_2$ where, $H_1=\{x_w:w\in V_1\cup V_2\cup V_3\setminus \left\{w_0\right\}\}$ $H_2=\{z_w:w\in V_3\setminus \left\{w_0\right\}\}.$

Case 2. $2\le \left|V_4\right|\le 3$

Choose any cycle $C$ in $B$ of length $3$ such that $V_4\subseteq V\left(C\right)$. Consider the forest $H$ obtained from $G\setminus (V\left(B\right)\setminus V\left(C\right))$ by removing all the edges of the cycle and the resulting isolates. Let $T_1,T_2,\dots ,T_r$ be components of $H$. Now for each $i(1\le i\le r)$, let $V\left(T_i\right)\cap N\left[B\right]=\left\{x_i\right\}$. Then with spider decomposition technique construct an LKG cover ${\Psi }_i$ of tree $T_i$ with $x_i$ as the initial root. Let $D_i$ be the ${\gamma }_{i{\Psi }_i}\left(T_i\right)$-set obtained during the process.

Let ${\Phi }_1={\cup }_{i=1}^k{\Psi }_i\cup \left\{C\right\}$ and ${\Phi }_2=\{x_{w}w{y}_w:w\in (V_2\cup V_3)\setminus V\left(C\right)\}$. Let $E^{\ast }\left(G\right)$ denote the set consisting of all edges in $G$ which are neither covered by ${\Phi }_1$ nor by ${\Phi }_2$. Then $\Phi ={\Phi }_1\cup {\Phi }_2\cup E^{\ast }\left(G\right)$ is an LKG cover of $G$ with ${\gamma }_{\Phi }\left(G\right)$-set (${\gamma }_{i\Phi }\left(G\right)$-set) $D={\cup }_{i=0}^k{D}_i\cup V\left(C\right)\cup H_1\cup H_2$ where, $H_1=\{x_w:w\in (V_1\cup V_2\cup V_3)\setminus V\left(C\right)\}$ $H_2=\{z_w:w\in V_3\setminus V\left(C\right)\}.$

Thus in either case there exists an LKG cover of $G$ and hence $G$ is an LKG graph (see Fig. 6).  □

Fig. 6 LKG covers of two different graphs constructed using the technique described in case 1 and case 2.

3 Concluding remarks

In [2], Acharya and Gupta introduced the concept of domination to graphoidally covered graphs. In [15], based on the fundamental problem of determining the graphs in which domination number equals the independent domination number, the concept of least kernel graphoidal graphs (LKG graphs) was introduced. In this paper, extending the work in [15], we found a necessary condition for a graph to be an LKG graph. Also, we have not found any graph which does not possess LKG cover and satisfies the condition of Theorem 2.5. Hence we conjecture

Conjecture 1

A graph $G$ is an LKG graph if and only if $G$ is not having $K_4^{4+}$ as its subgraph such that pendant vertices of $K_4^{4+}$ are pendant vertices in $G$.

We showed that due to Allan Laskar Theorem, the trivial graphoidal cover of every claw-free is an LKG cover and hence every claw free is an LKG graph. But then one may be tempted to ask does every claw free graph possess a non-trivial LKG cover? Also, one may look for graphs in which every graphoidal cover is an LKG cover. Further, all these problems can be seen in terms of acyclic graphoidal covers of a graph.

If $G$ is a graph having a graphoidal cover $\Psi$ such that ${\gamma }_{\Psi }\left(G\right)=1$, then $\Psi$ is an LKG cover of $G$ and consequently, $G$ is an LKG graph. Also, a graph $G$ which possesses a graphoidal cover $\Psi$ such that $V\left(G\right)$ is the only $\Psi$-dominating set of $(G,\Psi )$ is trivially an LKG graph with $\Psi$ being one of its LKG cover. B.D Acharya, et al. in [12,13], have obtained characterization for such graphs.

Notes

Peer review under responsibility of Kalasalingam University.