Structure connectivity of hypercubes

Peer review under responsibility of Kalasalingam University.

Abstract

The connectivity of a graph is an important measurement for the fault-tolerance of the network. To provide more accurate measures for the fault-tolerance of networks than the connectivity, some generalizations of connectivity have been introduced. Let $H$ be a connected subgraph of a graph $G$. A set $F$ of a connected subgraphs of $G$ is called a subgraph cut of $G$ if $G-F$ is either disconnected or trivial. If further, each member of $F$ is isomorphic to $H$, then $F$ is called an $H$-structure cut of G. The $H$-structure connectivity $\kappa (G;H)$ of $G$ is the minimum cardinality of an $H$-structure cut of $G$. In this paper we determine $\kappa (Q_n;H)$ or its upper bound where $Q_n$ is the $n$-dimensional hypercube with $n\ge 4$ and $H$ is either $Q_m$ with $m\le n-2$ or even cycle $C_l$ with $l\le 2^n$.

Keywords:

• Structure connectivity
• Cycle
• Hypercube

1 Introduction

In the design of an interconnection system, one important consideration is that the network should be least vulnerable to any disruption. The ability of a system to continue operations correctly in the presence of failures in one or many of its components is known as fault tolerance. The connectivity is one of the essential parameters to evaluate the fault tolerance of a network. To make an overall evaluation of an interconnection network with failures, some other measures related to connectivity have been introduced and studied in recent years [1–3^[1][2][3]].

Lin et al. [4] introduced a new kind of connectivity called structure connectivity. According to them, a set $F$ of connected subgraphs of $G$ is a subgraph cut of $G$ if $G-V\left(F\right)$ is disconnected or trivial graph. Let $H$ be a connected subgraph of $G$. Then $F$ is an $H$-structure-cut if $F$ is subgraph cut, and every element in $F$ is isomorphic to $H$. They defined the $H$-structure connectivity of $G$ denoted by $\kappa (G;H)$, to be the minimum cardinality of all $H$-structure-cuts of $G$. This study was motivated by the trend that networks and subnetworks of large scales are increasingly made into chips, and it is becoming more and more feasible to consider the fault status of a structure, rather than individual nodes. They obtained $\kappa (Q_n;H)$ for each $H\in (K_1,K_{1,1},K_{1,2},K_{1,3},C_4)$.

In this paper, we determine $\kappa (Q_n;H)$ or its upper bound where $Q_n$ is the $n$-dimensional hypercube with $n\ge 4$ and $H$ is $Q_m$ where $m\le n-2$ and an even cycle $C_l$ with $l\le 2^n$.

For a positive integer $n$, we denote the hypercube graph $Q_n$ whose vertex set i.e. $V\left(Q_n\right)=\{u=u_1{u}_2\dots u_n:u_k\in \{0,1\},1\le k\le n\}$ consisting of binary strings of length $n$. Two strings are adjacent if they differ in exactly one-bit position. $Q_n$ has many attractive properties, such as being bipartite, $n$-regular, $n$-connected, edge-bipancyclic. Due to these and many more attractive topological properties, hypercube has been one of the most fundamental interconnection networks.

We decompose $Q_n=Q_m\square Q_{n-m}$. Now, for any $t\in V\left(Q_{n-m}\right)$ we denote by $(Q_m,t)$ the subgraph of $Q_n$ induced by the vertices whose last $n-m$ components form the tuple $t$. It is easy to observe that $(Q_m,t)$ is isomorphic to $Q_m$.

For undefined terminology and notations see [4,5].

2 Structure connectivity of hypercubes

Theorem 2.1

Let $n\ge 4$ be an integer. Then for each $1\le m\le (n-2)$, $\kappa (Q_n;Q_m)=n-m$ and $\kappa (Q_n;C_{2^m})\le n-m$.

Proof

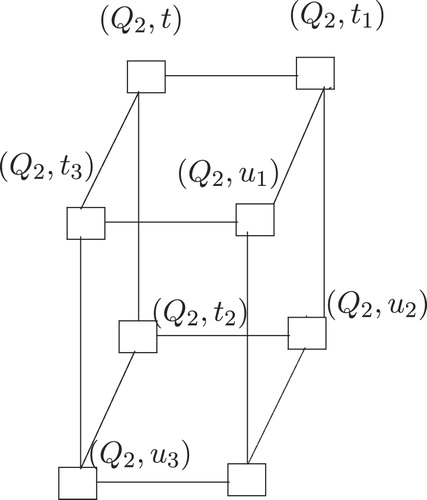
Let $Q_n=Q_m\square Q_{n-m}$. As $Q_{n-m}$ is $(n-m)$-regular and $(n-m)$-connected, every vertex in $V\left(Q_{n-m}\right)$ is adjacent to exactly $n-m$ number of vertices. Let $t\in V\left(Q_{n-m}\right)$ be adjacent to $t_1,t_2,\dots ,t_{(n-m)}\in V\left(Q_{n-m}\right)$. Hence induced subgraph $(Q_m,t)$ of $Q_n$ is adjacent to exactly $(n-m)$ subcubes namely $(Q_m,t_1),(Q_m,t_2),\dots ,(Q_m,t_{(n-m)})$ (see Fig. 1 for an illustration). Clearly, removal of ${\bigcup }_{i=1}^{n-m}(Q_m,t_i)$ disconnects $Q_n$. Thus, $\kappa (Q_n;Q_m)\le n-m$. If $\kappa (Q_n;Q_m)<n-m$, then without loss of generality one can assume that removal of ${\bigcup }_{i=2}^{n-m}(Q_m,t_i)$ disconnects $Q_n$. Hence the removal of ${\bigcup }_{i=2}^{n-m}{t}_i$ will disconnect $Q_{n-m},$ a contradiction to $Q_{n-m}$ is $(n-m)$-connected. Hence $\kappa (Q_n;Q_m)=n-m.$

Since $Q_{n-m}$ is Hamiltonian, it contains a spanning cycle of length $2^{n-m}$. Removal of isomorphic Hamiltonian cycles of all subcubes $(Q_m,t_1),(Q_m,t_2),\dots ,(Q_m,t_{(n-m)})$ disconnect $Q_n$. Hence $\kappa (Q_n;C_{2^m})\le n-m$.  □

Fig. 1 $Q_5=Q_2\square Q_3$.

Proposition 2.2

Let $n\ge 5$ be an integer. Then for any integer $m$ with $2\le m\le n-2$ and for any even integer $k$ with $2^m<k<2^{m+1},$ $\kappa (Q_n;C_k)\le n-m$.

Proof

Let $Q_n=Q_m\square Q_{n-m}$ ($2\le m\le n-2$). Let $t\in V\left(Q_{n-m}\right)$ be adjacent to $n-m$ number of vertices say $t_1,t_2,\dots ,t_{(n-m)}$. It is well known that hypercube is a bipartite graph so, $t_i$ is not adjacent to $t_j$ for all $i\ne j$ ($1\le i,j\le n-m$). Also, every pair of adjacent edges lies in exactly one $4$-cycle [6]. Hence we name vertices say $u_1,u_2,\dots ,u_{(n-m)}$ from $V\left(Q_{n-m}\right)$ such that $t_i$ is adjacent to say $u_i$ for all $1\le i\le n-m$ (see Fig. 1 for an illustration).

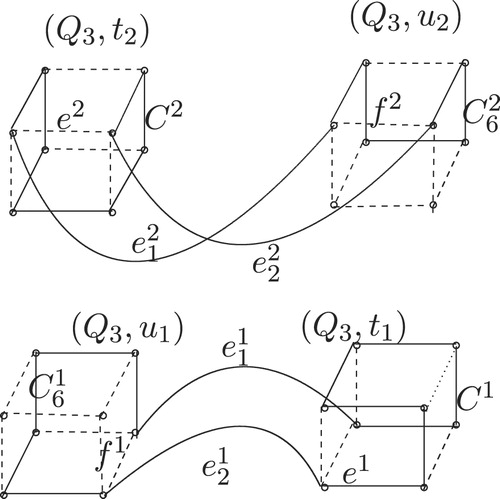
In the case when $n-m=2$, we take vertices of $Q_{n-m}=Q_2$ as $t_1,u_1,t_2,u_2$. Hence the $4-$cycle in $Q_2$ we take as $t_1{u}_1{t}_2{u}_2{t}_1$. See Fig. 2.

The construction of cycles of length $2^m+l$ for every even integer $l$ ($2\le l\le 2^m-2$) proceeds as follows. We start by choosing an arbitrary Hamiltonian cycle say $C^i$ of $(Q_m,t_i)$ for every $i$ ($1\le i\le n-m$). Then we choose any edge say $e^i$ on $C^i$ and its corresponding edge $f^i$ in $(Q_m,u_i)$. As $(Q_m,u_i)$ is an edge-bipancyclic graph there exist cycles $C_l^i$ of length $l$ for every even integer $l$ ($2\le l\le 2^m-2$) containing $f^i$. Therefore by gluing cycles $C^i$ and $C_l^i$ in the following manner $(C^i-e^i)+e_1^i+e_2^i+(C_l^i-f^i)$, we obtain a cycle $C_k^i$ of length $k=2^m+l$ ($4\le l\le 2^m-2$), for $l=2$ glue cycle $C^i$ with an edge $e^{\prime }$. (See Fig. 2 for illustration of $Q_5$. In this figure two cycles of length $12$ are shown by solid lines. It can be checked that by removal of these cycles, $Q_5$ gets disconnected.)

It is easy to observe that removal of cycles $C_k^i$ for all $i$, $1\le i\le n-m$ disconnect $Q_n$.  □

Fig. 2 $Q_5=Q_3\square Q_2$.

Note: In case of $Q_4$, it can be easily observed that $\kappa (Q_4;C_6)=2$.

Proposition 2.3

Let $n\ge 4$ be an integer. Then for every even integer $k$ with $2^{n-1}+2\le k\le 2^n-4$, $\kappa (Q_n;C_k)=1$.

Proof

Let $Q_n=Q_{n-2}\square Q_2$. Let $t_i\in V\left(Q_2\right):1\le i\le 4$ and let $t_1{t}_2{t}_3{t}_4{t}_1$ be the $4-$cycle in $Q_2$. Denote by $R_{ij}$ the set of cross edges between $(Q_{n-2},t_i)$ and $(Q_{n-2},t_j)$ for $j=i+1$ and $1\le i\le 3$.

We start by choosing an arbitrary Hamiltonian cycle say $C^1$ of $(Q_{n-2},t_1)$ and choose any edge say $e$ on $C^1$. Consider an edge $f\in E(Q_{n-2},t_2)$ which is corresponding to the edge $e$. As $(Q_{n-2},t_2)$ is an edge-bipancyclic graph, there exist cycles $C_l^2$ of length $l$ for every even integer $l$ ($2\le l\le 2^{n-2}-2$) containing an edge $f$. Let $f^l\ne f$ is an edge on $C_l^2$ which is nonadjacent to $f$. Denote by $g^l\in E(Q_{n-2},t_3)$ the corresponding edge of $f^l$ and let $C^3$ be a Hamiltonian cycle of $(Q_{n-2},t_3)$ containing $g^l$. Let an edge $g\ne g^l$ be some another nonadjacent edge on $C^3$. Now denote by $h\in E(Q_{n-2},t_4)$ the corresponding edge of $g$ and cycles of length $l$ for every even integer $l$ ($2\le l\le 2^{n-2}-2$) by $C_l^4$ which contain an edge $h$. Note that $e_1,e_2\in R_{12},f_1,f_2,f_1^l,f_2^l\in R_{23},g_1,g_2,g_1^l,g_2^l\in R_{34}$ and $h_1,h_2\in R_{41}$.

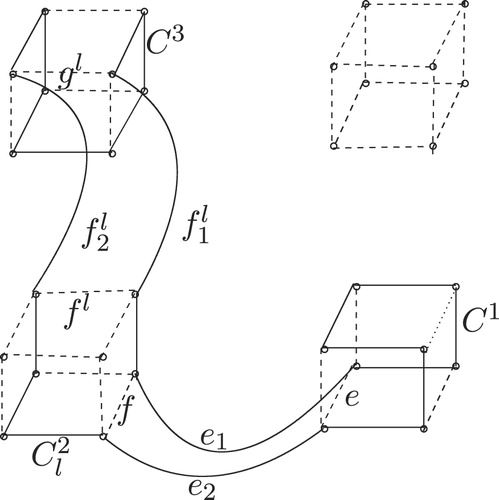
The construction of cycles of even length $k$, with $2^{n-1}+2\le k\le 2^n-4$, proceeds as follows.

$1$: By gluing cycles $C^1$ and $C^3$ in the following manner $C_k=(C^1-e)+e_1+e_2+(C_l^2-f-f^l)+f_1^l+f_2^l+(C^3-g^l)$ for every even integer $k$ with $2^{n-1}+4\le k\le 2^{n-1}+2^{n-2}-2$. (See Fig. 3 for an illustration. In Fig. 3 we have shown the effect of removal of a cycle of length $22$ from $Q_5=Q_3\square Q_2$.)

$2$: $C_k=(C^1-e)+e_1+e_2+(C_{2^{n-2}-2}^2-f-f^l)+f_1^l+f_2^l+(C^3-g^l-g)+g_1+g_2+(C_l^4-h)$ for every even integer $k$ with $2^{n-1}+2^{n-2}+2\le k\le 2^n-4$.

$3$: for $k=2^{n-1}+2^{n-2}$, we construct $C_k=(C^1-e)+e_1+e_2+(C_{2^{n-2}-2}^2-f-f^l)+f_1^l+f_2^l+(C^3-g^l-g)+g_1+g_2+\left(h\right)$.

Lastly,

$4$: For $k=2^{n-1}+2$, we proceed in the following manner $C_k=(C^1-e)+e_1+e_2+f_1+f_2+(C^3-g)$. Here, we consider $C^1$, $C^2$ and $C^3$ are all corresponding Hamiltonian cycles (isomorphic to each other) and $f,e_1$ and $f_1$ have one common vertex on $C^2$ as well $g,e_2$ and $f_2$ have one common vertex on $C^3$.  □

Fig. 3 Bold lines represent cycle $C_k$ to remove.

3 Concluding remarks

In this paper, we obtained $\kappa (Q_n;H)$ or its upper bound where $Q_n$ ($n\ge 4$) denotes hypercube, $H$ is either a hypercube $Q_m$ for $1\le m\le (n-2)$ or a cycle $C_l$ of length $l$ where $l$ is even and $2\le l\le 2^n$.

But the question still remains open $1$. For $n\ge 4$ and for each $1\le m\le n-2$, can we prove $\kappa (Q_n;C_{2^m})=n-m$?

Also, we can ask the same type of questions in the case of numerous variations of the hypercube.

Notes

Peer review under responsibility of Kalasalingam University.