Generalized projections in Zn

Peer review under responsibility of Kalasalingam University.

Abstract

We consider the ring ${\mathbb{Z}}_n$ (integers modulo $n$) with the partial order ‘$\le$’ given by ‘$a\le b$ if either $a=b$ or $a\equiv ab\left(modn\right)$’. In this paper, we obtain necessary and sufficient conditions for the poset (${\mathbb{Z}}_n,\le$) to be a lattice.

Keywords:

• Generalized projections
• Regular elements
• Nilpotent elements

1 Introduction

An element $a$ in a commutative ring $R$ is said to be a generalized projection if $a^k=a$ for some $k\in \mathbb{N}$ with $k\ge 2$ (see [1]); an element $a$ is called a regular element if $a=aba(=a^{2}b)$ for some element $b$ in the ring. It is proved by L$\acute{\text{a}}$szl$\acute{\text{o}}$ T$\acute{\text{o}}$th [2] that in ${\mathbb{Z}}_n$, an element is a generalized projection if and only if it is regular; in-fact the following result is proved.

Theorem 1.1

[2], Theorem 1

Let $n={\prod }_{i=1}^k{p}_i^{{\alpha }_i}$ be the prime factorization of $n\in \mathbb{N}$ with ${\alpha }_i>0$, for all $i$. For an integer $a\ge 1$, the following assertions are equivalent:

(i) $a$ is regular (mod $n$); (ii) for every $i\in 1,2,\dots ,k$, either $p_i^{{\alpha }_i}a$ or $p_i\nmid a$;

(iii) $gcd(a,n)=gcd(a^2,n)$; (iv) $gcd(a,n)n$ and $gcd(gcd(a,n),\frac{n}{gcd(a,b)})=1$;

(v) $a^{\phi \left(n\right)+1}\equiv a\left(modn\right)$; (vi) there exists an integer $m\ge 1$ such that $a^{m+1}\equiv a\left(modn\right)$.

We denote by $GP\left({\mathbb{Z}}_n\right)$, the set of generalized projections (i.e. the set of regular elements) and $P\left({\mathbb{Z}}_n\right)=a\in {\mathbb{Z}}_n{a}^2=a$, the set of projections in ${\mathbb{Z}}_n$. Let $R$ be a commutative ring, the relation ‘$\le$’ defined by: for $a,b\in R$, ‘$a\le b$ if and only if either $a=b$ or $a=ab$’ is a partial order on $R$ (see [1]). In particular, $({\mathbb{Z}}_n,\le )$ is a poset with the smallest element $0$ and the largest element $1$. It is known that $(P\left({\mathbb{Z}}_n\right),\le )$ is a lattice. However, Khairnar and Waphare [1] proved that for any finite commutative ring $R$, $(GP\left(R\right),\le )$ is a lattice, hence in particular, $(GP\left({\mathbb{Z}}_n\right),\le )$ is a lattice for every $n$. Whenever $n$ is a square-free integer, we get that $GP\left({\mathbb{Z}}_n\right)={\mathbb{Z}}_n$. 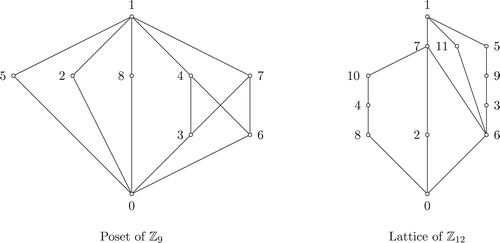In general, $({\mathbb{Z}}_n,\le )$ is not a lattice, for example $({\mathbb{Z}}_9,\le )$ (see Fig. 2). In this paper, we give necessary and sufficient conditions for the poset (${\mathbb{Z}}_n,\le$) to be a lattice.

Fig. 2 Poset of ${\mathbb{Z}}_9$ and Lattice of ${\mathbb{Z}}_{12}$.

We denote by $U\left({\mathbb{Z}}_n\right)$, the set of units in ${\mathbb{Z}}_n$ and $N\left({\mathbb{Z}}_n\right)$, the set of nilpotents in ${\mathbb{Z}}_n$. In the following remark, we list observations required in a sequel.

Remark 1.2

Let $n={\prod }_{i=1}^k{p}_i^{{\alpha }_i}$ be the prime factorization of $n\in \mathbb{N}$ with ${\alpha }_i>0$, for all $i$, and let $a\in {\mathbb{Z}}_n$. Then,

(i) $a\in U\left({\mathbb{Z}}_n\right)$ if and only if $a\equiv$ unit (mod $p_i$) for all $i\in 1,2,\dots ,k$.

(ii) $a\in N\left({\mathbb{Z}}_n\right)$ if and only if $a\equiv$ zero (mod $p_i$) for all $i\in 1,2,\dots ,k$.

(iii) $a\in GP\left({\mathbb{Z}}_n\right)$ if and only if $a\equiv$ zero or unit (mod $p_i^{{\alpha }_i}$) for all $i\in 1,2,\dots ,k$.

2 Upper covering projection and lower covering projection

In a poset $(P,\le )$, $a<b$ denotes $a\le b$ with $a\ne b$. We say that $b$ is an upper cover of $a$ or $a$ is a lower cover of $b$ (denoted by $a\prec b$), if $a<b$ and there is no $c\in P$ such that $a<c<b$.

The following theorem gives an existence of the unique lower cover and the unique upper cover of any element $a\in GP\left(R\right)\setminus P\left(R\right)$ in the poset $GP\left(R\right)$.

Theorem 2.1

[1], Theorem 2.7

Let $R$ be a finite commutative ring. If $a\in GP\left(R\right)\setminus P\left(R\right)$, then there exist a unique $a_u\in GP\left(R\right)$ and a unique $a_l\in GP\left(R\right)$ such that $a_l\prec a\prec a_u$. Further, these unique elements are projections and for $b\in GP\left(R\right)$, $a<b$ if and only if $a_u\le b$; and $b<a$ if and only if $b\le a_l$.

With notations as in Theorem 2.1, the unique projection $a_l$ is called the lower covering projection of $a$ and the unique projection $a_u$ is called the upper covering projection of $a$. If $a$ is a projection, then we assume that the lower covering projection of $a$ and the upper covering projection of $a$ is $a$ itself.

Theorem 2.1 gives an existence of the upper covering projection and the lower covering projection of any element in $GP\left({\mathbb{Z}}_n\right)\setminus P\left({\mathbb{Z}}_n\right)$. In this section, we determine the upper covering projection and the lower covering projection of elements in $GP\left({\mathbb{Z}}_n\right)\setminus P\left({\mathbb{Z}}_n\right)$.

The following lemma gives the conditions for strict comparability of a projection and a generalized projection.

Lemma 2.2

Let $n={\prod }_{i=1}^k{p}_i^{{\alpha }_i}$ be the prime factorization of $n\in \mathbb{N}$ with ${\alpha }_i>0$, for all $i$. Let $a\in GP\left({\mathbb{Z}}_n\right)$ and $e,f\in P\left({\mathbb{Z}}_n\right)\setminus 1$. Then,

(1) $a<e$ if and only if for $i\in 1,2,\dots ,k$, $e\equiv 0\left(mod{p}_i^{{\alpha }_i}\right)$ implies that $a\equiv 0\left(mod{p}_i^{{\alpha }_i}\right)$.

(2) $f<a$ if and only if for $j\in 1,2,\dots ,k$, $f\not\equiv 0\left(mod{p}_j^{{\alpha }_j}\right)$ implies that $a\equiv 1\left(mod{p}_j^{{\alpha }_j}\right)$.

Proof

$\left(1\right)$ Let $a<e$ and $i\in 1,2,\dots ,k$ be such that $e\equiv 0\left(mod{p}_i^{{\alpha }_i}\right)$. Then $a(1-e)\equiv 0\left(modn\right)$ and $1-e\not\equiv 0\left(mod{p}_i^{{\alpha }_i}\right)$. Therefore $a\equiv 0\left(mod{p}_i^{{\alpha }_i}\right)$. Conversely, suppose that for $i\in 1,2,\dots ,k$, $e\equiv 0\left(mod{p}_i^{{\alpha }_i}\right)$ implies that $a\equiv 0\left(mod{p}_i^{{\alpha }_i}\right)$. Then $a(1-e)\equiv 0\left(modn\right)$. Thus $a<e$.

$\left(2\right)$ Let $f<a$ and $j\in 1,2,\dots ,k$ be such that $f\not\equiv 0\left(mod{p}_j^{{\alpha }_j}\right)$. Then $1-a\equiv 0\left(mod{p}_j^{{\alpha }_j}\right)$. Therefore $a\equiv 1\left(mod{p}_j^{{\alpha }_j}\right)$. Conversely, suppose that for $j\in 1,2,\dots ,k$, $f\not\equiv 0\left(mod{p}_j^{{\alpha }_j}\right)$ implies that $a\equiv 1\left(mod{p}_j^{{\alpha }_j}\right)$. This gives $f(1-a)\equiv 0\left(modn\right)$. Thus $f<a$. □

Remark 2.3

[1], Remark 3

Let $a\in GP\left({\mathbb{Z}}_n\right)$. Suppose $k\ge 2$ be the smallest integer such that $a^k=a$. Then ${\left(a^{k-1}\right)}^2=a^{2k-2}=a^k{a}^{k-2}=a{a}^{k-2}=a^{k-1}$. Therefore $a^{k-1}\in P\left({\mathbb{Z}}_n\right)$, and $a^{k-1}=a_u$. Clearly, $a\le a_u$; and $a=a_u$ if and only if $a\in P\left({\mathbb{Z}}_n\right)$.

For any $a\in GP\left({\mathbb{Z}}_n\right)\setminus P\left({\mathbb{Z}}_n\right)$ the following theorem gives a construction for $a_u$.

Theorem 2.4

Let $n={\prod }_{i=1}^k{p}_i^{{\alpha }_i}$ be the prime factorization of $n\in \mathbb{N}$ with ${\alpha }_i>0$, for all $i$, and $a\in GP\left({\mathbb{Z}}_n\right)\setminus P\left({\mathbb{Z}}_n\right)$. If $a\in U\left({\mathbb{Z}}_n\right)$, then $a_u=1$. If $a\notin U\left({\mathbb{Z}}_n\right)$, then $a_u=b^{\phi \left(\frac{n}{b}\right)}$ where $b={\prod }_{\genfrac{}{}{0ex}{}{j=1}{a\equiv 0\left(mod{p}_j^{{\alpha }_j}\right)}}^k{p}_j^{{\alpha }_j}$.

Proof

Let $a\in GP\left({\mathbb{Z}}_n\right)\setminus P\left({\mathbb{Z}}_n\right)$. If $a\in U\left({\mathbb{Z}}_n\right)$ then by Remark 2.3, $a_u=1$. Suppose $a\notin U\left({\mathbb{Z}}_n\right)$. By Remark 1.2, there exists $j\in 1,2,\dots ,k$ such that $a\equiv 0\left(mod{p}_j^{{\alpha }_j}\right)$, and $a\equiv 0orunit\left(mod{p}_i^{{\alpha }_i}\right)$ for all $i\ne j$. Let $b={\prod }_{\genfrac{}{}{0ex}{}{j=1}{a\equiv 0\left(mod{p}_j^{{\alpha }_j}\right)}}^k{p}_j^{{\alpha }_j}$ and $a_u=b^{\phi \left(\frac{n}{b}\right)}$. Then $a_u\in P\left({\mathbb{Z}}_n\right)$ and by Lemma 2.2, $a\le a_u$. Let $e\in P\left({\mathbb{Z}}_n\right)$ be such that $a<e$. If $e=1$, then $a_u\le e$. Suppose $e\ne 1$. Again by Lemma 2.2, for $i\in 1,2,\dots ,k$, $e\equiv 0\left(mod{p}_i^{{\alpha }_i}\right)$ implies that $a\equiv 0\left(mod{p}_i^{{\alpha }_i}\right)$. Thus $a_u\le e$. □

For any $a\in GP\left({\mathbb{Z}}_n\right)\setminus P\left({\mathbb{Z}}_n\right)$ the following theorem gives a construction for $a_l$.

Theorem 2.5

Let $n={\prod }_{i=1}^k{p}_i^{{\alpha }_i}$ be the prime factorization of $n\in \mathbb{N}$ with ${\alpha }_i>0$, for all $i$, and $a\in GP\left({\mathbb{Z}}_n\right)\setminus P\left({\mathbb{Z}}_n\right)$. Then $a_l=b^{\phi \left(\frac{n}{b}\right)}$ where $b={\prod }_{\genfrac{}{}{0ex}{}{j=1}{a\not\equiv 1\left(mod{p}_j^{{\alpha }_j}\right)}}^k{p}_j^{{\alpha }_j}$.

Proof

Let $a\in GP\left({\mathbb{Z}}_n\right)\setminus P\left({\mathbb{Z}}_n\right)$. If $a\equiv 1\left(mod{p}_j^{{\alpha }_j}\right)$ for all $j\in 1,2,\dots ,k$ then $a-1\equiv 0\left(modn\right)$. Hence $a=1\in P\left({\mathbb{Z}}_n\right)$, a contradiction. Therefore there exists $j\in 1,2,\dots ,k$ such that $a\not\equiv 1\left(mod{p}_j^{{\alpha }_j}\right)$. Let $b={\prod }_{\genfrac{}{}{0ex}{}{j=1}{a\not\equiv 1\left(mod{p}_j^{{\alpha }_j}\right)}}^k{p}_j^{{\alpha }_j}$ and $a_l=b^{\phi \left(\frac{n}{b}\right)}$. We prove that $a_l\le a$. Let $i\in 1,2,\dots ,k$ be such that $a_l\not\equiv 0\left(mod{p}_i^{{\alpha }_i}\right)$. Then $b\not\equiv 0\left(mod{p}_i^{{\alpha }_i}\right)$ and hence $a\equiv 1\left(mod{p}_i^{{\alpha }_i}\right)$. This yields, $a_l(a-1)\equiv 0\left(modn\right)$. Therefore $a_l\le a$. Let $f\in P\left({\mathbb{Z}}_n\right)$ be such that $f<a$, and $j\in 1,2,\dots ,k$ be such that $f\not\equiv 0\left(mod{p}_j^{{\alpha }_j}\right)$. Then by Lemma 2.2, we get $a\equiv 1\left(mod{p}_j^{{\alpha }_j}\right)$. Consequently, $b\not\equiv 0\left(mod{p}_j^{{\alpha }_j}\right)$ and hence $a_l\not\equiv 0\left(mod{p}_j^{{\alpha }_j}\right)$. This implies that $a_l\equiv 1\left(mod{p}_j^{{\alpha }_j}\right)$. Therefore $f(1-a_l)\equiv 0\left(modn\right)$. Thus $f\le a_l$. □

Let $P$ be a poset and $a,b\in P$. The join of $a$ and $b$ if exists, denoted by $a\vee b$, is defined as $a\vee b=supa,b$. The meet of $a$ and $b$ if exists, denoted by $a\wedge b$, is defined as $a\wedge b=infa,b$.

We conclude this section with the following examples.

In the following example, $n\in \mathbb{N}$ is not square-free but the poset ${\mathbb{Z}}_n$ is a lattice.

Example 2.6

Consider the ring ${\mathbb{Z}}_4$. Then $GP\left({\mathbb{Z}}_4\right)=0,1,3$ and $N\left({\mathbb{Z}}_4\right)=0,2$. Note that $4$ is not square-free but the poset ${\mathbb{Z}}_4$ is a lattice (see Fig. 1). Also, the nilpotent element $2$ possess unique upper cover.

Fig. 1 Lattices of ${\mathbb{Z}}_4$ and ${\mathbb{Z}}_8$.

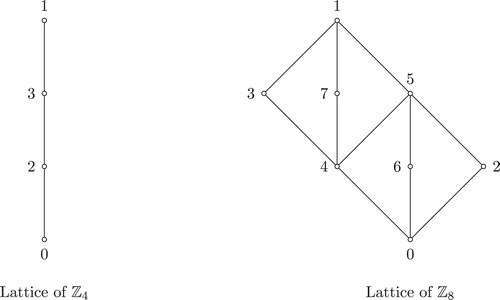
Example 2.7

Consider the ring ${\mathbb{Z}}_8$. Then $GP\left({\mathbb{Z}}_8\right)=0,1,3,5,7$ and $N\left({\mathbb{Z}}_8\right)=0,2,4,6$. Note that $8$ is not square-free but the poset ${\mathbb{Z}}_8$ is a lattice (see Fig. 1). Also, each of $2$ and $6$ possesses unique upper covers but $4$ does not possess unique upper cover.

In the following example, the poset ${\mathbb{Z}}_n$ is not a lattice. Also, none of the nilpotent elements possess unique upper cover.

Example 2.8

Consider the ring ${\mathbb{Z}}_9$. Then $GP\left({\mathbb{Z}}_9\right)=0,1,2,4,5,7,8$ and $N\left({\mathbb{Z}}_9\right)=0,3,6$. By Fig. 2, the poset ${\mathbb{Z}}_9$ is not a lattice. Note that $3\vee 6$ and $4\wedge 7$ do not exist. Also, each of $3$ and $6$ do not possess unique upper covers and each of $4$ and $7$ do not possess unique lower covers.

In the following example, $n$ is not square-free but the poset ${\mathbb{Z}}_n$ is a lattice.

Example 2.9

Consider the ring ${\mathbb{Z}}_{12}$. Then $GP\left({\mathbb{Z}}_{12}\right)=0,1,3,4,5,7,8,9,11$ and $N\left({\mathbb{Z}}_{12}\right)=0,6$. Note that $12$ is not square-free but the poset ${\mathbb{Z}}_{12}$ is a lattice (see Fig. 2). Observe that, the nilpotent element $6$ does not possess an unique upper cover.

Theorem 2.10

Let $({\mathbb{Z}}_n,\le )$ be a poset and $a\in {\mathbb{Z}}_n$. If $a$ is a dual atom then $a\in GP\left({\mathbb{Z}}_n\right)$.

Proof

If $a\in P\left({\mathbb{Z}}_n\right)$ then $a\in GP\left({\mathbb{Z}}_n\right)$. Suppose $a\notin P\left({\mathbb{Z}}_n\right)$. So $a$ is a dual atom if and only if $a<x$ implies that $x=1$ if and only if $a\equiv ax\left(modn\right)$ implies that $x=1$ if and only if $a(1-x)\equiv 0\left(modn\right)$ implies that $x=1$ if and only if $a$ is not a zero divisor if and only if $a$ is an unit. Hence $a\in GP\left({\mathbb{Z}}_n\right)$. □

In the next section, we give a necessary and sufficient condition for the existence of supremum and infimum of any two elements of the poset ${\mathbb{Z}}_n$.

3 Existence of $a\vee b$ and $a\wedge b$ for $a,b\in {\mathbb{Z}}_n$

For $x\in {\mathbb{Z}}_n$, the ideal generated by $x$ is denoted by $\left(x\right)$.

The following theorem characterizes the existence of $a\vee b$ for $a,b\in {\mathbb{Z}}_n$.

Theorem 3.1

Let $n={\prod }_{i=1}^k{p}_i^{{\alpha }_i}$ be the prime factorization of $n\in \mathbb{N}$ with ${\alpha }_i>0$, for all $i$. Let $a,b\in {\mathbb{Z}}_n$ be incomparable and $d=gcd(gcd(a,b),n)$. Then, $a\vee b$ exists if and only if the coset $1+\left(\frac{n}{d}\right)$ has the smallest element.

Proof

For each $i\in 1,2,\dots ,k$, let ${\beta }_i,{\gamma }_i\in \mathbb{W}=\mathbb{N}\bigcup 0$ be the largest powers of prime $p_i$ such that $a\equiv 0\left(mod{p}_i^{{\beta }_i}\right)$ and $b\equiv 0\left(mod{p}_i^{{\gamma }_i}\right)$ respectively. Let $f_i=max({\alpha }_i-{\beta }_i),({\alpha }_i-{\gamma }_i),0$ and $m={\prod }_{i=1}^k{p}_i^{f_i}$. Then $m=\frac{n}{d}$. Let $c\in {\mathbb{Z}}_n$ and for each $i\in 1,2,\dots ,k$, let $t_i\in \mathbb{N}$ be the largest powers of the prime $p_i$ such that $c\equiv 1\left(mod{p}_i^{t_i}\right)$. Then, $a<c$ and $b<c$, if and only if $a(c-1)\equiv 0\left(modn\right)$ and $b(c-1)\equiv 0\left(modn\right)$, if and only if $t_i\ge ({\alpha }_i-{\beta }_i),({\alpha }_i-{\gamma }_i)$ for all $i$, if and only if $c-1\in \left(\frac{n}{d}\right)$, if and only if $c\in 1+\left(\frac{n}{d}\right)$.

Suppose $a\vee b$ exists. Since $a$ and $b$ are incomparable, we have $a<a\vee b$ and $b<a\vee b$. This yields $a\vee b\in 1+\left(\frac{n}{d}\right)$. Let $x\in 1+\left(\frac{n}{d}\right)$. Then $a<x$ and $b<x$. Therefore $a\vee b\le x$. Thus $a\vee b$ is the smallest element of the coset $1+\left(\frac{n}{d}\right)$. Conversely, suppose that the coset $1+\left(\frac{n}{d}\right)$ has the smallest element, say $e\in 1+\left(\frac{n}{d}\right)$. This yields $a<e$ and $b<e$. We claim that $a\vee b=e$. Let $f\in {\mathbb{Z}}_n$ be such that $a<f$ and $b<f$. Then $f\in 1+\left(\frac{n}{d}\right)$. Therefore $e\le f$. Thus $a\vee b=e$. □

From the proof of Theorem 3.1, it is clear that, if $a\vee b$ exists, then $a\vee b$ is the least element of the coset $1+\left(\frac{n}{d}\right)$. Also, if the coset $1+\left(\frac{n}{d}\right)$ has the smallest element $e$, then $a\vee b=e$.

The following corollary is an immediate consequence of Theorem 3.1.

Corollary 3.2

Let $n\in \mathbb{N},n>1$ and $S=d\in \mathbb{N}d=gcd(gcd(a,b),n),$ for some incomparable elements $a,b\in {\mathbb{Z}}_n$ . Then, ${\mathbb{Z}}_n$ is a lattice if and only if every coset in $1+\left(\frac{n}{d}\right)d\in S$ has smallest element.

In the following theorem, we characterize the existence of $a\wedge b$ for $a,b\in {\mathbb{Z}}_n$.

Theorem 3.3

Let $n={\prod }_{i=1}^k{p}_i^{{\alpha }_i}$ be the prime factorization of $n\in \mathbb{N}$ with ${\alpha }_i>0$, for all $i$. Let $a,b\in {\mathbb{Z}}_n$ be incomparable and $d=gcd(gcd(a-1,b-1),n)$. Then, $a\wedge b$ exists if and only if the ideal $\left(\frac{n}{d}\right)$ has the largest element.

Proof

For each $i\in 1,2,\dots ,k$, let ${\beta }_i,{\gamma }_i\in \mathbb{W}$ be the largest powers of prime $p_i$ such that $a\equiv 1\left(mod{p}_i^{{\beta }_i}\right)$ and $b\equiv 1\left(mod{p}_i^{{\gamma }_i}\right)$ respectively. Let $f_i=max({\alpha }_i-{\beta }_i),({\alpha }_i-{\gamma }_i),0$ and $m={\prod }_{i=1}^k{p}_i^{f_i}$. Then $m=\frac{n}{d}$. Let $c\in {\mathbb{Z}}_n$ and for each $i\in 1,2,\dots ,k$, let $s_i\in \mathbb{N}$ be the largest powers of prime $p_i$ such that $c\equiv 0\left(mod{p}_i^{s_i}\right)$. Then, $c<a$ and $c<b$ if and only if $c(a-1)\equiv 0\left(modn\right)$ and $c(b-1)\equiv 0\left(modn\right)$ if and only if $s_i\ge ({\alpha }_i-{\beta }_i),({\alpha }_i-{\gamma }_i)$ for all $i$ if and only if $c\in \left(\frac{n}{d}\right)$.

Suppose $a\wedge b$ exists. Since $a$ and $b$ are incomparable, we have $a\wedge b<a$ and $a\wedge b<b$. This yields $a\wedge b\in \left(\frac{n}{d}\right)$. Let $x\in \left(\frac{n}{d}\right)$. Then $x<a$ and $x<b$. Therefore $x<a\wedge b$. Thus $a\wedge b$ is the largest element of the ideal $\left(\frac{n}{d}\right)$. Conversely, suppose that the ideal $\left(\frac{n}{d}\right)$ has the largest element, say $e\in \left(\frac{n}{d}\right)$. This yields $e<a$ and $e<b$. We claim that $a\wedge b=e$. Let $f\in {\mathbb{Z}}_n$ be such that $f<a$ and $f<b$. Then $f\in \left(\frac{n}{d}\right)$. Therefore $f\le e$. Thus $a\wedge b=e$. □

From the proof of Theorem 3.3, it is clear that if $a\wedge b$ exists, then $a\wedge b$ is the largest element of the ideal $\left(\frac{n}{d}\right)$. Also, if the ideal $\left(\frac{n}{d}\right)$ has the largest element $e$, then $a\wedge b=e$.

The following corollary is an immediate consequence of Theorem 3.3.

Corollary 3.4

Let $n\in \mathbb{N},n>1$ and $S^{\prime }=d\in \mathbb{N}d=gcd(gcd(a-1,b-1),n),$ for some incomparable elements $a,b\in {\mathbb{Z}}_n$ . Then, ${\mathbb{Z}}_n$ is a lattice if and only if every ideal in $\left(\frac{n}{d}\right)d\in S^{\prime }$has largest element.

Corollary 3.5

Let $n\in \mathbb{N},n>1$, $S=d\in \mathbb{N}d=gcd(gcd(a,b),n),$ for some incomparable elements $a,b\in {\mathbb{Z}}_n$ and $S^{\prime }=d\in \mathbb{N}d=gcd(gcd(a-1,b-1),n),$ for some incomparable elements $a,b\in {\mathbb{Z}}_n$ . Then, every ideal in $\left(\frac{n}{d}\right)d\in S^{\prime }$has largest element if and only if every coset in $1+\left(\frac{n}{d}\right)d\in S$has smallest element.

Proof

Follows from Corollary 3.2 and Corollary 3.2. □

The following two lemmas relate the largest element of an ideal with the smallest element of a coset and vice versa.

Lemma 3.6

Let $n=n_1{n}_2$ with $n_1\ge 1,n_2\ge 3$ and $I=\left(n_1\right)$, $J=\left(n_2\right)$. Then, the largest element of the ideal $I$ becomes the smallest element of the coset $1+J$.

Proof

Since $I=n_2\ge 3$, we have $n_1\not\equiv -n_1\left(modn\right)$. Therefore $n_1$ and $-n_1$ are distinct elements in $I$. Let $e_1{n}_1\in I$ be the largest element of $I$. Then $x_1{n}_1\le e_1{n}_1$ for all $x_1\in \mathbb{Z}$. This yields $n_1\le e_1{n}_1$ and $-n_1\le e_1{n}_1$. That is $n_1\equiv e_1{n}_1\left(modn\right)$ or $n_1\equiv n_1{e}_1{n}_1\left(modn\right)$; and $-n_1\equiv e_1{n}_1\left(modn\right)$ or $-n_1\equiv -n_1{e}_1{n}_1\left(modn\right)$. If $n_1\equiv e_1{n}_1\left(modn\right)$ and $-n_1\equiv e_1{n}_1\left(modn\right)$, then $n_1\equiv -n_1\left(modn\right)$, a contradiction to the fact that $n_2\ge 3$. Thus, either $n_1\equiv n_1{e}_1{n}_1\left(modn\right)$ or $-n_1\equiv -n_1{e}_1{n}_1\left(modn\right)$. Suppose $n_1\equiv n_1{e}_1{n}_1\left(modn\right)$. That is $n_1(e_1{n}_1-1)\equiv 0\left(mod{n}_1{n}_2\right)$. This implies that $e_1{n}_1-1\equiv 0\left(mod{n}_2\right)$, hence $e_1{n}_1\in 1+J$. Similarly, $-n_1\equiv -n_1{e}_1{n}_1\left(modn\right)$ implies that $e_1{n}_1\in 1+J$. Thus, in any case, $e_1{n}_1\in 1+J$. Let $y_2{n}_2+1\in 1+J$ be any element. Then $(y_2{n}_2+1)e_1{n}_1=y_2{n}_2{e}_1{n}_1+e_1{n}_1\equiv e_1{n}_1\left(modn\right)$. Thus $e_1{n}_1$ is the smallest element of $1+J$. □

Lemma 3.7

Let $n=n_1{n}_2$ with $n_1\ge 3,n_2\ge 1$ and $I=\left(n_1\right)$, $J=\left(n_2\right)$. Then the smallest element of the coset $1+J$ becomes the largest element of the ideal $I$.

Proof

Since $J=n_1\ge 3$, we have $n_2\not\equiv -n_2\left(modn\right)$. Therefore $n_2+1$ and $-n_2+1$ are distinct elements in the coset $1+J$. Let $e_2{n}_2+1\in 1+J$ be the smallest element of $1+J$. Then $e_2{n}_2+1\le x_2{n}_2+1$ for all $x_2\in \mathbb{Z}$. This yields $e_2{n}_2+1\le n_2+1$ and $e_2{n}_2+1\le -n_2+1$. That is $e_2{n}_2+1\equiv n_2+1\left(modn\right)$ or $e_2{n}_2+1\equiv (e_2{n}_2+1)(n_2+1)\left(modn\right)$; and $e_2{n}_2+1\equiv -n_2+1\left(modn\right)$ or $e_2{n}_2+1\equiv (e_2{n}_2+1)(-n_2+1)\left(modn\right)$. If $e_2{n}_2+1\equiv n_2+1\left(modn\right)$ and $e_2{n}_2+1\equiv -n_2+1\left(modn\right)$, then $n_2+1\equiv -n_2+1\left(modn\right)$, a contradiction to the fact that $n_1\ge 3$. Thus, either $e_2{n}_2+1\equiv (e_2{n}_2+1)(n_2+1)\left(modn\right)$ or $e_2{n}_2+1\equiv (e_2{n}_2+1)(-n_2+1)\left(modn\right)$. Suppose $e_2{n}_2+1\equiv (e_2{n}_2+1)(n_2+1)\left(modn\right)$. That is $(e_2{n}_2+1)\left(n_2\right)\equiv 0\left(mod{n}_1{n}_2\right)$. This implies that $e_2{n}_2+1\equiv 0\left(mod{n}_1\right)$, hence $e_2{n}_2+1\in I$. Similarly, $e_2{n}_2+1\equiv (e_2{n}_2+1)(-n_2+1)\left(modn\right)$ implies that $e_2{n}_2+1\in I$. Thus, in any case, $e_2{n}_2+1\in I$. Let $y_1{n}_1\in I$ be any element. Then $\left(y_1{n}_1\right)(e_2{n}_2+1)=y_1{n}_1{e}_2{n}_2+y_1{n}_1\equiv y_1{n}_1\left(modn\right)$. Thus $e_2{n}_2+1$ is the largest element of $I$. □

Remark 3.8

Let $a\in GP\left({\mathbb{Z}}_n\right)$ and $I$ be the ideal generated by $a$. Then $a_u$ is the largest element of $I$. For $ma\in I$, $ma{a}_u=ma$, hence $ma\le a_u$.

If $a,b\in GP\left({\mathbb{Z}}_n\right)$ then $a\vee b$ and $a\wedge b$ both exist in the poset $GP\left({\mathbb{Z}}_n\right)$ (see [1]). The following two theorems give the existence of $a\vee b$ and $a\wedge b$ in the poset ${\mathbb{Z}}_n$ where $a,b\in GP\left({\mathbb{Z}}_n\right)$.

Theorem 3.9

If $a,b\in GP\left({\mathbb{Z}}_n\right)$ then $a\vee b$ exists in the poset ${\mathbb{Z}}_n$. Further, $a\vee b\in GP\left({\mathbb{Z}}_n\right)$.

Proof

If $a$ and $b$ are comparable then clearly $a\vee b$ exists and $a\vee b\in GP\left({\mathbb{Z}}_n\right)$. Suppose $a$ and $b$ are incomparable. Let $d=gcd(gcd(a,b),n)$, $I$ be the ideal generated by $d$ and $J$ be the ideal generated by $\frac{n}{d}$. As, $a,b\in GP\left({\mathbb{Z}}_n\right)$, by Remark 1.2 (iii), $gcd(a,b)\in GP\left({\mathbb{Z}}_n\right)$. Therefore $d\in GP\left({\mathbb{Z}}_n\right)$. By Remark 3.8, the ideal $I$ possesses the largest element, say $e$ and $e\in GP\left({\mathbb{Z}}_n\right)$. Since $da$ and $db$, we have $a,b\in I$. As, $a$ and $b$ are incomparable, we have $I=\frac{n}{d}\ge 3$. By Lemma 3.6, $e$ becomes the smallest element of the coset $1+J$. By Theorem 3.1, $a\vee b$ exists and $a\vee b=e$. Thus, $a\vee b=e\in GP\left({\mathbb{Z}}_n\right)$. □

Theorem 3.10

Let $a,b\in GP\left({\mathbb{Z}}_n\right)$ be such that $a-1,b-1\in GP\left({\mathbb{Z}}_n\right)$. Then $a\wedge b$ exists in the poset ${\mathbb{Z}}_n$ and $a\wedge b\in GP\left({\mathbb{Z}}_n\right)$.

Proof

If $a$ and $b$ are comparable then clearly $a\wedge b$ exists and $a\wedge b\in GP\left({\mathbb{Z}}_n\right)$. Suppose $a$ and $b$ are incomparable. Let $d=gcd(gcd(a-1,b-1),n)$ and $I$ be the ideal generated by $\frac{n}{d}$. As, $a-1,b-1\in GP\left({\mathbb{Z}}_n\right)$, by Remark 1.2 (iii), $gcd(a-1,b-1)\in GP\left({\mathbb{Z}}_n\right)$. Therefore $d\in GP\left({\mathbb{Z}}_n\right)$, and hence $\frac{n}{d}\in GP\left({\mathbb{Z}}_n\right)$. By Remark 3.8, the ideal $I$ possesses the largest element, say $e$ and $e\in GP\left({\mathbb{Z}}_n\right)$. By Theorem 3.3, $a\wedge b$ exists and $a\wedge b=e$. Thus $a\wedge b=e\in GP\left({\mathbb{Z}}_n\right)$. □

In the following theorem, we give a necessary and sufficient condition for the poset ${\mathbb{Z}}_n$ to be a lattice.

Theorem 3.11

Let $n\in \mathbb{N}$. Then, ${\mathbb{Z}}_n$ is a lattice if and only if for every $n_1\ge 3$ with $n=n_1{n}_2$, $\left(n_1\right)$ possess the largest element.

Proof

Suppose ${\mathbb{Z}}_n$ is a lattice. Let $n=n_1{n}_2$ with $n_1\ge 3$. If $\left(n_1\right)$ does not possess the largest element, then $\left(n_1\right)=n_2\ge 3$. Let $a=n_1$; and $b=p{n}_1$, where $p$ is a prime such that $gcd(p,n_2)=1$ and $n_2\nmid (p-1)$. Then $a,b\not\equiv 0\left(modn\right)$ and $a\not\equiv b\left(modn\right)$. If $a<b$, then $a\equiv ab\left(modn\right)$. That is $n_1\equiv n_{1}p{n}_1\left(modn\right)$. This yields $n_1(p{n}_1-1)\equiv 0\left(modn\right)$. This implies that $p{n}_1\equiv 1\left(mod{n}_2\right)$. Hence $gcd(n_1,n_2)=1$. Consequently $n_1\in GP\left({\mathbb{Z}}_n\right)$. By Remark 3.8, $\left(n_1\right)$ possess the largest element, a contradiction. Therefore $a\nleqq b$. Similarly, $b\nleqq a$. Thus $a$ and $b$ are incomparable. Observe that $gcd(gcd(a,b),n)=n_1$. As, $\left(\frac{n}{n_2}\right)=\left(n_1\right)$ does not possess the largest element. By Lemma 3.7, the coset $1+\left(n_2\right)$ does not possess the smallest element. By Corollary 3.2, ${\mathbb{Z}}_n$ is not a lattice, a contradiction. Therefore $\left(n_1\right)$ possess the largest element. Conversely, suppose for every $n_1\ge 3$ with $n=n_1{n}_2$, $\left(n_1\right)$ possess the largest element. If ${\mathbb{Z}}_n$ is not a lattice, then by Corollary 3.2, there exist incomparable elements $a^{\prime },b^{\prime }\in {\mathbb{Z}}_n$ such that $d^{\prime }=gcd(gcd(a^{\prime },b^{\prime }),n)$ and $1+\left(\frac{n}{d^{\prime }}\right)$ does not possess the smallest element. Therefore $\frac{n}{d^{\prime }}=\left(d^{\prime }\right)\ge 3$ and $1+\left(\frac{n}{d^{\prime }}\right)\ge 3$. Hence $\left(\frac{n}{d^{\prime }}\right)=d^{\prime }\ge 3$. Let $n_1^{\prime }=d^{\prime }$ and $n_2^{\prime }=\frac{n}{d^{\prime }}$. Then $n_1^{\prime }\ge 3$ and $n=n_1^{\prime }{n}_2^{\prime }$. By Lemma 3.6, $\left(n_1^{\prime }\right)$ does not possess the largest element, a contradiction. Thus ${\mathbb{Z}}_n$ is a lattice. □

Remark 3.12

Let $a\in N\left({\mathbb{Z}}_n\right)\setminus 0$. If $b\in {\mathbb{Z}}_n$ be such that $b<a$ then $b=ba=b{a}^m$ for any $m\in \mathbb{N}$. Since $a\in N\left({\mathbb{Z}}_n\right)$, we have $b=0$. Hence $a_l=0$. From this, it follows that, if $I$ is an ideal generated by a nilpotent element of ${\mathbb{Z}}_n$ such that $I\ge 3$, then $I$ does not possess the largest element. Thus ${\mathbb{Z}}_n$ is not a lattice.

Notes

Peer review under responsibility of Kalasalingam University.