The line completion number of hypercubes

Peer review under responsibility of Kalasalingam University.

Abstract

In 1992, Bagga, Beineke, and Varma introduced the concept of the super line graph of index $r$ of a graph $G,$ denoted by ${ℒ}_r\left(G\right).$ The vertices of ${ℒ}_r\left(G\right)$ are the $r$-subsets of $E\left(G\right),$ and two vertices $S$ and $T$ are adjacent if there exist $s\in S$ and $t\in T$ such that $s$ and $t$ are adjacent edges in $G.$ They also defined the line completion number $l_c\left(G\right)$ of graph G to be the minimum index $r$ for which ${ℒ}_r\left(G\right)$ is complete. They found the line completion number for certain classes of graphs. In this paper, we find the line completion number of hypercube $Q_n$ for every $n$.

Keywords:

• Super line graph
• Line completion number
• Induced subgraph
• Hypercube

1 Introduction

The line graph $L\left(G\right)$ of a graph $G$ is defined to have as its vertices the edges of $G,$ with two being adjacent if the corresponding edges share a vertex in $G.$ Many properties of the line graphs follow by translating the properties of the underlying graph from vertices into edges. Line graphs have been studied for over seventy five years. A motivation behind studying the line graphs had been a search for simpler algorithms for solving some hard problems.

Table

Hypercube variant	No. of vertices	No. of edges	Line completion number
Hypercube $Q_n$	$2^n$	$n\cdot 2^{n-1}$	$E\left(Q_{n-1}\right)+1$
Twisted cube $T{Q}_n$	$2^n$	$n\cdot 2^{n-1}$	$E\left(T{Q}_{n-1}\right)+1$
$k$-skipped enhanced cube $Q_{n,k}$	$2^n$	$(n+1)\cdot 2^{n-1}$	$E\left(Q_{n-1}\right)+1,$ if $k=1$
			$E\left(Q_{n-1,k-1}\right)+1,$ if $k\ne 1$
Augmented cube $A{Q}_n$	$2^n$	$(2n-1)\cdot 2^{n-1}$	$E\left(A{Q}_{n-1}\right)+1$
Möbius cube $M{Q}_n$	$2^n$	$n\cdot 2^{n-1}$	$E\left(M{Q}_{n-1}\right)+1$

Over the period, various generalizations of the line graphs have been invented and studied, including the line graphs of line graphs, line graphs of multigraphs, line graphs of hypergraphs, and line graphs of weighted graphs, etc. Prisner [1] describes many interesting generalizations of the line graphs. Bagga [2] has written a survey article on the generalizations of line graphs. In most generalizations of the line graphs, the vertices of the new graph are taken to be another family of subgraphs of $G,$ and adjacency is defined in terms of an appropriate intersection.

Bagga et al. [3] introduced the concept of the super line graph ${ℒ}_r\left(G\right)$ of a graph $G$ as follows.

Definition 1.1

For a given graph $G,$ its super line graph ${ℒ}_r\left(G\right)$ of index $r$ is the graph whose vertices are the $r$-subsets of $E\left(G\right),$ and two vertices $S$ and $T$ are adjacent if there exist $s\in S$ and $t\in T$ such that $s$ and $t$ are adjacent edges in $G.$

From the definition, it turns out that ${ℒ}_1\left(G\right)$ coincides with the line graph $L\left(G\right).$

Bagga et al. [3–8^{[3][4][5][6][7][8]}] have done extensive work on the super line graphs. They discussed various properties of super line graphs in [3,4]. In [5], they found several results on the independence number of super line graphs of arbitrary index and on pancyclicity in the index-2 case. They discussed the structure and properties of super line graphs of index $2$ at a length in [6]. K.J.Bagga and Vasquez in [9] have studied super line graphs of index $2$ for hypercubes.

One of the important properties of super line graphs is that, if ${ℒ}_r\left(G\right)$ is complete, so is ${ℒ}_{r+1}\left(G\right).$ Motivated by this, Bagga et al. [8] defined the line completion number of a graph. They determined the line completion numbers for various classes of graphs, viz., complete graph, path, cycle, fan, windmill, wheel, etc. Recently, they determined line completion number of complete bipartite graphs in [7]. Certain graphs are also characterized with the help of line completion number.

Definition 1.2

The line completion number $lc\left(G\right)$ of a graph $G$ is the least positive integer $r$ for which ${ℒ}_r\left(G\right)$ is a complete graph.

Note that the lower bound for $lc\left(G\right)$ is $1$ more than the minimum number of vertices in either of the sets that form a partition of vertex set of $G$ into two sets. For some graphs, the maximum of these numbers is the line completion number. For example, this is the case for complete graphs, and, as we shall see, for hypercubes. In this paper, we determine the line completion number of hypercube $Q_n$ for every $n.$

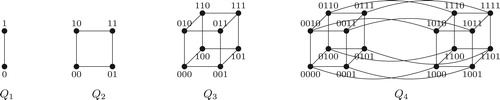
A hypercube $Q_n$ is the graph whose vertex set is the set of $2^n$ binary $n$-tuples, and edge set consists of those pairs of vertices which differ in exactly one co-ordinate. Therefore $Q_n$ is an $n$-regular graph with $2^n$ vertices and $n{2}^{n-1}$ edges. Also, for any $k\in 1,2,\dots ,n-1,$ $Q_n$ is the cartesian product of $Q_k$ and $Q_{n-k},$ i.e., $Q_n=Q_{n-k}\square Q_k.$

Fig. 1 shows some elementary hypercubes.

Fig. 1 Hypercubes.

We prove the following theorem.

Theorem

For any $n,$ $lc\left(Q_n\right)=(n-1)2^{n-2}+1.$

Interestingly, this number is $1$ more than the number of edges in the half cube $Q_{n-1}.$ For the proof, we need a result related to the maximum number of edges in an induced subgraph of $Q_n$ on $p$ vertices. Hart [10] has given the required formula, which looks simple, but is tedious to workout. We state the same result in other words and prove that both the formulae are same. We do this preliminary work out in Section 2 and proof of the theorem is given in Section 3.

2 Preliminaries

Hart [10] found a set of vertices of a given size in the hypercube which has the maximum number of interconnecting edges. He denoted for any non-negative integer $i,$ $h\left(i\right)$ as the sum of its binary digits, i.e., the number of ones there. Then one has the following obvious lemma.

Lemma 2.1

[10]

For all $r\ge 0,$ ${\sum }_{i=0}^{2^r-1}h\left(i\right)=r{2}^{r-1}.$

He proved the following proposition.

Proposition 2.2

For any $n$ and $k$ satisfying $0<k\le 2^n,$ the maximum number of edges $f\left(k\right)$ in the induced subgraph on $k$ vertices is given by $f\left(k\right)={\sum }_{i=1}^{k-1}h\left(i\right).$

Though the above formula for finding the maximum number of edges on the induced subgraph of $Q_n$ having $k$ vertices looks simple, one needs to know the binary representations of all the digits from $0$ to $k-1.$ In 2013, Li and Yang [11] found $f\left(k\right)$ in terms of the binary representation of $k$ only. We prove the same result in a much simpler way and prove that the formula which we obtain is same as the above.

Lemma 2.3

For any $p=2^{k_1}+2^{k_2}+\cdots +2^{k_m},$ with $k_1<k_2<\cdots <k_m,$ $f\left(p\right)={\sum }_{i=1}^{p-1}h\left(i\right)={\sum }_{i=1}^m{k}_i{2}^{k_i-1}+{\sum }_{i=1}^{m-1}(m-i)2^{k_i}.$

Proof

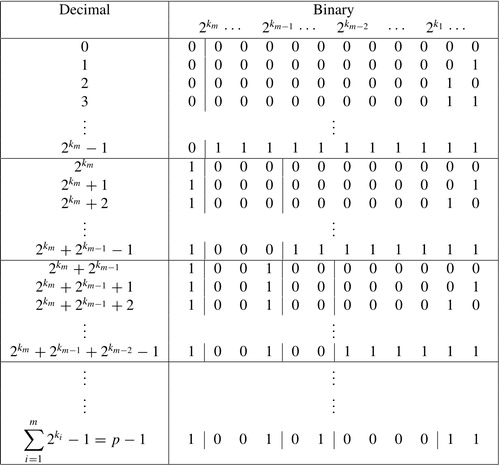
For calculating ${\sum }_{i=1}^{p-1}h\left(i\right),$ one needs to know the number of $1$’s appearing in the binary representations of all the numbers from $0$ to $p-1.$ See the table given below.

We have divided the table into blocks corresponding to the binary representations of the digits from $0$ to $2^{k_m}-1,$ $2^{k_m}$ to $2^{k_m}+2^{k_{m-1}}-1$, $2^{k_m}+2^{k_{m-1}}$ to $2^{k_m}+2^{k_{m-1}}+2^{k_{m-2}}-1$,…,$2^{k_m}+2^{k_{m-1}}+\cdots +2^{k_2}$ to $2^{k_m}+2^{k_{m-1}}+\cdots {+}^{k_1}-1.$ By Lemma 2.1, the total number of $1$’s in these blocks is equal to ${\sum }_{i=1}^m{k}_i{2}^{k_i-1}.$

In addition to them, number of $1$’s in $2^{k_m}+1^{st}$ column is equal to ${\sum }_{i=1}^{m-1}{2}^{k_i},$ number of $1$’s in $2^{k_{m-1}}+1^{st}$ column is equal to ${\sum }_{i=1}^{m-2}{2}^{k_i},$ and so on.

Therefore the total number of $1$’s in the binary representations of $0$ to $p-1$ is ${\sum }_{i=1}^m{k}_i{2}^{k_i-1}+{\sum }_{i=1}^{m-1}{2}^{k_i}+{\sum }_{i=1}^{m-2}{2}^{k_i}+\cdots +2^{k_1}.$ But on simplifying the above summations, we get the desired formula. □

3 Proof of the main theorem

Theorem 3.1

For any $n,$ $lc\left(Q_n\right)=(n-1)2^{n-2}+1.$

Proof

Recall that the vertex set of $Q_n$ consists of the binary $n$-tuples and two vertices are adjacent, if their corresponding tuples differ in exactly one component. Let $A$ be the set of edges in $Q_n,$ whose both end vertices start with $0.$ While$B$ be the set of edges in $Q_n,$ whose both end vertices start with $1.$ For $1\le k\le (n-1)2^{n-2},$ the vertices corresponding to $A$ and $B$ in ${ℒ}_k\left(Q_n\right)$ are non-adjacent. So we call $A$ and $B$ to be “disjoint” subsets. Therefore, $lc\left(Q_n\right)\ge (n-1)2^{n-2}+1.$ We prove that $lc\left(Q_n\right)=(n-1)2^{n-2}+1=m.$

Suppose not. Then there exist two subsets $A$ and $B$ of $E\left(Q_n\right)$ each having $m$ elements such that they are disjoint. We have the following two cases.

(I). Suppose $n$ is odd.

We partition the $E\left(Q_n\right)$ into the following $(n+1)∕2$ spanning subgraphs.

Let $X_1$ be the set of rectangles created by varying the first two components of the binary $n$-tuples of $Q_n.$ $X_2$ be the set of rectangles created by varying third and fourth components, $X_3$ be the set of rectangles created by varying fifth and sixth components,…, $X_{(n-1)∕2}$ be the set of rectangles created by varying $(n-2)\text{th}$ and $(n-1)\text{st}$ components. $Y$ be the set of edges formed by varying the $n$th component of the binary $n$-tuples of $Q_n.$

It can be easily observed that $X_i$’s are all $2$-regular, spanning subgraphs of $Q_n,$ while $Y$ is a perfect matching.

Let $p=\frac{n+1}{2}.$

Then $\frac{m}{p}=\frac{(n-1)2^{n-2}+1}{(n+1)∕2}=\frac{n-1}{n+1}{2}^{n-1}+\frac{2}{n+1}.$

For $n\ge 3,$ we have $2^{n-2}+2^{n-4}\le \frac{m}{p}.$

Therefore, by Pigeonhole Principle, $A\cap X_1\ge 2^{n-2}+2^{n-4}$ and $B\cap X_p\ge 2^{n-2}+2^{n-4},$ $p\in 1,2,\dots ,(n-1)∕2,$ or $A\cap X_1\ge 2^{n-2}+2^{n-4}$ and $B\cap Y\ge 2^{n-2}+2^{n-4}.$

Case 1. $A\cap X_1\ge 2^{n-2}+2^{n-4}$ and $B\cap X_p\ge 2^{n-2}+2^{n-4},$ $p\in 1,2,\dots ,(n-1)∕2.$

Part (a). Assume that $(A\cap X_1)\cap (B\cap X_p)=\varphi .$

Now we try to prove the result for equality, as it is the minimal case. Suppose $A\cap X_1=2^{n-2}+2^{n-4}=B\cap X_p.$ If the edges in $A\cap X_1$ (similarly $B\cap X_p$) form rectangles, they need number of vertices equal to $2^{n-4}+2^{n-6}=5\cdot 2^{n-6},$ which is minimum. Similarly, if the edges form matching, they need $2^{n-1}+2^{n-3}-5\cdot 2^{n-3}$ vertices, which is maximum. Therefore, $2^{n-4}+2^{n-6}\le V(A\cap X_1),V(B\cap X_p)\le 2^{n-1}+2^{n-3}.$ Now we take different subcases according to the number of vertices required for $A\cap X_1$ and $B\cap X_p.$

Subcase (i). Suppose $V(A\cap X_1)=5\cdot 2^{n-6}=V(B\cap X_p).$ By Lemma 2.3, induced subgraph of $Q_n$ on $5\cdot 2^{n-6}$ vertices can have at the most $(5n-20)\cdot 2^{n-7}$ edges. Therefore $A$ can have at the most $(5n-20)\cdot 2^{n-7}$ edges on $V(A\cap X_1).$ Similarly, $B$ can have at the most $(5n-20)\cdot 2^{n-7}$ edges on $V(B\cap X_p).$ Now we are left with $2^n-5\cdot 2^{n-6}-5\cdot 2^{n-6}=2^{n-1}+2^{n-2}+2^{n-4}+2^{n-5}$ vertices. Again by Lemma 2.3, one can have at the most $(27n-15)\cdot 2^{n-6}$ edges in the induced subgraph on these vertices. But we need $2m-2\left[(2n-20)\cdot 2^{n-7}\right]=(27n-7)2^{n-6}+2$ more edges for the sets $A$ and $B,$ which is not possible.

Subcase (ii). Suppose $V(A\cap X_1)=5\cdot 2^{n-6},$ and $V(B\cap X_p)=5\cdot 2^{n-3}.$ By Lemma 2.3, $A$ can have at the most $(5n-20)\cdot 2^{n-7}$ edges on $V(A\cap X_1).$ While $B$ can have at the most $(40n-40)\cdot 2^{n-7}$ edges on $V(B\cap X_p).$ We are left with $2^n-5\cdot 2^{n-6}-5\cdot 2^{n-3}=2^{n-2}+2^{n-5}+2^{n-6}$ vertices. Again by Lemma 2.3, one can have at the most $(19n-40)\cdot 2^{n-7}$ edges in the induced subgraph on these vertices. But we need $2m-[(40n-40)\cdot 2^{n-7}+(5n-20)\cdot 2^{n-7}]=(19n-4)2^{n-7}+2$ more edges for the sets $A$ and $B,$ which is not possible.

Subcase (iii). Suppose $V(A\cap X_1)$ be the maximum possible, when $V(B\cap X_p)=5\cdot 2^{n-3}.$ Then $V(A\cap X_1)=3\cdot 2^{n-3}.$ By Lemma 2.3, $A$ can have at the most $(3n-5)\cdot 2^{n-4}$ edges on $V(A\cap X_1),$ and from above, $B$ can have at the most $(40n-40)\cdot 2^{n-7}=(5n-5)\cdot 2^{n-4}$ edges on $V(B\cap X_p).$ Note that all the vertices of $Q_n$ are exhausted by $V(A\cap X_1)$ and $V(B\cap X_p).$ But we still need $2m-[(3n-5)\cdot 2^{n-4}+(5n-5)\cdot 2^{n-4}]=2^{n-3}+2$ more edges, which is not possible.

Subcase (iv). $V(A\cap X_1)=V(B\cap X_p)=2^{n-1}+2^{n-3}.$ Note that this case is not possible, as it exceeds $2^n,$ the total number of vertices in $Q_n.$

It should be noted that, proving the result for the minimal cases is sufficient here. For, if we choose $A\cap X_1>2^{n-2}+2^{n-4}$ and $B\cap X_p>2^{n-2}+2^{n-4},$ $p\in 1,2,\dots ,(n-1)∕2,$ then obviously the number of vertices on which the edges are incident are more. This leads to an insufficient number of edges required for forming sets $A$ and $B$ which are disjoint.

Part (b). Suppose $(A\cap X_1)\cap (B\cap X_p)\ne \varphi .$ This is possible only for $p=1.$ So we have $(A\cap X_1)\cap (B\cap X_1)\ne \varphi .$ In this case also it suffices to assume only one common edge, as due to large number of common edges number of vertices available for the choice of remaining edges get reduced and one can easily get a contradiction. Also, we work out the subcase which is analogues to the Subcase (i) of the Part (I) only, as the remaining cases can be worked out in a similar manner.

Suppose $e\in (A\cap X_1)\cap (B\cap X_1).$ Then $(A\cap X_1)-e=2^{n-2}+2^{n-4}-1=(B\cap X_1)-e$ and hence, $V((A\cap X_1)-e)=5\cdot 2^{n-6}=V((B\cap X_1)-e).$ But again by the similar arguments as in the above case, we get a contradiction.

Case 2. $A\cap X_1\ge 2^{n-2}+2^{n-4}$ and $B\cap Y\ge 2^{n-2}+2^{n-4}.$

Again, we work out the minimal case only, i.e., the case of equality of both the quantities stated above.

Suppose $A\cap X_1=2^{n-2}+2^{n-4}=B\cap Y.$

Then $V(A\cap X_1)=2^{n-4}+2^{n-6}$ and $V(B\cap Y)=2^{n-1}+2^{n-3}.$ By Lemma 2.3, one can have at the most $(5n-20)2^{n-7}$ edges on an induced subgraph with $2^{n-4}+2^{n-6}$ vertices, while $(40n-40)2^{n-7}$ edges on the induced subgraph with $2^{n-1}+2^{n-3}$ vertices. Therefore, $A$ can have at the most $(5n-20)2^{n-7}$ edges on $V(A\cap X_1)$ and $B$ can have at the most $(40n-40)2^{n-7}$ edges on $V(B\cap Y).$ Now we are left with $2^n-(2^{n-4}+2^{n-6}+2^{n-1}+2^{n-3})=2^{n-2}+2^{n-5}+2^{n-6}$ vertices and the induced subgraph on these vertices can have at the most $(19n-40)2^{n-7}$ edges, by Lemma 2.3. But we need $2m-(5n-20)2^{n-7}-(40n-40)2^{n-7}=(19n-4)2^{n-7}+2$ more edges, which is not possible.

Therefore by Cases 1 and 2, it is clear that for odd $n,$ $lc\left(Q_n\right)=(n-1)2^{n-2}+1.$

(II). Suppose $n$ is even.

We partition the $E\left(Q_n\right)$ into the spanning subgraphs $X_1,X_2,\dots ,X_{n∕2},$ where $X_i$ is the set of rectangles created by varying $2i-1\text{st}$ and $2i\text{th}$ components, $i=1,2,\dots ,n∕2.$ So $p=\frac{n}{2}.$ The rest of the proof for this case follows on the similar lines as in (I).

Therefore, $lc\left(Q_n\right)=(n-1)2^{n-2}+1,$ for every $n.$ □

4 Concluding remark

Line completion numbers of hypercube variants can also be computed in a similar manner as above. So we have the following table.

Notes

Peer review under responsibility of Kalasalingam University.