On the genus of some total graphs

Abstract

Let $R$ be a commutative ring with a proper ideal $I$. A generalization of total graph is introduced and investigated. It is the (undirected) graph with all elements of $R$ as vertices, that two distinct vertices $x,y\in R$ are adjacent if and only if $x+y\in S_H\left(I\right)$ where $S_H\left(I\right)=\{a\in R:ra\in I$ for some $r\in H\}$ and $H$ is a multiplicatively closed subset of $R$. This version of total graph is denoted by $T\left({\Gamma }_H^I\left(R\right)\right)$. We in addition characterize certain lower and upper bounds for the genus of the total graph, and compute genus $T\left({\Gamma }_H^I\left(R\right)\right)$ on finite ring $R$, with respect to some special ideal $I$.

Keywords:

• Commutative rings
• Multiplicatively closed subset
• Total graph
• Genus

1 Introduction

Throughout, all rings will be commutative with non-zero identity. Let $R$ be a ring and $I$ a proper ideal of $R$. The $totalgraph$ of a commutative ring $R$, denoted by $T\left(\Gamma \left(R\right)\right)$, was introduced by Anderson and Badawi in [1] and studied by several authors ([2–4], etc.), where the authors in [3,4] obtained some facts on the genus of total graphs. They considered a total graph with all elements of $R$ as vertices, that two distinct vertices $x,y\in R$ are adjacent if and only if $x+y\in Z\left(R\right)$ where $Z\left(R\right)$ denotes the set of all zero-divisors of $R$. The total graph is then extended in joint papers [5,6] of the second author in rings and modules, respectively. Furthermore, a generalized total graph was introduced in [7]. For a proper submodule $N$ of $M$, there is a generalization of the graph of modules relative $N$ under multiplicatively closed subset $H$ denoted by $T\left({\Gamma }_H^N\left(M\right)\right)$ which was studied by present authors in [8]. The vertex set of $T\left({\Gamma }_H^N\left(M\right)\right)$ is $M$, that two distinct vertices $m$ and $m^{\prime }$ are adjacent if and only if $m+m^{\prime }\in M_H\left(N\right)$ where $M_H\left(N\right)=\{m\in M:rm\in N$ for some $r\in H\}$ and $H$ is a multiplicatively closed subset of $R$, i.e. $ab\in H$ for all $a,b\in H$. As $N$ is a proper submodule of $M$ and $N\subseteq M_H\left(N\right)$, $M_H\left(N\right)$ is not empty.

We define a generalized total graph over ring $R$, denoted by $T\left({\Gamma }_H^I\left(R\right)\right)$, with all elements of $R$ as vertices, that two distinct vertices $x,y\in R$ are adjacent if and only if $x+y\in S_H\left(I\right)$ where $S_H\left(I\right)=\{a\in R:ra\in I$ for some $r\in H\}$, $I$ is an ideal of $R$ and $H$ is a multiplicatively closed subset of $R$.

It follows from the definition that if $S_H\left(I\right)=R$, (for example, if $I=R$, $0\in H$, $H\bigcap (S_H\left(I\right):R)\ne \varnothing$, $H\bigcap (0:R)\ne \varnothing$ or $H\bigcap (I:R)\ne \varnothing$, by [8]), then $T\left({\Gamma }_H^I\left(R\right)\right)$ is complete; so we suppose that $S_H\left(I\right)\ne R$. We denote by ${\Gamma }_H^I\left(S_H\left(I\right)\right)$ and ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ the (induced) subgraphs of $T\left({\Gamma }_H^I\left(R\right)\right)$ with vertices in $S_H\left(I\right)$ and $R-S_H\left(I\right)$, respectively. Based on our assumption, $S_H\left(I\right)\ne R$ and so ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is always nontrivial.

Let $G$ be a simple graph. We say that $G$ is $totallydisconnected$ if none of two vertices of $G$ are adjacent. We use $K_n$ to denote complete graph with $n$ vertices. A $bipartitegraph$ $G$ is a graph whose vertex set $V\left(G\right)$ can be partitioned into subsets $V_1$ and $V_2$ such that the edge set consists of precisely those edges which join vertices in $V_1$ to vertices of $V_2$. In particular, if $E$ consists of all possible such edges, then $G$ is called the $completebipartitegraph$ and denoted by $K_{m,n}$ when $\left|V_1\right|=m$ and $\left|V_2\right|=n$. Two subgraphs $G_1$ and $G_2$ of $G$ are $disjoint$ if $G_1$ and $G_2$ have no common vertices and no vertex of $G_1$ (resp., $G_2$) is adjacent (in $G$) to any vertex not in $G_1$ (resp., $G_2$). The $union$ of two graphs $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ is the graph $G_1\cup G_2$ whose vertex set is $V_1\cup V_2$ and the edge set is $E_1\cup E_2$. The $Cartesianproduct$ of graphs $G_1$ and $G_2$ is defined as the graph $G_1\times G_2$ which the vertex set is $V\left(G_1\right)\times V\left(G_2\right)$ and the edge set is the set of all pairs $(u_1,v_1)(u_2,v_2)$ such that either $u_1{u}_2\in E\left(G_1\right)$ and $v_1=v_2$ or $v_1{v}_2\in E\left(G_2\right)$ and $u_1=u_2$. Two graphs $G$ and $H$ are said to be $isomorphic$ to each another, written $G\cong H$, if there exists a bijection $f:V\left(G\right)\to V\left(H\right)$ such that for each pair $x,y$ of vertices of $G$, $xy\in E\left(G\right)$ if and only if $f\left(x\right)f\left(y\right)\in E\left(H\right)$. For a vertex $v$ of graph $G$, $deg\left(v\right)$ is the degree of vertex $v$ and $\delta \left(G\right)≔min\{deg\left(v\right)$: $v$ is a vertex of $G\}$. For a nonnegative integer $k$, a graph $G$ is called $k-regular$ if every vertex of $G$ has degree $k$. The $genus$ of a graph $G$, denoted by $g\left(G\right)$, is the minimal integer $n$ such that the graph can be embedded in $S_n$, where $S_n$ denotes a sphere with $n$ handles. Intuitively, $G$ is embedded in a surface if it can be drawn in the surface so that its edges intersect only at their common vertices. A $planargraph$ is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. For such graphs the genus is zero. A graph with genus one is called a $toroidal$ graph. If $G^{\prime }$ is a subgraph of $G$, then $g\left(G^{\prime }\right)\le g\left(G\right)$. For details on the notion of embedding of a graph in a surface, see White [9, Chapter 6].

In Section 2, we remind some facts and give a lower bound for genus of the graph $T\left({\Gamma }_H^I\left(R\right)\right)$. We proceed in Section 3 by determining all isomorphism classes of finite rings $R$ whose $T\left({\Gamma }_H^I\left(R\right)\right)$ has genus at most one (i.e. a planar or toroidal graph). Also, we compute genus of the graph over $R={\mathbb{Z}}_n$ under some well-known multiplicatively closed subsets of $R$.

2 Background problem and some comments

Throughout, $\lceil x\rceil$ denotes the least integer that is greater than or equal to $x$. In the following theorem we give some well-known formulas, see, e.g., [9–11]:

Theorem 2.1

The following statements hold:

(1)	For $n\ge 3$ we have $g\left(K_n\right)=\lceil \frac{(n-3)(n-4)}{12}\rceil$.
(2)	For $m,n\ge 2$ we have $g\left(K_{\stackrel{}{m,n}}\right)=\lceil \frac{(m-2)(n-2)}{4}\rceil$.
(3)	Let $G_1$ and $G_2$ be two graphs and for each $i,p_i$ be the number of vertices of $G_i$. Then max $\{p_{1}g\left(G_2\right)+g\left(G_1\right),p_{2}g\left(G_1\right)+g\left(G_2\right)\}\le g(G_1\times G_2)$.
(4)	The genus of a graph is the sum of the genuses of its components.

According to Theorem 2.1 we have $g\left(K_n\right)=0$ for $1\le n\le 4$, $g\left(K_n\right)=1$ for $5\le n\le 7$ and $g\left(K_n\right)\ge 2$, for other value of $n$.

Corollary 2.2

If $G$ is a graph with $n$ vertices, then $g\left(G\right)\le \lceil \frac{(n-3)(n-4)}{12}\rceil$.

In the following of the section, we characterize a lower bound for the genus of the graph $T\left({\Gamma }_H^I\left(R\right)\right)$. Considering the fact that ${\Gamma }_H^I\left(S_H\left(I\right)\right)$ is in the form of $K_{\left|S_H\left(I\right)\right|}$ (see [8, Remark 3.1]), in view of Theorem 2.1, it is enough for us to obtain a lower bound for genus of the graph ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$.

Theorem 2.3

[8, Corollary 3.7] Let $\mid S_H\left(I\right)\mid =\alpha$, $\mid R∕S_H\left(I\right)\mid =\beta$, and $2\in (S_H\left(I\right):R)$.Then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\beta -1$ copies of $K_{\alpha }$.

Theorem 2.4

[8, Theorem 3.10] Let $\mid S_H\left(I\right)\mid =\alpha$ and $\mid R∕S_H\left(I\right)\mid =\beta$. If $H$, a multiplicatively closed subset of $R$ containing some even elements, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{\beta -1}{2}$ copies of $K_{\alpha ,\alpha }$.

Corollary 2.5

Let $\left|S_H\left(I\right)\right|=\alpha$ and $|R∕S_H\left(I\right)|=\beta$. Then the following hold:

1.	If $2\in (S_H\left(I\right):R)$, then $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=(\beta -1)\lceil \frac{(\alpha -3)(\alpha -4)}{12}\rceil$.
2.	If $2r\in H$ for some $r\in R$, then $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{\beta -1}{2}\lceil \frac{{(\alpha -2)}^2}{4}\rceil$ .

Proof

It is obvious by Theorems 2.3 and 2.4.

Lemma 2.6

[12 , Proposition .2.1] If $G$ is a graph with $n$ vertices and genus $g$, then $\delta \left(G\right)\le 6+\frac{12g-12}{n}$.

Theorem 2.7

[8 , Theorem 3.13] Suppose that the edge set of ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is not empty and $x$ is a vertex of the graph. Then the degree of $x$ is either $\mid S_H\left(I\right)\mid$ or $\mid S_H\left(I\right)\mid -1$.

Proposition 2.8

Let ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ with $t^{\prime }$ vertices have a nonempty edge set, and let $\left|S_H\left(I\right)\right|=t$. Then $\frac{(t-7)t^{\prime }}{12}+1\le g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)$.

Proof

By Lemma 2.6 and Theorem 2.7, $t-1=\left|S_H\left(I\right)\right|-1=\delta$, so $t-1\le 6+\frac{(12g-12)}{t^{\prime }}$. Then $(t-7)t^{\prime }\le 12g-12$. Hence $\frac{(t-7)t^{\prime }}{12}+1\le g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)$.

Corollary 2.9

If $R$ is infinite, then $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)$is infinite for all ideals $I$ and all closed subsets $H$ of $R$.

3 The genus of $T\left({\Gamma }_H^I\left(R\right)\right)$

Considering Corollary 2.9, the genus will be infinite if $R$ is not a finite ring. In order to compute the genus, we consider a finite ring $R$.

In view of Theorem 2.1, it is enough for us to study the genus of ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$.

Remark 3.1

If $H\cap I\ne \varnothing$, then $S_H\left(I\right)=R$ and ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is trivial so, in the following, we suppose that $H\cap I=\varnothing$. It should be noted that if $H\cap I=\varnothing$, then $H\cap S_H\left(I\right)=\varnothing$.

Theorem 3.2

Let $R$ be a finite ring such that $R=R_1\times R_2\times \cdots \times R_t$ with $t\ge 4$, $I=0\times R_2\times \cdots \times R_t$ and $H$ be a multiplicatively closed subset of $R$. Then $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\ge 2$.

Proof

It is enough to show that there is a subgraph $L$ of ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ with $\gamma \left(L\right)\ge 2$; this implies that $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\ge 2$. So, we proceed for $t=4$.

1.

Let $H\cap (Z\left(R_1\right)\times R_2\times \cdots \times R_t)=\varnothing$. Then $I=S_H\left(I\right)$. By way of contradiction, let there exists $(r_1,\dots ,r_t)\in R-I$ such that $(r_1,\dots ,r_t)(h_1,\dots ,h_t)\in I$ for some $(h_1,\dots ,h_t)\in H$ (note that $h_1$ has inverse in $R_1$). Then $r_1{h}_1=0$ implies that $r_1=0$, a contradiction. $\left(1^{\prime }\right)$ If $R_1={\mathbb{Z}}_2$, then $K_8\subseteq {\Gamma }_H^I\left(S_H^C\left(I\right)\right)$. $\left(2^{\prime }\right)$ Let $\left|R_1\right|>2$. $\left(a^{\prime }\right)$ If $2\in Z\left(R_1\right)$, then considering the vertices $\left\{(a_1,a_2,a_3,a_4)\right|a_i\in R_i$ for $i\ge 2\}$, there is $a_1\ne 0$ belonging to $R_1$ such that $2a_1=0$. So, $K_8\subseteq {\Gamma }_H^I\left(S_H^C\left(I\right)\right)$. $\left(b^{\prime }\right)$. Let $2\notin Z\left(R_1\right)$. For a non zero element $l_1\in R_1$, set $X_1=\{(l_1,l_2,l_3,l_4)\in R|l_i\in R_i$ for $2\le i\le 4\}$ and $Y_1=\{(-l_1,l_2,l_3,l_4)\in R|l_i\in R_i$ for $2\le i\le 4\}$. Then $X_1,Y_1$ is a bipartition for $K_{n,n}$ for $n\ge 8$. Hence, $K_8\subseteq {\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ or $K_{8,8}\subseteq {\Gamma }_H^I\left(S_H^C\left(I\right)\right)$; so $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\ge 2$.

2.

Let $H\cap (Z\left(R_1\right)\times R_2\times \cdots \times R_t)\ne \varnothing$. Set $T=H\cap (Z\left(R_1\right)\times R_2\times \cdots \times R_t)$. For $(d_1,d_2,\dots ,d_t)\in T$, put $K_{(d_1,d_2,\dots ,d_t)}=\{(b_1,b_2,\dots ,b_t)\in R|b_1\ne 0,b_1{d}_1=0\}$ and define $K={\bigcup }_{(d_1,d_2,\dots ,d_t)\in T}{K}_{(d_1,d_2,\dots ,d_t)}$. Claim. $S_H\left(I\right)=I\cup K$. Let there exists $(r_1,\dots ,r_t)\in R-I$ such that $(r_1,\dots ,r_t)(h_1,\dots ,h_t)\in I$ for some $(h_1,\dots ,h_t)\in H$. Then $r_1{h}_1=0$ implies that $h_1\in Z\left(R_1\right)-\left\{0\right\}$ (by $I\cap H=\varnothing$). So $(r_1,\dots ,r_t)\in K$. Conversely, let $(b_1,n_2,\dots ,n_t)\in K$. Then there exists $(d^{\prime },n^{\prime }{}_2...,n^{\prime }{}_t)\in T$ such that $b_1{d}^{\prime }=0$. So $(b_1,n_2,\dots ,n_t)(d^{\prime },n^{\prime }{}_2...,n^{\prime }{}_t)\in I$ implies that $(b_1,n_2,\dots ,n_t)\in S_H\left(I\right)$, hence $K\subseteq S_H\left(I\right)$. Therefore, $S_H\left(I\right)=I\cup K$. (i) If $R_1={\mathbb{Z}}_2$, then $K_8\subseteq {\Gamma }_H^I\left(S_H^C\left(I\right)\right)$. (ii) Suppose $\left|R_1\right|>2$. (${\mathrm{i}}^{\prime }$) Let there exists $(2,m_2,m_3,m_4)\in T_4$, where $T_4=H\cap (Z\left(R_1\right)\times R_2\times R_3\times R_4)$. Then $2\in Z\left(R_1\right)-\left\{0\right\}$ (by $H\cap I=\varnothing$). So $2a_1=0$ for non zero element $a_1\in R_1$ and $\left\{(a_1,n_2,n_3,n_4)\right|n_i\in R_i$ for $2\le i\le 4\}\subseteq K\subseteq S_H\left(I\right)$, then $a_1\ne 2$ (otherwise, $S_H\left(I\right)\cap H\ne \varnothing$), also $a_1\ne 1$ since $2\ne 0$ (by $I\cap H=\varnothing$). Considering distinct sets $\left\{(a_1-1,a_2,a_3,a_4)\right|a_i\in R_i$ for $i\ge 2\}$, one has $K_{8,8}\subseteq {\Gamma }_H^I\left(S_H^C\left(I\right)\right)$. (${\mathrm{ii}}^{\prime }$) Let $(2,m_2,m_3,m_4)\notin T_4$ for every $m_i\in R_i$ with $i\ge 2$. By the similar argument of case 1., if $2\in Z\left(R_1\right)$, then $K_8\subseteq {\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ and if $2\notin Z\left(R_1\right)$, then $K_{8,8}\subseteq {\Gamma }_H^I\left(S_H^C\left(I\right)\right)$. Hence, $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\ge 2$.

Remark 3.3

It should be noted that, Theorem 3.2 is satisfied for every $I=R_1\times R_2\times \cdots \times R_{n-1}\times 0\times R_{n+1}\times \cdots \times R_t$ with $n>1$ and $t\ge 4$.

Theorem 3.4

Let $R=R_1\times R_2\times R_3$ where every $R_i$ is a finite ring for $1\le i\le 3$, $I=0\times R_2\times R_3$ and $H$ be a multiplicatively closed subset of $R$.

1.

Let $H\cap (Z\left(R_1\right)\times R_2\times R_3)=\varnothing$or $H\cap (Z\left(R_1\right)\times R_2\times R_3)\ne \varnothing$ with $(2,m_2,m_3)\notin H\cap (Z\left(R_1\right)\times R_2\times R_3)$ for every $m_2\in R_2$ and $m_3\in R_3$. (i) If $2\in Z\left(R_1\right)$ and $\left|R_2\right|\left|R_3\right|\ge 8$, then $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\ge 2$. (ii) If $2\notin Z\left(R_1\right)$ and $\left|R_2\right|\left|R_3\right|\ge 4$, then $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\ge 1$.

2.

Let there exists $(2,m_2,m_3)\in H\cap (Z\left(R_1\right)\times R_2\times R_3)$ and $\left|R_2\right|\left|R_3\right|\ge 4$. Then $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\ge 1$.

Proof

1.

(i) Consider $\left\{(a_1,a_2,a_3)\right|a_i\in R_i\}$ which is in the form of $K_n$ for $n\ge 8$, where $2a_1=0$ for some $a_1\ne 0$ belonging to $R_1$. (ii) For a non zero element $l_1\in R_1$, consider $\{(l_1,l_2,l_3)|l_i\in R_i,i=2,3\}\cup \left\{(-l_1,m_2,m_3)\right|m_i\in R_i,i=2,3\}$ which is in the form of $K_{n,n}$ for $n\ge 4$.

2.

If there is $(2,m_2,m_3)\in H\cap (Z\left(R_1\right)\times R_2\times R_3)$, then $2\in Z\left(R_1\right)-\left\{0\right\}$, so $2a_1=0$ for non zero element $a_1\in R_1$ and $\left\{(a_1,n_2,n_3)\right|n_i\in R_i,i=2,3\}\subseteq S_H\left(I\right)$, then $a_1\ne 2$ (otherwise, $S_H\left(I\right)\cap H\ne \varnothing$); furthermore, $a_1\ne 1$ since $2\ne 0$ ( by $I\cap H=\varnothing$). Hence the vertices $\left\{(a_1-1,a_2,a_3)\right|a_i\in R_i,i=2,3\}\cup \left\{(1,a_2,a_3)\right|a_i\in R_i,i=2,3\}$ are in the form of $K_{n,n}$ for $n\ge 4$.

Corollary 3.5

Let $R=R_1\times R_2$ where every $R_i$ is a finite ring for $i\in \{1,2\}$, $I=0\times R_2$ and $H$ be a multiplicatively closed subset of $R$.

It is easily proved that the following statements hold.

1.

Let $H\cap (Z\left(R_1\right)\times R_2)=\varnothing$or $H\cap (Z\left(R_1\right)\times R_2)\ne \varnothing$ with $(2,m_2)\notin H\cap (Z\left(R_1\right)\times R_2)$ for every $m_2\in R_2$. (i) If $2\in Z\left(R_1\right)$ and $\left|R_2\right|\ge 8$, then $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\ge 2$. (ii) If $2\notin Z\left(R_1\right)$ and $\left|R_2\right|\ge 4$, then $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\ge 1$.

2.

Let there exists $(2,m_2)\in H\cap (Z\left(R_1\right)\times R_2)$ and $\left|R_2\right|\ge 4$. Then $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\ge 1$.

Proof

It is obvious by Theorem 3.4.

Example 3.6

Let $R={\mathbb{Z}}_6\times {\mathbb{Z}}_4$, $I=0\times {\mathbb{Z}}_4$ and $H$ be a multiplicatively closed subset of $R$. Then $Z\left(R\right)=(Z\left({\mathbb{Z}}_6\right)\times {\mathbb{Z}}_4)\cup ({\mathbb{Z}}_6\times Z\left({\mathbb{Z}}_4\right))$. If $H\cap (Z\left({\mathbb{Z}}_6\right)\times {\mathbb{Z}}_4)=\varnothing$, then $S_H\left(I\right)=I$. Let $H\cap (Z\left({\mathbb{Z}}_6\right)\times {\mathbb{Z}}_4)\ne \varnothing$ and let $(2,n_s)\in H$ (so for every $n_i\in {\mathbb{Z}}_4$, $(3,n_i)\notin H$, otherwise $H\cap I\ne \varnothing$). Then $S_H\left(I\right)=I\cup \left\{(3,t_2)\right|t_2\in {\mathbb{Z}}_4\}$. Considering the vertices of ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ in the form of $\{(1,b_2),(4,t_2)|b_2,t_2\in {\mathbb{Z}}_4\}\cup \{(2,m_2),(5,l_2)|m_2,l_2\in {\mathbb{Z}}_4\}$, one has ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a $K_{8,8}$.

Theorem 3.7

Let $R={\mathbb{F}}_q\times R_n$, $I=0\times R_n$ where $R_n$ is a ring with $\left|R_n\right|=n$, ${\mathbb{F}}_q$ is a field with $q$ elements and let $H$ be a multiplicatively closed subset of $R$.

1.	Let $q=2^m$.Then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is planar if and only if $2\le n\le 4$ and it is toroidal if and only if $m=1$ and $5\le n\le 7$.
2.	If for every $m\in \mathbb{N}$, $q\ne 2^m$, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is planar if and only if $n=2$ and it is toroidal if and only if $q=3$ and $n\in \{3,4\}$.

Proof

Claim; for every $n\in \mathbb{N}$, $I=S_H\left(I\right)$. By way of contradiction, let there exists $(m,d)\in R-I$ such that $(m,d)(t,l)\in I$ for some $(t,l)\in H$. So $mt=0$ which implies that $m=0$; so $m=0$, a contradiction.

1.

Let $q=2^m$. (a) If $m=1$, for every $(1,b)\in S_H^C\left(I\right)$, we have $(1,b)+(1,b^{\prime })\in S_H\left(I\right)$ where $b,b^{\prime }$ are disjoint elements of $R_n$. So ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is $K_n$. (b) Let $m>1$. Considering vertices of ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ in the form of $\left\{(l,a)\right|l\in {\mathbb{F}}_{2^m},a\in R_n\}$ and by the fact that $char\left({\mathbb{F}}_{2^m}\right)=2$, in the same way of proof of Theorem 3.2, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $2^m-1$ copies of $K_n$. Hence, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is planar if and only if $2\le n\le 4$ and it is toroidal if and only if $m=1$ and $5\le n\le 7$.

2.

Let for all $m\in \mathbb{N}$, one has $q\ne 2^m$. For non zero element $l\in F_q$, let $X_l=\left\{(l,a)\right|a\in R_n\}$ and $Y_l=\left\{(-l,a)\right|a\in R_n\}$. Then $X_l,Y_l$ is a bipartition of $K_{n,n}$. So ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{q-1}{2}$ copies of $K_{n,n}$. Hence ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is planar if and only if $n=2$ and it is toroidal if and only if $q=3$ and $n\in \{3,4\}$.

Theorem 3.8

Let $R$ be a finite ring for which $R=R_1\times R_2\times \cdots \times R_t$ with $t\ge 2$, $I=0\times R_2\times \cdots \times R_t$, $H=R-Z\left(R\right)$ and let $2\notin Z\left(R_1\right)$. If $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\le 1$, then $R$ is isomorphic to the one of the following rings: $${\mathbb{Z}}_3\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2,R_1\times {\mathbb{Z}}_2,{\mathbb{Z}}_3\times {\mathbb{Z}}_3,{\mathbb{Z}}_3\times {\mathbb{Z}}_4,{\mathbb{Z}}_3\times {\mathbb{F}}_4,{\mathbb{Z}}_3\times {\mathbb{Z}}_2\left[X\right]∕\left(X^2\right).$$

Proof

Note that $t<4$, by Theorem 3.2.

1′.

Let $t=3$. If $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)<1$, then $\left|R_2\right|\left|R_3\right|<4$, by Theorem 3.4. For $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=1$, consider $\left|R_2\right|\left|R_3\right|=4$, by the proof of Theorem 3.4. So, for $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\le 1$, $\left|R_2\right|\left|R_3\right|\le 4$. Hence $R_2=R_3={\mathbb{Z}}_2$. For every non zero element $b_1\in R_1$, set $X_{b_1}=\left\{(b_1,n_2,n_3)\right|n_i\in R_i,i=2,3\}$. Then $X_{b_1},X_{-b_1}$ is a bipartition of $K_{4,4}$. If $\left|R_1\right|>3$, then $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\ge 2$ (since there exist at least two bipartition of $K_{4,4}$ in ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ ). Hence, $\left|R_1\right|\le 3$, so $R_1={\mathbb{Z}}_3$ (since $2\notin Z\left(R_1\right)$). Therefore, $R={\mathbb{Z}}_3\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$.

2′.

Let $t=2$. For every non zero element $b_1\in R_1$, set $X_{b_1}=\left\{(b_1,n_2)\right|n_2\in R_2\}$. Then $X_{b_1},X_{-b_1}$ is a bipartition of $K_{n,n}$ for $n=\left|R_2\right|$. Since $2\notin Z\left(R_1\right)$ and $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\le 1$, then by Corollary 3.5 and by the same way of case $1^{\prime }$, $\left|R_2\right|\le 4$. (i) Let $\left|R_2\right|=2$. Then $X_{b_1}$ and $X_{-b_1}$, for nonzero $b_1\in R_1,$ are in the form of $K_{2,2}$ and ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of some copies of $K_{2,2}$. So for every $R=R_1\times R_2$ with $\left|R_2\right|=2$, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is planar. (ii) Let $\left|R_2\right|=3,4$. For every non zero element $b_1\in R_1$, $X_{b_1},X_{-b_1}$ is a bipartition of $K_{3,3}$ or $K_{4,4}$ and $\gamma \left(K_{3,3}\right)=\gamma \left(K_{4,4}\right)=1$. So, by $2\notin Z\left(R_1\right)$ and the same way of case $1^{\prime }$, $\left|R_1\right|=3$ and $R_1={\mathbb{Z}}_3$. Hence, for $t=2$, $R$ is isomorphic to the one of the following rings: $$R_1\times {\mathbb{Z}}_2,{\mathbb{Z}}_3\times {\mathbb{Z}}_3,{\mathbb{Z}}_3\times {\mathbb{Z}}_4,{\mathbb{Z}}_3\times {\mathbb{F}}_4,{\mathbb{Z}}_3\times {\mathbb{Z}}_2\left[X\right]∕\left(X^2\right).\square$$

Proposition 3.9

Let $R$ be a finite ring for which $R=R_1\times R_2\times \cdots \times R_t$ with $t\ge 2$, $I=0\times R_2\times \cdots \times R_t$, $H=R-Z\left(R\right)$ and let $2\in Z\left(R_1\right)$. If $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\le 1$, then $R$ is isomorphic to the one of the following rings: $$R_1\times {\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_5,{\mathbb{Z}}_2\times {\mathbb{Z}}_6,{\mathbb{Z}}_2\times {\mathbb{Z}}_7,\text{or}{R}_1\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2,R_1\times {\mathbb{Z}}_3,R_1\times R_{2}with\left|R_2\right|=4.$$

Proof

Note that $t<4$, by Theorem 3.2. Put $P=\{a_1\in R_1|a_1\ne 0,2a_1=0\}(\left|P\right|\ge 1$, by $2\in Z\left(R_1\right)$) and ${R_1}^{\star }=R_1-\left\{0\right\}$.

1.

Let $t=3$. Put $l=\left|R_2\right|\left|R_3\right|$. For every non zero element $a_1\in R_1$, set $X_{a_1}=\left\{(a_1,n_2,n_3)\right|n_i\in R_i,i=2,3\}$. If $a_1\in P$, then $X_{a_1}$ is in the form of $K_l$. If $a_1\notin P$, then $X_{a_1},X_{-a_1}$ is a bipartition of $K_{l,l}$. Since $2\in Z\left(R_1\right)$, then by Theorem 3.4, $\left|R_2\right|\left|R_3\right|<8$. So $\left|R_2\right|\left|R_3\right|=4$ or $6$. (a) Let $\left|R_2\right|\left|R_3\right|=4$. (${\mathrm{i}}^{\prime }$) If $char\left(R_1\right)=2$ ($R_1^{\star }=P$), then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of some copies of $K_4$, which is planar. (${\mathrm{ii}}^{\prime }$) Let $char\left(R_1\right)\ne 2$. Consider $\overline{P}={R_1}^{\star }-P$ (note that $\left|\overline{P}\right|\ge 2$). Suppose that $\left|\overline{P}\right|>2$. We claim that $\left|\overline{P}\right|\ge 4$. If $\left|\overline{P}\right|=3$ and $a_1,-a_1,a_2\in \overline{P}$, then $-a_2\in \overline{P}$. So $\left|\overline{P}\right|=4$, a contradiction. Hence, if $\left|\overline{P}\right|>2$, considering the sets $X_{a_1},X_{-a_1}$ and $X_{a_2},X_{-a_2}$ where $a_1,-a_1,a_2,-a_2\in \overline{P}$, there are at least two copies of $K_{4,4}$ in ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ that implies, $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\ge 2$. So, $\left|\overline{P}\right|=2$. Then for $b_1,-b_1\in \overline{P}$, $X_{b_1},X_{-b_1}$ is in the form of $K_{4,4}$. Thus, in this case, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of some copies of $K_4$ and one copy of $K_{4,4}$, which is toroidal. Therefore, if $t=3$ and $\left|R_2\right|\left|R_3\right|=4$, then $R=R_1\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$ with $char\left(R_1\right)=2$ ($R_1^{\star }=P$) or $\left|\overline{P}\right|=2$. (b) Let $\left|R_2\right|\left|R_3\right|=6$. If $char\left(R_1\right)\ne 2$, then $K_{6,6}$ is a subgraph of ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ which implies that $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)>1$. So $char\left(R_1\right)=2$. Also, by $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\le 1$, we should have $\left|P\right|=1$, since for every $l\in P$, $K_6\subseteq {\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ and $\gamma \left(K_6\right)=1$. Hence, in this case we have $R_1=Z_2$ and $R$ is isomorphic to ${\mathbb{Z}}_2\times {\mathbb{Z}}_6.$

2.

Let $t=2$. For every non zero element $a_1\in R_1$, set $X_{a_1}=\left\{(a_1,n_2)\right|n_2\in R_2\}$. Since $2\in Z\left(R_1\right)$, then by Corollary 3.5, $n=\left|R_2\right|<8$. For every non zero element $a_1\in P$, $X_{a_1}$ is in the form of $K_n$ for $n\le 7$. If $a_1\notin P$, then $X_{a_1},X_{-a_1}$ is a bipartition of $K_{n,n}$. ($a^{\prime }$) Let $\left|R_2\right|=2.$ If $char\left(R_1\right)=2$, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of some copies of $K_2$, which is planar. If $char\left(R_1\right)\ne 2$ ($R_1^{\star }\ne P$), then for every $a_1\in \overline{P}$, $X_{a_1},X_{-a_1}$ is a bipartition of $K_{2,2}$. So ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of some copies of $K_2$ and $K_{2,2}$, which is planar. Hence, in this case, $R=R_1\times {\mathbb{Z}}_2$. ($b^{\prime }$) Let $\left|R_2\right|=3$. If $char\left(R_1\right)=2$, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of some copies of $K_3$, which is planar. Let $char\left(R_1\right)\ne 2$ ($R_1^{\star }\ne P$). If $\left|\overline{P}\right|>2$, then $\left|\overline{P}\right|\ge 4$. So, there exist at least two copies of $K_{3,3}$ in ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ that implies that ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)\ge 2$. Hence, $\left|\overline{P}\right|=2$ and ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of some copies of $K_3$ and one copy of $K_{3,3}$, which is toroidal. Thus, in this case, $R=R_1\times {\mathbb{Z}}_3$ with $char\left(R_1\right)=2$ or $\left|\overline{P}\right|=2$. ($c^{\prime }$) If $\left|R_2\right|=4$, then by the same way of case 1(a), $R=R_1\times R_2$, where $\left|R_2\right|=4$ with $char\left(R_1\right)=2$ or $\left|\overline{P}\right|=2$. ($d^{\prime }$). Let $\left|R_2\right|\in \{5,6,7\}$. If $\left|P\right|\ge 2$, then $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\ge 2$ ( since for every $a_1\in P$, $K_n\subseteq {\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ for $n\in \{5,6,7\}$). So $\left|P\right|=1$. If $char\left(R_1\right)\ne 2$, then $K_{n,n}\subseteq {\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ for $n\in \{5,6,7\}$, that implies that $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)>1$. So $char\left(R_1\right)=2$ and $R_1={\mathbb{Z}}_2$, since $\left|P\right|=1$. Hence, in this case, $R$ is isomorphic to the one of the following rings: $${\mathbb{Z}}_2\times {\mathbb{Z}}_5,{\mathbb{Z}}_2\times {\mathbb{Z}}_6,{\mathbb{Z}}_2\times {\mathbb{Z}}_7.\square$$

Remark 3.10

Let $R$ be a ring with $I=0$ and $H$ be a multiplicatively closed subset of $R$. Then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a subgraph of $T\left(\Gamma \left(R\right)\right)$, since $S_H\left(I\right)=\{r\in R:rs=0$ for some $s\in H(0\notin H)\}\subseteq Z\left(R\right)$. Recall that $T\left(\Gamma \left(R\right)\right)$ is the graph with all elements of $R$ as vertices, and two distinct vertices $x,y\in R$ are adjacent if and only if $x+y\in Z\left(R\right)$ where $Z\left(R\right)$ denotes the set of all zero-divisors of $R$, so $\gamma \left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)\le \gamma \left(T\left(\Gamma \left(R\right)\right)\right)$.

For finite ring $R$ with ideal $I=0\times 0\times \cdots \times R_n\times \cdots \times R_t$, $n\ge 1,t\ge 2$ and multiplicatively closed subset $H$ of $R$, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a subgraph of $T\left(\Gamma \left(R\right)\right)$, since $S_H\left(I\right)\subseteq Z\left(R\right)$. For the recent inclusion, let $(r_1,r_2,\dots ,r_t)\in S_H\left(I\right)$. Then $(r_1,r_2,\dots ,r_t)(s_1,s_2,\dots ,s_t)\in I$ for some $(s_1,s_2,\dots ,s_t)\in H$, so $r_i{s}_i=0$ for every $1\le i\le n-1$. If for every $1\le i\le n-1$, $s_i=0$, then $H\cap I\ne \varnothing$, a contradiction, so there exists $s_l\ne 0$ for $1\le l\le n-1$. Then $r_l{s}_l=0$ implies that $r_l\in Z\left(R_l\right)$, hence $S_H\left(I\right)\subseteq Z\left(R\right)$.

Theorem 3.11

Let $I=k{\mathbb{Z}}_n$ with $d=(k,n)$ and $H=\left\{a\right|a\in {\mathbb{Z}}_n,(a,n)=1\}$.

1.

Let $n$ be an even integer. (i) If $d$ is an even integer, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $K^{\frac{n}{d}}$ and $\frac{d-2}{2}$ copies of $K_{\frac{n}{d},\frac{n}{d}}$. Hence $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\lceil \frac{(\frac{n}{d}-3)(\frac{n}{d}-4)}{12}\rceil +\frac{d-2}{2}\lceil \frac{{(\frac{n}{d}-2)}^2}{4}\rceil$. (ii) If $d$ is an odd integer, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{d-1}{2}$ copies of $K_{\frac{n}{d},\frac{n}{d}}$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{d-1}{2}\lceil \frac{{(\frac{n}{d}-2)}^2}{4}\rceil$.

2.

If $n$ is an odd integer, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{d-1}{2}$ copies of $K_{\frac{n}{d},\frac{n}{d}}$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{d-1}{2}\lceil \frac{{(\frac{n}{d}-2)}^2}{4}\rceil$.

Proof

We at first show that $d{\mathbb{Z}}_n=I=S_H\left(I\right)$. There are $t_1,t_2\in \mathbb{Z}$ such that $t_{1}n+t_{2}k=d$, so $d\in I$. Hence $I=d{\mathbb{Z}}_n$. We claim that $I=S_H\left(I\right)$. By way of contradiction, if there exists $m\in {\mathbb{Z}}_n-I$ such that $tm\in I$ for some $t\in H$, then $d|tm$. But $(d,t)=1$ ( since $d|n$), so $d|m$, a contradiction. Hence $I=S_H\left(I\right).$

1.

Let $n$ be an even integer. Then (i) If $d=2$, then $I=2{\mathbb{Z}}_n$; so for every $m^{\prime }\in S_H^C\left(I\right)$, $2m^{\prime }\in S_H\left(I\right)$. Then by Theorem 2.3, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is in the form of $K_{\frac{n}{2}}$. Therefore, $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\lceil \frac{(\frac{n}{2}-3)(\frac{n}{2}-4)}{12}\rceil$, by Theorem 2.1. Let $d$ be an even integer greater than $2$, then $S_H^C\left(I\right)$ has the following elements: $1,2,\dots ,\frac{d}{2},\dots ,d-1$ $d+1,\dots ,\frac{3d}{2},\dots ,2d-1$ . . . $\left[(\frac{n}{d}-1)d\right]+1,\dots ,(2\frac{n}{d}-1)\frac{d}{2},\dots ,\frac{n}{d}d-1$. Hence, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $K_{\frac{n}{d}}$ and $\frac{d-2}{2}$ copies of $K_{\frac{n}{d},\frac{n}{d}}$. So by Theorem 2.1, $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\lceil \frac{(\frac{n}{d}-3)(\frac{n}{d}-4)}{12}\rceil +\frac{d-2}{2}\lceil \frac{{(\frac{n}{d}-2)}^2}{4}\rceil$. (ii) Let $d$ be an odd integer, then $S_H^C\left(I\right)$ has the following elements: $1,2,\dots ,\frac{d-1}{2},\frac{d+1}{2},\dots ,d-1$ $d+1,\dots ,\frac{3d-1}{2},\frac{3d+1}{2},\dots ,2d-1$ . . . $\left[(\frac{n}{d}-1)d\right]+1,\dots ,\frac{\left[(2\frac{n}{d}-1)d\right]-1}{2},\frac{\left[(2\frac{n}{d}-1)d\right]+1}{2},\dots ,\frac{n}{d}d-1$. Hence, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{d-1}{2}$ copies of $K_{\frac{n}{d},\frac{n}{d}}$ as in Fig. 1, where $1\le i\le \frac{d-1}{2}$. Then by Theorem 2.1, $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{d-1}{2}\lceil \frac{{(\frac{n}{d}-2)}^2}{4}\rceil$.

2.

Let $n$ be an odd integer; so, $2\in H$. Then by Theorem 2.4, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{d-1}{2}$ copies of $K_{\frac{n}{d},\frac{n}{d}}$ and by Theorem 2.1, $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{d-1}{2}\lceil \frac{{(\frac{n}{d}-2)}^2}{4}\rceil$.

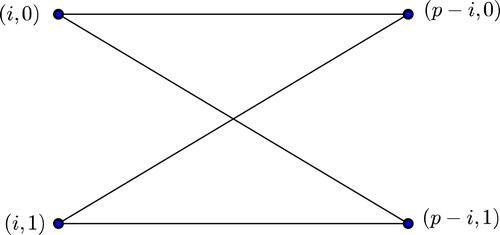
Fig. 1 The total graph of Theorem 3.11.

Example 3.12

Consider $R={\mathbb{Z}}_{18}$, $I=12{\mathbb{Z}}_{18}$ and $H=\left\{a\right|a\in {\mathbb{Z}}_{18},(a,18)=1\}$. Then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $K_3$ and two copies of $K_{3,3}$. Then $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\lceil \frac{(3-3)(3-4)}{12}\rceil +\frac{6-2}{2}\lceil \frac{{(3-2)}^2}{4}\rceil =2$.

Theorem 3.13

Let $R={\mathbb{Z}}_n\times {\mathbb{Z}}_n$, $I=0\times {\mathbb{Z}}_n$ and $H=\left\{(a,b)\right|a,b\in {\mathbb{Z}}_n\times {\mathbb{Z}}_n,(a,n)=1\}$. Then:

1.	If $n$ is an even integer, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $K_n$ and $\frac{n-2}{2}$ copies of $K_{n,n}$. In this case, $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\lceil \frac{(n-3)(n-4)}{12}\rceil +\frac{n-2}{2}\lceil \frac{{(n-2)}^2}{4}\rceil$.
2.	If $n$ is an odd integer, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{n-1}{2}$ copies of $K_{n,n}$. In this case $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{n-1}{2}\lceil \frac{{(n-2)}^2}{4}\rceil$.

Proof

1.

Let $n$ be an even integer. We claim that $I=S_H\left(I\right)$. By way of contradiction, if there is $(m,d)\in {\mathbb{Z}}_n\times {\mathbb{Z}}_n-(0\times {\mathbb{Z}}_n)$ such that $(t,l)(m,d)\in 0\times {\mathbb{Z}}_n$ for some $(t,l)\in H$, then $n|tm$, but $(t,n)=1$; so $n|m$, a contradiction. Hence $I=S_H\left(I\right)$. The number of elements of $({\mathbb{Z}}_n\times {\mathbb{Z}}_n)-S_H\left(I\right)$ is $n^2-n$. For every element $(a,b)\in S_H^C\left(I\right)$, we have $(a,b)+(-a,b)\in S_H\left(I\right)$. Let $(a,b)+(c,d)\in S_H\left(I\right)$ for $(a,b)$ and $(c,d)\in S_H^C\left(I\right)$. Then $a+c=0$ and this implies that $a=-c$. Hence, each element $(a,b)$ of $S_H^C\left(I\right)$ is just adjacent to $(-a,d)$ for every element $d\in {\mathbb{Z}}_n$. Because $n$ is even, so just for one element $0\ne a=\frac{n}{2}\in {\mathbb{Z}}_n$, $(a,b)\in S_H^C\left(I\right)$ is adjacent to $(a,c)$ for every $b,c\in {\mathbb{Z}}_n$. Hence, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $K_n$ and $\frac{n-2}{2}$ copies of $K_{n,n}$. Now by Theorem 2.1, $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\lceil \frac{(n-3)(n-4)}{12}\rceil +\frac{n-2}{2}\lceil \frac{{(n-2)}^2}{4}\rceil$.

2.

If $n$ is an odd integer, then $2\in H$. By Theorem 2.4, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{n-1}{2}$ copies of $K_{n,n}$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{n-1}{2}\lceil \frac{{(n-2)}^2}{4}\rceil$, by Theorem 2.1.

Example 3.14

Consider $R={\mathbb{Z}}_8\times {\mathbb{Z}}_8$, $I=0\times {\mathbb{Z}}_8$ and $H=\left\{(a,b)\right|(a,b)\in {\mathbb{Z}}_8\times {\mathbb{Z}}_8,(a,8)=1\}$. Then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $K_8$ and 3 copies of $K_{8,8}$. Hence $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=29$.

Theorem 3.15

Let $I=k{\mathbb{Z}}_n$, $H={\mathbb{Z}}_n-p{\mathbb{Z}}_n$ where $p$ is a prime number with $1<p\le n$, $\mid S_H\left(I\right)\mid =\alpha$ and $\mid {\mathbb{Z}}_n∕S_H\left(I\right)\mid =\beta$.

1.

If $p\ne 2$, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{\beta -1}{2}$ copies of $K_{\alpha ,\alpha }$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{\beta -1}{2}\lceil \frac{{(\alpha -2)}^2}{4}\rceil$.

2.

Let $p=2$. Then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $K_{\frac{n}{2^{l^{\prime }}}}$ and $\frac{2^{l^{\prime }}-2}{2}$ copies of $K_{\frac{n}{2^{l^{\prime }}},\frac{n}{2^{l^{\prime }}}}$. Hence $$g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\lceil \frac{(\frac{n}{2^{l^{\prime }}}-3)(\frac{n}{2^{l^{\prime }}}-4)}{12}\rceil +\frac{2^{l^{\prime }}-2}{2}\lceil \frac{{(\frac{n}{2^{l^{\prime }}}-2)}^2}{4}\rceil ,$$where $(k,n)=2^{l^{\prime }}{r}^{\prime }$ with $l^{\prime },r^{\prime }\in \mathbb{N}$ and $(2,r^{\prime })=1$.

Proof

By the proof of Theorem 3.11, $I=d{\mathbb{Z}}_n$, where $d=(k,n)$.

1.

If $p\ne 2$, then $2\in {\mathbb{Z}}_n-p{\mathbb{Z}}_n$. So, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{\beta -1}{2}$ copies of $K_{\alpha ,\alpha }$ by Theorem 2.4 and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{(\beta -1)}{2}\lceil \frac{{(\alpha -2)}^2}{4}\rceil$, by Theorem 2.1.

2.

Let $p=2$. If $n$ is odd, then $0\in H$ and this is impossible; so we assume that $n$ is even. It should be noted that $d$ is even; since if $d$ is odd, then $d\in H$ and $\varnothing \ne I\cap H$ that this implies that ${\mathbb{Z}}_n=S_H\left(I\right)$, which is not in our assumptions. Let $n=2^{l}r$ for $l,r\in \mathbb{N}$ where $(2,r)=1$. We can assume that $d=2^{l^{\prime }}{r}^{\prime }$ where $l^{\prime },r^{\prime }\in \mathbb{N}$ and $l^{\prime }\le l$, $r^{\prime }\le r$. Here, we claim that $S_H\left(I\right)=2^{l^{\prime }}{\mathbb{Z}}_n$. Suppose there is $m\in {\mathbb{Z}}_n-2^{l^{\prime }}{\mathbb{Z}}_n$ such that $d|tm$ for some $t\in H$, so $2^{l^{\prime }}|tm$. Hence $2^{l^{\prime }}|m$, a contradiction. Therefore, $S_H\left(I\right)\subseteq 2^{l^{\prime }}{\mathbb{Z}}_n$. Now, let $2^{l^{\prime }}{t}^{\prime }\in 2^{l^{\prime }}{\mathbb{Z}}_n$ for some $t^{\prime }\in {\mathbb{Z}}_n$. It is clear that $2^{l^{\prime }}{t}^{\prime }{r}^{\prime }\in I$, so $2^{l^{\prime }}{t}^{\prime }\in S_H\left(I\right)$. Hence, by an argument similar to the proof of Theorem 3.11, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $K_{\frac{n}{2^{l^{\prime }}}}$ and $\frac{2^{l^{\prime }}-2}{2}$ copies of $K_{\frac{n}{2^{l^{\prime }}},\frac{n}{2^{l^{\prime }}}}$. So $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\lceil \frac{(\frac{n}{2^{l^{\prime }}}-3)(\frac{n}{2^{l^{\prime }}}-4)}{12}\rceil +\frac{2^{l^{\prime }}-2}{2}\lceil \frac{{(\frac{n}{2^{l^{\prime }}}-2)}^2}{4}\rceil$ , by Theorem 2.1.

Example 3.16

Consider $R={\mathbb{Z}}_{64}$, $I=4{\mathbb{Z}}_{64}$ and $H={\mathbb{Z}}_{64}-2{\mathbb{Z}}_{64}$. Then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $K_{16,16}$ and $K_{16}$ such that $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=62$.

Theorem 3.17

Let $I=k{\mathbb{Z}}_n$, $H=\left\{a^s\right|s\ge 0\}$ such that $a|n$ with $(\frac{n}{a},a)=1$, $\mid S_H\left(I\right)\mid =\alpha$ and $\mid {\mathbb{Z}}_n∕S_H\left(I\right)\mid =\beta$.

1.

If there is at least one even number in $H$, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{\beta -1}{2}$ copies of $K_{\alpha ,\alpha }$. In this case $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{\beta -1}{2}\lceil \frac{{(\alpha -2)}^2}{4}\rceil$.

2.

Let there be no even number in $H$, $(d,\frac{n}{a})=l$ where $d=(k,n)$ and $n=rl$ for some $r\in \mathbb{N}$. ($1^{\prime }$). If $l$ is an even integer, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $K_r$ and $\frac{l-2}{2}$ copies of $K_{r,r}$. In this case $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\lceil \frac{(r-3)(r-4)}{12}\rceil +\frac{l-2}{2}\lceil \frac{{(r-2)}^2}{4}\rceil$. $\left(2^{\prime }\right)$. If $l$ is an odd integer, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{l-1}{2}$ copies of $K_{r,r}$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{l-1}{2}\lceil \frac{{(r-2)}^2}{4}\rceil$.

Proof

Note that by the proof of Theorem 3.11, $I=d{\mathbb{Z}}_n$.

1.

If there is at least one even element in $H$, then by Theorem 2.4, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{\beta -1}{2}$ copies of $K_{\alpha ,\alpha }$. Therefore, $g\left({\Gamma }_H^N\left(S_H^C\left(N\right)\right)\right)=\frac{(\beta -1)}{2}\lceil \frac{{(\alpha -2)}^2}{4}\rceil$, by Theorem 2.1.

2.

Let there be no even element in $H$. If $(d,\frac{n}{a})=1$, then $d|a$, since $n=\frac{n}{a}a$ where $(\frac{n}{a},a)=1$. Hence $\varnothing \ne I\cap H$ and this implies that ${\mathbb{Z}}_n=S_H\left(I\right)$, which is not the case. So, we assume that $(d,\frac{n}{a})=l\ne 1$. Put $I^{\prime }=l{\mathbb{Z}}_n$. We claim that $I^{\prime }=S_H\left(I\right)$. Suppose there is $m^{\prime }\in {\mathbb{Z}}_n-I^{\prime }$ such that $d|a^g{m}^{\prime }$, where $a^g\in H$ and $g\ge 0$, then $l|a^g{m}^{\prime }$. So, $l|m^{\prime }$, a contradiction. Conversely, we show that $d|al$ and this implies that $I^{\prime }\subseteq S_H\left(I\right)$. Let $d=n_{1}l$ and $\frac{n}{a}=n_{2}l$, for some $n_1,n_2\in \mathbb{N}$ (so $(n_1,n_2)=1$). We show that $n_1|a$; this implies that $n_{1}l|al$ and the proof is complete. Let $(n_1,a)=h$ (so $n_1=g_{1}h$ and $a=g_{2}h$, for some $g_1,g_2\in \mathbb{N}$ where $(g_1,g_2)=1$). By the fact that $d=n_{1}l$ and $d|n$, one has $g_{1}hl|g_{2}h{n}_{2}l$; so $g_1|g_2{n}_2$ and $(g_1,g_2)=1$ implies that $g_1|n_2$. This yields $g_1=1$ and so $n_1|a$. ($1^{\prime }$). Let $l$ be an even integer, then by the same way as the proof of Theorem 3.11, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $K_r$ and $\frac{l-2}{2}$ copies of $K_{r,r}$ . Hence, $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\lceil \frac{(r-3)(r-4)}{12}\rceil +\frac{l-2}{2}\lceil \frac{{(r-2)}^2}{4}\rceil$, by Theorem 2.1. $\left(2^{\prime }\right)$. Let $l$ be an odd integer. By the same way as the proof of Theorem 3.11, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{l-1}{2}$ copies of $K_{r,r}$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{l-1}{2}\lceil \frac{{(r-2)}^2}{4}\rceil$, by Theorem 2.1.

Example 3.18

Consider $R={\mathbb{Z}}_{60}$, $I=15{\mathbb{Z}}_{60}$ and $H=\left\{3^s\right|s\ge 0\}$. Then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $2$ copies of $K_{12,12}$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=50$.

Theorem 3.19

Let $I=k{\mathbb{Z}}_n$, $H=\{1,t\}$ with $n|t^2-1$, $\mid S_H\left(I\right)\mid =\alpha$ and $\mid {\mathbb{Z}}_n∕S_H\left(I\right)\mid =\beta$.

1.

If $t$ is an even integer, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{\beta -1}{2}$ copies of $K_{\alpha ,\alpha }$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{\beta -1}{2}\lceil \frac{{(\alpha -2)}^2}{4}\rceil$.

2.

let $t$ be an odd integer and $(k,n)=d$. $\left(1^{\prime }\right)$. If $d$ is an even integer, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $K_{\frac{n}{d}}$ and $\frac{d-2}{2}$ copies of $K_{\frac{n}{d},\frac{n}{d}}$. In this case $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\lceil \frac{(\frac{n}{d}-3)(\frac{n}{d}-4)}{12}\rceil +\frac{d-2}{2}\lceil \frac{{(\frac{n}{d}-2)}^2}{4}\rceil$. ($2^{\prime }$). If $d$ is an odd integer, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{d-1}{2}$ copies of $K_{\frac{n}{d},\frac{n}{d}}$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{d-1}{2}\lceil \frac{{(\frac{n}{d}-2)}^2}{4}\rceil$.

Proof

1.

Let $t$ be an even integer. In view of Theorem 2.4, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{\beta -1}{2}$ copies of $K_{\alpha ,\alpha }$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{\beta -1}{2}\lceil \frac{{(\alpha -2)}^2}{4}\rceil$.

2.

By the proof of Theorem 3.11, $I=d{\mathbb{Z}}_n$. Let $t$ be an odd integer. We claim that $I=S_H\left(I\right)$. Otherwise, there is $a\in {\mathbb{Z}}_n-I$ such that $d|at$. So $d|a{t}^2$. By the assumption $d|t^2-1$, hence $d|a$ and this implies that $a\in I$ , a contradiction. Thus, $I=S_H\left(I\right)$. ($1^{\prime }$) If $d$ is an even integer, then we proceed in the proof of Theorem 3.11. So ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $K_{\frac{n}{d}}$ and $\frac{d-2}{2}$ copies of $K_{\frac{n}{d},\frac{n}{d}}$. Then $$g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\lceil \frac{(\frac{n}{d}-3)(\frac{n}{d}-4)}{12}\rceil +\frac{d-2}{2}\lceil \frac{{(\frac{n}{d}-2)}^2}{4}\rceil ,$$by Theorem 2.1. ($2^{\prime }$) If $d$ is an odd integer, then we proceed in the proof of Theorem 3.11. Hence, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{d-1}{2}$ copies of $K_{\frac{n}{d},\frac{n}{d}}$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{d-1}{2}\lceil \frac{{(\frac{n}{d}-2)}^2}{4}\rceil$, by Theorem 2.1.

Example 3.20

Consider $R={\mathbb{Z}}_{50}$, $I=5{\mathbb{Z}}_{50}$ and $H=\{1,49\}$. Then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of two copies of $K_{10,10}$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=32$.

Theorem 3.21

Let $R={\mathbb{Z}}_n\times {\mathbb{Z}}_n$, $I=0\times {\mathbb{Z}}_n$, $H=\{(1,1),(t,t)\}$ with $n|t^2-1$, $\mid S_H\left(I\right)\mid =\alpha$ and $\mid {\mathbb{Z}}_n∕S_H\left(I\right)\mid =\beta$.

1.

If $t$ is an even integer, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{\beta -1}{2}$ copies of $K_{\alpha ,\alpha }$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{\beta -1}{2}\lceil \frac{{(\alpha -2)}^2}{4}\rceil$.

2.

Let $t$ be an odd integer. (i) If $n$ is an even integer, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $K_n$ and $\frac{n-2}{2}$ copies of $K_{n,n}$. In this case, $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\lceil \frac{(n-3)(n-4)}{12}\rceil +\frac{n-2}{2}\lceil \frac{{(n-2)}^2}{4}\rceil$. (ii) If $n$ is an odd integer, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{n-1}{2}$ copies of $K_{n,n}$. In this case $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{n-1}{2}\lceil \frac{{(n-2)}^2}{4}\rceil$.

Proof

1.

If $t$ is an even integer, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{\beta -1}{2}$ copies of $K_{\alpha ,\alpha }$ by Theorem 2.4 and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{\beta -1}{2}\lceil \frac{{(\alpha -2)}^2}{4}\rceil$.

2.

Let $t$ be an odd integer. We claim that $I=S_H\left(I\right)$. Otherwise, there is $(a,b)\in {\mathbb{Z}}_n\times {\mathbb{Z}}_n$ such that $(a,b)(t,t)\in I$ where $a\ne 0$ and $b$ is an arbitrary element of ${\mathbb{Z}}_n$. So $n|at$; then $n|a{t}^2$. By the assumption $n|t^2-1$, so $n|a$ and this implies that $a=0$, a contradiction. Hence $I=S_H\left(I\right)$. The remaining is similar to proof of Theorem 3.13.

Example 3.22

Consider $R={\mathbb{Z}}_{21}\times {\mathbb{Z}}_{21}$, $I=0\times {\mathbb{Z}}_{21}$ and $H=\{(1,1),(13,13)\}$. Then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $10$ copies of $K_{21,21}$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=910$.

Theorem 3.23

Let ${\mathbb{Z}}_p$ denote the field of $p$ elements where $p>2$ is a prime number, $R={\mathbb{Z}}_p\times {\mathbb{Z}}_{2^m}$ where $m\in \mathbb{N}$ and $I=0\times {\mathbb{Z}}_{2^m}$. Let $H$ be one of the following sets: $\left\{(1,1)\right\},\{(1,1),(2,1)\},\dots ,\{(1,1),(2,1),\dots ,(p-1,1)\},\left\{(1,0)\right\},\{(1,0),(2,0)\}$, …, $\{(1,0),(2,0),\dots ,(p-1,0)\}$.

1.	If $m=1$, then ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is planar.
2.	If $m>1$, then $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{p-1}{2}\lceil \frac{{(2^m-2)}^2}{4}\rceil$.

Proof

We note that $I=S_H\left(I\right)$ for every positive integer $m$ and all cases of $H$. Otherwise, there exists $(a,c)\in {\mathbb{Z}}_p\times {\mathbb{Z}}_{2^m}$ such that $a\ne 0$ and $p|at$ for some $(t,b)\in H$, where $b\in {\mathbb{Z}}_2$. Because $(p,t)=1$, so $p|a$, a contradiction. Hence, in all cases, $I=S_H\left(I\right)$.

1.

If $m=1$, for every $(a,b)\in S_H^C\left(I\right)$, we have $(a,b)+(-a,b)\in S_H\left(I\right)$, where $a\in Z_p$ and $b\in Z_2$. So, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{p-1}{2}$ copies of $K_{2,2}$, where $R={\mathbb{Z}}_p\times {\mathbb{Z}}_2$ and $I=0\times {\mathbb{Z}}_2$, as Fig. 2, where $1\le i\le \frac{p-1}{2}$. Hence $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=0$ , by Theorem 2.1.

2.

In the same way of the case 1, for $R={\mathbb{Z}}_p\times {\mathbb{Z}}_{2^m}$ with $m\in \mathbb{N}$ and $m>1$, ${\Gamma }_H^I\left(S_H^C\left(I\right)\right)$ is a disjoint union of $\frac{p-1}{2}$ copies of $K_{2^m,2^m}$ and $g\left({\Gamma }_H^I\left(S_H^C\left(I\right)\right)\right)=\frac{p-1}{2}\lceil \frac{{(2^m-2)}^2}{4}\rceil$, where $I=0\times {\mathbb{Z}}_{2^m}$.

Fig. 2 The total graph of Theorem 3.23 (1).