Binomial trees are graceful

Abstract

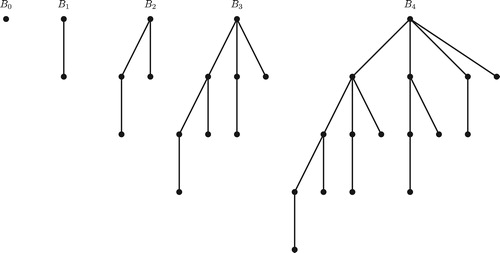
The binomial tree $B_0$ consists of a single vertex. The binomial tree $B_k$ is an ordered tree defined recursively. The binomial tree $B_k$ consists of two binomial trees $B_{k-1}$ that are linked together: the root of one is the leftmost child of the root of the other. The popular Graceful Tree Conjecture states that every tree is graceful. In this paper, we show that binomial trees $B_k$ is graceful for every $k\ge 0$.

Keywords:

• Graceful Tree
• Graceful Tree Conjecture
• Binomial tree

1 Introduction

All the graphs considered in this paper are finite simple graphs. Terms that are not defined here can be referred from the book [1]. In 1963, at the Smolenice symposium in 1963, Ringel [2] conjectured that $K_{2n+1}$, the complete graph on $2n+1$ vertices, can be decomposed into $2n+1$ isomorphic copies of a given tree with $n$ edges. In 1965, Kotzig [3] also conjectured that the complete graph $K_{2n+1}$ can be cyclically decomposed into $2n+1$ copies of a given tree with $n$ edges. In an attempt to settle these two conjectures, in 1967, in his classical paper [4] Rosa introduced a hierarchical series of ‘valuations’ of a graph called $\rho ,\sigma ,\beta ,\alpha$ and used these valuations to investigate the cyclic decomposition of complete graphs. Later, $\beta$-valuation was called graceful by Golomb [5], and this term is being widely used. A function $f$ is called a graceful labeling of a graph $G$ with $m$ edges, if $f$ is an injective function from $V\left(G\right)$ to $\{0,1,2,\dots ,m\}$ such that, when every edge $uv$ is assigned the edge label $|f\left(u\right)-f\left(v\right)|$, then the resulting edge labels are distinct. A graph which admits graceful labeling is called a graceful graph. In the same paper [4] Rosa proved the following significant theorem.

Theorem 1

Rosa [4] If a graph $T$ with $n$ edges has a graceful labeling, then $K_{2n+1}$ can be cyclically decomposed into $2n+1$ copies of $T$.

This result led to the Rosa–Kotzig–Ringel Conjecture popularly called Graceful Tree Conjecture, which states that “All trees are graceful”. The graceful tree conjecture has been the focus of many papers for over four decades. So far, no proof of the truth or falsity of the conjecture has been found. In the absence of a generic proof, one approach used in investigating the Graceful Tree Conjecture is proving the gracefulness of specialized classes of trees. Aldred and Mckay [6] used computer search to prove that all trees on at most 27 vertices are graceful. Michael Horton [7] has verified that all trees with at most 29 vertices are graceful. Fang [8] has verified that all trees with at most 35 vertices are graceful. Rosa [4] has proved that all paths and caterpillars are graceful. Some special classes of lobsters were shown to be graceful by Ng [9] and Wang et al. [10]. Chen, Lu and Yeh [11] have shown that all firecrackers are graceful. Sethuraman and Jeba Jesintha [12] have shown that all banana trees are graceful. Pastel and Raynaud [13] have shown that olive trees are graceful. Bermond and Sotteau [14] have proved that all symmetrical trees are graceful. One of the general results proved on Graceful Tree Conjecture is the result due to Havier et al. [15] that all trees of diameter five are graceful. Using Havier’s branch moving technique, Balbuena et al. [16] have shown that trees having an even or quasi even degree sequence are graceful. Koh, Rogers and Tan [17] gave different methods to construct a bigger graceful tree from smaller graceful trees. Burzio and Ferrarese [18] extended the method of Koh et al. and consequently they have shown that the subdivision of every graceful tree is graceful. Cahit [19] has exhibited canonic labeling technique for proving the gracefulness of a class of rooted trees. Sethuraman and Venkatesh [20] have given a method of attaching caterpillars recursively with other caterpillars to generate graceful trees. For an exhaustive survey on Graceful Tree Conjecture, refer the excellent survey by Gallian [21], for other related results refer [22,23].

The binomial tree $B_0$ consists of a single vertex. The binomial tree $B_k$ is an ordered tree defined recursively. The binomial tree $B_k$ consists of two binomial trees $B_{k-1}$ that are linked together: the root of one is the leftmost child of the root of the other. Note that there are $2^k$ vertices in the binomial tree $B_k$. Fig. 1 shows the binomial trees $B_0$ through $B_4$.

Fig. 1 Binomial Trees of order 0, 1, 2, 3 and 4.

For more details about binomial trees refer [24]. In this paper, we show that all binomial trees are graceful.

2 Main result

In this section, we prove that the binomial tree $B_k$ is graceful, for all $k\ge 0$. In fact, we show that the binomial trees $B_k$ admits $\alpha$-labeling, a stronger version of graceful labeling. A graceful labeling $f$ of a graph $G$ with $q$ edges is said to be an $\alpha$-valuation if there exists a $\lambda$ such that $f\left(u\right)\le \lambda <f\left(v\right)$ or $f\left(v\right)\le \lambda <f\left(u\right)$ for every edge $uv\in E\left(G\right)$, where $\lambda$ is called the width of the $\alpha$-valuation.

Theorem 2

The binomial tree $B_k$, for all $k\ge 0$ is graceful.

Proof

We prove that binomial tree of order $k$, $B_k$, for all $k\ge 0$ admits a stronger version of the graceful labeling, the $\alpha$-labeling. More precisely, we prove that the binomial tree $B_k$ admits $\alpha$-labeling with width $\lambda =2^{k-1}-1$, for $k\ge 1$. It is obvious that $B_0$, a single vertex tree admits $\alpha$-labeling. We prove this result by induction on $k$, the order of the binomial tree $B_k$. 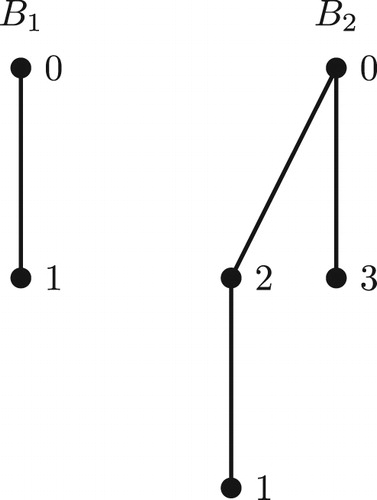When $k=\text{1,2}$, the $\alpha$-labelings of $B_1$ and $B_2$ respectively having the width $\lambda =0$, and $\lambda =1$ are given in Fig. 2.

By induction, we assume that the binomial tree $B_{k-1}$ admits $\alpha$-labeling with $\lambda =2^{k-2}-1$, where $k\ge 2$. By the definition of $\alpha$-labeling, the vertices of $B_{k-1}$ are labeled with $0,1,2,\dots ,2^{k-1}-1$. Under this $\alpha$-labeling, the sequence of labels $(0,1,2,\dots ,2^{k-2}-1)$ and the sequence of labels $(2^{k-2},2^{k-2}+1,\dots ,2^{k-1}-1)$ are respectively referred to as the first half sequence and the second half sequence of the labels of vertices of $B_{k-1}$.

Consider the binomial tree $B_k$ of order $k$, $k\ge 2$. For the convenience, we denote $B_0$, a single vertex tree and we denote $B_k=\left(B_{k-1}^{\left(1\right)}\cup B_{k-1}^{\left(2\right)}\right)+e$ for $k\ge 1$, where $B_{k-1}^{\left(1\right)}$ and $B_{k-1}^{\left(2\right)}$ are the two copies of $B_{k-1}$ and $e$ is the new edge added between the roots of $B_{k-1}^{\left(1\right)}$ and $B_{k-1}^{\left(2\right)}$ (The $B_{k-1}^{\left(1\right)}$ is referred to as the first copy of $B_{k-1}$ and $B_{k-1}^{\left(2\right)}$ is referred to as the second copy of $B_{k-1}$). As $B_{k-1}$ has an $\alpha$-labeling, the two copies of $B_{k-1}$, $B_{k-1}^{\left(1\right)}$ and $B_{k-1}^{\left(2\right)}$ also have the same $\alpha$-labeling. Consider the $B_{k-1}^{\left(1\right)}$ and $B_{k-1}^{\left(2\right)}$ as $\alpha$-labeled tree with their $\alpha$-labeling. Consequently, tree $B_k$ is also a labeled tree labeled from the set $\{0,1,2,\dots ,2^{k-1}-1\}$ such that every label is assigned exactly to two vertices of $B_k$ of which one vertex is in $B_{k-1}^{\left(1\right)}$ and the other vertex is in $B_{k-1}^{\left(2\right)}$. Hereafter, we refer the vertices of $B_{k-1}^{\left(i\right)}$, for $i=\text{1,2}$ in $B_k$ with their vertex labels that are defined by the $\alpha$-labeling of $B_{k-1}^{\left(i\right)}$, for $i=\text{1,2}$.

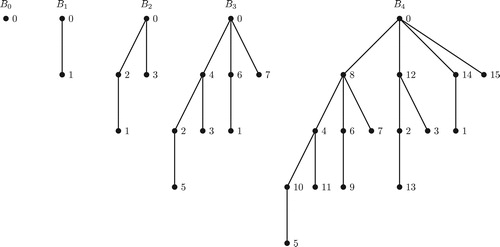
Consider the first half sequence of vertex labels of $B_{k-1}^{\left(1\right)}$ and the second half sequence of vertex labels of $B_{k-1}^{\left(2\right)}$ and add $2^{k-1}$ to each label in both of the sequences and retain the original labels for the remaining vertices of $B_{k-1}^{\left(i\right)}$, for $i=\text{1,2}$. Thus we have the labels of the vertices of $B_{k-1}^{\left(i\right)}$, for $i=\text{1,2}$ after the above relabeling as given in Table 1.

From Table 1, the labels of the vertices of $B_{k-1}^{\left(i\right)}$, for $i=\text{1,2}$ can be arranged as the sequence of labels from $S_1^{\left(2\right)}$, followed by the sequence of labels from $S_2^{\left(1\right)}$, followed by the sequence of labels from $S_1^{\left(1\right)}$ and followed by the sequence of labels from $S_2^{\left(2\right)}$ as a monotonic sequence of vertex labels $0,1,2,\dots ,2^{k-2}-1,2^{k-2},2^{k-2}+1,\dots ,2^{k-1}-1,2^{k-1},\dots ,2^k-1$. Hence the labels of the vertices of $B_k$ are distinct.

Since $\lambda$ of $B_{k-1}^{\left(i\right)}$, for $i=\text{1,2}$ is $2^{k-2}-1$, for any edge in $B_{k-1}^{\left(i\right)}$, the label of the one end vertex of the edge is in the first half sequence of vertex labels and the label of the other end vertex of the edge is in the second half sequence of vertex labels corresponding to its $\alpha$-labeling.

Let $x$ be the edge label of an edge $e=uv$ in $B_{k-1}^{\left(1\right)}$ with vertex labels $l\left(u\right)$, $l\left(v\right)$ in $B_{k-1}^{\left(1\right)}$. If $l\left(u\right)<l\left(v\right)$, then $l\left(u\right)\in \{0,1,2,\dots ,2^{k-2}-1\}$ and $l\left(v\right)\in \{2^{k-2},2^{k-2}+1,\dots ,2^{k-1}-1\}$. Therefore, by the above relabeling procedure in $B_k$, $u$ gets the label $l\left(u\right)+2^{k-1}$ and the label of $v$ is retained. Thus, the edge $e=uv$ of $B_{k-1}^{\left(1\right)}$ gets the label $|l\left(u\right)+2^{k-1}-l\left(v\right)|=|-\{l\left(u\right)+2^{k-1}-l\left(v\right)\}|=|-(2^{k-1}-\{l\left(v\right)-l\left(u\right)\})|=|-(2^{k-1}-x)|=2^{k-1}-x$ in $B_k$. Similarly, if $l\left(v\right)<l\left(u\right)$, then the edge $e=uv$ of $B_{k-1}^{\left(1\right)}$ gets the label $2^{k-1}-x$ in $B_k$.

Let $x$ be the edge label of an edge $e=uv$ in $B_{k-1}^{\left(2\right)}$ with vertex labels $l\left(u\right),l\left(v\right)$ in $B_{k-1}^{\left(2\right)}$ corresponding to its $\alpha$-labeling. If $l\left(u\right)<l\left(v\right)$, then $l\left(u\right)\in \{0,1,2,\dots ,2^{k-2}-1\}$ and $l\left(v\right)\in \{2^{k-2},2^{k-2}+1,\dots ,2^{k-1}-1\}$. Therefore by the above relabeling procedure, $v$ gets the label $l\left(v\right)+2^{k-1}$ and the label of $u$ is retained. Thus, the edge $e=uv$ of $B_{k-1}^{\left(2\right)}$ gets the label $|l\left(v\right)+2^{k-1}-l\left(v\right)|=|2^{k-1}+l\left(v\right)-l\left(u\right)|=|2^{k-1}+x|=2^{k-1}+x$ in $B_k$. Similarly if $l\left(v\right)<l\left(u\right)$, then the edge $e=uv$ gets the relabel $2^{k-1}+x$ in $B_k$. Thus, after the relabeling, the $2^{k-1}-1$ edges in $B_{k-1}^{\left(1\right)}$ will get the edge labels as $2^{k-1}-1,2^{k-1}-2,\dots ,2^{k-1}-(2^{k-1}-1)=1$ in $B_k$. Therefore, after the relabeling, the $2^{k-1}-1$ edges in $B_{k-1}^{\left(2\right)}$ will get the edge labels as $2^{k-1}+1,2^{k-1}+2,\dots ,2^{k-1}+2^{k-1}-1=2^k-1$ in $B_k$. Also note that after the relabeling process, the label of the root of $B_{k-1}^{\left(1\right)}$ relabeled as $2^{k-1}$ and the label of the root of $B_{k-1}^{\left(2\right)}$ is retained as $0$ in $B_{k-1}^{\left(2\right)}$. Therefore the edge connecting the roots of $B_{k-1}^{\left(1\right)}$ and $B_{k-1}^{\left(2\right)}$ gets the edge label $2^{k-1}$ in $B_k$. Hence the edges of $B_k$ get the distinct edge labels $1,2,3,\dots ,2^k-1$. Hence the relabeling procedure indeed gives $\alpha$-labeling for $B_k$ having the width $2^{k-1}-1$. This completes the induction.

Table 1 The First and Second half Sequences of $B_{k-1}^{\left(i\right)}$, for $i=1,2$ after the relabeling.

$S_1^{\left(1\right)}:2^{k-1},2^{k-1}+1,\dots ,2^{k-1}+2^{k-2}-1$	$S_1^{\left(2\right)}:0,1,2,\dots ,2^{k-2}-2,2^{k-2}-1$
First half sequence of $B_{k-1}^{\left(1\right)}$	First half sequence of $B_{k-1}^{\left(2\right)}$
$S_2^{\left(1\right)}:2^{k-2},2^{k-2}+1,\dots ,2^{k-1}-1$	$S_2^{\left(2\right)}:2^{k-1}+2^{k-2},\dots ,2^k-2,2^k-1$
Second half sequence of $B_{k-1}^{\left(1\right)}$	Second half sequence of $B_{k-1}^{\left(2\right)}$

Fig. 2 Gracefully labeled Binomial Trees $B_1$ and $B_2$.

The following two significant theorems indicate that the $\alpha$-labeled graphs decomposes the complete graphs and complete bipartite graphs.

Theorem 3

Rosa [4] If a graph $G$ with $q$ edges has an $\alpha$-valuation, then there exists a cyclic decomposition of the complete graph $K_{2cq+1}$ into subgraphs isomorphic to $G$, where $c$ is an arbitrary natural number.

Theorem 4

El-zanati and Vanden Eynden [25] If $G$ has $q$ edges and admits an $\alpha$-valuation, then $K_{mq,nq}$ can be decomposed into subgraphs isomorphic to $G$ for all positive integers $m$ and $n$.

Since the binomial tree $B_k$, $k\ge 0$ admits $\alpha$-labeling, the following corollary is a direct consequence of Theorems 3 and 4.

Corollary 4.1

The complete graph $K_{2cq+1}$ and the complete bipartite graph $K_{mq,nq}$ can be decomposed into isomorphic copies of the binomial tree $B_k$ for every $k\ge 0$, where $m,n,c\in {\mathit{Z}}^{+}$.

Illustration

Gracefully labeled binomial trees $B_0,B_1,B_3,B_4$ and $B_5$ are given in Figs. 3 and 4.

Fig. 3 Gracefully labeled Binomial Trees of order 0, 1, 2, 3 and 4.

Fig. 4 Gracefully labeled Binomial Tree of order 5.