Face counting formula for toric arrangements defined by root systems

Peer review under responsibility of Kalasalingam University.

Abstract

A toric arrangement is a finite collection of codimension-1 subtori in a torus. The intersections of these subtori stratify the ambient torus into faces of various dimensions. The incidence relations among these faces give rise to many interesting combinatorial problems. One such problem is to obtain a closed-form formula for the number of faces in terms of the intrinsic arrangement data. In this paper we focus on toric arrangements defined by crystallographic root systems. Such an arrangement is equipped with an action of the associated Weyl group. The main result is a formula that expresses the face numbers in terms of a sum of indices of certain subgroups of this Weyl group.

Keywords:

• Toric arrangements
• Face enumerations
• $f$-vector
• Affine Weyl groups

1 Introduction

An arrangement of hyperplanes is a locally finite collection of hyperplanes in a vector space. Such a collection defines a stratification of the vector space into relatively open convex subsets. The incidence relations among these strata give rise to interesting problems in combinatorics; many of them still unsolved. The simplest possible example of a hyperplane arrangement is an arrangement of lines in the Euclidean plane. Such a collection determines a stratification of the plane consisting of vertices (intersections of lines), edges (maximal connected components of the lines not containing any vertex) and chambers (maximal connected components of the plane containing neither the edges nor the vertices). The combinatorics that emerges from these intersections is intriguing. This is evident by the number of interesting problems and conjectures described in Grünbaum’s exposition [1]. A classical source for systematic discussion of combinatorial aspects of hyperplane arrangements is [2, Chapter 18]. For a more modern exposition we refer the reader to Richard Stanley’s notes [3].

Let $\mathcal{A}$ be an arrangement of hyperplanes in ${\mathbb{R}}^l$. The rank of $\mathcal{A}$ is the dimension of the largest subspace spanned by the normals to hyperplanes in $\mathcal{A}$. An arrangement is essential if it is of rank $l$. We call $\mathcal{A}$ a central arrangement if all the hyperplanes pass through a common point; otherwise we call $\mathcal{A}$ a non-central arrangement.

There are two posets associated with $\mathcal{A}$, namely, the face poset and the intersection poset. They encode the combinatorial information about the arrangement.

Definition 1

The intersection poset $L\left(\mathcal{A}\right)$ of a hyperplane arrangement $\mathcal{A}$ is defined as the set of all nonempty intersections of hyperplanes, including ${\mathbb{R}}^l$ itself as the empty intersection, ordered by reverse inclusion.

The rank of each element is the codimension of the corresponding intersection. In general $L\left(\mathcal{A}\right)$ is a (meet) semilattice; it is a lattice if and only if the arrangement is central.

Definition 2

The characteristic polynomial of an arrangement $\mathcal{A}$ is: $p(\mathcal{A},t)≔\sum _{X\in L\left(\mathcal{A}\right)}\mu ({\mathbb{R}}^l,X)\cdot t^{dim\left(X\right)},$where $\mu (,)$ denotes the Möbius function of $L\left(\mathcal{A}\right)$ (see Definition 12).

The hyperplanes of $\mathcal{A}$ induce a stratification of ${\mathbb{R}}^l$; the components of each stratum are (relatively) open polyhedra called faces of $\mathcal{A}$.

Definition 3

The face poset $\mathcal{F(A)}$ of $\mathcal{A}$ is the set of all faces ordered by topological inclusion: $F\le G$ if and only if $F\subseteq \overline{G}$.

The set of all top-dimensional faces (also called chambers) is denoted by $\mathcal{C}\left(\mathcal{A}\right)$. A natural question regarding chambers asks how does the cardinality $\mathcal{C}\left(\mathcal{A}\right)$ depends on the intersection data? Zaslavsky in his fundamental treatise [4] studied the relationship between the intersection lattice of an arrangement and the number of chambers. His main result is as follows:

Theorem 4

Theorem A [4]

Let $\mathcal{A}$ be a hyperplane arrangement in ${\mathbb{R}}^l$ with $L\left(\mathcal{A}\right)$ as its intersection poset and let $p(\mathcal{A},t)$ be the associated characteristic polynomial. Then $\mathcal{C}\left(\mathcal{A}\right)=\sum _{X\in L\left(\mathcal{A}\right)}\mu ({\mathbb{R}}^l,X)={(-1)}^{l}p(\mathcal{A},-1).$

Given a hyperplane arrangement $\mathcal{A}$ denote by $f_i$ the number of $i$-dimensional faces (for example, $f_l$ is the number of chambers). One of the combinatorial problems in the theory of hyperplane arrangements is to obtain a complete characterization of these numbers. These numbers satisfy the Euler relation $\sum _{i=0}^l{(-1)}^i{f}_i={(-1)}^l.$One would like to find more such relations satisfied by $f_i$’s. Another aspect of this problem is to construct a combinatorially defined set whose elements are in one-to-one correspondence with, say, $i$-dimensional faces of the arrangement. It should be noted that such a problem can only be solved by looking at ‘nice’ families of hyperplane arrangement. We refer the reader to [3] for more details.

Partitioning problems for spaces other than Euclidean and projective spaces have not been extensively studied. To our knowledge the first paper that deals with a more general situation is by Zaslavsky [5]. He derives a formula for counting the number of connected components of a topological space when dissected by finitely many of its subspaces. He showed that not only the combinatorics of the intersections (as encoded by the Möbius function) but also their geometry (as captured by the Euler characteristic) plays a role. In recent years several authors have considered toric arrangements. A toric arrangement is a finite collection of codimension-$1$ subtori in a torus. The formula for the number of chambers for such arrangements was first discovered by Ehrenborg et al. in [6]; it also appears in [7] and [8]. Recently, Shnurnikov has characterized the set of all possible values of top-dimensional faces for arrangements in a $2$-torus in [9] and for arrangements in higher-dimensional tori in [10]. See also [11] for a complete characterization of face numbers in case of arrangements in a $2$-torus.

The aim of this paper is to derive a closed form formula for the number of faces of toric arrangements defined by crystallographic root systems. The paper is organized as follows. In Section 2 we introduce toric arrangements in full generality and fix notations. In Section 3 we start with a brief exposition on reflection groups, root systems and associated reflection arrangements. Then we move on to introduce toric Weyl arrangements using affine Weyl groups and prove the face counting formula. We also show that these face numbers satisfy Dehn–Sommerville relations.

2 Toric arrangements

The $l$-dimensional torus ${\mathbb{T}}^l$ is the quotient space ${\mathbb{R}}^l∕{\mathbb{Z}}^l$. When identified with the set ${[0,1)}^l$ it forms an abelian group with the group structure given by the componentwise addition modulo $1$. There is also a ‘multiplicative’ way of looking at the torus when we consider it as the product ${\left(S^1\right)}^l$. The group structure here is the componentwise multiplication of complex numbers of modulus $1$. However, throughout this paper, we stick to the additive way. In this section we define toric arrangements and collect some relevant background material.

We assume the reader’s familiarity with basic algebraic topology and combinatorics. The combinatorics of posets and lattices that we need can be found in Stanley’s book [12].

The field of toric arrangements is fairly recent. Ehrenborg, Readdy and Slone mainly study the problem of enumerating faces of the induced decomposition of the torus in [6]. On the other hand a number theoretic aspect is explored by Lawrence in [7].

We denote by $\pi :{\mathbb{R}}^l\to {\mathbb{T}}^l$ the quotient map. Note that $\pi$ is also the covering map and ${\mathbb{R}}^l$ is the universal cover. We say that a $k$-subspace $V$ of ${\mathbb{R}}^l$ is rational if it is the kernel of an $n\times l$ matrix $A$ with integer entries. The image $\overline{V}≔\pi \left(V\right)$ is a closed subgroup of ${\mathbb{T}}^l$. Topologically $\overline{V}$ is disconnected and each connected component is a $k$-torus. The connected components are known as toric subspaces (or cosets) of $\overline{V}$. Let ${}_0\overline{V}$ denote the coset containing $\mathbf{0}$. Then $\overline{V}{∕}_0\overline{V}$ is a finite abelian group whose order is the number of cosets of $\overline{V}$. One can check that every closed subgroup of the torus arises in this manner. It is important to note that the subgroup $\overline{V}$ depends only on the free abelian group generated by the row-space of $A$. Hence one can assume that the rows of $A$ form a basis for the row-space. The subgroup $\overline{V}$ is connected if and only if the greatest common divisor of all the $k\times k$ minors of $A$ is $1$.

A toric hyperplane is a toric subspace of codimension-$1$, i.e., it is the projection of an affine hyperplane in ${\mathbb{R}}^l$. We have the following definition.

Definition 5

A toric arrangement in ${\mathbb{T}}^l$ is a finite collection $\mathcal{A}=H_1,\dots ,H_n$ of toric hyperplanes.

To every toric arrangement there is an associated periodic hyperplane arrangement $\tilde{\mathcal{A}}$ in ${\mathbb{R}}^l$. The inverse image of each $H_i$ under the covering map $\pi$ is the union of parallel integer translates of a codimension-$1$ subspace. We say that a toric arrangement is essential if the associated hyperplane arrangement $\tilde{\mathcal{A}}$ is essential. Without loss of generality we assume that a toric arrangement is always essential; which forces $n\ge l$. If this is not the case then the enumerative problems that we consider in this paper reduce to equivalent problems in a torus of smaller dimension.

The hyperplane arrangement $\tilde{\mathcal{A}}$ induces a stratification of ${\mathbb{R}}^l$ such that these open strata are relative interiors of convex polytopes. A nonempty subset $F\subset {\mathbb{T}}^l$ is said to be a face of the toric arrangement $\mathcal{A}$ if there is a stratum $\tilde{F}$ of $\tilde{\mathcal{A}}$ such that $\pi \left(\tilde{F}\right)=F$. The dimension of $F$ is the dimension of the support of $\tilde{F}$ and it is denoted by $dim\left(F\right)$.

It is important to note that the closure of $F$ in ${\mathbb{T}}^l$ need not be homeomorphic to a disk. While a toric arrangement stratifies the ambient torus, this stratification need not define a regular cell structure but it does have special properties.

Definition 6

A polytopal complex is a cell complex $(X,{e_{\lambda }}_{\lambda \in \Lambda })$ with the following additional data.

(1)

Every cell $e_{\lambda }$ is equipped with a $k$-polytopal cell structure which is a pair $(P_{\lambda },{\varphi }_{\lambda })$ of a $k$-convex polytope and a cellular map ${\varphi }_{\lambda }:P_{\lambda }\to X$ such that ${\varphi }_{\lambda }\left(P_{\lambda }\right)=\overline{e_{\lambda }}$ and the restriction of ${\varphi }_{\lambda }$ to the interior of $P_{\lambda }$ is a homeomorphism.

(2)	If $e_{\mu }\cap \overline{e_{\lambda }}\ne \varnothing$ then $e_{\mu }\subset \overline{e_{\lambda }}$.

(3)	For every face $P^{\prime }$ of $P_{\lambda }$, there exists a cell $e_{\mu }$ in $X$ and a map $b:Q_{\mu }\to \partial P_{\lambda }$ such that $b\left(\mathrm{Int}{Q}_{\mu }\right)=P^{\prime }$ and ${\varphi }_{\lambda }\circ b={\varphi }_{\mu }$.

Example 7

Recall that a $\Delta$-complex is a quotient space of a collection of disjoint simplices obtained by identifying certain of their faces via canonical linear homeomorphisms that preserve the ordering of vertices. This is an example of a polytopal complex where all the indexing polytopes are required to be simplices.

The following lemma is a straightforward application of the fact that the covering map $\pi$ is stratification preserving.

Lemma 8

If $\mathcal{A}$ is a toric arrangement in ${\mathbb{T}}^l$ then the induced stratification is polytopal.

Definition 9

The intersection poset $L\left(\mathcal{A}\right)$ of a toric arrangement $\mathcal{A}$ is defined to be the set of all connected components arising from all possible intersections of the toric hyperplanes ordered by reverse inclusion.

By convention, the ambient torus corresponds to the empty intersection. The intersection poset is graded by the codimensions of the intersections. Before proceeding further let us look at a couple of examples.

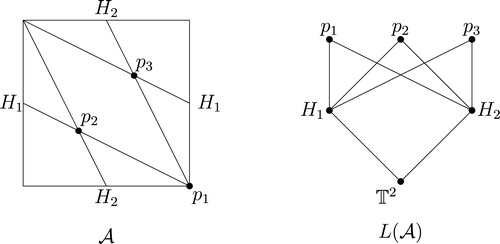
Example 10

Let $\mathcal{A}$ be the toric arrangement in ${\mathbb{T}}^2$ obtained by projecting the lines $x=-2y$ and $y=-2x$. These toric hyperplanes intersect in three points $p_1=(0,0),p_2=(1∕3,1∕3)$ and $p_3=(2∕3,2∕3)$. The arrangement stratifies the torus into three $0$-faces, six $1$-faces and three $2$-faces. This is not a regular subdivision of the torus since the closure of every $2$-face is a cylinder. Fig. 1 shows the arrangement together with the associated intersection poset.

Fig. 1 A toric arrangement in ${\mathbb{T}}^2$.

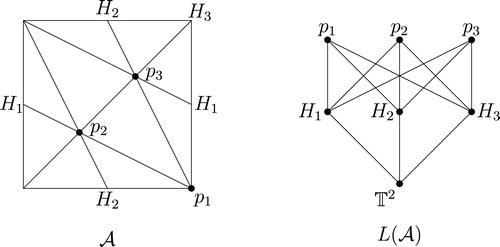
Example 11

Now consider the arrangement formed by including the projection of the line $y=x$ in the previous arrangement. They intersect in the same three points as above but now there are nine $1$-faces and six $2$-faces. The induced stratification is a regular $\Delta$-complex. Fig. 2 shows the arrangement and the associated intersection poset.

Fig. 2 A toric arrangement with regular cell decomposition.

Since our focus is on counting the number of various-dimensional faces of a toric arrangement we now turn to the combinatorial aspect. The idea that captures the combinatorics of the intersections is the Möbius function of the arrangement which we now define.

Definition 12

The Möbius function of a toric arrangement is the function $\mu :L\left(\mathcal{A}\right)\times L\left(\mathcal{A}\right)\to \mathbb{Z}$ defined recursively as follows: $\mu (X,Y)= \begin{array}{cc}1,\hfill & \text{if}X=Y,\hfill \\ -\sum _{X\le Z<Y}\mu (X,Z),\hfill & \text{if}X<Y,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$

The Möbius function plays an important role in counting the number of faces of an arrangement. The following theorem has appeared in [6, Corollary 3.12], [7, Theorem 3] and [8, Example 5.5].

Theorem 13

Let $f_k$ denote the number of $k$-dimensional faces of a toric arrangement $\mathcal{A}$. Then we have $f_k=\sum _{\genfrac{}{}{0ex}{}{dimY=k}{dimZ=0Y\le Z}}\mu (Y,Z).$

In this paper we focus on toric arrangements that arise in the context of crystallographic root systems. Moreover, there is a natural action of a Weyl group associated with these arrangements. The main theorem relates the face numbers of a toric Weyl arrangement to indices of certain subgroups.

3 Linear and toric Weyl arrangements

Recall that a finite reflection group acts naturally on a vector space by fixing reflecting hyperplanes. This forms an interesting class of hyperplane arrangements and the group theoretic data plays an important role in their study. We begin by a quick survey of root systems, finite and affine Weyl groups. We follow Humphrey’s book [13, Chapters 1, 4].

Let $V$ be a real vector space of dimension $l$ endowed with a positive definite symmetric bilinear form $〈v,v^{\prime }〉$. For a vector $\alpha \in V$ the reflection across the linear hyperplane orthogonal to $\alpha$ is given by the formula $s_{\alpha }\left(v\right)=v-\frac{2〈\alpha ,v〉}{〈\alpha ,\alpha 〉}\alpha .$Denote by $H_{\alpha }$ the codimension-$1$ subspace fixed by $s_{\alpha }$.

Definition 14

A finite set $\Phi$ of non-zero vectors in $V$ is called a root system if it satisfies the following conditions:

(R1)	$\Phi \cap \mathbb{R}\alpha =\alpha ,-\alpha \forall \alpha \in \Phi$;

(R2)	$s_{\alpha }\left(\Phi \right)=\Phi \forall \alpha \in \Phi$.

The elements of $\Phi$ are called roots.

Unless otherwise stated we assume that a root system $\Phi$ is essential, i.e., it spans $V$. For a given a root system $\Phi$ the group generated by the reflections $s_{\alpha }\mid \alpha \in \Phi$ is a finite reflection group. However, not all the reflections are needed to write down a generating set. A subset $\Delta \subset \Phi$ is a simple system if $\Delta$ is a vector space basis of $V$ and if each root in $\Phi$ is a linear combination of elements of $\Delta$ with coefficients all of the same sign. The corresponding reflections are called simple reflections.

Theorem 15

[13, Section 1.5]

The group $W=〈s_{\alpha }\mid \alpha \in \Phi 〉$ is generated by the simple reflections $s_{\alpha }\mid \alpha \in \Delta$. Moreover, it has the following presentation $W=〈s_1,\dots ,s_l\mid {\left(s_i{s}_j\right)}^{m_{ij}}=1〉,$where $s_i=s_{{\alpha }_i}\in \Delta$ and $m_{ij}$ is the order of $s_i{s}_j$.

3.1 Linear reflection arrangements

The finite reflection group $W$ acts on $V$ via reflections. The set of fixed points of this action is a union of hyperplanes fixed by reflections in $W$.

Definition 16

Given a finite reflection group $W$ corresponding to an essential root system $\Phi$ the reflection arrangement associated to $W$ is ${\mathcal{A}}_W=H_{\alpha }\mid \alpha \in \Phi .$

Since $H_{\alpha }=H_{-\alpha }$ we only need positive roots to define the reflection arrangement. Every face $F$ of a reflection arrangement is a cone over a simplex of dimension $dimF-1$. The action of $W$ is simply-transitive on the set of chambers of ${\mathcal{A}}_W$. In particular, the number of chambers is equal to $W$. If $C$ is any chamber, then $W$ is generated by the reflections across the walls of $C$. The closure $\overline{C}$ is the strict fundamental domain for the $W$ action on $V$. Let $S$ be the set of reflections with respect to the walls of $C$. Then, the stabilizer $W_x$ of a point $x\in \overline{C}$ is the subgroup generated by $S_x≔s\in S\mid sx=x$. In particular, $W_x$ fixes every point of $\overline{F}$, where $F$ is the face containing $x$.

Example 17

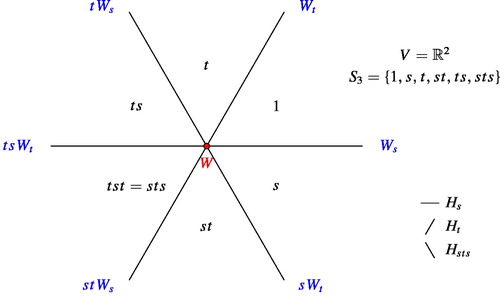
The following is the reflection arrangement corresponding to the symmetric group $S_3$.

Let $\Phi$ be an essential root system. Arbitrarily choose and fix a simple system $\Delta \subset \Phi$. Denote by $S$ the set of generating reflections of $W$. Finally, let ${\mathcal{A}}_W$ be the associated reflection arrangement. The fundamental chamber of ${\mathcal{A}}_W$ is defined as $C≔v\in V\mid s_{\alpha }\left(v\right)>0\forall s_{\alpha }\in S.$For a subset $I\subseteq S$ define $C_I≔v\in \overline{C}\mid s_{\alpha }\left(v\right)=0\forall s_{\alpha }\in I\text{and}{s}_{\alpha }\left(v\right)>0s_{\alpha }\notin I.$Note first that $C=C_{\varnothing }$ and second that the set $C_I$ is a codimension-$I$ face of ${\mathcal{A}}_W$ contained in $\overline{C}$. It is clear that faces ${C_I}_{I\subseteq S}$ partition $\overline{C}$.

As the closure $\overline{C}$ is a strict fundamental domain for the $W$ action given a face $F$ of ${\mathcal{A}}_W$ there exists a $w\in W$ and $J\subset S$ such that $F=w{C}_J.$

Definition 18

Given a subset $I$ of $S$ the subgroup generated by reflections in $I$ is called a parabolic subgroup and is denoted by $W_I$.

Note that $W_I$ is the stabilizer of $C_I$. The following two results are consequences of the theorems proved in [13, Section 1.12, Section 1.15]. However we provide necessary details for the benefit of the reader.

Proposition 19

For each fixed $I\subseteq S$, the faces $w{C}_I$ and $w^{\prime }{C}_I$ are disjoint unless $w,w^{\prime }$ lie in the same left coset of $W_I$, in which case they coincide.

Proof

Fix $I$ and suppose $v\in w{C}_I\cap w^{\prime }{C}_I$. This implies both $w^{-1}v$ and ${w^{\prime }}^{-1}v$ are in $C_I\subseteq \overline{C}$. But the $W$-orbit of $v$ can intersect $\overline{C}$ in only one point. So $w^{-1}v={w^{\prime }}^{-1}v$ which means the element $w^{\prime }{w}^{-1}$ belongs to the isotropy subgroup of $v$. By the definition of $C_I$ and the fact that isotropy subgroup is generated by the reflections fixing it, we deduce that $w{W}_I{w}^{-1}$ is the isotropy subgroup of $v$. So $w^{\prime }{w}^{-1}\in w{W}_I{w}^{-1}$ which implies the conclusion that $w\equiv w^{\prime }\mathrm{mod}{W}_I$. □

Corollary 20

For two disjoint subsets $I$ and $J$ of $S$ the faces $w{C}_I$ and $w^{\prime }{C}_J$ are disjoint.

Theorem 21

The number $f_k$ of $k$-faces of a reflection arrangement ${\mathcal{A}}_W$ are given by the formula: $f_k=\sum _{\genfrac{}{}{0ex}{}{I\subseteq S}{I=l-k}}\frac{W}{W_I}.$

Proof

First note that any $k$-face of ${\mathcal{A}}_W$ is in the $W$-orbit of some $k$-face $C_I$ of $C$, where $I=l-k$. It follows from Proposition 19 that there is a bijection between the faces of ${\mathcal{A}}_W$ labeled $w{C}_I$ and the left cosets $w{W}_I$. Hence the orbit stabilizer theorem implies that the number of faces labeled by $w{W}_I$ is equal to the index of $W_I$ in $W$. Now $f_k$ is obtained by varying $I$ over all the subsets of cardinality $l-k$. □

The following corollary appears in [13, Section 1.11] and is proved using a different argument.

Corollary 22

With the notation as before we have $\sum _{I\subseteq S}{(-1)}^I\frac{W}{W_I}=1.$

Proof

The proof only requires rewriting the left hand side:

$\mathrm{LHS}=\sum _{k=0}^l{(-1)}^k\sum _{\genfrac{}{}{0ex}{}{I\subseteq S}{I=k}}\frac{W}{W_I}={(-1)}^l\sum _{k=0}{(-1)}^{l-k}{f}_{l-k}$

The equality follows from the Euler relation. □

3.2 Toric Weyl arrangements

Since these arrangements arise in the context of affine Weyl groups we quickly revise the relevant details here.

Definition 23

A root system $\Phi$ is called crystallographic if it satisfies in addition to (R1) and (R2) the condition

(R3)	$\frac{2〈\alpha ,\beta 〉}{〈\beta ,\beta 〉}\in \mathbb{Z}\text{for all}\alpha ,\beta \in \Phi .$

Definition 24

Let $\Phi$ be a root system as before, then call ${\alpha }^{\vee }≔\frac{2\alpha }{〈\alpha ,\alpha 〉}$the coroot corresponding to $\alpha \in \Phi$. The set of all coroots ${\Phi }^{\vee }$ is called the dual of $\Phi$; and it is also a root system in $V$.

Affine reflections are defined using coroots. These are involutive affine maps which fix a hyperplane not passing through the origin. The group generated by affine reflections is called a Euclidean reflection group. For $\alpha \in \Phi$ and $k\in \mathbb{Z}$, let $H_{\alpha ,k}≔v\in V\mid 〈v,\alpha 〉=k$denote an affine hyperplane. The corresponding (affine) reflection is given by the formula $s_{\alpha ,k}\left(v\right)=v-(〈v,\alpha 〉-k){\alpha }^{\vee }.$It is easy to see that every affine reflection is a composition of a linear reflection followed by a translation. In particular the following holds: $s_{\alpha ,k}\left(v\right)=s_{\alpha }\left(v\right)+k{\alpha }^{\vee }.$

Definition 25

Let $\Phi$ be an essential crystallographic root system. The group generated by all affine reflections $s_{\alpha ,k}$ with $\alpha \in \Phi$ and $k\in \mathbb{Z}$ is called the affine Weyl group and is denoted by $W_a$.

Similar to the finite case, the $W_a$ action on $V$ defines an affine hyperplane arrangement.

Definition 26

The affine Weyl arrangement $\mathcal{A}\left(W_a\right)$ is defined as follows $\mathcal{A}\left(W_a\right)≔H_{\alpha ,k}\mid \alpha \in \Phi ,k\in \mathbb{Z}.$

This hyperplane arrangement is clearly invariant under the $W_a$ action. The arrangement stratifies $V$ into open and bounded convex subsets called faces. In this case the codimension-$0$ faces are called alcoves. The $W_a$ action on alcoves is simply transitive. For an alcove $C$, the codimension-$1$ faces of its closure $\overline{C}$ are called walls of $C$. Arbitrarily choose and fix a chamber $C$ and let $\tilde{S}$ be the set of reflections with respect to the walls of $C$. The group $W_a$ is generated by reflections in $\tilde{S}$. The following theorem summarizes some important properties of these arrangements and its proof can be found in [13, Section 4.3].

Theorem 27

The alcove $\overline{C}$ is an $l$-simplex and is a strict fundamental domain for the action of $W_a$ on $V$. The stabilizer of a point $x\in \overline{C}$ is the standard subgroup of $W_a$ generated by ${\tilde{S}}_x=s\in \tilde{S}\mid s\left(x\right)=s$.

The fundamental alcove is defined by the following inequalities $C≔v\in V\mid s_{\alpha }\left(v\right)>0,\alpha \in \Delta \text{and}{s}_{\tilde{\alpha }}\left(v\right)<1.$Here $\tilde{\alpha }$ is the unique highest root in $\Phi$. The faces of $\overline{C}$ are indexed by proper subsets of $\tilde{S}$. For a proper subset $J⊊\tilde{S}$ $C_J≔ \begin{array}{c}v\in V\mid s_{\alpha }\left(v\right)=0,s_{\alpha }\in J,s_{\alpha }\left(v\right)>0,s_{\alpha }\notin J,s_{\tilde{\alpha }}\left(v\right)<1\text{if}\tilde{\alpha }\notin J;\hfill \\ v\in V\mid s_{\alpha }\left(v\right)=0,s_{\alpha }\in J\setminus \tilde{\alpha },s_{\alpha }\left(v\right)>0,s_{\alpha }\notin J,s_{\tilde{\alpha }}\left(v\right)=1\text{if}\tilde{\alpha }\in J.\hfill \end{array}$Since $\overline{C}$ is the strict fundamental domain for $W_a$ action the faces of $\mathcal{A}\left(W_a\right)$ are labeled by $w{C}_J$ for $w\in W_a$ and for some face $C_J$ of the fundamental alcove. It is not hard to verify that each reflection in $J$ fix $C_J$.

For the affine Weyl group $W_a$ let $W$ denote the subgroup generated by linear reflections, i.e., reflections of the form $s_{\alpha ,0}$. Then structure of $W_a$ can be explained in terms of $W$ and a lattice in $V$.

Theorem 28

There are points $v\in V$ such that their stabilizer subgroup is isomorphic to $W$. Moreover, there is a surjection $W_a\twoheadrightarrow W$ such that the kernel is isomorphic to the lattice $L\left({\Phi }^{\vee }\right)$ generated by coroots and we have the following semi-direct product structure: $W_a\cong L\left({\Phi }^{\vee }\right)⋊W.$

Since the root system is essential the translation subgroup is isomorphic to ${\mathbb{Z}}^l$, the free abelian group of rank $l$. The non-identity elements of $L\left({\Phi }^{\vee }\right)$ act by translation and consequently have no fixed points. Moreover this action also preserves the arrangement $\mathcal{A}\left(W_a\right)$. The quotient $V∕L\left({\Phi }^{\vee }\right)$ is homeomorphic to the compact torus ${\mathbb{T}}^l={\left(S^1\right)}^l$. We call this torus the coroot torus. The $L$-orbits of the affine hyperplanes in $\mathcal{A}\left(W_a\right)$ define a toric arrangement in ${\mathbb{T}}^l$. Two hyperplanes $H_{\alpha ,k}$ and $H_{\alpha ,m}$ in $\mathcal{A}\left(W_a\right)$ define the same toric hyperplane in the coroot torus if and only if one is a translate of the other by a coroot. In particular, we have the following two situations:

(1) $H_{\alpha ,k}=H_{\alpha ,0}+\frac{k}{2}{\alpha }^{\vee };$(1) (2) $H_{\beta ,1}=H_{\beta ,0}+{\gamma }^{\vee }.$(2)

For a hyperplane $H_{\alpha ,k}$ of $\mathcal{A}\left(W_a\right)$ let $\overline{H_{\alpha ,k}}$ denote its image in the coroot torus.

Definition 29

Given an affine Weyl group $W_a$ and the corresponding root system $\Phi$ the toric Weyl arrangement is the following collection of toric hyperplanes in the coroot torus ${\mathcal{A}}^t\left(W_a\right)≔\overline{H_{{\alpha }_i,k_i}}\mid {\alpha }_i\in \Phi ,k_i\in \mathbb{Z}∕2\mathbb{Z}.$

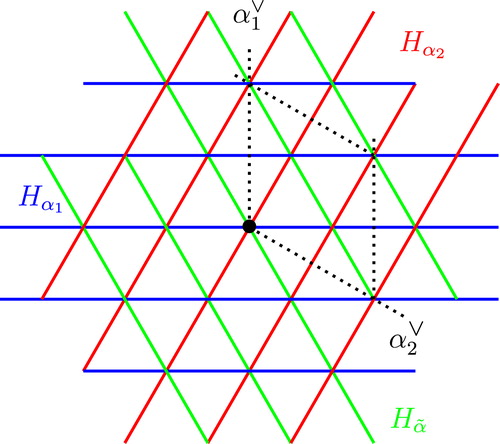
Example 30

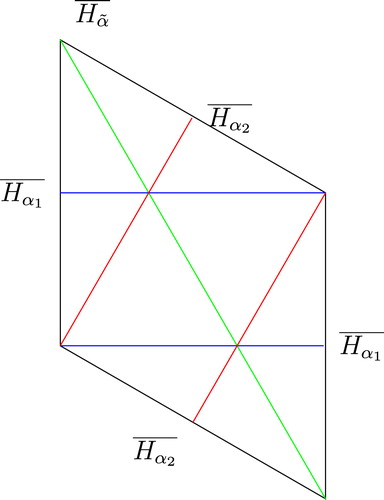
Consider the affine Weyl group of type ${\tilde{A}}_2$; it is isomorphic to ${\mathbb{Z}}^2⋊S_3$ ($S_3$ is the symmetric group on three letters). Its reflection action on ${\mathbb{R}}^2$ fixes three families of parallel lines. Fig. 3 shows the reflecting hyperplanes and the simple coroots.

In Fig. 4 the toric Weyl arrangement of type ${\tilde{A}}_2$ is drawn in the fundamental parallelogram.

Fig. 3 The affine arrangement of type ${\tilde{A}}_2$.

Fig. 4 The toric Weyl arrangement of type ${\tilde{A}}_2$.

4 The face counting formula

In order to relate the face numbers with the indices of parabolic subgroups it is convenient to consider a different fundamental domain.

Proposition 31

The coroot torus $V∕L\left({\Phi }^{\vee }\right)$ can be identified with the $W$-orbits of the closed fundamental alcove $\overline{C}$.

Proof

Pick a point $y\in C$. Then the set $U_y≔x-y\mid \forall x\in C$ is an open neighborhood of the origin homeomorphic to $C$. Observe that $U_y\cap L\left({\Phi }^{\vee }\right)=0$ since all the translates are disjoint. Since the closed alcove $\overline{C}$ is a strict fundamental domain for the $W_a$-action, every point of $V$ is equivalent modulo $L\left({\Phi }^{\vee }\right)$ to the compact set ${\bigcup }_{w\in W}w\overline{C}$. □

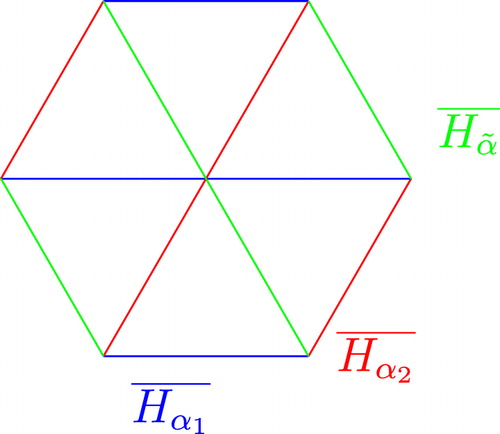
Example 32

We redraw the toric Weyl arrangement of type ${\tilde{A}}_2$ with the new fundamental domain. Fig. 5 shows the arrangement; here the coroot torus is obtained by identifying opposite edges of a regular hexagon.

Fig. 5 The toric Weyl arrangement of type ${\tilde{A}}_2$.

Similar to the finite case one can define parabolic subgroups of $W_a$. Let $J$ be a subset of $\tilde{S}$ and $W_J$ be the subgroup generated by reflections in $J$. Then $W_J$ is finite if and only if $J\ne \tilde{S}$. Moreover, in this case $W_J$ stabilizes $C_J$ (see [13, Sections 4.7, 4.8]).

Theorem 33

The number $f_k$ of $k$-faces of ${\mathcal{A}}^t\left(W_a\right)$ are given by the formula $f_k=\sum _{\genfrac{}{}{0ex}{}{J⊊\tilde{S}}{J=l-k}}\frac{W}{W_J}.$

Proof

The proof is similar to that of Theorem 21. First recall that there exactly $l+1$ reflections in $\tilde{S}$. Now note that faces of ${\mathcal{A}}^t\left(W_a\right)$ are labeled by $w{C}_J$, where $w\in W$ and $C_J$ is a face of $\overline{C}$. Consequently, they are in bijection with left cosets $w{W}_J$. Now apply the orbit stabilizer theorem. □

4.1 The Dehn–Sommerville relations

Since the Euler characteristic of a positive-dimensional torus is $0$ the face numbers of a toric arrangement satisfy the following relation: $\sum _{i=0}^n{(-1)}^i{f}_i=0.$However, this relation does not provide a complete characterization of face numbers. In this section we prove a necessary condition that is satisfied by the face numbers of a toric Weyl arrangement.

We say that a toric arrangement is simplicial if the induced stratification is that of a $\Delta$-complex. Note that a simplicial arrangement need not define the structure of a simplicial complex on the torus. For example, the arrangement in Example 11 is a simplicial arrangement such that the resulting stratification is not a simplicial complex. The arrangement consisting of the line $y=x$ is also simplicial however the stratification is not even regular.

Face numbers of simplicial polytopes satisfy special kind of relations known as the Dehn–Sommerville relations [2, Section 9.2]. It was shown by Klee in [14] that similar relations are satisfied by simplicial complexes that arise as triangulations of closed manifolds.

Theorem 34

Let $K$ be a simplicial complex homeomorphic to a closed $l$-manifold and let $f_i$ denote the number of $i$-simplices. Then the face numbers of $K$ satisfy the following Dehn–Sommerville relations (3) $f_i=\sum _{j=i}^l{(-1)}^{j+l}\left(\genfrac{}{}{0ex}{}{j+1}{i+1}\right)f_j,$(3) for $i=0,1,\dots ,l$.

Define an $(l+1)\times (l+1)$ upper triangular, integer matrix $D=\left(d_{ij}\right),0\le i,j\le l$ as follows $d_{ij}={(-1)}^{j+l}\left(\genfrac{}{}{0ex}{}{j+1}{i+1}\right).$The face vector of $K$ is an $l$-tuple $\mathbf{f}≔(f_0,\dots ,f_l)$ whose components are face numbers of $K$. Then Eq. (3(3) $f_i=\sum _{j=i}^l{(-1)}^{j+l}\left(\genfrac{}{}{0ex}{}{j+1}{i+1}\right)f_j,$(3) ) can be rewritten as $\mathbf{f}=D\mathbf{f}$.

Lemma 35

Let $K$ be a non-regular $\Delta$-complex. Then its first barycentric subdivision is a regular $\Delta$-complex and the second subdivision is a simplicial complex.

Proof

See [15, Section 10.3]. □

In view of the above lemma we need to show that the Dehn–Sommerville relations remain invariant under barycentric subdivision. As a first step we figure out a relationship between the face numbers of an $l$-dimensional $\Delta$-complex $K$, and the face numbers of its barycentric subdivision. Denote by ${\mathbf{f}}^{\prime }$ the face vector of the barycentric subdivision $\mathrm{sd}\left(K\right)$.

Lemma 36

Let $B=\left(b_{ij}\right),0\le i,j\le l$ be an $(l+1)\times (l+1)$ integer matrix with the entries $b_{ij}=\sum _{k=0}^i{(k-i-1)}^{k+j+1}\left(\genfrac{}{}{0ex}{}{i+1}{k}\right)$Then ${\mathbf{f}}^{\prime }=B\mathbf{f}$.

Proof

See [16, Lemma 2.1]. Note that since $b_{ii}=(i+1)!$ the matrix $B$ is invertible. □

Theorem 37

If the face vector ${\mathbf{f}}^{\prime }$ of the subdivision $\mathrm{sd}\left(K\right)$ satisfies Dehn–Sommerville relations then so does the face vector $f$ of $K$.

Proof

First observe that $BD=DB$. Now the proof is straightforward.

${\mathbf{f}}^{\prime }=D{\mathbf{f}}^{\prime }$$B\mathbf{f}=DB\mathbf{f}=BD\mathbf{f}.\square$

Corollary 38

The face numbers of a toric Weyl arrangement satisfy the Dehn–Sommerville relations.

Notes

Peer review under responsibility of Kalasalingam University.