Specified holes with pairwise disjoint interiors in planar point sets

Abstract

A $k$-hole of a planar point set in general position is a convex $k$-gon whose vertices are elements of the set and whose interior contains no elements of the set. We discuss the minimum size of a point set that contains specified holes with disjoint interiors.

Keywords:

• The Erdős–Szekeres theorem
• Empty convex polygons
• Disjoint holes

1 Introduction

In 1935, Erdős and Szekeres [1] stated that for every integer $t\ge 3$ there is a smallest number $f\left(t\right)$ such that every set of at least $f\left(t\right)$ points in general position in the plane, contains a subset of points that are the vertices of a convex $t$-gon. The exact value of $f\left(t\right)$ is a long standing open problem. A construction due to Erdős and Szekeres [2] shows that $f\left(t\right)\ge 2^{t-2}+1$, which is also conjectured to be sharp. It is known that $f\left(4\right)=5,f\left(5\right)=9$ [3] and $f\left(6\right)=17$ [4]. The best known upper bound is due to Tóth and Valtr [5], $f\left(t\right)\le \left(\genfrac{}{}{0ex}{}{2t-5}{t-3}\right)+1$. For a more detailed description of the Erdős and Szekeres theorem and its many ramifications, see the surveys by Bárány and Károlyi [6] and Morris and Soltan [7].

Erdős [8] also asked the following combinatorial geometry problem in 1979: Find the smallest integer $n\left(k\right)$ such that any set of $n\left(k\right)$ points in general position in the plane, contains the vertices of a convex $k$-gon, whose interior contains no points of the set. Such a subset is called an empty convex k-gon or a $k$-hole of the set. Klein [1] found $n\left(4\right)=5$, and $n\left(5\right)=10$ was determined by Harborth [9]. Horton [10] constructed arbitrarily large point sets which do not contain any 7-holes, so $n\left(k\right)$ does not exist for $k\ge 7$. For the remaining case of $n\left(6\right)$, Overmars exhibited a set of $29$ points, the largest known, with no empty convex hexagons [11]. About 10 years ago, the existence of $n\left(6\right)$ was proved by Gerken [12] and independently by Nicolás [13]. Later, Valtr [14] gave a similar version of Gerken’s proof. And recently, Koshelev improved the upper bound to $n\left(6\right)\le 463$ [15]. Therefore the current record of $n\left(6\right)$ is $30\le n\left(6\right)\le 463$.

Fig. 1(a) n(4, 4) ≥ 9.

Fig. 1(b) m(4, 4) ≥ 7.

A pair of holes is said to be disjoint if their convex hulls do not intersect. We denote $n(k,l)$ for $k\le l$ by the smallest integer such that any set of $n(k,l)$ points in general position in the plane, contains both a $k$-hole and an $l$-hole that are disjoint. Clearly, $n(3,3)=6$ and Horton’s result implies that $n(k,l)$ does not exist for all $l\ge 7$. For this function, we showed $n(3,4)=7$ [16] and $n(4,4)=9$ in [17], and also determined $n(3,5)=10,12\le n(4,5)\le 13$ and $17\le n(5,5)\le 20$ in [20] later tightened to $n(4,5)=12$ and also improved the upper bound of $n(5,5)$ to 19 [21].

In [19], we considered several problems for disjoint holes. Let $n(k_1,k_2,\dots ,k_l)$ be the smallest integer such that any set of $n(k_1,\dots ,k_l)$ points contains a $k_i$-hole for each $i$, $1\le i\le l$, where the holes are pairwise disjoint. We showed that $n(2,3,4)=9,n(2,3,5)=11,n(3,4,4)=12,n(4,4,4)=14,15\le n(4,4,5)\le 17$ and more. In particular, any set of $15$ points in general position in the plane is partitioned into a 1-hole, a 2-hole, a 3-hole, a 4-hole and a 5-hole which are pairwise disjoint, that is $n(1,2,3,4,5)=15$.

In this paper, the related problem is considered as follows. A family of holes is with disjoint interiors if their interiors are pairwise disjoint. We define $m(k,l)$ for $k\le l$ by the smallest integer such that any set of $m(k,l)$ points in general position in the plane contains both a $k$-hole and an $l$-hole with disjoint interiors. Clearly, $m(k,l)\le n(k,l)$ holds for any $k,l$, and also $m(k,l)$ does not exist for all $l\ge 7$ by Horton’s result.

For example, an 8-point set in Fig. 1(a) does not contain two disjoint 4-hole, implying that $n(4,4)\ge 9$. However, it contains two holes with disjoint interiors, formed by $\{v_1,p_{1,2},p_{3,4},p_{4,1}\}$ and $\{v_2,p_{2,3},p_{3,4},p_{1,2}\}$. And Fig. 1(b) shows $m(4,4)\ge 7$, that is, this 6-point set has no two 4-holes with disjoint interiors. We discuss two specified holes in Section 3 and three specified holes in Section 4.

2 Preliminaries

2.1 Notations and definitions

We first give notations and definitions used in the proofs. Throughout this work, we consider only planar point sets in general position. For such a point set $P$, we distinguish the vertices $V\left(P\right)$ on the convex hull boundary from the remaining interior points $I\left(P\right)$. Let $V\left(P\right)=\{v_1,v_2,\dots ,v_t\}$ in clockwise order. We remark that when indexing a set of $t$ points, we identify indices modulo $t$. If $I\left(P\right)=\varnothing$, the convex $t$-gon formed by $V\left(P\right)$ is called empty. A line segment $\overline{v_i{v}_{i+1}}$ is simply called an edge of $V\left(P\right)$. Let $R$ be a closed region in the plane. A point of $P$ in the interior of $R$ is generally said to be an interior point of $R$, and $R$ is empty if it contains no interior points.

We denote the closed convex cone by $\gamma (a;b,c)$ or $\gamma (a;c,b)$ such that $a$ is the apex and $b$ and $c$ lie on the boundary. If $\gamma (a;b,c)$ is not empty, we define an attack point $\alpha (a;b,c)$ as the interior point of $\gamma (a;b,c)$ such that $\gamma (a;b,\alpha (a;b,c))$ is empty. A quasi-attack point $\tilde{\alpha }(a;b,c)$ in $\gamma (a;b,c)$ is the point $c$ or $\alpha (a;b,c)$ if $\gamma (a;b,c)$ is empty or not, respectively. For $\delta =b$ or $c$ of $\gamma (a;b,c)$, let ${\delta }^{\prime }$ be a point collinear with $a$ and $\delta$ so that $a$ lies on the line segment $\overline{\delta {\delta }^{\prime }}$. Then we can consider a convex cone of $\gamma (a;b,c^{\prime })$ or $\gamma (a;b^{\prime },c)$.

Let $l(a,b)$ be the line through $a$ and $b$. Denote the closed half-plane bounded by the line $l(a,b)$ that contains $c$ or does not contain $c$ by $H(ab;c)$ or $H(ab;\overline{c})$, respectively. For any elements $a,b,c$ of $P$, we let $P_1$ or $P_2$ be a subset of $P$ on $H(ab;c)$ or $H(ab;\overline{c})$, respectively, where $P_1\cap P_2=\{a,b\}$. Then we say that the cutting line $l(a,b)$ divides $P$ into $P_1$ and $P_2$.

An interior point $p_{i,i+1}$ of $P$ is said to be a friend to the edge $\overline{v_i{v}_{i+1}}$ of $V\left(P\right)$ if $\gamma (v_i;v_{i+1},p_{i,i+1})\cup \gamma (v_{i+1};v_i,p_{i,i+1})$ is empty, e.g. Fig. 1(a). We represent a $k$-hole $H$ by $H={(v_1\cdots v_k)}_k$ if $V\left(H\right)=\{v_1,\dots ,v_k\}$ is in clockwise order.

2.2 Lemmas

We now present two lemmas used throughout the paper. Let $P$ be a set of $n$ points for $n\ge 4$, and $V\left(P\right)=\{v_1,\dots ,v_t\}$ in clockwise order.

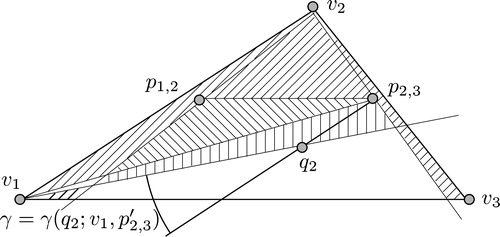
Lemma 1

If there exists an edge of $V\left(P\right)$ with no friend, then we have a cutting line which divides $P$ into a 4-hole and the remaining $n-2$ points.

Proof

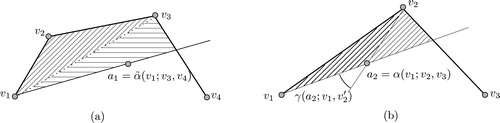
We consider any edge of $V\left(P\right)$, say $\overline{v_1{v}_2}$. First, if $△v_1{v}_2{v}_3$ is empty, then $\overline{v_1{v}_2}$ has no friend. For the quasi-attack point $a_1=\tilde{\alpha }(v_1;v_3,v_4)$, there exists a cutting line $l(v_1,a_1)$ which divides $P$ into a 4-hole of ${\left(v_1{v}_2{v}_3{a}_1\right)}_4$ and the remaining $n-2$ points, see Fig. 2 (a).

If $△v_1{v}_2{v}_3$ is not empty, there is an attack point $a_2=\alpha (v_1;v_2,v_3)$, see Fig. 2 (b). We remark that if the convex cone $\gamma (a_2;v_1,v_2^{\prime })$ is empty, then $a_2$ is the friend to the edge $\overline{v_1{v}_2}$. Otherwise, for $a_3=\alpha (a_2;v_1,v_2^{\prime })$, there exists a cutting line $l(a_2,a_3)$ which divides $P$ into a 4-hole of ${\left(v_1{v}_2{a}_2{a}_3\right)}_4$ and the $n-2$ points.

Fig. 2 Shaded areas are empty.

We remark that for any $i$, a friend $p_{i,i+1}$ must lie in $\gamma (v_i;v_{i+1},v_{i+2})\cap \gamma (v_{i+1};v_i,v_{i-1})$. Thus, any pair of consecutive edges does not have a common friend except for the case in which $\left|P\right|=4$ and $\left|V\left(P\right)\right|=3$. If $\left|V\left(P\right)\right|>\left|I\left(P\right)\right|$, then there exists an edge of $V\left(P\right)$ having no friend. Therefore we give the next lemma.

Lemma 2

If $\left|V\left(P\right)\right|>\left|I\left(P\right)\right|$, then we have a cutting line which divides $P$ into a 4-hole and the remaining $n-2$ points.

3 Two holes with disjoint interiors

In this section, we discuss values of $m(k,l)$, that is we consider two holes with disjoint interiors. If $k=3$, then the values are easily shown. For example, any set of four points has a 3-hole of $T={\left(abc\right)}_3$ and the remaining point $p$. Since $p$ can see some edge of $T$, say $\overline{ab}$, we obtain another 3-hole of ${\left(abp\right)}_3$ such that these two holes are with disjoint interiors. Thus,

Proposition 1

$m(3,3)=4$.

Using $n\left(4\right)=5$, any set of five points has a 4-hole. The remaining point can also see some edge of the 4-hole. Thus,

Proposition 2

$m(3,4)=5$.

The next result is clearly shown by $n\left(5\right)=10$.

Proposition 3

$m(3,5)=10$.

The next result shows that a set of seven points has two 4-holes with disjoint interiors, and the value is tight.

Theorem 1

$m(4,4)=7$.

Proof

Fig. 1(b) shows the lower bound of $m(4,4)\ge 7$. To prove the upper bound, let $P$ be a set of seven points. If $\left|V\left(P\right)\right|\ge 4$, there exists a cutting line dividing $P$ into a 4-hole and the remaining 5-point set $S$ by Lemma 2. Then we can find another 4-hole of $S$ using $n\left(4\right)=5$.

The remaining case is for $\left|V\left(P\right)\right|=3$. If there is an edge having no friend, we have a desired cutting line dividing into a 4-hole and the 5-point set containing another 4-hole by Lemma 1. Otherwise, there are three friends $p_{i,i+1}$ to each edge $\overline{v_i,v_{i+1}}$ of $V\left(P\right)=\{v_1,v_2,v_3\}$. Denote $T_i=△p_{i-1,i}{v}_i{p}_{i,i+1}$ for $i=1,2,3$. If the remaining point $p$ lies in some $T_i$, say $T_2$, we obtain two 4-holes of ${\left(p{p}_{3,1}{v}_1{p}_{1,2}\right)}_4$ and ${\left(p{p}_{2,3}{v}_3{p}_{3,1}\right)}_4$ with disjoint interiors. If $p$ lies in $△p_{1,2}{p}_{2,3}{p}_{3,1}$, we also obtain ${\left(p{p}_{3,1}{v}_1{p}_{1,2}\right)}_4$ and ${\left(p{p}_{2,3}{v}_3{p}_{3,1}\right)}_4$.

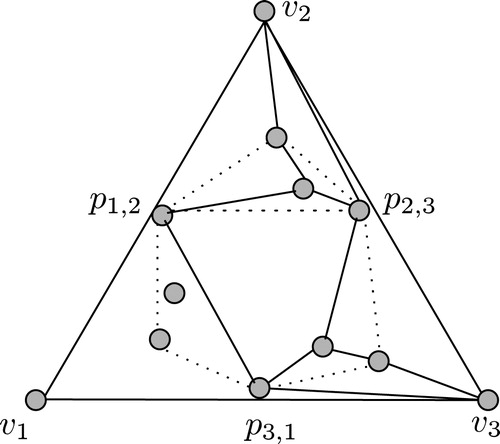
The next result is a set of ten points has a 4-hole and a 5-hole with disjoint interiors, and the value is tight. Since a 10-point set has a 5-hole, we consider configurations of the remaining five points to prove the upper bound.

Theorem 2

$m(4,5)=10$.

Proof

Any set of ten points has a 5-hole by $n\left(5\right)=10$, so $m(4,5)\ge 10$. To prove $m(4,5)\le 10$, let $F={\left(v_1{v}_2{v}_3{v}_4{v}_5\right)}_5$ be a 5-hole of a given 10-point set and consider the closed convex cones ${\gamma }_i=\gamma (v_i;v_{i-1}^{\prime },v_{i+1})$ for $1\le i\le 5$. Without loss of generality, we assume that ${\gamma }_1$ contains the largest number of interior points of all the ${\gamma }_i$’s. Let $I\left({\gamma }_i\right)$ be a set of interior points of ${\gamma }_i$ for any $i$, and we have three cases according to the number of $I\left({\gamma }_1\right)$.

Case 1: $\left|I\left({\gamma }_1\right)\right|\ge 3$. Since there are at least five points on ${\gamma }_1$, we have $F$ and a 4-hole on ${\gamma }_1$ by $n\left(4\right)=5$.

Case 2: $\left|I\left({\gamma }_1\right)\right|=2$. If $\gamma (v_1;v_5^{\prime },v_2^{\prime })$ is not empty, we have $F$ and a 4-hole on $H(v_1{v}_2;\overline{v_5})$. And more if ${\gamma }_5$ is not empty, there exist ${\left(v_1{v}_3{v}_4{v}_5\alpha (v_5;v_1,v_4^{\prime })\right)}_5$ and a 4-hole on $\gamma (v_1;v_3,v_5^{\prime })$. Thus, we consider the case in which ${\gamma }_5$ is empty. By the same way, ${\gamma }_3\setminus \gamma (v_4;v_3^{\prime },v_5^{\prime })$ is also empty, see Fig. 3. We have three subcases.

(a) $\left|I\left({\gamma }_2\right)\right|=0$: We obtain $F$ and a 4-hole on $H(v_4{v}_5;\overline{v_1})$.

(b) $\left|I\left({\gamma }_2\right)\right|=1$: If $I\left({\gamma }_1\right)$ lies in $\gamma (v_2;v_3^{\prime },v_1^{\prime })$, we have $F$ and a 4-hole on $H(v_2{v}_3;\overline{v_1})$. Otherwise, we have a 6-hole of ${\left(v_{1}w{v}_2{v}_3{v}_4{v}_5\right)}_6$ for some point $w$ of $I\left({\gamma }_1\right)$. Then if $\gamma (v_2;v_3,v_4)$ is empty, we obtain ${\left(v_{1}w{v}_2{v}_3{v}_4\right)}_5$ and a 4-hole on $\gamma (v_4;v_2^{\prime },v_1)$. If not so, we obtain ${\left(v_{1}w{v}_2{v}_4{v}_5\right)}_5$ and a 4-hole on $\gamma (v_2;v_1^{\prime },v_4)$.

(c) $\left|I\left({\gamma }_2\right)\right|=2$: If $\gamma (v_2;v_3^{\prime },v_1^{\prime })$ is not empty, we obtain $F$ and a 4-hole on $H(v_2{v}_3;\overline{v_1})$. Otherwise, we have a 5-hole of ${\left(v_{1}w{v}_2{v}_4{v}_5\right)}_5$ for some point $w$ of $I\left({\gamma }_1\right)$ and a 4-hole on $\gamma (v_2;v_1^{\prime },v_4)$.

Case 3: $\left|I\left({\gamma }_i\right)\right|=1$ for each $i$. Let $w_i$ be precisely one interior point of ${\gamma }_i$.

(a) $w_1$ lies on $H(v_2{v}_3;v_1)$: Clearly, we have a 6-hole ${\left(v_1{w}_1{v}_2{v}_3{v}_4{v}_5\right)}_6$. If $w_3$ lies in $\gamma (v_2;v_3,v_4)$, we have ${\left(v_1{w}_1{v}_2{v}_4{v}_5\right)}_5$ and ${\left(w_3{v}_4{v}_2{v}_3\right)}_4$. Otherwise, we have ${\left(v_1{w}_1{v}_2{v}_3{v}_4\right)}_5$ and a 4-hole on $\gamma (v_4;v_2^{\prime },v_1)$.

(b) $w_1$ lies on $H(v_2{v}_3;\overline{v_1})$: If $w_2$ lies on $H(v_3{v}_4;v_2)$, we have a 6-hole ${\left(v_1{v}_2{w}_2{v}_3{v}_4{v}_5\right)}_6$ and we are done by the same way as in (a). Hence, $w_2$ lies on $H(v_3{v}_4;\overline{v_2})$. If $w_2$ is not contained in $△v_2{w}_1{v}_3$, we have $F$ and ${\left(v_3{v}_2{w}_1{w}_2\right)}_4$. Otherwise, we obtain $F$ and ${\left(v_3{w}_2{w}_1{w}_3\right)}_4$.

Fig. 3 Illustration of Case 2.

We next consider the case of two 5-holes with disjoint interiors. The upper bound is showed by the simple way using $n\left(5\right)=10$.

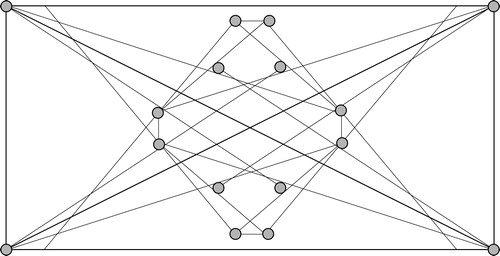
Theorem 3

$14\le m(5,5)\le 18$.

Proof

A 13-point set as shown in Fig. 4 gives $m(5,5)\ge 14$. To prove the upper bound, we consider an 18-point set, and let $v_1,v_2$ and $v_3$ be three consecutive vertices of the set. Then there exists an interior point $p$ such that each of $\gamma (v_2;v_1,p)$ and $\gamma (v_2;p,v_3)$ contains exactly ten points and it has a 5-hole by $n\left(5\right)=10$.

Fig. 4 $m(5,5)\ge 14$.

4 Three holes with disjoint interiors

In this section, we discuss the cases of three holes with disjoint interiors. Let $m(k_1,k_2,k_3)$ denote the smallest integer such that any set of $m(k_1,k_2,k_3)$ points contains a $k_1$-hole, a $k_2$-hole and a $k_3$-hole with disjoint interiors. We first consider some cases of $m(3,k,l)$ for $3\le k\le l\le 5$.

Proposition 4

$m(3,3,3)=5,m(3,3,4)=6,m(3,3,5)=10,m(3,4,4)=7,m(3,4,5)=10$.

Proof

Let $P$ be a set of $m(3,k,l)$ points. If $P$ has a $k$-hole, an $l$-hole and the remaining points $S$, then some point $p$ of $S$ can see some edge of these holes. Therefore,

(i) $m(3,3,3)=5$ holds by $m(3,3)=4$, (ii) $m(3,3,4)=6$ holds by $m(3,4)=5$,

(iii) $m(3,3,5)=10$ holds by $m(3,5)=10$, and (iv) $m(3,4,5)=10$ holds by $m(4,5)=10$.

We show $m(3,4,4)=7$. By $m(4,4)=7$, if the remaining point exists, the point sees some edge of 4-holes. Otherwise, two 4-holes have only the common vertex $p$, namely ${\left(v_1{v}_2{v}_{3}p\right)}_4$ and ${\left(u_1{u}_2{u}_{3}p\right)}_4$. Then we have a 3-hole of ${\left(v_{1}p{u}_3\right)}_3$ or ${\left(u_{1}p{v}_3\right)}_3$. Hence we can show the existence of desired holes.

The next result shows a set of nine points has three 4-holes with disjoint interiors, and this value is tight.

Theorem 4

$m(4,4,4)=9$.

Proof

The lower bound of $m(4,4,4)$ realizes an 8-point set as shown in Fig. 1(a), so $m(4,4,4)\ge 9$.

To prove the upper bound, let $P$ be a set of nine points. We have the cases according to the number of vertices of $P$. If $\left|V\left(P\right)\right|\ge 5$, there exists a cutting line dividing $P$ into a 4-hole and the remaining 7-point set $S$ by Lemma 2. Then we have two 4-holes of $S$ using $m(4,4)=7$.

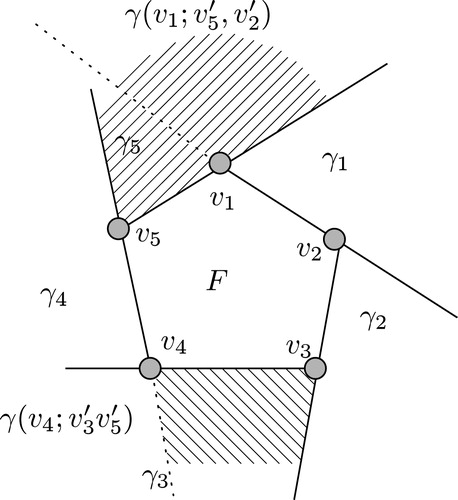
Case 1: $\left|V\left(P\right)\right|=4$. If an edge of $V\left(P\right)$ has no friend, we have a cutting line dividing into a 4-hole and the remaining seven points by Lemma 1, and we are done by $m(4,4)=7$.

Otherwise, every edge of $P$ has its friend. Let $V\left(P\right)=\{v_1,v_2,v_3,v_4\}$ and $p_{i,i+1}$ is a friend to an edge $\overline{v_i{v}_{i+1}}$ for any $i,1\le i\le 4$. We consider the position of the remaining point $p$ of $P$.

Subcase 1A: $p$ lies in some $T_i=△p_{i-1,i}{v}_i{p}_{i,i+1}$ for $i=1,2,3,4$, say $△p_{1,2}{v}_2{p}_{2,3}$. If $p$ lies in $H(v_2{p}_{4,1};v_1)$, then we have a 4-hole of ${\left(p{p}_{4,1}{v}_1{p}_{1,2}\right)}_4$ and $H(p{p}_{4,1};v_3)$ has seven points. Otherwise, $p$ lies in $H(v_2{p}_{4,1};v_3)$. Then we have ${\left(p{p}_{2,3}{v}_3{p}_{3,4}\right)}_4$, ${\left(p{p}_{3,4}{v}_4{p}_{4,1}\right)}_4$ and ${\left(p{p}_{4,1}{v}_1{p}_{1,2}\right)}_4$.

Subcase 1B: $p$ lies inside the quadrilateral $p_{1,2}{p}_{2,3}{p}_{3,4}{p}_{4,1}$. We obtain ${\left(p_{4,1}{v}_1{p}_{1,2}p\right)}_4$, ${\left(p_{1,2}{v}_2{p}_{2,3}p\right)}_4$ and ${\left(p_{2,3}{v}_3{p}_{3,4}p\right)}_4$ with disjoint interiors.

Case 2: $\left|V\left(P\right)\right|=3$. We only consider the case in which every edge of $V\left(P\right)$ has its friend by Lemma 1. Let $V\left(P\right)=\{v_1,v_2,v_3\}$ and denote $T_i=△p_{i-1,i}{v}_i{p}_{i,i+1}$ for $i=1,2,3$. There are two subcases.

Subcase 2A: Some $T_i$, say $T_2$, is empty.

(i) $△v_1{p}_{1,2}{p}_{2,3}$ is not empty: Since we have $q_1=\alpha (p_{2,3};p_{1,2},v_1)$, there exists a cutting line $l(q_1,p_{2,3})$ dividing into a 4-hole ${\left(p_{1,2}{v}_2{p}_{2,3}{q}_1\right)}_4$ and the remaining seven points.

(ii) $△v_1{p}_{1,2}{p}_{2,3}$ is empty: Since there is $q_2=\alpha (v_1;p_{2,3},p_{3,1})$, we consider the convex cone $\gamma =\gamma (q_2;v_1,p_{2,3}^{\prime })$, see Fig. 5. If $\gamma$ is not empty, for $q_3=\alpha (q_2;v_1,p_{2,3}^{\prime })$ we have a cutting line $l(q_3,q_2)$ dividing into two 4-holes of ${\left(v_1{p}_{1,2}{q}_2{q}_3\right)}_4$ and ${\left(p_{1,2}{v}_2{p}_{2,3}{q}_2\right)}_4$, and the remaining five points. There is a 4-hole of the 5-point set by $n\left(4\right)=5$ and we are done.

If $\gamma$ is empty, $q_2$ is a friend to the edge $\overline{v_1{p}_{2,3}}$ of $V\left(P^{\prime }\right)$ for $P^{\prime }=P\setminus \{v_2,p_{1,2}\}$. We remark that $△v_1{p}_{2,3}{q}_2$ cannot be contained in the convex hull of any 4-hole of $P^{\prime }$. Thus we obtain ${\left(p_{1,2}{v}_2{p}_{2,3}{q}_2\right)}_4$ and two 4-holes of the 7-point set $P^{\prime }$.

Subcase 2B: $T_i$ contains only the point $w_i$ of $P$ for every $i=1,2,3$.

We consider the position of $w_2$. If $w_2$ lies in $H(v_2{w}_1;v_1)$, we have a cutting line $l(w_1,w_2)$ dividing into ${\left(v_1{p}_{1,2}{w}_2{w}_1\right)}_4$ and the 7-point set. Also, by the symmetry, if $w_2$ lies in $H(v_2{w}_3;v_3)$, $l(w_2,w_3)$ is the cutting line. Otherwise, we have three 4-holes of ${\left(p_{1,2}{v}_2{w}_2{w}_1\right)}_4$, ${\left(w_2{v}_2{p}_{2,3}{w}_3\right)}_4$ and ${\left(w_1{w}_2{w}_3{p}_{3,1}\right)}_4$ with disjoint interiors.

Fig. 5 We consider the convex cone $\gamma (q_2;v_1,p_{2,3}^{\prime })$.

We next consider the case of two 4-holes and one 5-hole with disjoint interiors, that is not exact value.

Theorem 5

$11\le m(4,4,5)\le 12$.

Proof

The lower bound realizes a 10-point set $P$ such that $\left|V\left(P\right)\right|=5$ and each edge of $V\left(P\right)$ has its friend. To show $m(4,4,5)\le 12$, let $P$ be a 12-point set. If $\left|V\left(P\right)\right|\ge 7$, there exists a cutting line dividing $P$ into a 4-hole and the remaining 10-point set $S$ by Lemma 2. We have both a 4-hole and a 5-hole of $S$ by $m(4,5)=10$.

For $3\le \left|V\left(P\right)\right|\le 6$, we discuss under the condition in which every edge of $V\left(P\right)$ has its friend by Lemma 1. Recall that $V\left(P\right)={\left\{v_i\right\}}_{i\ge 1}$ in clockwise order and $p_{i,i+1}$ is the friend to an edge $\overline{v_i{v}_{i+1}}$. We consider a triangle $T_i=△p_{i-1,i}{v}_i{p}_{i,i+1}$ for any $i$.

Case 1: Some $T_i$, say $T_2$, is empty.

Subcase 1A: If $△v_1{p}_{1,2}{p}_{2,3}$ is not empty, we have a cutting line $l(q_1,p_{2,3})$ for $q_1=\alpha (p_{2,3};p_{1,2},v_1)$ dividing into a 4-hole ${\left(p_{1,2}{v}_2{p}_{2,3}{q}_1\right)}_4$ and the remaining ten points.

Subcase 1B: $△v_1{p}_{1,2}{p}_{2,3}$ is empty.

(i) $△v_1{p}_{2,3}{v}_3$ is not empty: Since there is $q_2=\alpha (v_1;p_{2,3},v_3)$, we consider $\gamma =\gamma (q_2;v_1,p_{2,3}^{\prime })$. If $\gamma$ is not empty, for $q_3=\alpha (q_2;v_1,p_{2,3}^{\prime })$ we have a cutting line $l(q_3,q_2)$ dividing into a 5-hole of ${\left(v_1{p}_{1,2}{p}_{2,3}{q}_2{q}_3\right)}_5$ and the remaining eight points. There are two 4-hole of the 8-point set by $m(4,4)=7$. If $\gamma$ is empty, since $q_2$ is a friend to $\overline{v_1{p}_{2,3}}$ of $V\left(P^{\prime }\right)$ for $P^{\prime }=P\setminus \{v_2,p_{1,2}\}$, $△v_1{p}_{2,3}{q}_2$ cannot be contained in the convex hull of any 4-hole of $P^{\prime }$. We obtain ${\left(p_{1,2}{v}_2{p}_{2,3}{q}_2\right)}_4$ and both a 4-hole and a 5-hole of the 10-point set $P^{\prime }$.

(ii) $△v_1{p}_{2,3}{v}_3$ is empty: Note that $\left|V\left(P\right)\right|\ge 4$. For $q_3=\tilde{\alpha }(v_1;v_3,v_4)$, we have a cutting line $l(v_1,q_3)$ dividing into ${\left(v_1{p}_{1,2}{p}_{2,3}{v}_3{q}_3\right)}_5$ and the remaining eight points.

Case 2: No $T_i$ is empty for any $i$. Since $\left|P\right|\ge 3\left|V\left(P\right)\right|$, we consider the following two subcases.

Subcase 2A: $\left|V\left(P\right)\right|=4$. Let $w_i$ be only the point of $P$ inside $T_i$ for each $i$. If $w_2$ lies in $H(v_2{w}_1;v_1)$, we have a 4-hole ${\left(w_2{w}_1{v}_1{p}_{1,2}\right)}_4$ and $l(w_1,w_2)$ is the cutting line. Otherwise, $w_2$ is in $H(v_2{w}_1;v_3)$. Then we have ${\left(w_1{p}_{1,2}{v}_2{w}_2\right)}_4$, ${\left(w_2{p}_{2,3}{w}_3{p}_{3,4}\right)}_4$ and ${\left(w_1{w}_2{p}_{3,4}{w}_4{p}_{4,1}\right)}_5$.

Subcase 2B: $\left|V\left(P\right)\right|=3$. There are two cases according to the number of points of $P$ inside $T_i$.

(i) Some $T_i$, say $T_2$ contains only the point $w$: If $△p_{1,2}{p}_{2,3}{v}_1$ is empty, we have a cutting line $l(p_{2,3},q_1)$ for $q_1=\alpha (p_{2,3};v_1,p_{3,1})$ dividing into ${\left(p_{1,2}w{p}_{2,3}{q}_1{v}_1\right)}_5$ and the remaining eight points. If it is not empty, we consider $\gamma =\gamma (q_2;p_{2,3},p_{1,2}^{\prime })$ for $q_2=\alpha (p_{2,3};p_{1,2},v_1)$. Then if $\gamma$ is not empty, we have a cutting line $l(q_3,q_2)$ for $q_3=\alpha (q_2;p_{2,3},p_{1,2}^{\prime })$ dividing into six points containing ${\left(p_{1,2}w{p}_{2,3}{q}_3{q}_2\right)}_5$ and the remaining eight points. If $\gamma$ is empty, then $q_2$ is a friend to $\overline{p_{1,2}{p}_{2,3}}$ of $V\left(P^{\prime }\right)$ for $P^{\prime }=P\setminus \{v_2,w\}$. Hence we obtain ${\left(p_{1,2}w{p}_{2,3}{q}_2\right)}_4$, and a 4-hole and a 5-hole of the 10-point set $P^{\prime }$.

(ii) Every triangle $T_i$ contains exactly two points of $P$: If some $T_i$, say $T_2$ contains $\{w_1,w_2\}$ such that $Q=\{p_{1,2},w_1,w_2,p_{2,3}\}$ is in convex position, for $q_4=\tilde{\alpha }(p_{1,2};p_{2,3},v_3)$ we have a cutting line $l(p_{1,2},q_4)$ dividing into six points containing a 5-hole formed by $Q\cup \left\{q_4\right\}$ and the remaining eight points. Otherwise, we have a configuration as shown in Fig. 6 and we can obtain the desired holes.

Fig. 6 The final configuration in case 2.

5 Conclusions

1. We showed several results for $m(k,l)$. In fact, the condition of integers $k$ and $l$ is for $3\le k\le l\le 6$, so the number of types for $m(k,l)$ are ten cases. However, $30\le n\left(6\right)\le 463$ means that the function $m(k,6)$ is not valid. Therefore, we checked out all the cases of $m(k,l)$ for $l\le 5$.

For a set of three holes, we can easily show the following results by a simple method. Let $v_1,v_2$ be consecutive vertices on the convex hull of a given point set. We consider a point $p$ such that the closed convex cone $\gamma (v_1;v_2,p)$ contains exactly ten points. Then we have a 5-hole on this convex cone by $n\left(5\right)=10$. Therefore, $m(3,5,5)\le 18$, $m(4,5,5)\le m(4,5)+8=18$ and $m(5,5,5)\le m(5,5)+8\le 26$. The lower bounds of $m(3,5,5)$ and $m(4,5,5)$ are shown by $14\le m(5,5)\le m(3,5,5)\le m(4,5,5)$. And the lower bound of $m(5,5,5)$ realizes the configuration as shown in Fig. 7, which implies $n(5,5)\ge 17$.

Fig. 7 $m(5,5,5)\ge 17$.

Proposition 5

$14\le m(3,5,5)\le m(4,5,5)\le 18$, $17\le m(5,5,5)\le 26$.

Hence, for a set of three holes, we estimated all the cases except for $m(k,l,6)$.

2. The following theorem is announced in [22] without proof.

Theorem A

Any point set $P$ with $n=2k+3$ elements in general position contains the vertices of $k$ empty convex quadrilaterals with disjoint interiors.

Using this result, both $m(4,4)=7$ in Theorem 1 and $m(4,4,4)=9$ in Theorem 4 are derived. However, because the proof has been not published for ten years, we prove only our results in this article to introduce a new problem. In addition, we can show that the lower bound of $m(4,4,\dots ,4)$ for $k$ 4-holes is realized in the configuration of a $2k+2$ point set $P$ such that $\left|V\left(P\right)\right|=k+1$ and each edge has its friend. Therefore,

Proposition 6

$m\left(\underset{k}{\underbrace{4,4,\dots ,4}}\right)\ge 2k+3$