The upper domatic number of a graph

Abstract

Let $G=(V,E)$ be a graph. For two disjoint sets of vertices $R$ and $S$, set $R$ dominates set $S$ if every vertex in $S$ is adjacent to at least one vertex in $R$. In this paper we introduce the upper domatic number $D\left(G\right)$, which equals the maximum order $k$ of a vertex partition $\pi =\{V_1,V_2,\dots ,V_k\}$ such that for every $i,j$, $1\le i<j\le k$, either $V_i$ dominates $V_j$ or $V_j$ dominates $V_i$, or both. We study properties of the upper domatic number of a graph, determine bounds on $D\left(G\right)$, and compare $D\left(G\right)$ to a related parameter, the transitivity $Tr\left(G\right)$ of $G$.

Keywords:

• Domination
• Domatic number
• Upper domatic number
• Transitivity

1 Introduction

Partitioning the vertex set of a graph into subsets with a specified property is a popular subject in graph theory. Arguably the most famous problem of graph partitioning is graph coloring, where the vertex set is partitioned into independent sets. The minimum order of such a partition is the well-studied chromatic number of a graph. Considering subsets that are dominating sets, Cockayne and Hedetniemi [1] in 1977 defined the domatic number to be the maximum order of a partition of the vertices of a graph into dominating sets.

More formally, a set $S\subseteq V\left(G\right)$ is a dominating set of a graph $G=(V,E)$ if every vertex in $V\left(G\right)-S$ is adjacent to a vertex in $S$. The domination number of $G$, denoted $\gamma \left(G\right)$, is the minimum cardinality of a dominating set of $G$. A dominating set with cardinality $\gamma \left(G\right)$ is a called a $\gamma$-set of $G$. Given two disjoint sets of vertices $R,S\subset V$, we say that $R$ dominates $S$, denoted $R\to S$, if every vertex in $S$ is adjacent to, or dominated by, at least one vertex in $R$. As previously mentioned, the domatic number of a graph $G$, denoted $d\left(G\right)$, is the maximum order $k$ of a vertex partition $\pi =\{V_1,V_2,\dots ,V_k\}$ such that for every $i$, $1\le i\le k$, $V_i$ is a dominating set of $G$. We call a partition $\pi$ into dominating sets a domatic partition and a domatic partition of order $d\left(G\right)$ is called a $d$-partition of $G$. Well over 100 papers have been published on this concept and its variations. The bibliography contains a sampling of these papers. For examples, cf. [2–9].

An equivalent definition of the domatic number is that it equals the maximum order $k$ of a vertex partition $\pi =\{V_1,V_2,\dots ,V_k\}$ such that for all $i,j$, $1\le i<j\le k$, $V_i\to V_j$ and $V_j\to V_i$. This definition of the domatic number suggests the following straightforward generalization. The upper domatic number, denoted $D\left(G\right)$, equals the maximum order $k$ of a vertex partition $\pi =\{V_1,V_2,\dots ,V_k\}$ such that for all $i,j$, $1\le i<j\le k$, either $V_i\to V_j$ or $V_j\to V_i$, or both. A vertex partition $\pi$ meeting this condition is called an upper domatic partition and an upper domatic partition of order $D\left(G\right)$ is called a $D$-partition of $G$.

In 2017, J. T. Hedetniemi and S. T. Hedetniemi [10] gave a different generalization of the domatic number as follows. The transitivity of a graph $Tr\left(G\right)$ is the maximum order $k$ of a vertex partition $\pi =\{V_1,V_2,\dots ,V_k\}$ such that for all $i,j$, $1\le i<j\le k$, $V_i\to V_j$. A vertex partition of $V$ meeting this condition is called a transitive partition and a transitive partition of $G$ having order $Tr\left(G\right)$ is called a $Tr$-partition of $G$.

By definition, therefore, every domatic partition is both a transitive partition and an upper domatic partition, while every transitive partition is an upper domatic partition. Thus, we have the following basic inequalities for any graph $G$.

Proposition 1

For any graph $G$ of order $n$, $1\le d\left(G\right)\le Tr\left(G\right)\le D\left(G\right)\le n$.

Our aim in this paper is to introduce and study the upper domatic number of a graph. We present properties and bounds on $D\left(G\right)$, and compare the upper domatic number and transitivity of graphs $G$.

1.1 Notation and terminology

In general, we follow the notation and terminology in [11]. Let $G=(V,E)$ be a graph. The open neighborhood of a vertex $v\in V$ is the set $N\left(v\right)=\left\{u\right|uv\in E\}$. Each vertex $u\in N\left(v\right)$ is called a neighbor of $v$, and $\left|N\left(v\right)\right|$ is called the degree of $v$, denoted $deg\left(v\right)$. The minimum and maximum degrees of vertices in a graph $G$ are denoted $\delta \left(G\right)$ and $\Delta \left(G\right)$, respectively. The closed neighborhood of a vertex $v\in V$ is the set $N\left[v\right]=N\left(v\right)\cup \left\{v\right\}$. The open neighborhood of a set $S\subseteq V$ of vertices is $N\left(S\right)={\bigcup }_{v\in S}N\left(v\right)$, while the closed neighborhood of a set $S$ is the set $N\left[S\right]={\bigcup }_{v\in S}N\left[v\right]$. Let $G\left[S\right]$ denote the subgraph induced by $S$ in $G$.

A cycle and path on $n$ vertices are denoted by $C_n$ and $P_n$, respectively. The complete graph on $n$ vertices is denoted by $K_n$, and its complement, the empty graph on $n$ vertices, is denoted ${\overline{K}}_n$. A clique is a maximal complete subgraph of $G$, and the clique number $\omega \left(G\right)$ is the maximum cardinality of a clique of $G$.

Let $\pi =\{V_1,V_2,\dots ,V_k\}$ be a vertex partition of a graph $G=(V,E)$. A subset $V_i$ with $\left|V_i\right|=1$ is called a singleton, and a subset $\left|V_i\right|\ge 2$ is called a non-singleton.

1.2 Domination digraphs

An equivalent definition of domatic partitions can be given using domination digraphs. Let $\pi =\{V_1,V_2,\dots ,V_k\}$ be a vertex partition of a graph $G=(V,E)$. From this partition one can construct a directed graph, or digraph, $DG\left(\pi \right)=(\pi ,E\left(\pi \right))$, the vertices of which correspond one-to-one with the sets $V_1,V_2,\dots ,V_k$ of $\pi$, with a directed arc $V_i\to V_j$ in $DG\left(\pi \right)$ if $V_i$ dominates $V_j$ in $G$, that is, $V_j\subseteq N\left(V_i\right)$. We call $DG\left(\pi \right)$ the domination digraph of $\pi$. Domination digraphs were introduced in 2012 by Goddard et al. [12]. A digraph $DG=(V,E)$ is called complete if for any two vertices $v_i,v_j\in V$, either $v_i\to v_j$ or $v_j\to v_i$, or both. A complete digraph is called bi-directed if for any two vertices $v_i$ and $v_j$, both $v_i\to v_j$ and $v_j\to v_i$. A complete digraph $DG=(V,E)$ is called a tournament if for any two vertices $v_i$ and $v_j$, either $v_i\to v_j$ or $v_j\to v_i$, but not both. A tournament $DG=(V,E)$ is called transitive if the vertices can be ordered $v_1,v_2,\dots ,v_n$ in such a way that for every $1\le i<j\le n$, $v_i\to v_j$ if and only if $i<j$. A (complete) digraph $DG$ of order $n$ is said to be transitive if it contains a transitive tournament of order $n$ as a sub-digraph, that is, $DG$ contains a spanning transitive tournament.

A set $V_i$ in a partition $\pi =\{V_1,V_2,\dots ,V_k\}$ is called a source set if the out-degree of vertex $V_i$ in its domination digraph $DG\left(\pi \right)$ is $k-1$. And the set $V_i$ is a sink set if the in-degree of vertex $V_i$ in $DG\left(\pi \right)$ is $k-1$. Note that if $\pi =\{V_1,V_2,\dots ,V_k\}$ is a transitive partition, then $V_1$ is a source set and $V_k$ is a sink set.

Using domination digraphs, we can give equivalent definitions of transitive, domatic, and upper domatic partitions. A vertex partition $\pi$ is transitive if its domination digraph is transitive, and is an upper domatic partition if its domination digraph is complete. The domatic number of a graph is the maximum integer $k$ such that $G$ has a vertex partition $\pi =\{V_1,V_2,\dots ,V_k\}$ whose domination digraph is a bi-directed complete graph.

2 The upper domatic number

2.1 Basic properties

We begin with some basic properties that will prove useful in the results that follow.

Proposition 2

If $\pi =\{V_1,V_2,\dots ,V_r\}$ is an upper domatic partition of a graph $G$, then the partition ${\pi }^{\prime }=\{V_1,V_2,\dots ,V_{i-1},V_i\cup V_j,V_{i+1},\dots ,V_{j-1},V_{j+1},\dots ,V_r\}$ obtained from $\pi$ by deleting $V_i$ and $V_j$ and adding to ${\pi }^{\prime }$ the union $V_i\cup V_j$, for any $1\le i<j\le r$, is also an upper domatic partition.

Proof

In the vertex partition ${\pi }^{\prime }$, we only need to show that for any $V_k$, $V_k\ne V_i\cup V_j$, either $V_k\to (V_i\cup V_j)$ or $(V_i\cup V_j)\to V_k$. There are essentially two cases: (i) $V_k\to V_i$ and $V_k\to V_j$, or (ii) either $V_i\to V_k$ or $V_j\to V_k$ or both. For (i), $V_k\to (V_i\cup V_j)$, and for any of the three possibilities of (ii), $(V_i\cup V_j)\to V_k$.

Corollary 3

If a graph $G$ has an upper domatic partition of order $k$, then it has an upper domatic partition of order $j$, for any $1\le j\le k$.

The following observations are straightforward.

Observation 4

Let $\pi =\{V_1,V_2,\dots ,V_k\}$be an upper domatic partition of a graph $G$.

1.	For each $V_i,V_j,i\ne j$, if $V_i\to V_j$, there are at least $\left|V_j\right|$ edges in $G$ between vertices in $V_i$ and $V_j$.
2.	For each $V_i,V_j,i\ne j$, there are at least $min\{\left|V_i\right|,\left|V_j\right|)$ edges in $G$ between vertices in $V_i$ and $V_j$.
3.	If vertices $v_1,v_2,\dots ,v_k$ are each in singleton sets in $\pi$, then the vertices $v_1,v_2,\dots ,v_k$ form a complete subgraph in $G$.
4.	If a vertex $u\in V_i$ is not adjacent to any vertex in $V_j$, then $V_i\to V_j$.
5.	If $u\in V_i$ with $deg\left(u\right)=x<k$, then $outdeg\left(V_i\right)\ge k-x-1$ in $DG\left(\pi \right)$. Further, if $V_i\to V_j$ and $u$ is adjacent to a vertex in $V_j$ for some $j$, then $outdeg\left(V_i\right)\ge k-x$ in $DG\left(\pi \right)$.

It was shown in [10] that the transitivity of any graph $G$ is at least as large as the transitivity of any subgraph of $G$.

Proposition 5

[10] If $H$ is any subgraph of a graph $G$, then $Tr\left(H\right)\le Tr\left(G\right)$.

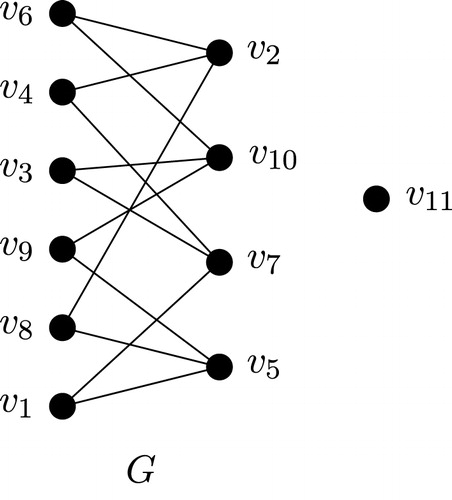
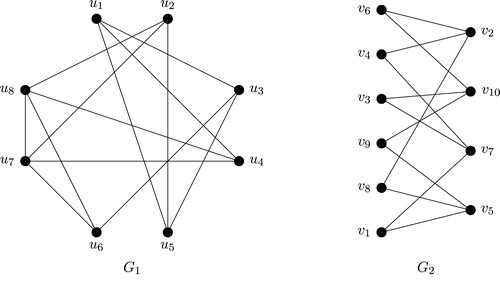
This is not necessarily true for the upper domatic number. To see this, consider the bipartite graph $G$ in Fig. 1. Let $H$ be the induced subgraph $G-v_{11}$, and note that $\pi =\{V_1=\{v_1,v_2,v_3\},V_2=\{v_4,v_5,v_6\},V_3=\{v_7,v_8,v_9\},V_4=\left\{v_{10}\right\}\}$ is an upper domatic partition of $H$ in which $V_1\to V_2\to V_3\to V_1$ and $V_4$ is a sink set. Thus, $D\left(H\right)\ge 4$, and it is straightforward to show that $D\left(H\right)=4$.

Fig. 1 $D\left(H\right)=4>D\left(G\right)=3$, where $H=G-v_{11}$.

The graph $G$, on the other hand, satisfies $D\left(G\right)<4$. This follows by observing that since $G$ has an isolated vertex $v_{11}$, any upper domatic partition of $G$ of order $4$, $\pi =\{V_1,V_2,V_3,V_4\}$, must have a source set $V_1$ containing vertex $v_{11}$. This means that the set $V_1-\left\{v_{11}\right\}$ is a dominating set of $H$. However, it can be seen that the domination number of $H$ is $3$, and that the vertices of any dominating set are incident to at least 8 of the 12 edges. Thus, one can check that there is no upper domatic partition of $G$ of order 4 containing such a source set.

The following relaxed form of Proposition 5, however, does hold for the upper domatic number.

Proposition 6

If $H$ is any subgraph of a graph $G$ and $H$ has a $D$-partition with a source set, then $D\left(H\right)\le D\left(G\right)$.

Proof

To get an upper domatic partition for $G$, use the $D$-partition for $H$ and add the vertices in $V\left(G\right)-V\left(H\right)$ to the source set in the $D$-partition for $H$.

Corollary 7

For any graph $G$, $D\left(G\right)\ge \omega \left(G\right)$.

We note that the bound of Corollary 7 is sharp for complete graphs $K_n$, for which $\omega \left(K_n\right)=n=D\left(K_n\right)$. On the other hand, the difference $D\left(G\right)-\omega \left(G\right)$ can be arbitrarily large; for complete bipartite graphs $K_{k,k}$, $\omega \left(K_{k,k}\right)=2<D\left(K_{k,k}\right)=k+1$. Note that an upper domatic partition of order $k+1$ can be formed by placing one vertex from each partite set into singleton sets and adding $k-1$ dominating sets containing one vertex from each partite set.

2.2 Small values of the upper domatic number

In this section we characterize the families of graphs $G$ having upper domatic number equal to $1$, $2$, or at least $3$. A star is a tree having at most one vertex of degree greater than one. A galaxy is a disjoint union of stars.

Theorem 8

For any graph $G$,

(1) $D\left(G\right)\ge 3$ if and only if $G$ contains either a $K_3$ or a $P_4$,

(2) $D\left(G\right)=2$ if and only if $G$ is a galaxy with at least one edge, and

(3) $D\left(G\right)=1$ if and only if $G={\overline{K}}_n$.

Proof

(1) Assume that $G$ contains a triangle or a $P_4$ subgraph. Each of these subgraphs has upper domatic number 3 and a $D$-partition with a source set. Thus, Proposition 6 implies that $D\left(G\right)\ge 3$.

Conversely, assume that $D\left(G\right)=k\ge 3$. Let $\pi =\{V_1,V_2,\dots ,V_k\}$ be an upper domatic partition of $G$. Consider only $V_1$, $V_2$, and $V_3$. Since $\pi$ is an upper domatic partition, it follows that either $V_i\to V_j$ or $V_j\to V_i$, or both, for every $1\le i<j\le 3$. From this we can assume either (i) the existence of a cyclic triple, where, without loss of generality, $V_1\to V_2$, $V_2\to V_3$ and $V_3\to V_1$, or (ii) the existence of a transitive triple, where $V_1\to V_2$, $V_1\to V_3$, and $V_2\to V_3$.

If (i) holds, let $v_1$ be an arbitrary vertex in $V_1$. Since $V_3\to V_1$, there must be a vertex $v_3\in V_3$, which is adjacent to $v_1$. Similarly, since $V_2\to V_3$, there must be a vertex $v_2\in V_2$ which is adjacent to vertex $v_3$. Finally, since $V_1\to V_2$, there must be a vertex $v_1^{\prime }\in V_1$ which is adjacent to $v_2$. If $v_1=v_1^{\prime }$, then $G$ has a triangle $\{v_1,v_2,v_3\}$, but if $v_1\ne v_1^{\prime }$, then $G$ has a $P_4$ subgraph $(v_1,v_3,v_2,v_1^{\prime })$.

If (ii) holds, let $v_3\in V_3$. Since $V_2\to V_3$, there must exist a vertex $v_2\in V_2$ which is adjacent to $v_3$. Since $V_1\to V_2$, there is a vertex $v_1\in V_1$ which is adjacent to $v_2$. Finally, since $V_1\to V_3$, there is a vertex $v_1^{\prime }\in V_1$, which is adjacent to $v_3$. If $v_1^{\prime }=v_1$, then $\{v_1,v_2,v_3\}$ forms a triangle in $G$, but if $v_1^{\prime }\ne v_1$, then $(v_1,v_2,v_3,v_1^{\prime })$ is a $P_4$ subgraph of $G$.

(2) Let $G=(V,E)$ be a galaxy with at least one edge, say $uv$. Then the partition defined by $\{V-\left\{u\right\},\left\{u\right\}\}$ is an upper domatic partition, and so $D\left(G\right)\ge 2$. But since $G$ is a galaxy, it does not contain a $K_3$ or a $P_4$. Hence, from (1) we know that $D\left(G\right)<3$. Thus, $D\left(G\right)=2$.

Conversely, assume that $D\left(G\right)=2$. Then by definition, $G$ has at least one edge. By (1) we know that $G$ has no triangle and no $P_4$ subgraph. Any trivial component of $G$ is the star $K_1$. Since $G$ has at least one edge, $G$ has at least one nontrivial component. Consider any nontrivial component $H$ of $G$ (if $G$ is connected $H=G$), and let $u$ be a vertex of $H$ having maximum degree $\Delta \left(H\right)$. Since $G$ has no triangles, $N\left(u\right)$ is an independent set. If $u$ has degree 1, then since $u$ has maximum degree, $H$ is the star $K_2$. Assume that $u$ has degree 2 or more. If a neighbor of $u$, say $v$, has a neighbor $z\notin N\left[u\right]$, then $(w,u,v,z)$, where $w\in N\left(u\right)$ and $w\ne v$ is a $P_4$ subgraph of $G$, a contradiction. Hence, every neighbor of $u$ has degree 1, so $H$ is a star, implying that $G$ is a galaxy.

(3) Trivially, $D\left({\overline{K}}_n\right)=1$. Assume that $D\left(G\right)=1$. If $G\ne {\overline{K}}_n$, then $G$ has at least one edge, say $uv$. Thus, the partition defined by $\{\left\{u\right\},V-\left\{u\right\}\}$ is an upper domatic partition, and so, $D\left(G\right)\ge 2$, a contradiction. Thus, $G={\overline{K}}_n$.

3 Bounds on the upper domatic number

For a set of vertices $S$, let $G-S$ be the graph formed from $G$ by removing the set $S$ from $G$.

Proposition 9

If $G$ is a graph with order $n$ and $S$ is a $\gamma$-set of $G$, then $$D\left(G\right)\ge D(G-S)+1.$$

Proof

Since $S$ along with the sets of a $D$-partition of $G-S$ is an upper domatic partition of $G$, $D\left(G\right)\ge D(G-S)+1$.

By Proposition 1, we have that $d\left(G\right)\le D\left(G\right)$. Proposition 9 suggests a way of improving this bound for graphs with a $d$-partition containing a set that is not independent.

Proposition 10

If $\pi =\{V_1,V_2,\dots ,V_k\}$ is a $d$-partition of $G$, with $G_i=G\left[V_i\right]$ for $1\le i\le k$, then $D\left(G\right)\ge d\left(G\right)-1+\max \{D\left(G_i\right):1\le i\le k\}$.

Proof

Let $\pi =\{V_1,V_2,\dots ,V_k\}$ be a $d$-partition of $G$, and let $G_i=G\left[V_i\right]$. Let $D\left(G_j\right)=\max \{D\left(G_i\right):1\le i\le k\}$ and let ${\pi }^{\prime }$ be a $D$-partition of $G_j$. We note that $(\pi -\left\{V_j\right\})\cup {\pi }^{\prime }$ is an upper domatic partition of $G$. Thus, $D\left(G\right)\ge d\left(G\right)-1+D\left(G\left[V_j\right]\right)$.

Corollary 11

If $G$ is a graph with $d\left(G\right)=D\left(G\right)$, then every $d$-partition of $G$ is a partition of the vertices of $G$ into independent dominating sets.

Proof

Let $\pi$ be a $d$-partition of $G$, and let $V_j$ be a set in $\pi$ that is not independent. Using the notation of Proposition 10, $D\left(G\right)\ge d\left(G\right)-1+D\left(G_j\right)$. Since $V_j$ is not an independent set, Theorem 8 implies that $D\left(G_j\right)\ge 2$. Thus, $D\left(G\right)\ge d\left(G\right)-1+D\left(G_j\right)\ge d\left(G\right)-1+2=d\left(G\right)+1$.

The following upper bound on the domatic number is well known.

Proposition 12

[1] For any graph $G$, $d\left(G\right)\le \delta \left(G\right)+1$.

This bound does not hold for $D\left(G\right)$. It is immediately obvious that for any complete graph $K_n$, the domatic number $d\left(K_n\right)=D\left(K_n\right)=n=\delta \left(G\right)+1$. Consider, however, the graph $G$ formed by adding a new vertex $u$ adjacent to exactly one vertex, say $v$, of a complete graph $K_n$. It is easy to see that $d\left(G\right)=2=\delta \left(G\right)+1$, while $D\left(G\right)=n$, since a set containing $\{u,v\}$ along with $n-1$ singleton sets, each containing a vertex of $K_n-\{u,v\}$, is a $D$-partition of $G$. Thus, for $n\ge 3$, $D\left(G\right)>2=\delta \left(G\right)+1$, and we see that a significant difference can exist between the domatic number and the upper domatic number. With this example, we have proved the following.

Proposition 13

For any positive integer $k$, there is a graph $G$ such that $D\left(G\right)-d\left(G\right)\ge k$, and such that $D\left(G\right)-(\delta \left(G\right)+1)\ge k.$

Although the bound involving minimum degree in Proposition 12 does not hold for the upper domatic number, we show that replacing minimum degree with maximum degree is an upper bound for $D\left(G\right)$.

Theorem 14

For any graph $G$, $D\left(G\right)\le \Delta \left(G\right)+1$.

Proof

Let $\pi =\{V_1,V_2,\dots ,V_{k+1}\}$ be a $D$-partition of $G$ ordered in such a way, that $\left|V_i\right|\ge \left|V_j\right|$ for $i<j$. We claim there is at least one vertex $v\in V_{k+1}$ with $deg\left(v\right)\ge k$. By Observation 4, it follows there must be at least $\left|V_{k+1}\right|$ edges between each of the sets $V_i$ and $V_{k+1}$, for $1\le i\le k$. Hence, the sum of the degrees of the vertices in $V_{k+1}$ is at least $k\left|V_{k+1}\right|$, and therefore, the average degree of the vertices in this set is at least $k$. Hence, $D\left(G\right)=k+1\le \Delta \left(G\right)+1$.

It is shown in [1] that $d\left(G\right)+d\left(\overline{G}\right)\le n+1$. Our Nordhaus–Gaddum type bounds for the upper domatic number follow from Theorem 14.

Corollary 15

Let $G$ be a graph of order $n$. Then $$D\left(G\right)+D\left(\overline{G}\right)\le n+\Delta \left(G\right)-\delta \left(G\right)+1.$$

Proof

Theorem 14 implies that $D\left(G\right)+D\left(\overline{G}\right)\le \Delta \left(G\right)+1+\Delta \left(\overline{G}\right)+1$. The result follows since $\Delta \left(\overline{G}\right)=n-\delta \left(G\right)-1$.

We note that the bound of Corollary 15 is obtained by the self-complementary graph $G=P_4$ for which $D\left(G\right)+D\left(\overline{G}\right)=3+3=4+2-1+1=n+\Delta \left(G\right)-\delta \left(G\right)+1$. It is also obtained the complete graph.

Corollary 16

If $G$ is a regular graph, then $D\left(G\right)+D\left(\overline{G}\right)\le n+1$.

An upper bound on the sum of the upper domatic number and the domination number of a graph also follows from Theorem 14. It is a well-known result (see 11]) that for graphs with order $n$, $\gamma \left(G\right)\le n-\Delta \left(G\right)$.

Corollary 17

If $G$ is a graph with order $n$, then $D\left(G\right)+\gamma \left(G\right)\le n+1.$

The following proposition was given in [10].

Proposition 18

[10] For any connected graph $G$ with $\delta \left(G\right)=3$, $Tr\left(G\right)\ge 4$.

Since $Tr\left(G\right)\le D\left(G\right)$, we have the following corollary.

Corollary 19

For any connected graph $G$ with $\delta \left(G\right)=3$, $D\left(G\right)\ge 4$.

Based on Corollary 19, one might think that for any graph $G$, $D\left(G\right)\ge \delta \left(G\right)+1$. However, this is not the case. The following examples show that $D\left(G\right)<\delta \left(G\right)$ is possible. Indeed, the difference $\delta \left(G\right)-D\left(G\right)$ can be arbitrarily large.

For integers $t\ge 2$ and $k\ge 2$, let $G_{t,k}$ be the complete multipartite graph with $t$ partite sets each having cardinality $k$. That is, $G_{t,k}=K_{\{k,k,\dots ,k\}}$ with $t$ partite sets.

Proposition 20

For the graph $G_{t,k}$ with $t$ even, $D\left(G_{t,k}\right)=\frac{kt+t}{2}$.

Proof

Let the partite sets be $U_1,U_2,\dots ,U_t$ and let $U_i=\{u_{i,1},u_{i,2},\dots ,u_{i,k}\}$ for $1\le i\le t$. Note that for any $1\le i<j\le t$, $\left\{u_i\right\}\to \left\{u_j\right\}$ and conversely, $\left\{u_j\right\}\to \left\{u_i\right\}$. Moreover, every two-element subset containing elements from different partite sets is a dominating set of $G_{t,k}$. That is, the partition $\pi =\{\left\{u_{1,1}\right\},\left\{u_{2,1}\right\},\dots ,\left\{u_{t,1}\right\},\{u_{1,2},u_{2,2}\},\{u_{3,2},u_{4,2}\},\dots ,$ $\{u_{t-1,2},u_{t,2}\},\dots ,\{u_{1,k},u_{2,k}\},\{u_{3,k},u_{4,k}\},\dots ,\{u_{t-1,k},v_{t,k}\}\}$ is an upper domatic partition. Thus, it follows that for this graph, $D\left(G\right)\ge t+\frac{(k-1)t}{2}=\frac{kt+t}{2}$.

To see that $D\left(G\right)\le \frac{kt+t}{2}$, observe that any upper domatic partition of order larger than $\frac{kt+t}{2}$ has at least $t+1$ singleton sets. But then at least two of these singleton sets are vertices in the same partite set and are not adjacent, contradicting Observation 4.

It follows from Proposition 20 that there exists a graph $G$ for which $D\left(G\right)=\delta \left(G\right)$, and there is a graph $G$ for which $D\left(G\right)<\delta \left(G\right)$. For examples, the graph $G_{4,2}$ has $D\left(G_{4,2}\right)=\delta \left(G_{4,2}\right)=6$, and the graph $G_{6,2}$ has $D\left(G_{6,2}\right)=9<\delta \left(G_{6,2}\right)=10$.

4 Upper domatic number versus transitivity

In this section, we first consider graphs $G$ having equal transitivity and upper domatic number. We then turn our attention to the differences in these two parameters.

By considering Theorem 8 together with the following two results proven in [10], we see that graphs $G$ satisfying $D\left(G\right)\le 3$ have equal upper domatic and transitivity numbers.

Theorem 21

[10] Let $G$ be a graph.

1.	$Tr\left(G\right)=1$ if and only if $G={\overline{K}}_n$.
2.	$Tr\left(G\right)=2$ if and only if $G$ is a galaxy with at least one edge.

Proposition 22

[10] For any graph $G$, $Tr\left(G\right)\ge 3$ if and only if $G$ contains either a triangle or a $P_4$ subgraph (not necessarily induced).

We now consider other examples of graph families having this property. Recall that $P_n$ and $C_n$ denote the path and cycle, of order $n$, respectively. The Cartesian product $G\square H$ of two graphs $G$ and $H$ is the graph with vertex set $V\left(G\right)\times V\left(H\right)$ and edges such that two vertices $(u,v)$ and $(w,x)$ are adjacent in $E(G\square H)$ if and only if either $u=w$ and $v$ is adjacent to $x$ in $H$, or $u$ is adjacent to $w$ in $G$ and $v=x$. The class of graphs called $n$-cubes is defined recursively as follows. The $0$-cube, denoted $Q_0$, is the graph $K_1$. The $n$-cube $Q_n$ is the graph $Q_n=Q_{n-1}\square P_2$.

Using the fact that $Tr\left(G\right)\le D\left(G\right)\le \Delta \left(G\right)+1$ (Theorem 14) and proofs similar to those in [13,10], we can easily prove the following.

Theorem 23

1.	For the path $P_n$, $n\ge 4$, $Tr\left(P_n\right)=D\left(P_n\right)=\Delta \left(P_n\right)+1=3$.
2.	For the cycle $C_n$, $n\ge 3$, $Tr\left(C_n\right)=D\left(C_n\right)=\Delta \left(C_n\right)+1=3$.
3.	For any cubic graph $G$, $Tr\left(G\right)=D\left(G\right)=\Delta \left(G\right)+1=4$.
4.	For $m,n\ge 4$, $Tr(P_m\square P_n)=D(P_m\square P_n)=\Delta (P_m\square P_n)+1=5$.
5.	For $m,n\ge 3$, $Tr(C_m\square C_n)=D(C_m\square C_n)=\Delta (C_m\square C_n)+1=5$.
6.	For any positive integer $n$, $Tr\left(Q_n\right)=D\left(Q_n\right)=\Delta \left(Q_n\right)+1=n+1$.

Theorem 23 gives several families of graphs having equal transitivity and upper domatic numbers. Acyclic graphs are another family with this property.

Theorem 24

If $G$ is acyclic, then $D\left(G\right)=Tr\left(G\right)$.

Proof

Let $G$ be any acyclic graph, and let $\pi =\{V_1,V_2,\dots ,V_k\}$ be an upper domatic partition of cardinality $k$ for $G$. We show that the sets in $\pi$ can be reordered $V_1^{\prime },V_2^{\prime },\dots ,V_k^{\prime }$, so that for $i<j$, $V_i^{\prime }$ dominates $V_j^{\prime }$. We first show that $\pi$ contains a source set. Let $T_r$ be a tree in $G$ rooted at $r$. We consider two cases:

Case (i). Let $r\in V_i$. For Case (i), if $c$ is a child of $r$, then either $c\in V_i$ or $V_i$ dominates the set of $\pi$ containing $c$. Thus, $V_i$ dominates all the sets of $\pi$ containing vertices in $N\left[r\right]$. Suppose there is some set $V_j\in \pi$ that is not dominated by $V_i$. Then no child of $r$ is in $V_j$, implying that $V_j$ does not dominate $V_i$, contradicting that $\pi$ is an upper domatic partition of $G$. Hence, $V_i$ is a source set in $\pi$, and we can let $V_1^{\prime }=V_i$.

Case (ii). If Case (i) does not hold, let $u$ be a vertex of maximum depth in $T_r$, such that parent($u$)’s set, say $V_i$, is different from the set $V_j$ containing $u$ and $V_i$ does not dominate $V_j$. Since Case (i) does not hold, at least one child of $r$ has this property, so the vertex $u$ exists. Moreover, since $\pi$ is an upper domatic partition, $V_j\to V_i$. Also note by the choice of $u$, if $u$ has a child, it is either in $V_j$ or $V_j$ dominates the child’s set. Again, if there is a set say $V_a$ such that $V_j$ does not dominate $V_a$, then $V_a$ has no vertex in $N\left(u\right)$. But then $V_j$ does not dominate $V_a$ and $V_a$ does not dominate $V_j$, contradicting that $\pi$ is an upper domatic partition. Thus, $V_j$ is a source set in $\pi$.

Therefore, there exists a source set in $\pi$. We let this set be the first set $V_1^{\prime }$ in a reordered $\pi$. We can create a new acyclic graph $G^{\prime }=G-V_1^{\prime }$. The partition ${\pi }^{\prime }=\pi -V_1^{\prime }$ will be an upper domatic partition for $G^{\prime }$. By repeating the above process, we can find the next set in the ordering of $\pi$, and after $k-1$ iterations the entire ordering.

We have seen several examples where the inequality $Tr\left(G\right)\le D\left(G\right)$ is tight. On the other hand, strict inequality is possible. For example, the graph $G_1$ in Fig. 2 has $4=Tr\left(G_1\right)<D\left(G_1\right)=5$. To see that $D\left(G_1\right)=5$, we note that $\{\{u_1,u_2\},\{u_3,u_4\},\{u_5,u_6\},\left\{u_7\right\},\left\{u_8\right\}\}$ is an upper domatic partition, so $D\left(G_1\right)\ge 5$, and Theorem 14 implies that $D\left(G_1\right)\le 5$. It can be verified by a straightforward, but detailed proof or by a computer search that $G_1$ is a graph with the fewest vertices having transitivity strictly less than its upper domatic number. Similarly, it can be proved that the bipartite graph $G_2$ in Fig. 2, for which $3=Tr\left(G_2\right)<D\left(G_2\right)=4$, is a graph with the fewest edges having this property. We note that Propositions 22 and 25 imply that $Tr\left(G_2\right)=3$. From Theorem 14, $D\left(G_2\right)\le 4$. The partition $\{\{v_1,v_2,v_3\},\{v_4,v_5,v_6\},\{v_7,v_8,v_9\},\left\{v_{10}\right\}\}$ is an upper domatic partition, and so, $D\left(G_2\right)=4$.

Fig. 2 $Tr\left(G_i\right)<D\left(G_i\right)$ for $i=\text{1, 2}$.

We next show that the difference between $D\left(G\right)$ and $Tr\left(G\right)$ can be made arbitrarily large. We will need the following result from [10].

Proposition 25

[10] If $G$ is a graph with $Tr\left(G\right)=k$, then there exist two adjacent vertices in $G$, each having degree $k-1$ or more.

Theorem 26

There exists a graph $G$ for which $D\left(G\right)-Tr\left(G\right)$ differ by at least $p$, for any positive integer $p$.

Proof

Let $n=2k+1$ for some positive integer $k>1$. We construct a bipartite graph $G$ with $n(k+1)$ vertices and $nk(k+1)$ edges as follows.

Let $V\left(G\right)=\{s_0,s_1,s_2,\dots ,s_{n-1}\}\cup \left\{x_{i,j}\right|0\le i\le n-1,1\le j\le k\}$. For $0\le i\le n-1$, let $X_i=\left\{x_{i,j}\right|1\le j\le k\}$ and $V_i=\left\{s_i\right\}\cup X_i$.

For $0\le i\le n-1$, add edges such that $s_i$ is adjacent to every vertex in $X_p$ where $p$ is the sum $i+j$ modulo $n$ for $1\le j\le k$. Finally, add the edges $s_i{x}_{a,b}$ such that $a+b\equiv i\left(modn\right)$. Now $G$ is a bipartite graph with partite sets $S=\left\{s_i\right|0\le i\le n-1\}$ and $X=\bigcup X_i$ for $1\le i\le n-1$, where each vertex in $X$ has degree $k+1$ and each vertex in $S$ has degree $k(k+1)$.

We note that the partition $\pi =\{V_0,V_1,\dots ,V_{n-1}\}$ is an upper domatic partition, so $D\left(G\right)\ge n=2k+1$. On the other hand, since every edge of $G$ is incident to a vertex in $X$ with degree $k+1$, Proposition 25 implies that $Tr\left(G\right)\le k+2$, and so, $D\left(G\right)-Tr\left(G\right)\ge k-1$.

5 Concluding remarks

We conclude by noting another difference in the transitivity number and the upper domatic number of a graph that leads us to making a conjecture. As we saw in Section 1.2, every transitive partition $\pi$ has at least one source set and at least one sink set. In fact, it was observed in [10] that a graph $G$ will always have a $Tr$-partition with at least two sink sets. Upper domatic partitions, on the other hand, do not necessarily behave similarly.

For example, consider the graph $G_2$ from Fig. 2. This graph has no $D$-partition with a source set. If $G_2$ had a $D$-partition with a source set $V_1$, then as in the proof of Proposition 29 , in the graph $G-V_1$, $\{V_2,V_3,V_4\}$ would be an upper domatic partition. But if $D(G-V_1)=3$, then $Tr(G-V_1)=3$ as well. This would imply that a transitive partition of $G$ of order four could be constructed, a contradiction. Additionally, the graph $G_2$ in Fig. 2 has no $D$-partition with two sink sets. To see this, note that the graph $G_2$ has $Tr\left(G\right)<D\left(G\right)=4$. Thus, if $G_2$ had a $D$-partition with two sink sets, then the partition would also be transitive, again a contradiction.

The question arises whether there are graphs with no $D$-partitions with a sink set. Unfortunately, we have neither found such a graph nor proven that one does not exist.

Conjecture 1

There exists a graph $G$ such that no $D$-partition of $G$ contains a sink set.

Our next results show that if Conjecture 1 is true for a graph $G$, then $D\left(G\right)\ge 5$.

Proposition 27

If $G$ has a $D$-partition $\pi$ of order $k$ that contains a set that is dominated by $k-2$ sets, then $G$ has a $D$-partition ${\pi }^{\prime }$ containing a sink set.

Proof

Let $\pi =\{V_1,V_2,\dots ,V_k\}$ be an upper domatic partition that contains a set $V_j$ that is dominated by $k-2$ sets. If $\pi$ does not have a sink set, consider the set $V_i$ that is dominated by $V_j$. Let $u$ be a vertex in $V_j$ that dominates a vertex in $V_i$. Let $X=V_i\cup V_j-\left\{u\right\}$. Then ${\pi }^{\prime }=\pi -\{V_i,V_j\}\cup \{X,\left\{u\right\}\}$ is a $D$-partition of $G$ with the sink set $\left\{u\right\}$ (cf. Proposition 2).

Corollary 28

If $D\left(G\right)\le 4$, then there exists a $D$-partition that contains a sink set.

Proof

It follows from previous results that if $D\left(G\right)\le 3$, then $Tr\left(G\right)=D\left(G\right)$, and there is a Tr-partition $\pi$ that is a $D$-partition. Thus, $\pi$ has a sink set. Hence, assume that $D\left(G\right)=4$. Let $\pi$ be a $D$-partition for $G$, and consider the domination digraph for $\pi$. There are four vertices and at least six arcs in this digraph, so some vertex must have in-degree at least $2=D\left(G\right)-2$. By Proposition 27, the result holds.

We also note that if Conjecture 1 holds, the following is true.

Proposition 29

If there exist graphs that have no D-partitions containing a sink set, then there exist graphs that have no D-partitions containing either a sink set or a source set.

Proof

Let $G$ be a graph for which $D\left(G\right)=k$, and $G$ has no $D$-partition containing a sink set. Assume that $k$ is the minimum integer for which a graph $G$ exists for which $D\left(G\right)=k$ and $G$ has no $D$-partitions containing a sink set. Let $\pi =\{V_1,V_2,\dots ,V_k\}$ be a $D$-partition of $G$, where, by assumption, $V_k$ is not a sink set, and assume that $V_1$ is a source set. This means that $V_1$ is a dominating set of $G$. Then ${\pi }^{\prime }=\{V_2,V_3,\dots ,V_k\}$ is an upper domatic partition of order $k-1$ of the graph $G^{\prime }=G-V_1$.

First, we claim that $D\left(G^{\prime }\right)=k-1$. From the upper domatic partition ${\pi }^{\prime }$, we know that $D\left(G^{\prime }\right)\ge k-1$. Suppose $D\left(G^{\prime }\right)>k-1$. Let $\{W_1,W_2,\dots ,W_r\}$ be a $D$-partition of $G^{\prime }$, where $r\ge k$. Then it follows that $\{V_1,W_1,W_2,\dots ,W_r\}$ is an upper domatic partition of $G$ of order greater than $k$; a contradiction. Thus, $D\left(G^{\prime }\right)=k-1$.

Now suppose that $G^{\prime }$ has a $D$-partition $\{U_1,U_2,\dots ,U_{k-1}\}$ in which $U_{k-1}$ is a sink. Then $\{V_1,U_1,U_2,\dots ,U_{k-1}\}$ is a $D$-partition of $G$ containing a sink; a contradiction.

Thus, $G^{\prime }$ has no $D$-partition containing a sink, but $D\left(G^{\prime }\right)=k-1<k$, which contradicts our assumption that $k$ is the minimum integer for which a graph $G$ exists having $D\left(G\right)=k$ and no $D$-partitions containing a sink set.

Thus, it follows that $G$ has no $D$-partitions containing either a sink set or a source set.