Certified domination

Abstract

Imagine that we are given a set $D$ of officials and a set $W$ of civils. For each civil $x\in W$, there must be an official $v\in D$ that can serve $x$, and whenever any such $v$ is serving $x$, there must also be another civil $w\in W$ that observes $v$, that is, $w$ may act as a kind of witness, to avoid any abuse from $v$. What is the minimum number of officials to guarantee such a service, assuming a given social network?

In this paper, we introduce the concept of certified domination that models the aforementioned problem. Specifically, a dominating set $D$ of a graph $G=(V_G,E_G)$ is said to be certified if every vertex in $D$ has either zero or at least two neighbours in $V_G\setminus D$. The cardinality of a minimum certified dominating set in $G$ is called the certified domination number of $G$. Herein, we present the exact values of the certified domination number for some classes of graphs as well as provide some upper bounds on this parameter for arbitrary graphs. We then characterise a wide class of graphs with equal domination and certified domination numbers and characterise graphs with large values of certified domination numbers. Next, we examine the effects on the certified domination number when the graph is modified by deleting/adding an edge or a vertex. We also provide Nordhaus–Gaddum type inequalities for the certified domination number.

Keywords:

• Certified domination
• Domination
• Corona
• Nordhaus–Gaddum

1 Introduction

Imagine that we are given a set $D$ of officials and a set $W$ of civils. For each civil $x\in W$, there must be an official $v\in D$ that can serve $x$, and whenever any such $v$ is serving $x$, there must also be another civil $w\in W$ that observes $v$, that is, $w$ may act as a kind of witness, to avoid any abuse from $v$. What is the minimum number of officials to guarantee such a service, assuming a given social network? This problem motivates us introducing the concept of certified domination. Specifically, let $D$ be a subset of the vertex set of a graph $G=(V_G,E_G)$. We say that $D$ dominates $G$ (or is a dominating set of $G$) if each vertex in the set $V_G\setminus D$ has a neighbour in $D$. The cardinality of a minimum dominating set in $G$ is called the domination number of $G$ and denoted by $\gamma \left(G\right)$, and any minimum dominating set of $G$ is called a $\gamma$-set. A dominating set $D$ of $G$ is called certified if every vertex $v\in D$ has either zero or at least two neighbours in $V_G\setminus D$. The cardinality of a minimum certified dominating set in $G$ is called the certified domination number of $G$ and denoted by ${\gamma }_{\mathrm{cer}}\left(G\right)$. A minimum certified dominating set of $G$ is called a ${\gamma }_{\mathrm{cer}}$-set. Notice that, by the definition, $V_G$ is a certified dominating set of $G$, and certainly $1\le {\gamma }_{\mathrm{cer}}\left(G\right)\le \left|V_G\right|$. Furthermore, one can observe that ${\gamma }_{\mathrm{cer}}\left(G\right)\ne \left|V_G\right|-1$.

There is a wealth of literature about domination and its variations in graphs; we refer to the excellent books of Haynes, Hedetniemi, and Slater [1,2]. The domination concept we introduce perfectly fits into that area where, for a given graph $G$, domination parameters are defined by imposing additional constraints on a dominating set $D$ or its complement $V_G\setminus D$. This area includes, to mention but a few, multiple domination, distance domination, or global domination. In particular, the problem of certified domination is closely related to the problem of existence a $D{D}_2$-pair in a graph, introduced by Henning and Rall in [3]. Recall, a set $X\subseteq V_G$ of vertices is $2$-dominating in $G$ if every vertex in $V_G\setminus X$ has at least two neighbours in $X$. A $D{D}_2$-pair of $G$ is a pair $(D,D_2)$ of disjoint sets of vertices of $G$ such that $D$ is a dominating set of $G$ and $D_2$ is a $2$-dominating set of $G$; a graph that has a $D{D}_2$-pair is called a $D{D}_2$-graph. One can observe that if $G$ has a $D{D}_2$-pair $(D,D_2)$, then the set $D$ is a certified dominating set. However, there are graphs $G$ with ${\gamma }_{\mathrm{cer}}\left(G\right)<\left|D\right|$ for any $(D,D_2)$-pair in $G$ (if any), see Fig. 1 for an illustration.

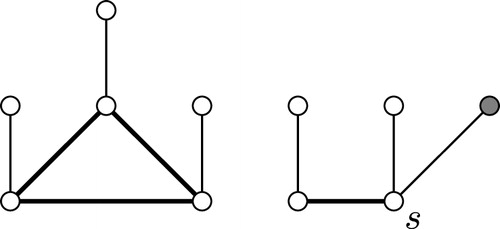
Fig. 1 The family of graphs $G_i$. (a) Black vertices form a certified dominating set $D_{\mathrm{c}}$ with $\left|D_{\mathrm{c}}\right|=i+3$, $i\ge 2$. (b) Black and grey vertices form a $(D,D_2)$-pair, respectively, with $\left|D\right|=2i+1$. Observe that if $i\ge 3$, then $G_i$ has no $(D,D_2)$-pair with $\left|D\right|\le i+3$.

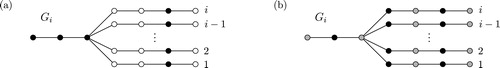
In Section 2, we present the exact values of the certified domination number for some elementary classes of graphs. Some upper bounds on this new parameter for an arbitrary graph are presented in Section 3. Then, in Sections 4 and 5, respectively, we characterise a wide class of graphs with equal domination and certified domination numbers and characterise graphs with large values of certified domination numbers. Next, in Section 6, we examine the effects on the certified domination number when the graph is modified by deleting/adding an edge or a vertex. Finally, Section 7 is devoted to Nordhaus–Gaddum type inequalities for the certified domination number.

1.1 Definitions and notation

For general graph theory terminology, we follow [4]. In particular, for a vertex $v$ of a graph $G=(V_G,E_G)$, its neighbourhood, denoted by $N_G\left(v\right)$, is the set of all vertices adjacent to $v$, and the cardinality of $N_G\left(v\right)$, denoted by ${deg}_G\left(v\right)$, is called the degree of $v$. The closed neighbourhood of $v$, denoted by $N_G\left[v\right]$, is the set $N_G\left(v\right)\cup \left\{v\right\}$. In general, for a subset $X\subseteq V_G$ of vertices, the neighbourhood of $X$, denoted by $N_G\left(X\right)$, is defined to be ${\bigcup }_{v\in X}{N}_G\left(v\right)$, and the closed neighbourhood of $X$, denoted by $N_G\left[X\right]$, is the set $N_G\left(X\right)\cup X$. The minimum (maximum, resp.) degree of a vertex in $G$ is denoted by $\delta \left(G\right)$ ($\Delta \left(G\right)$, resp.). A vertex of degree $\left|V_G\right|-1$ is called a universal vertex of $G$. A vertex of degree one is called a leaf, and the only neighbour of a leaf is called its support vertex (or simply, its support). If a support vertex has at least two leaves as neighbours, we call it a strong support, otherwise it is a weak support. The set of leaves of $G$ is denoted by $L_G$. For a leaf $v\in L_G$, its support vertex is denoted by $s_G\left(v\right)$, and for a weak support $v$, the unique leaf adjacent to $v$ is denoted by $l_G\left(v\right)$. The set of weak supports of $G$ is denoted by $S_1\left(G\right)$, while the set of strong supports of $G$ is denoted by $S_2\left(G\right)$.

2 Elementary graph classes

We begin by presenting the exact values of the certified domination number for some elementary classes of graphs.

Observation 2.1

If $P_n$ is an $n$-vertex path, then $${\gamma }_{\mathrm{cer}}\left(P_n\right)=\left\{\begin{array}{cc}\hfill 1\hfill & \text{if}n=1\text{or}n=3\text{;}\hfill \\ \hfill 2\hfill & \text{if}n=2\text{;}\hfill \\ \hfill 4\hfill & \text{if}n=4\text{;}\hfill \\ \hfill \lceil \frac{n}{3}\rceil \hfill & \text{otherwise.}\hfill \end{array}\right.$$

Observation 2.2

If $C_n$ is an $n$-vertex cycle, $n\ge 3$, then ${\gamma }_{\mathrm{cer}}\left(C_n\right)=\lceil \frac{n}{3}\rceil$.

Observation 2.3

If $K_n$ is an $n$-vertex complete graph, then $${\gamma }_{\mathrm{cer}}\left(K_n\right)=\left\{\begin{array}{cc}\hfill 1\hfill & \text{if}n=1\text{or}n\ge 3\text{;}\hfill \\ \hfill 2\hfill & \text{if}n=2\text{.}\hfill \end{array}\right.$$

Observation 2.4

If $K_{m,n}$ is a complete bipartite graph with $1\le m\le n$, then $${\gamma }_{\mathrm{cer}}\left(K_{m,n}\right)=\left\{\begin{array}{cc}\hfill 1\hfill & \text{if}m=1\text{and}n>1\text{;}\hfill \\ \hfill 2\hfill & \text{otherwise.}\hfill \end{array}\right.$$

Observation 2.5

If $W_n$ is an $n$-vertex wheel, then ${\gamma }_{\mathrm{cer}}\left(W_n\right)=1$.

In addition, we have the following two general observations on the certified domination number of a graph.

Observation 2.6

If $G$ is a graph of order at least three, then ${\gamma }_{\mathrm{cer}}\left(G\right)=1$ if and only if $G$ has a universal vertex.

Observation 2.7

If $G_1,\dots ,G_k$ are the connected components of a graph $G$, then ${\gamma }_{\mathrm{cer}}\left(G\right)={\sum }_{i=1}^k{\gamma }_{\mathrm{cer}}\left(G_i\right)$.

3 Upper bounds on the certified domination number

In this section we focus on upper bounds on the certified domination number. We start with two simple observations and then present our main result of this section: an upper bound on ${\gamma }_{\mathrm{cer}}\left(G\right)$ with respect to the domination number $\gamma \left(G\right)$ and the number $\left|S_1\left(G\right)\right|$ of weak supports in $G$.

Observation 3.1

Every support vertex of a graph $G$ belongs to every certified dominating set of $G$.

Proof

Let $D_c$ be a certified dominating set of $G$, let $s$ be a support vertex of $G$, and let $l$ be a leaf adjacent to $s$. If $s$ were not in $D_{\mathrm{c}}$, then $l$ should be in $D_{\mathrm{c}}$. But then $l$ would have only one neighbour in $V_G\setminus D_{\mathrm{c}}$, and $D_{\mathrm{c}}$ would not be a certified dominating set. □

Observation 3.2

Let $G$ be a graph of order $n$. If the strong supports of $G$ are adjacent to $k$ leaves in total, then ${\gamma }_{\mathrm{cer}}\left(G\right)\le n-k$. In particular, ${\gamma }_{\mathrm{cer}}\left(G\right)\le n-2\left|S_2\left(G\right)\right|$.

Proof

Let $L$ be the set of all leaf-neighbours of strong supports of $G$. Then $\left|L\right|=k$ and the set $V_G\setminus L$ is a certified dominating set of $G$. Thus ${\gamma }_{\mathrm{cer}}\left(G\right)\le |V_G\setminus L|=n-k\le n-2\left|S_2\left(G\right)\right|$ as $\left|L\right|\ge 2\left|S_2\left(G\right)\right|$. □

Before we present our main result, let us introduce some useful terminology. Let $D$ be a dominating set of a graph $G$. An element of $D$ that has all neighbours in $D$ is said to be shadowed with respect to $D$ (shadowed for short), an element of $D$ that has exactly one neighbour in $V_G\setminus D$ is said to be half-shadowed with respect to $D$ (half-shadowed for short), while an element of $D$ having at least two neighbours in $V_G\setminus D$ is said to be illuminated with respect to $D$ (illuminated for short). It is easy to observe that if $D$ is a minimum dominating set of a graph with no isolated vertices, then $D$ has no shadowed element, and if $D$ is a certified dominating set, then $D$ has no half-shadowed element.

Theorem 3.3

If $G$ is a connected graph, then ${\gamma }_{\mathrm{cer}}\left(G\right)\le \gamma \left(G\right)+\left|S_1\left(G\right)\right|$.

Proof

If $G$ is a graph of order at most two, then the inequality is obvious. Thus assume that $G$ has at least three vertices. Let $D$ be a $\gamma$-set of $G$ that minimises the number of half-shadowed vertices and such that $D$ does not contain any leaf of $G$. (Notice that such $D$ always exists as $G$ is connected and $\left|V_G\right|\ge 3$.) Let $D_{\mathrm{hs}}\subseteq D$ be the set of all half-shadowed vertices of $D$. If $D_{\mathrm{hs}}=0̸$, then ${\gamma }_{\mathrm{cer}}\left(G\right)=\gamma \left(G\right)\le \gamma \left(G\right)+\left|S_1\left(G\right)\right|$. Thus assume that $D_{\mathrm{hs}}\ne 0̸$.

Claim 1

If $v\in D_{\mathrm{hs}}$, then ${deg}_G\left(v\right)\ge 2$ and $v\notin S_2\left(G\right)$.

The inequality ${deg}_G\left(v\right)\ge 2$ follows from the choice of $D$, that is, from the assumption that $D\cap L_G=0̸$. To argue the second property, suppose on the contrary that $v$ is a strong support. Again, since $v$ has at least two neighbours in $L_G$ and $L_G\subseteq V_G-D$, $v$ would not be half-shadowed, a contradiction.

Next we show that all half-shadowed vertices are weak supports. Suppose on the contrary that there is a half-shadowed vertex $v\in D_{\mathrm{hs}}\setminus S_1\left(G\right)$ and let $u$ be the unique neighbour of $v$ in $V_G\setminus D$. Since $v$ is neither a weak nor strong support (by assumption and Claim 1, respectively), it implies that $u$ is not a leaf. Furthermore, we have the following claim.

Claim 2

The set $N_G\left(u\right)-\left\{v\right\}$ is a subset of $V_G-D$.

Otherwise the set $D\setminus \left\{v\right\}$ would be a smaller (than $D$) dominating set of $G$.

Finally, we have the following claim.

Claim 3

No vertex belonging to the set $N_G\left(v\right)\setminus \left\{u\right\}$ is shadowed.

If a vertex $w\in N_G\left(v\right)-\left\{u\right\}$ was shadowed, then the set $D\setminus \left\{w\right\}$ would be a smaller (than $D$) dominating set of $G$.

Consequently, keeping in mind the fact that none of neighbours of $v$ is a leaf (see Claim 1), and combining Claims 2 and 3, we conclude that the set $(D\setminus \left\{v\right\})\cup \left\{u\right\}$ would be a $\gamma$-set of $G$ with a smaller number of half-shadowed vertices, a contradiction. This proves that the set $D_{\mathrm{hs}}$ of half-shadowed vertices consists of weak supports of $G$ only.

Observe now that adding to $D$ all leaves adjacent to half-shadowed weak supports results in a dominating set $D^{\prime }$ of $G$ with no half-shadowed vertices, that is, $D^{\prime }$ is a certified dominating set of $G$. Therefore ${\gamma }_{\mathrm{cer}}\left(G\right)\le \left|D^{\prime }\right|=\left|D\right|+\left|D_{\mathrm{hs}}\right|=\gamma \left(G\right)+\left|D_{\mathrm{hs}}\right|\le \gamma \left(G\right)+\left|S_1\left(G\right)\right|$. □

From Observation 2.7 and Theorem 3.3, we immediately obtain the following corollary.

Corollary 3.4

If $G$ is a graph, then ${\gamma }_{\mathrm{cer}}\left(G\right)\le \gamma \left(G\right)+\left|S_1\left(G\right)\right|$.

4 Graphs with ${\gamma }_{\mathrm{cer}}=\gamma$

We continue our study on the certified domination number by focusing now on the class of graphs with ${\gamma }_{\mathrm{cer}}=\gamma$. When trying to characterise this class, one may expect that the main problem lies in leaves of a graph. In fact, from Corollary 3.4 we immediately have the first result.

Corollary 4.1

If $G$ is a graph with no weak support, then ${\gamma }_{\mathrm{cer}}\left(G\right)=\gamma \left(G\right)$.

The above corollary also follows from the next more general lemma.

Lemma 4.2

If a connected graph $G$ has at least three vertices, then ${\gamma }_{\mathrm{cer}}\left(G\right)=\gamma \left(G\right)$ if and only if there exists a minimum dominating set $D$ of $G$ such that $N_G\left(s\right)\setminus L_G⊈D$ for every $s\in S_1\left(G\right)$.

Proof

Assume first that ${\gamma }_{\mathrm{cer}}\left(G\right)=\gamma \left(G\right)$. Let $D_{\mathrm{c}}$ be a minimum certified dominating set of $G$. Then $D_{\mathrm{c}}$ is a minimum dominating set of $G$. Now, if $s\in S_1\left(G\right)$, then $D_{\mathrm{c}}\cap \{s,l_G\left(s\right)\}\ne 0̸$ (as $D_{\mathrm{c}}$ is dominating in $G$), $|D_{\mathrm{c}}\cap \{s,l_G\left(s\right)\}|\ne 2$ (otherwise $D_{\mathrm{c}}\setminus \left\{l_G\left(s\right)\right\}$ would be a smaller dominating set of $G$), and $D_{\mathrm{c}}\cap \{s,l_G\left(s\right)\}\ne \left\{l_G\left(s\right)\right\}$ (otherwise $l_G\left(s\right)$ would be half-shadowed). Thus $D_{\mathrm{c}}\cap \{s,l_G\left(s\right)\}=\left\{s\right\}$ and $(N_G\left(s\right)\setminus L_G)\cap (V_G\setminus D_{\mathrm{c}})=(N_G\left(s\right)\setminus \left\{l_G\left(s\right)\right\})\cap (V_G\setminus D_{\mathrm{c}})\ne 0̸$ (otherwise $s$ would be half-shadowed), and so $N_G\left(s\right)\setminus L_G⊈D_{\mathrm{c}}$.

Assume now that in $G$ there exists a $\gamma$-set $D$ such that $N_G\left(s\right)\setminus L_G⊈D$ for every $s\in S_1\left(G\right)$. Of all such sets, choose one, say $D^{\prime }$, that does not contain any leaf of $G$ (such $D^{\prime }$ exists in every connected graph of order at least three) and minimises the number of its half-shadowed vertices. We claim that such $D^{\prime }$ is a certified dominating set of $G$ (and therefore $\gamma \left(G\right)=\left|D^{\prime }\right|={\gamma }_{\mathrm{cer}}\left(G\right)$). Suppose, on the contrary, that some element $v$ of $D^{\prime }$ is half-shadowed. Let $v^{\prime }$ be the unique element of $N_G\left(v\right)\setminus D^{\prime }$. Since $v$ is half-shadowed, $v\notin S_2\left(G\right)$, and $v\notin S_1\left(G\right)$ (as every element of $S_1\left(G\right)$ is illuminated by the adjacent leaf and, by the assumption, by at least one non-leaf). Finally, since $D^{\prime }\cap L_G=0̸$ (by the choice of $D^{\prime }$) and $v\in D^{\prime }$, we have $v\notin L_G$ and $d_G\left(v\right)\ge 2$. Now, if it were $N_G\left(v^{\prime }\right)\cap (D^{\prime }\setminus \left\{v\right\})\ne 0̸$, then $D^{\prime }\setminus \left\{v\right\}$ would be a dominating set of $G$ smaller than $D^{\prime }$, a contradiction. Thus $N_G\left(v^{\prime }\right)\setminus \left\{v\right\}$ must be a nonempty subset of $V_G\setminus D^{\prime }$ and, then, $D^{\prime \prime }=(D^{\prime }\setminus \left\{v\right\})\cup \left\{v^{\prime }\right\}$ is a minimum dominating set of $G$ and it has less half-shadowed vertices than $D^{\prime }$, a final contradiction which proves that $\gamma \left(G\right)={\gamma }_{\mathrm{cer}}\left(G\right)$. □

Observe that if $G=\overline{K_n}$, then ${\gamma }_{\mathrm{cer}}\left(G\right)=n=\gamma \left(G\right)$. Next, if $G=l{K}_2$, then ${\gamma }_{\mathrm{cer}}\left(G\right)=2l\ne l=\gamma \left(G\right)$. In the latter case, $S_1\left(G\right)=V_G=L_G$ and $G$ has no minimum dominating set $D$ of $G$ such that $N_G\left(s\right)\setminus L_G⊈D$ for every $s\in S_1\left(G\right)$. Therefore, taking into account Observation 2.7 and Lemma 4.2, we obtain the following corollary for graphs which are not necessarily connected.

Corollary 4.3

If $G$ is a graph, then ${\gamma }_{\mathrm{cer}}\left(G\right)=\gamma \left(G\right)$ if and only if there exists a minimum dominating set $D$ in $G$ such that $N_G\left(s\right)\setminus L_G⊈D$ for every $s\in S_1\left(G\right)$.

Furthermore, we have the following relation between graphs each of which has a unique minimum dominating set and those for which ${\gamma }_{\mathrm{cer}}$ and $\gamma$ are equal.

Corollary 4.4

If a graph $G$ has a unique minimum dominating set, then ${\gamma }_{\mathrm{cer}}\left(G\right)=\gamma \left(G\right)$.

Proof

If $S_1\left(G\right)=0̸$, then ${\gamma }_{\mathrm{cer}}\left(G\right)=\gamma \left(G\right)$ by Corollary 4.1. Thus assume that $S_1\left(G\right)\ne 0̸$. Let $D$ be the minimum dominating set of $G$. From the uniqueness and minimality of $D$ it follows that $S_1\left(G\right)\subseteq D$ and $L_G\subseteq V_G\setminus D$. Now, if it were ${\gamma }_{\mathrm{cer}}\left(G\right)\ne \gamma \left(G\right)$, then, by Lemma 4.2, we could find $s\in S_1\left(G\right)$ such that $N_G\left(s\right)\setminus \left\{l_G\left(s\right)\right\}\subseteq D$, and then the set $(D\setminus \left\{s\right\})\cup \left\{l_G\left(s\right)\right\}$ would be another minimum dominating set of $G$, which is impossible. □

Remarks

From Corollary 4.1 and the fact that the problem of determining the domination number in bipartite planar subcubic graphs with no leaves is NP-hard (as it was observed in [5,6]), we immediately obtain the following: The problem of determining the certified domination number is NP-hard even in bipartite planar subcubic graphs with no leaves. Next, let $G$ be a graph with no isolated vertex. If $G$ has a minimal dominating set $D$ which is also a certified dominating set, then its complement $V_G\setminus D$ is a $2$-dominating set of $G$, and, therefore, $G$ is a $D{D}_2$-graph. Thus, from Corollaries 4.1 and 4.4, we have the following generalisation of Theorem 3 in [3]: Let $G$ be a graph with no isolated vertex. If $G$ has no weak support or $G$ has a unique dominating set, then $G$ is a $D{D}_2$-graph and it has a $(D,D_2)$-pair in which $\left|D\right|=\gamma \left(G\right)$.

5 Graphs with large values of ${\gamma }_{\mathrm{cer}}$

As we have already observed, for any graph $G$ of order $n$, ${\gamma }_{\mathrm{cer}}\left(G\right)\le n$, ${\gamma }_{\mathrm{cer}}\left(G\right)\ne n-1$, and there are graphs $G$ with ${\gamma }_{\mathrm{cer}}\left(G\right)=n$, for example, the complement of a complete graph $K_n$ or a 4-vertex path $P_4$. Thus it is natural to try to characterise all graphs with ${\gamma }_{\mathrm{cer}}=n$ and ${\gamma }_{\mathrm{cer}}=n-2$, respectively, which is carried out in this section. In particular, we prove that ${\gamma }_{\mathrm{cer}}\left(G\right)=n$ if and only if $G$ is the complement of a complete graph, the corona of a graph, or the union of both of them. Recall, the corona product (or simply, the corona) of two graphs $H$ and $F$ is the graph $G=H\circ F$ resulting from the disjoint union of $H$ and $\left|V_H\right|$ copies of $F$ in which the $i$th vertex of $H$ is joined to all vertices of the $i$th copy of $F$. If $F$ is a 1-vertex graph, $F=K_1$, then the corona $H\circ K_1$ is simply called the corona of $H$.

Lemma 5.1

Let $G$ be a connected graph of order $n$. If $G$ is the corona of some graph, then ${\gamma }_{\mathrm{cer}}\left(G\right)=n$.

Proof

Let $D_{\mathrm{c}}$ be a smallest certified dominating set of $G$. It suffices to prove that $D_{\mathrm{c}}=V_G$. This is obvious if $n=2$. Thus assume $n>2$. In this case, since $G$ is the corona of some graph, every vertex of $G$ either is a leaf of $G$ or is adjacent to exactly one leaf of $G$. From this and from Observation 3.1 it follows that $V_G\setminus L_G\subseteq D_{\mathrm{c}}$. Moreover, every leaf $l$ of $G$ also belongs to $D_{\mathrm{c}}$ (as otherwise its only neighbour $s_G\left(l\right)$ would be half-shadowed). Consequently, $L_G\subseteq V_G$ and therefore $D_{\mathrm{c}}=V_G$. □

Lemma 5.2

Let $G$ be a connected graph of order $n\ge 2$. If ${\gamma }_{\mathrm{cer}}\left(G\right)=n$, then $G$ is the corona of some graph.

Proof

The statement is obvious for connected graphs of order at most $4$. Thus assume that $G$ is a connected graph of order $n\ge 5$ and ${\gamma }_{\mathrm{cer}}\left(G\right)=n$. Now, since $\gamma \left(G\right)\le n∕2$ for every graph with no isolated vertex, so by Theorem 3.3 we have ${\gamma }_{\mathrm{cer}}\left(G\right)\le \gamma \left(G\right)+\left|S_1\left(G\right)\right|\le 2\gamma \left(G\right)\le n={\gamma }_{\mathrm{cer}}\left(G\right)$. Thus $\gamma \left(G\right)=n∕2$ and so $G$ is the corona of some graph (as it was proved in [7,8]). □

From the above lemmas, we immediately conclude with the following theorem.

Theorem 5.3

If $G$ is a graph of order $n$, then ${\gamma }_{\mathrm{cer}}\left(G\right)=n$ if and only if $G$ is either the complement of a complete graph, or the corona of a graph, or the union of both of them.

Remark

We incidentally observe that the above result implies the sharpness of the upper bound in the inequality ${\gamma }_{\mathrm{cer}}\left(G\right)\le \gamma \left(G\right)+\left|S_1\left(G\right)\right|$ (see Theorem 3.3 and Corollary 3.4) as well as in the inequality ${\gamma }_{\mathrm{cer}}\left(G\right)\le 2\gamma \left(G\right)$, since for the corona $G$ of any graph without an isolated vertex, we have $\left|S_1\left(G\right)\right|=\gamma \left(G\right)$ and ${\gamma }_{\mathrm{cer}}\left(G\right)=2\gamma \left(G\right)$.

5.1 Graphs with ${\gamma }_{\mathrm{cer}}=n-2$

A diadem graph of a graph $H$ is a graph obtained from the corona $H\circ K_1$ by adding a new vertex, say $v$, and joining $v$ to one of support vertices of $H\circ K_1$ (see Fig. 2).

Fig. 2 The diadem graph resulting from the corona $G=(K_3\cup K_2)\circ K_1$ by adding a leaf to the support vertex $s$ of $G$.

Lemma 5.4

If $G$ is a diadem graph of order $n$, then ${\gamma }_{\mathrm{cer}}\left(G\right)=n-2$.

Proof

Let $s$ be the unique strong support of $G$, and let $l_1,l_2$ be the two leaves of $G$ adjacent to $s$ in $G$. It is obvious that $V_G\setminus \{l_1,l_2\}$ is a certified dominating set of $G$. Let $D_{\mathrm{c}}$ be a smallest certified dominating set of $G$. Then $V_G\setminus L_G\subseteq D_{\mathrm{c}}$ (by Observation 3.1) and $\{l_1,l_2\}\cap D_{\mathrm{c}}=0̸$. Moreover, every leaf $l$ different from $l_1$ and $l_2$ belongs to $D_{\mathrm{c}}$ (otherwise $s_G\left(l\right)$ would be half-shadowed). Consequently $D_{\mathrm{c}}=V_G\setminus \{l_1,l_2\}$ and therefore ${\gamma }_{\mathrm{cer}}\left(G\right)=n-2$. □

Lemma 5.5

Let $G$ be a connected graph of order $n$. If ${\gamma }_{\mathrm{cer}}\left(G\right)=n-2$, then $G=C_3$, $G=C_4$, or $G$ is a diadem graph ( of a connected graph).

Proof

If $G$ is a connected graph of order at most $n\le 4$ and ${\gamma }_{\mathrm{cer}}\left(G\right)=n-2$, then $G=K_{1,2}$, $G=C_3$ or $G=C_4$. Thus assume that $n\ge 5$. In this case $\delta \left(G\right)=1$, as otherwise, since ${\gamma }_{\mathrm{cer}}\left(G\right)=\gamma \left(G\right)$ (by Corollary 4.1), ${\gamma }_{\mathrm{cer}}\left(G\right)=n-2$, and $\gamma \left(G\right)\le n∕2$, we would have $n-2={\gamma }_{\mathrm{cer}}\left(G\right)=\gamma \left(G\right)\le n∕2$, which is impossible. We now claim that $G$ is a diadem graph.

By way of contradiction, suppose that the claim is false. Let $G$ be a smallest counterexample, say of order $n$ ($n\ge 5$), such that ${\gamma }_{\mathrm{cer}}\left(G\right)=n-2$ and $G$ is not a diadem graph. Let $D_{\mathrm{c}}$ be a ${\gamma }_{\mathrm{cer}}$-set of $G$, and let $v$ and $u$ be the only elements of $V_G\setminus D_{\mathrm{c}}$. From the fact that $D_{\mathrm{c}}=V_G\setminus \{v,u\}$ is a certified dominating set of $G$ it follows that if $x\in D_{\mathrm{c}}$, then either $x\in N_G\left(v\right)\cap N_G\left(u\right)$ or $x\notin N_G\left(v\right)\cup N_G\left(u\right)$. This proves that $N_G\left(v\right)\cap D_{\mathrm{c}}=N_G\left(u\right)\cap D_{\mathrm{c}}$. In addition, the set $V_G\setminus N_G\left[\{v,u\}\right]$ is nonempty, as otherwise $\{v,u\}$ would be a certified dominating set of $G$ and we would have $n-2={\gamma }_{\mathrm{cer}}\left(G\right)\le \left|\{v,u\}\right|=2$, which is impossible.

Let $G^{\prime }$ denote the subgraph $G-N_G\left[\{v,u\}\right]$ of $G$. From the assumption ${\gamma }_{\mathrm{cer}}\left(G\right)=n-2$ it easily follows that ${\gamma }_{\mathrm{cer}}\left(G^{\prime }\right)=\left|V_{G^{\prime }}\right|$. Thus, by Theorem 5.3, every connected component of $G^{\prime }$ is an isolated vertex or the corona of a graph.

Let $H$ be a connected component of $G^{\prime }$. From the fact that $D_{\mathrm{c}}=V_G\setminus \{v,u\}$ is a minimum certified dominating set of $G$ it follows that at least one vertex of $H$ is not adjacent to any vertex belonging to $N_G\left[\{v,u\}\right]\setminus \{v,u\}$ as otherwise $D_{\mathrm{c}}\setminus V_H$ would be a certified dominating set of $G$, which is impossible as ${\gamma }_{\mathrm{cer}}\left(G\right)\le |D_{\mathrm{c}}\setminus V_H|<\left|D_{\mathrm{c}}\right|={\gamma }_{\mathrm{cer}}\left(G\right)$. From this we conclude that $G^{\prime }$ has no isolated vertex. Consequently, every connected component of $G^{\prime }$ is the corona of a graph.

We now claim that $K_2$ is not a connected component of $G^{\prime }$. Suppose on the contrary that $K_2$ on vertices $a$ and $b$ is a connected component of $G^{\prime }$. Then one of the vertices $a$ and $b$ is a leaf in $G$ and the latter one is adjacent to a vertex in $N_G\left[\{v,u\}\right]\setminus \{v,u\}$, say $a\in L_G$ and $b$ is adjacent to a vertex $w\in N_G\left[\{v,u\}\right]\setminus \{v,u\}$. Let $\tilde{G}$ denote the graph $G-\{a,b\}$ (of order $n-2$). For this graph either ${\gamma }_{\mathrm{cer}}\left(\tilde{G}\right)<n-4$, or ${\gamma }_{\mathrm{cer}}\left(\tilde{G}\right)=n-4$, or ${\gamma }_{\mathrm{cer}}\left(\tilde{G}\right)>n-4$. Assume first that ${\gamma }_{\mathrm{cer}}\left(\tilde{G}\right)<n-4$. Let ${\tilde{D}}_{\mathrm{c}}$ be a smallest certified dominating set of $\tilde{G}$. Then ${\tilde{D}}_{\mathrm{c}}\cup \left\{b\right\}$ (if $(N_G\left(b\right)\setminus \left\{a\right\})\setminus {\tilde{D}}_{\mathrm{c}}\ne 0̸$) or ${\tilde{D}}_{\mathrm{c}}\cup \{a,b\}$ (if $N_G\left(b\right)\setminus \left\{a\right\}\subseteq {\tilde{D}}_{\mathrm{c}}$) is a certified dominating set of $G$ and ${\gamma }_{\mathrm{cer}}\left(G\right)\le |{\tilde{D}}_{\mathrm{c}}\cup \{a,b\}|={\gamma }_{\mathrm{cer}}\left(\tilde{G}\right)+2<n-2$, a contradiction. Assume now that ${\gamma }_{\mathrm{cer}}\left(\tilde{G}\right)>n-4$. Then ${\gamma }_{\mathrm{cer}}\left(\tilde{G}\right)=n-2=\left|V_{\tilde{G}}\right|$ and, by Theorem 5.3, $\tilde{G}$ is the corona of a graph. But this is impossible as no vertex of $N_G\left[\{v,u\}\right]\setminus \{v,u\}$ is a leaf or a neighbour of exactly one leaf. Finally, assume that ${\gamma }_{\mathrm{cer}}\left(\tilde{G}\right)=n-4=\left|V_{\tilde{G}}\right|-2$. In this case the choice of $G$ implies that $\tilde{G}$ is the diadem graph in which $v$ and $u$ are leaves and $w$ is their only common neighbour. Now, it is obvious that the graph $G$ (obtained from $\tilde{G}$ by the addition of the vertices $a$ and $b$, and the edges $ab$ and $bw$) is a diadem graph, a contradiction.

Now, to complete the proof, it suffices to show that this smallest counterexample is not a counterexample, that is, it suffices to show that $G$ is a diadem graph. It is enough to prove that: (1) no vertex belonging to $N_G\left[\{v,u\}\right]$ is adjacent to a leaf of a connected component of $G^{\prime }$ of order at least four, (2) $v$ and $u$ have exactly one common neighbour, and (3) $v$ and $u$ are not adjacent in $G$.

(1)	Suppose on the contrary that there is a vertex in $N_G\left[\{v,u\}\right]$ adjacent to a leaf $l$ of a connected component $H$ (of order at least four) of $G^{\prime }$. Let $L$ be the set of leaves of $H$ within the distance at most $2$ from $s_H\left(l\right)$. Then $D=D_{\mathrm{c}}\setminus \left(L\cup \left\{s_H\left(l\right)\right\}\right)$ is a certified dominating set of $G$ and $\left|D\right|<\left|D_{\mathrm{c}}\right|$, a contradiction.
(2)	Suppose on the contrary that $|N_G\left[\{v,u\}\right]\setminus \{v,u\}|\ge 2$. Let us consider the set $S=\{x\in V_{G^{\prime }}:N_G\left(x\right)\cap N_G\left(\{v,u\}\right)\ne 0̸\}$. By (1), $S$ is a subset of $V_{G^{\prime }}\setminus L_{G^{\prime }}$. In addition, since $G^{\prime }$ is the corona of a graph, every vertex of $S$ is adjacent to a vertex of $L_{G^{\prime }}$. From the supposition $|N_G\left[\{v,u\}\right]\setminus \{v,u\}|\ge 2$ and from properties of elements of $S$ it follows that $D=\{v,u\}\cup (V_{G^{\prime }}\setminus L_{G^{\prime }})\cup (L_{G^{\prime }}\setminus N_{G^{\prime }}\left(S\right))$ ($=\{v,u\}\cup (V_{G^{\prime }}\setminus (N_G\left(S\right)\cap L_G))$) is a certified dominating set of $G$ and $\left|D\right|<\left|D_{\mathrm{c}}\right|$, a contradiction.
(3)	Suppose on the contrary that $vu\in E_G$, and consider the graph $G^{\prime \prime }=G-vu$ of order $n$, in which, by (2), $v$ and $u$ are leaves, and they have exactly one common neighbour, say $w$. In this graph we have either ${\gamma }_{\mathrm{cer}}\left(G^{\prime \prime }\right)>n-2$ (and therefore ${\gamma }_{\mathrm{cer}}\left(G^{\prime \prime }\right)=n$), or ${\gamma }_{\mathrm{cer}}\left(G^{\prime \prime }\right)=n-2$, or ${\gamma }_{\mathrm{cer}}\left(G^{\prime \prime }\right)<n-2$. Assume first that ${\gamma }_{\mathrm{cer}}\left(G^{\prime \prime }\right)=n$. Then, by Theorem 5.3, $G^{\prime \prime }$ is the corona of a graph, but this is impossible as leaves $v$ and $v$ share the same neighbour $w$. Assume now that ${\gamma }_{\mathrm{cer}}\left(G^{\prime \prime }\right)=n-2$. Then, by the choice of $G$, $G^{\prime \prime }$ is a diadem graph. Let $L$ be the set of leaves of $G^{\prime \prime }$ within the distance at most $3$ from $v$ (and $u$). Then $D=(D_{\mathrm{c}}\setminus (L\cup \left\{w\right\}))\cup \left\{v\right\}$ is a certified dominating set of $G$ and $\left|D\right|<\left|D_{\mathrm{c}}\right|$, a contradiction. Finally, assume that ${\gamma }_{\mathrm{cer}}\left(G^{\prime \prime }\right)<n-2$. Let $D_{\mathrm{c}}^{\prime \prime }$ be a smallest certified dominating of $G^{\prime \prime }$. Since $w$ is a strong support of $G^{\prime \prime }$, $w\in D_{\mathrm{c}}^{\prime \prime }$ by Observation 3.1, and $v,u\notin D_{\mathrm{c}}^{\prime \prime }$ by minimality of $D_{\mathrm{c}}^{\prime \prime }$. But then, $D_{\mathrm{c}}^{\prime \prime }$ is also a certified dominating set of $G$ and so ${\gamma }_{\mathrm{cer}}\left(G\right)<n-2$, a final contradiction. □

From Theorem 5.3, Lemmas 5.4 and 5.5, we have the final characterisation of graphs of order $n$ with ${\gamma }_{\mathrm{cer}}=n-2$.

Theorem 5.6

Let $G$ be a graph of order $n\ge 3$. Then ${\gamma }_{\mathrm{cer}}\left(G\right)=n-2$ if and only if $G$ is $C_3,C_4$, or a diadem graph, or $G$ is one of these three graphs with possible number of isolated vertices, or $G$ is the union of one of these three graphs with the corona of some graph, with possible number of isolated vertices. □

6 Influence of deleting/adding edge/vertex

In this section, following [9–12], to mention but a recent few, we examine the effects on the certified domination number when the graph is modified by deleting/adding an edge or a vertex. We observe that deleting an edge or a vertex may arbitrarily increase the certified domination number. For example, for the graph $G_i$ of order $2i+4$ illustrated in Fig. 3 (a) we have ${\gamma }_{\mathrm{cer}}\left(G_i\right)=i+1$ and ${\gamma }_{\mathrm{cer}}(G_i-e)=2i+4$. To argue a similar influence of deleting a vertex, consider a wheel graph $W_n$ with the hub $v$. We have ${\gamma }_{\mathrm{cer}}\left(W_n\right)=1$ and ${\gamma }_{\mathrm{cer}}(W_n-v)=\lceil (n-1)∕3\rceil$.

Fig. 3 Adding or deleting an edge may arbitrarily increase the certified domination number.

Adding an edge to a graph may also arbitrarily increase the certified domination number. Namely, consider the disconnected graph $H_i$ of order $2i+4$ illustrated in Fig. 3 (b). We have ${\gamma }_{\mathrm{cer}}\left(H_i\right)=i+2$ and ${\gamma }_{\mathrm{cer}}(H_i+e)=2i+4$. However, adding an edge to a connected graph does not increase the certified domination number, that is, ${\gamma }_{\mathrm{cer}}(G+e)\le {\gamma }_{\mathrm{cer}}\left(G\right)$ for any connected graph $G$. To argue this property, we use the following lemma.

Lemma 6.1

Let $D_{\mathrm{c}}$ be a ${\gamma }_{\mathrm{cer}}$-set of a connected graph $G$ of order $n\ge 2$. Then:

(a)	Every shadowed vertex in $D_{\mathrm{c}}$ is a weak support or a leaf.
(b)	Every non-leaf neighbour of a shadowed weak support is either an illuminated vertex or a shadowed weak support.

Proof

(a) Consider a shadowed vertex $v\in D_{\mathrm{c}}$. Suppose on the contrary that $v$ is neither a weak support nor a leaf in $G$. By minimality of $D_{\mathrm{c}}$, there are no shadowed strong supports in $D_{\mathrm{c}}$, in particular, $v$ is not a strong support, and thus all neighbours of $v$ are of degree at least two. Let $X\subseteq D_{\mathrm{c}}$ be a maximal subset of shadowed vertices such that (i) $v\in X$, (ii) the induced subgraph $G\left[X\right]$ is connected, and (iii) none of elements of $X$ is an illuminated vertex or a shadowed weak support. Next, for a vertex $x\in X$, define the set $B_G\left(x\right)=N_G\left(x\right)\setminus X$. Analogously, define the set $B_G\left(X\right)={\bigcup }_{x\in X}{B}_G\left(x\right)$.

Observe that by minimality of $D_{\mathrm{c}}$, each vertex $x\in X$ is a non-support vertex, and by the choice of $X$, and every element in $B_G\left(X\right)$ is either an illuminated vertex or a shadowed weak support.

Case $1$: $G\left[X\right]$ is a $1$-vertex graph. Let $L$ be the set of shadowed leaves within the distance $2$ from $v$. Then the set $D=D_{\mathrm{c}}\setminus \left(L\cup \left\{v\right\}\right)$ would be a certified dominating set of $G$ and $\left|D\right|<\left|D_{\mathrm{c}}\right|$, a contradiction.

Case $2$: $\left|X\right|\ge 2$ and ${\gamma }_{\mathrm{cer}}\left(G\left[X\right]\right)=\left|X\right|$. By Theorem 5.3, $G\left[X\right]$ is the corona of some connected graph. Observe that by the choice of $X$ and minimality of $D_{\mathrm{c}}$, if $x\in X$ is a leaf of $G\left[X\right]$, then the set $B_G\left(x\right)$ is non-empty.

Consider now a weak support $s$ in $G\left[X\right]$. Let $L_1$ be the set of leaves of $G\left[X\right]$ within the distance at most $2$ from $s$ and let $L_2$ be the set of shadowed leaves of $G$ within the distance $2$ from $L_1\cup \left\{s\right\}$. Then the set $D=D_{\mathrm{c}}\setminus (L_1\cup L_2\cup \left\{s\right\})$ is a certified dominating set of $G$ and $\left|D\right|<\left|D_{\mathrm{c}}\right|$, a contradiction.

Case $3$: $\left|X\right|\ge 3$ and ${\gamma }_{\mathrm{cer}}\left(G\left[X\right]\right)\le \left|X\right|-2$ (as the case ${\gamma }_{\mathrm{cer}}\left(G\left[X\right]\right)=\left|X\right|-1$ is impossible). Let $D_X$ be a ${\gamma }_{\mathrm{cer}}$-set of $G\left[X\right]$ and let ${\overline{D}}_X=X\setminus D_X$. Let $L_3$ be the set of shadowed leaves within the distance $2$ from ${\overline{D}}_X$. Then the set $D=D_{\mathrm{c}}\setminus ({\overline{D}}_X\cup L_3)$ is a certified dominating set of $G$ and $\left|D\right|<\left|D_{\mathrm{c}}\right|$, a contradiction.

(b) A non-leaf neighbour of a shadowed weak support $s\in D_{\mathrm{c}}$ is either illuminated or shadowed. If $s$ is shadowed, then, since it is not a leaf, it must be a weak support by (a). □

Theorem 6.2

If $G$ is a connected graph of order $n\ge 2$, then ${\gamma }_{\mathrm{cer}}(G+e)\le {\gamma }_{\mathrm{cer}}\left(G\right)$.

Proof

One can verify the validity of the theorem for graphs of order at most $n\le 4$. So assume $n\ge 5$ and let $D_{\mathrm{c}}$ be a ${\gamma }_{\mathrm{cer}}$-set of $G$.

Let $e=vw$, $v,w\in V_G$, be the added edge to $G$. If both $v,w\in D_{\mathrm{c}}$, then $D_{\mathrm{c}}$ is also a certified dominating set of the graph $G+e$. Similarly, if either both $v,w\notin D_{\mathrm{c}}$, or $v\notin D_{\mathrm{c}}$ and $w\in D_{\mathrm{c}}$ is illuminated, or $v\in D_{\mathrm{c}}$ is illuminated and $w\notin D_{\mathrm{c}}$, then $D_{\mathrm{c}}$ is a certified dominating set of $G+e$ as well. Therefore, in all aforementioned cases, we have ${\gamma }_{\mathrm{cer}}(G+e)\le \left|D\right|={\gamma }_{\mathrm{cer}}\left(G\right)$ as required.

Without loss of generality assume now that $v\notin D_{\mathrm{c}}$ and $w\in D_{\mathrm{c}}$ is shadowed (the case $w\notin D_{\mathrm{c}}$ and $v\in D_{\mathrm{c}}$ is shadowed can be analysed in a similar way). By Lemma 6.1 $\left(a\right)$, $w$ is either a weak support or a leaf of $G$.

Case $1$: $w$ is a weak support of $G$. Then the set $D=D_{\mathrm{c}}\setminus \left\{l_G\left(w\right)\right\}$ is a certified dominating set of $G+e$, and thus, ${\gamma }_{\mathrm{cer}}(G+e)\le \left|D\right|<\left|D_{\mathrm{c}}\right|={\gamma }_{\mathrm{cer}}\left(G\right)$.

Case $2$: $w$ is a leaf of $G$. By the choice of $D_{\mathrm{c}}$, it follows that the support vertex $s_G\left(w\right)$ is weak and shadowed. Therefore, by Lemma 6.1 $\left(b\right)$, every non-leaf neighbour of the weak support $s_G\left(w\right)$ in $G$ is either an illuminated vertex or a shadowed weak support of $G$. Let $L$ be the set of shadowed leaves within the distance $2$ from $s_G\left(w\right)$ in $G$. Then, the set $D=D_{\mathrm{c}}\setminus (L\cup \left\{s_G\left(w\right)\right\})$ is a certified dominating set in $G+e$, and hence ${\gamma }_{\mathrm{cer}}(G+e)\le \left|D\right|\le \left|D_{\mathrm{c}}\right|-1<{\gamma }_{\mathrm{cer}}\left(G\right)$. □

Adding a vertex can arbitrarily increase the certified domination number, which is not the case as in the model of classic domination. Indeed, for the graph $G_i$ of order $2i+1$ depicted in Fig. 4, we have ${\gamma }_{\mathrm{cer}}\left(G_i\right)=i$, while ${\gamma }_{\mathrm{cer}}(G_i+v)=2i+2$. However, bearing in mind Corollary 4.1, one can expect that the clue of the above construction lies in adding a leaf. Indeed, this is the case since one can prove that adding a non-leaf vertex does not effect the certified domination number significantly (the being added vertex $v$ is called a non-leaf vertex if $v$ is not a leaf in the resulting graph). Namely, we have the following theorem.

Fig. 4 Graph $G_i$ has $2i+1$ vertices, and ${\gamma }_{\mathrm{cer}}\left(G_i\right)=i$, while ${\gamma }_{\mathrm{cer}}(G_i+v)=2i+2$.

Theorem 6.3

If we add a non-leaf vertex $v$ to a graph $G$, then ${\gamma }_{\mathrm{cer}}(G+v)\le {\gamma }_{\mathrm{cer}}\left(G\right)+1$.

Proof

Let $D_{\mathrm{c}}$ be a ${\gamma }_{\mathrm{cer}}$-set of a graph $G$ and let $v$ be a new added vertex.

Case $1$: ${deg}_{G+v}\left(v\right)=2$. Let $u$ and $w$ be the two neighbours of $v$ in $G+v$. If either $u,w\notin D_{\mathrm{c}}$ or both $u,w\in D_{\mathrm{c}}$, then the set $D_{\mathrm{c}}\cup \left\{v\right\}$ is a certified dominating set of $G+v$, and thus ${\gamma }_{\mathrm{cer}}(G+v)\le {\gamma }_{\mathrm{cer}}\left(G\right)+1$. Otherwise, without loss of generality, we consider two subcases.

Subcase $1$.a: $u\notin D_{\mathrm{c}}$, $w\in D_{\mathrm{c}}$, and $w$ is illuminated. Then the set $D_{\mathrm{c}}$ remains a certified dominating set of $G+v$, and in this case, ${\gamma }_{\mathrm{cer}}(G+v)\le {\gamma }_{\mathrm{cer}}\left(G\right)$ holds.

Subcase $1$.b: $u\notin D_{\mathrm{c}}$, $w\in D_{\mathrm{c}}$, and $w$ is shadowed. If the vertex $w$ constitutes a $1$-vertex component of $G$, then the set $(D_{\mathrm{c}}\setminus \left\{w\right\})\cup \left\{v\right\}$ is a certified dominating set in $G+v$, thus getting ${\gamma }_{\mathrm{cer}}(G+v)\le {\gamma }_{\mathrm{cer}}\left(G\right)+1$. Otherwise, by Lemma 6.1 $\left(a\right)$, $w$ is either a weak support or a leaf of $G$. Now, similarly as in the proof of Theorem 6.2, we consider two subcases.

Subcase $1$.b.$1$: $w$ is a weak support of $G$. (We emphasise that this subcase includes the case when $w$ and the $l_G\left(w\right)$ constitute a $2$-vertex component of $G$.) Then the set $D_{\mathrm{c}}\setminus \left\{l_G\left(w\right)\right\}$ is a certified dominating set in $G+v$. In this case, ${\gamma }_{\mathrm{cer}}(G+v)\le {\gamma }_{\mathrm{cer}}\left(G\right)-1$ holds.

Subcase $1$.b.$2$: $w$ is a leaf of $G$, and $w$ together with the support vertex $s_G\left(w\right)$ does not constitute a $2$-vertex component of $G$. By the choice of $D_{\mathrm{c}}$, the support vertex $s_G\left(w\right)$ is weak and shadowed. By Lemma 6.1 $\left(b\right)$, every non-leaf neighbour of $s_G\left(w\right)$ in $G$ is either an illuminated vertex or a shadowed weak support of $G$. Again, let $L$ be the set of shadowed leaves within the distance $2$ from $s_G\left(w\right)$ in $G$. Then, the set $D=D_{\mathrm{c}}\setminus (L\cup \left\{s_G\left(w\right)\right\})$ is a certified dominating set in $G+v$. In this case, ${\gamma }_{\mathrm{cer}}(G+v)\le {\gamma }_{\mathrm{cer}}\left(G\right)-1$.

Case $2$: ${deg}_{G+v}\left(v\right)\ge 3$. Then, when adding $v$ to $G$, we first add only two edges, thus obtaining a temporary graph $G^{\prime }$, where ${deg}_{G^{\prime }}\left(v\right)=2$. Now, taking into account Case 1, we conclude that ${\gamma }_{\mathrm{cer}}\left(G^{\prime }\right)\le {\gamma }_{\mathrm{cer}}\left(G\right)+1$. Next, when adding all the remaining edges to $G^{\prime }$, sequentially, to obtain the final graph $G+v$, we apply Theorem 6.2, sequentially, for each of added edge, thus getting ${\gamma }_{\mathrm{cer}}(G+v)\le {\gamma }_{\mathrm{cer}}\left(G^{\prime }\right)\le {\gamma }_{\mathrm{cer}}\left(G\right)+1$ as required. □

7 Nordhaus–Gaddum type results

Following the precursory paper of Nordhaus and Gaddum [13], the literature has became abundant in inequalities of a similar type for many graph invariants, see a recent survey by Aouchiche and Hansen [14]. In particular, the following result is known for the domination number.

Theorem 7.1

[15–17] If $\overline{G}$ is the complement of a graph $G$ of order $n$, then:

(a)	$\gamma \left(G\right)\gamma \left(\overline{G}\right)\le n$;
(b)	$\gamma \left(G\right)+\gamma \left(\overline{G}\right)\le n+1$ with equality if and only if $G=K_n$ or $\overline{G}=K_n$.

Further sharpening of bounds was done for the case when, for example, both $G$ and $\overline{G}$ are connected [18] or for graphs with specified minimum degree [19], to mention but a few. In particular, the following theorem was proved in [20].

Theorem 7.2

[20] If $G$ is a graph of order $n$ and neither $G$ nor $\overline{G}$ has an isolated vertex, that is, $1\le \delta \left(G\right)\le n-2$, then $$\gamma \left(G\right)+\gamma \left(\overline{G}\right)\le ⌊\frac{n}{2}⌋+2.$$Moreover, if $n\ne 9$, the bound is attained if and only if $\{\gamma \left(G\right),\gamma \left(\overline{G}\right)\}=\{⌊n∕2⌋,2\}$.

In this section we provide some Nordhaus–Gaddumtype inequalities for the certified domination number. First, taking into account Corollary 4.1, Theorems 7.1 and 7.2, we obtain the following corollary.

Corollary 7.3

If $G$ is a graph of order $n$ and $min\{\delta \left(G\right),\delta \left(\overline{G}\right)\}\ge 2$, then $${\gamma }_{\mathrm{cer}}\left(G\right)+{\gamma }_{\mathrm{cer}}\left(\overline{G}\right)\le ⌊\frac{n}{2}⌋+2\text{and}{\gamma }_{\mathrm{cer}}\left(G\right){\gamma }_{\mathrm{cer}}\left(\overline{G}\right)\le n.$$

By enumerating all graphs of order at most $4$, we obtain the following observation.

Observation 7.4

Let $G$ be a graph of order $n$. Then:

(a)	${\gamma }_{\mathrm{cer}}\left(G\right)+{\gamma }_{\mathrm{cer}}\left(\overline{G}\right)={\gamma }_{\mathrm{cer}}\left(G\right){\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=4$ if $n=2$;
(b)	${\gamma }_{\mathrm{cer}}\left(G\right)+{\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=4$ and ${\gamma }_{\mathrm{cer}}\left(G\right){\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=3$ if $n=3$;
(c)	$\left({\gamma }_{\mathrm{cer}}\left(G\right)+{\gamma }_{\mathrm{cer}}\left(\overline{G}\right),{\gamma }_{\mathrm{cer}}\left(G\right){\gamma }_{\mathrm{cer}}\left(\overline{G}\right)\right)\in \{(3,2),(5,4),(6,6),(8,16)\}$ if $n=4$.

Next, we have the following theorem.

Theorem 7.5

If $G$ is a graph of order $n\ge 3$ and $min\{\delta \left(G\right),\delta \left(\overline{G}\right)\}=0$, then $${\gamma }_{\mathrm{cer}}\left(G\right)+{\gamma }_{\mathrm{cer}}\left(\overline{G}\right)\le n+1\text{and}{\gamma }_{\mathrm{cer}}\left(G\right){\gamma }_{\mathrm{cer}}\left(\overline{G}\right)\le n.$$In addition, if $min\{\delta \left(G\right),\delta \left(\overline{G}\right)\}=0$, then each of the above upper bounds is attainable, and the following statements are equivalent:

(a)	${\gamma }_{\mathrm{cer}}\left(G\right)+{\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=n+1$;
(b)	${\gamma }_{\mathrm{cer}}\left(G\right){\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=n$;
(c)	$G$ or $\overline{G}$ is the complement of $K_n$ or the union of the corona of some graph and a positive number of isolated vertices.

Proof

From the assumption $min\{\delta \left(G\right),\delta \left(\overline{G}\right)\}=0$, it follows that $max\{\Delta \left(\overline{G}\right),\Delta \left(G\right)\}=n-1$ and, therefore, ${\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=1$ or ${\gamma }_{\mathrm{cer}}\left(G\right)=1$. Now, since ${\gamma }_{\mathrm{cer}}\left(G\right)\le n$ and ${\gamma }_{\mathrm{cer}}\left(\overline{G}\right)\le n$, we get ${\gamma }_{\mathrm{cer}}\left(G\right)+{\gamma }_{\mathrm{cer}}\left(\overline{G}\right)\le n+1$ and ${\gamma }_{\mathrm{cer}}\left(G\right){\gamma }_{\mathrm{cer}}\left(\overline{G}\right)\le n$.

Assume now that $min\{\delta \left(G\right),\delta \left(\overline{G}\right)\}=0$, say $\delta \left(G\right)=0$. Then $\Delta \left(\overline{G}\right)=n-1$, and so ${\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=1$. Now, since ${\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=1$, it follows from each of the equalities ${\gamma }_{\mathrm{cer}}\left(G\right)+{\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=n+1$ and ${\gamma }_{\mathrm{cer}}\left(G\right){\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=n$ that ${\gamma }_{\mathrm{cer}}\left(G\right)=n$. Finally, since $\delta \left(G\right)=0$ and ${\gamma }_{\mathrm{cer}}\left(G\right)=n$, we conclude from Theorem 5.3 that $G$ is the complement of ${\overline{K}}_n$ or the union of the corona of some graph and a positive number of isolated vertices. This proves the implications $\left(a\right)\Rightarrow \left(c\right)$ and $\left(b\right)\Rightarrow \left(c\right)$. Opposite implications are straightforward. □

Finally, we have the following theorem.

Theorem 7.6

If $G$ is a graph of order $n\ge 5$, then $${\gamma }_{\mathrm{cer}}\left(G\right)+{\gamma }_{\mathrm{cer}}\left(\overline{G}\right)\le n+2\text{and}{\gamma }_{\mathrm{cer}}\left(G\right){\gamma }_{\mathrm{cer}}\left(\overline{G}\right)\le 2n.$$In addition, each of the above upper bounds is attainable, and the following statements are equivalent:

(a)	${\gamma }_{\mathrm{cer}}\left(G\right)+{\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=n+2$;
(b)	${\gamma }_{\mathrm{cer}}\left(G\right){\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=2n$;
(c)	$G$ or $\overline{G}$ is the corona of some graph.

Proof

If $min\{\delta \left(G\right),\delta \left(\overline{G}\right)\}\ge 2$, then ${\gamma }_{\mathrm{cer}}\left(G\right)+{\gamma }_{\mathrm{cer}}\left(\overline{G}\right)\le ⌊\frac{n}{2}⌋+2\le n+2$ and ${\gamma }_{\mathrm{cer}}\left(G\right){\gamma }_{\mathrm{cer}}\left(\overline{G}\right)$ $\le n\le 2n$ by Corollary 7.3. If $min\{\delta \left(G\right),\delta \left(\overline{G}\right)\}=0$, then ${\gamma }_{\mathrm{cer}}\left(G\right)+{\gamma }_{\mathrm{cer}}\left(\overline{G}\right)\le n+1\le n+2$ and ${\gamma }_{\mathrm{cer}}\left(G\right){\gamma }_{\mathrm{cer}}\left(\overline{G}\right)\le n\le 2n$ by Theorem 7.5.

Thus assume $min\{\delta \left(G\right),\delta \left(\overline{G}\right)\}=1$. Then $max\{\Delta \left(G\right),\Delta \left(\overline{G}\right)\}=n-2$. This also implies that ${\gamma }_{\mathrm{cer}}\left(G\right)>1$ and ${\gamma }_{\mathrm{cer}}\left(\overline{G}\right)>1$. Thus, since ${\gamma }_{\mathrm{cer}}\left(G\right)\le n$ and ${\gamma }_{\mathrm{cer}}\left(\overline{G}\right)\le n$, it suffices to show that ${\gamma }_{\mathrm{cer}}\left(G\right)=2$ or ${\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=2$. Without loss of generality assume that $\delta \left(G\right)=1$. Let $l$ be a leaf of $G$ and let $s$ be the only element of $N_G\left(l\right)$. We consider two cases: ${deg}_G\left(s\right)=n-2$, and ${deg}_G\left(s\right)\le n-3$.

Case 1: ${deg}_G\left(s\right)=n-2$. Let $t$ be the only element of $V_G\setminus N_G\left[s\right]$. Assume first that $d_G\left(t\right)\ge 2$. Let $u$ and $w$ be two neighbours of $t$ (and $s$). Now, because $N_G\left[\{s,t\}\right]=N_G\left[s\right]\cup N_G\left[t\right]=(V_G\setminus \left\{t\right\})\cup N_G\left[t\right]=V_G$, $\{u,w\}\subseteq N_G\left(s\right)\cap (V_G\setminus \{s,t\})$, $\{u,w\}\subseteq N_G\left(t\right)\cap (V_G\setminus \{s,t\})$, and ${\gamma }_{\mathrm{cer}}\left(G\right)>1$, we conclude that $\{s,t\}$ is a minimum certified dominating set of $G$, and ${\gamma }_{\mathrm{cer}}\left(G\right)=2$. Assume now that $d_G\left(t\right)=1$. In this case, let $u$ and $w$ be vertices such that $N_G\left(t\right)=\left\{u\right\}$ and $w\in N_G\left(s\right)\setminus \{l,u\}$. Since $N_{\overline{G}}\left[\{l,t\}\right]=N_{\overline{G}}\left[l\right]\cup N_{\overline{G}}\left[t\right]=(V_G\setminus \left\{s\right\})\cup (V_G\setminus \left\{u\right\})=V_G$, the set $\{l,t\}$ is dominating in $\overline{G}$. In addition, since $\{u,w\}\subseteq N_{\overline{G}}\left(l\right)\cap (V_G\setminus \{l,t\})$ and $\{s,w\}\subseteq N_{\overline{G}}\left(t\right)\cap (V_G\setminus \{l,t\})$, the set $\{l,t\}$ is certified dominating in $\overline{G}$. From this and from the fact that ${\gamma }_{\mathrm{cer}}\left(\overline{G}\right)>1$ it follows that ${\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=2$.

Case 2: ${deg}_G\left(s\right)\le n-3$. Let $t$ and $u$ be two elements of the set $V_G\setminus N_G\left[s\right]$. In this case, $\{l,s\}$ is a certified dominating set of $\overline{G}$, since $N_{\overline{G}}\left[\{l,s\}\right]=V_G$, $\{t,u\}\subseteq N_{\overline{G}}\left(l\right)\cap (V_G\setminus \{l,s\})$, and $\{t,u\}\subseteq N_{\overline{G}}\left(s\right)\cap (V_G\setminus \{l,s\})$. From this it again follows that ${\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=2$.

We now prove the equivalence of (a), (b), and (c). Let $G$ be a graph of order $n\ge 5$ such that ${\gamma }_{\mathrm{cer}}\left(G\right)+{\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=n+2$ (${\gamma }_{\mathrm{cer}}\left(G\right){\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=2n$, respectively). From this assumption, from Corollary 7.3 and Theorem 7.5 it follows that $min\{\delta \left(G\right),\delta \left(\overline{G}\right)\}=1$. Then, as we have already proved, ${\gamma }_{\mathrm{cer}}\left(G\right)=2$ or ${\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=2$, and therefore ${\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=n$ or ${\gamma }_{\mathrm{cer}}\left(G\right)=n$, respectively. From this and from Theorem 5.3 it follows that $\overline{G}$ or $G$ is the corona of some graph. Thus, we have proved the implications $\left(a\right)\Rightarrow \left(c\right)$ and $\left(b\right)\Rightarrow \left(c\right)$. Finally, assume that $G$ is the corona of some graph and $G$ is of order $n\ge 5$. Then ${\gamma }_{\mathrm{cer}}\left(G\right)=n$ by Theorem 5.3. From the fact that the corona has no isolated vertex, it follows that ${\gamma }_{\mathrm{cer}}\left(\overline{G}\right)>1$. Now, since $\delta \left(G\right)=1$, as in Case 2, we get ${\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=2$. Consequently, ${\gamma }_{\mathrm{cer}}\left(G\right)+{\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=n+2$ and ${\gamma }_{\mathrm{cer}}\left(G\right){\gamma }_{\mathrm{cer}}\left(\overline{G}\right)=2n$. This proves the implications $\left(c\right)\Rightarrow \left(a\right)$ and $\left(c\right)\Rightarrow \left(b\right)$. □

8 Concluding remarks

Since over the years researchers have published thousands of papers on the topic of domination in graphs, our paper cannot claim the right to cover the new model even partially, it should only be thought of as a very beginning, a small contribution to. In this section, we present three exemplary open problems that we find interesting and which research on we feel worth of being continued.

It is natural to characterise the class of critical graphs where the certified domination number increases on the removal of any edge/vertex as well as the class of stable graphs where the certified domination number remains unchanged on the removal of any edge/vertex. We point out that by Corollary 4.1, the class of critical (resp. stable) (with respect to the certified domination number) graphs with minimum degree $\delta \ge 3$ is the same as the class of critical (resp. stable) graphs with respect to domination number, see for example [21–23]. Therefore, we are left with characterising critical (resp. stable) graphs with minimum degree $\delta \le 2$. This is an open problem.

The problem of constructive characterisations of trees with equal domination parameters has received attention in the literature, see for example [24,3,25,26], to mention but a few recent. Following this concept, we leave as an open problem to provide a constructive characterisation of $(\gamma ,{\gamma }_{\mathrm{cer}})$-trees, that is, the class of trees with ${\gamma }_{\mathrm{cer}}=\gamma$.

Finally, let $G$ be a graph with no isolated vertex. Then no minimal dominating set of $G$ has a shadowed vertex. Consequently, if ${\gamma }_{\mathrm{cer}}\left(G\right)=\gamma \left(G\right)$, then none of ${\gamma }_{\mathrm{cer}}$-sets of $G$ has a shadowed vertex. (In particular, it follows from Corollary 4.1 that if $G$ has no weak support or $\delta \left(G\right)\ge 2$, then none of ${\gamma }_{\mathrm{cer}}$-sets of $G$ has a shadowed vertex.) A natural question then is whether the existence of a ${\gamma }_{\mathrm{cer}}$-set with no shadowed vertex implies the equality of the numbers ${\gamma }_{\mathrm{cer}}$ and $\gamma$. The answer to this question is not positive in general. 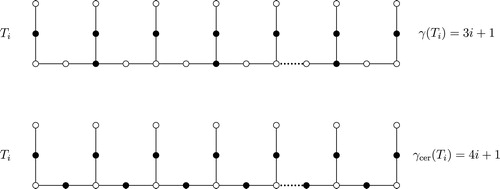For example, if $i$ is a positive integer and $T_i$ is the tree of order $8i+3$ obtained from the corona $P_{2i+1}\circ K_1$ by subdividing each of its edges exactly once, that is, $T_i=S(P_{2i+1}\circ K_1)$, then it is a routine exercise to check that $\gamma \left(T_i\right)=3i+1$, ${\gamma }_{\mathrm{cer}}\left(T_i\right)=4i+1$, and $T_i$ has a ${\gamma }_{\mathrm{cer}}$-set with no shadowed vertex, see Fig. 5 for an illustration. Therefore, we conclude our paper with the problem of characterising all graphs having a minimum certified dominating set with no shadowed vertex.

Fig. 5 Tree $T_i=S(P_{2i+1}\circ K_1)$ in which black vertices form a $\gamma$-set and a ${\gamma }_{\mathrm{cer}}$-set, respectively.

Acknowledgement

We would like to thank the referee for the remarkable comments and suggestions that improved the presentation of our results. R. Ziemann was supported by the grant BW 538-5300-B865-15.