Face antimagic labelings of toroidal and Klein bottle grid graphs

Abstract

In this paper we deal with the problem of labeling the vertices, edges and faces of a toroidal $T_n^m$ and Klein bottle $K_n^m$ grid graphs with $mn$ 4-sided faces by the consecutive integers from 1 up to $\left|V\left(T_n^m\right)\right|$ + $\left|E\left(T_n^m\right)\right|$ + $\left|F\left(T_n^m\right)\right|$ and $\left|V\left(K_n^m\right)\right|$ + $\left|E\left(K_n^m\right)\right|$ + $\left|F\left(K_n^m\right)\right|$ in such a way that the label of a 4-sided face and the labels of the vertices and edges surrounding that face all together add up to a weight of that face. These face-weights then form an arithmetic progression with common difference $d$. The paper examines the existence of such labelings for several differences $d$.

Keywords:

• Toroidal grid
• Klein bottle grid
• Super $d$-antimagic labeling

1 Introduction and definitions

Let $G\in \mathbf{G}$ be a family of $4$-regular graphs embedded on the surface of a torus or Klein bottle such that each of its face is $4$-sided. Let $V\left(G\right)$ , $E\left(G\right)$ and $F\left(G\right)$ be the vertex set, the edge set and the face set of a graph $G\in \mathbf{G}$, where $v$, $e$ and $f$ denote the cardinality of vertex, edge and face set respectively.

A labeling of type $(1,1,1)$ is a bijection $f:V\cup E\cup F\to \{1,2,\dots ,v+e+f\}.$ The weight of a $4$-sided face under a labeling of type $(1,1,1)$ is the sum of labels carried by that face and the edges and vertices surrounding it.

A labeling of type $(1,1,1)$ of graph $G\in \mathbf{G}$ is called $d$-antimagic if the set of weights of all $4$-sided faces is $W=\{a,a+d,a+2d,\dots ,a+(f-1)d\}$ for some integers $a>0$ and $d\ge 0$, where $f$ is the number of the $4$-sided faces.

The concept of the $d$-antimagic labeling of plane graphs was defined in [1]. The $d$-antimagic labeling of type $(1,1,1)$ for the generalized Petersen graph $P(n,2)$, hexagonal planar maps and grids can be found in [2,3] and [4], respectively. Lin et al. in [5] showed that prism $D_n$, $n\ge 3$, admits $d$-antimagic labeling of type $(1,1,1)$ for $d\in \{2,4,5,6\}$. The $d$-antimagic labeling of type $(1,1,1)$ for $D_n$ and for several $d\ge 7$ are described in [6].

In particular for $d=0$, Lih in [7] calls such labeling magic and describes magic ($0$-antimagic) labeling of type $(1,1,0)$ for wheels, friendship graphs and prisms. Kathiresan and Gokulakrishnan [8] provided the $0$-antimagic labeling of type $(1,1,1)$ for the families of planar graphs with $3$-sided faces, $5$-sided faces, $6$-sided faces and one external infinite face.

A $d$-antimagic labeling of type $(1,1,1)$ is called super if the smallest possible labels appear on the vertices. The super $d$-antimagic labelings of type $(1,1,1)$ for antiprisms and for $d\in \{0,1,2,3,4,5,6\}$ are described in [9] and for disjoint union of prisms and for $d\in \{0,1,2,3,4,5\}$ are given in [10]. The existence of a super $d$-antimagic labeling of type $(1,1,1)$ for the plane graphs containing a special Hamilton path is examined in [11] and a super $d$-antimagic labeling of type $(1,1,1)$ for disconnected plane graphs is given in [12]. For more details (see [13]). Plane graphs can also be embedded on other surfaces like torus, sphere, Klein bottle and projective plane (see [14]).

Motivated by the paper [15] we deal with the super $d$-antimagic labelings of type $(1,1,1)$ for the toroidal grid and we describe those labelings for several values of $d$.

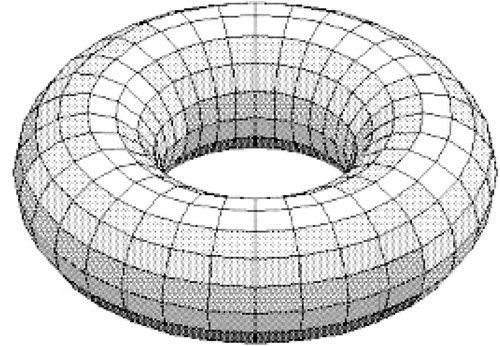
Let L be a regular square lattice and $P_n^m$ be an $m\times n$ quadrilateral section (with $n$ squares on the top and bottom sides and $m$ squares on the lateral sides,) cut from the regular square lattice L. First identify $2$ lateral sides of $P_n^m$ to form a cylinder, and finally identify the top and bottom sides of cylinder at their corresponding points; see Fig. 1.

Fig. 1 Toroidal grid graph.

Thus we get a toroidal grid graph $T_n^m$ with $mn$ $4$-sided faces, $mn$ vertices, and $2mn$ edges. More about toroidal grid can be found in ([16]).

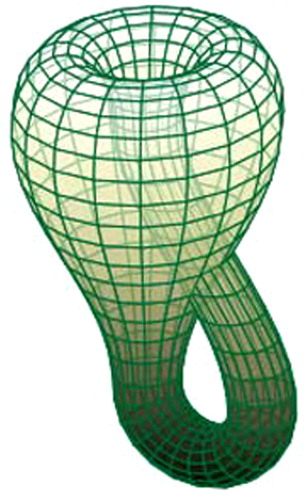
In the case of Klein bottle grid first we identify lateral side of $P_n^m$ to form a cylinder and then identify the top and bottom sides of the cylinder in opposite direction. By this identification of $P_n^m$, we get Klein bottle grid graph $K_n^m$ with $mn$ $4$-sided faces, $mn$ vertices, and $2mn$ edges. see Fig. 2.

Fig. 2 Klein bottle grid graph.

2 Necessary conditions

In this section, we shall find bound for a feasible value of $d$ for the super $d$-antimagic labeling of type $(1,1,1)$ for the toroidal grid $T_n^m$ and Klein bottle grid $K_n^m$.

Let $g$ be such a labeling. We consider weights of $4$-sided faces of the toroidal grid separately for a vertex labeling, an edge labeling and a face labeling. For $d$-antimagic vertex labeling ${\phi }_1:V\left(T_n^m\right)\to \{1,2,\dots ,\left|V\left(T_n^m\right)\right|\}$ the minimum possible weight of a $4$-sided face is at least $1+2+3+4$ and the maximum weight of a $4$-sided face is no more than $$\sum _{i=1}^4(\left|V\left(T_n^m\right)\right|-i+1)=4nm-6.$$Thus $$a_4+(f_4-1)d\le 4nm-6$$and $$d\le 4-\frac{12}{nm-1}.$$

Lemma 1

For every toroidal grid $T_n^m$, $n\ge 3$, $m\ge 3$, there is no $d$-antimagic vertex labeling with $d\ge 4$.

Assume that $T_n^m$ has a $d$-antimagic edge labeling ${\phi }_2$ with $\left|E\left(T_n^m\right)\right|$ values from the set $\{\left|V\left(T_n^m\right)\right|+1,\left|V\left(T_n^m\right)\right|+2,\dots ,\left|V\left(T_n^m\right)\right|+\left|E\left(T_n^m\right)\right|+\left|F\left(T_n^m\right)\right|\}$. Then the minimum possible weight of $4$-sided face is at least ${\sum }_{i=1}^4(\left|V\left(T_n^m\right)\right|+i)=4mn+10$ and the maximum weight of $4$-sided face is no more than $$\sum _{i=1}^4\left(\left|V\left(T_n^m\right)\right|+\left|E\left(T_n^m\right)\right|+\left|F\left(T_n^m\right)\right|+1-i\right)=16nm-6.$$Hence $$a_4+(f_4-1)d\le 16nm-6.$$It is easy to see that $$d\le 12-\frac{4}{nm-1}.$$

Lemma 2

For every toroidal grid $T_n^m$, $n\ge 3$, $m\ge 3$, there is no $d$-antimagic edge labeling with $d\ge 12$.

According to Lemma 1, Lemma 2 and the fact that under a $d$-antimagic face labeling ${\phi }_3$ with $f_4$ values from the set $\{\left|V\left(T_n^m\right)\right|+1,\left|V\left(T_n^m\right)\right|+2,\dots ,\left|V\left(T_n^m\right)\right|+\left|E\left(T_n^m\right)\right|+\left|F\left(T_n^m\right)\right|\}$ the parameter $d$ is no more than $3$, we obtain the following theorem.

Theorem 1

Let $T_n^m$, $n\ge 3$, $m\ge 3$, be a toroidal grid graph which admits $d_1$-antimagic vertex labeling ${\phi }_1$, $d_2$-antimagic edge labeling ${\phi }_2$ and $d_3$-antimagic face labeling ${\phi }_3$. If the labelings ${\phi }_1$, ${\phi }_2$ and ${\phi }_3$ combine to a super $d$-antimagic labeling of type $(1,1,1)$ then the parameter $d\le 17$.

Remark 1

Similarly, we can estimate the bound $d\le 17$ for the Klein bottle grid graph.

3 $d$-antimagic labeling of toroidal grid graph

Let $V\left(T_n^m\right)=\{(x_s,y_t):0\le s\le n-1,0\le t\le m-1\}$ be the vertex set of the graph $T_n^m$, $E\left(T_n^m\right)=\{(x_s,y_t)(x_{s+1},y_t):0\le s\le n-1,0\le t\le m-1\}\cup \{(x_s,y_t)(x_s,y_{t+1}):0\le s\le n-1,0\le t\le m-1\}$ be the edge set and $F\left(T_n^m\right)=\{z_{s,t}:0\le s\le n-1,0\le t\le m-1\}$ be the face set with indices $s$ and $t$ taken modulo $n$ and $m$ respectively. The face $z_{s,t}$ is bounded by edges $(x_s,y_t)(x_{s+1},y_t)$, $(x_{s+1},y_t)(x_{s+1},y_{t+1})$, $(x_s,y_{t+1})(x_{s+1},y_{t+1})$, $(x_s,y_t)(x_s,y_{t+1})$. (See Fig. 3).

Fig. 3 Toroidal grid identification.

In this section we will use a similar idea which was used for an investigation of $d$-antimagic labeling of generalized prism in [17].

Lemma 3

Let $T_n^m$ $n,m\ge 3$ be toroidal grid and let ${\alpha }_1\left((x_s,y_t)\right)=\{tn+1+s,0\le s\le n-1,0\le t\le m-1\}$and ${\alpha }_1\left((x_s,y_t)(x_{s+1},y_t)\right)=\{mn+(m-t)n-s,0\le s\le n-1,0\le t\le m-1\}$. If $n\ge 3$ and $m\ge 3$, then the partial weights of $z_{s,t}$ under the labeling ${\alpha }_1$ for every $t,0\le t\le m-2$, constitute an arithmetic sequence of difference $2$ and for $t=m-1$ the partial weights $z_{s,m-1}$ constitute the sequence $n(5m-1)+4,n(5m-1)+6,\dots ,n(5m+1)+2$.

Proof

Under the labeling ${\alpha }_1$, for every $t$, $0\le t\le m-1$, the partial weights of $4$-sided faces $z_{s,t}$ are as follows: $$w{t}_{{\alpha }_1}\left(z_{s,t}\right)={\alpha }_1\left((x_s,y_t)\right)+{\alpha }_1\left((x_{s+1},y_t)\right)+{\alpha }_1\left((x_s,y_{t+1})\right)+{\alpha }_1\left((x_{s+1},y_{t+1})\right)+{\alpha }_1\left((x_s,y_t)(x_{s+1},y_t)\right)+{\alpha }_1\left((x_s,y_{t+1})(x_{s+1},y_{t+1})\right)$$ (1) $$w{t}_{{\alpha }_1}\left(z_{s,t}\right)=\left\{\begin{array}{cc}n(4m+1+2t)+6+2s,\hfill & \mathrm{for}0\le s\le n-2,0\le t\le m-2\hfill \\ n(4m+1+2t)+4,\hfill & \mathrm{for}s=n-1,0\le t\le m-2\hfill \\ n(5m-1)+6+2s,\hfill & \mathrm{for}0\le s\le n-2,t=m-1\hfill \\ n(5m-1)+4,\hfill & \mathrm{for}s=n-1,t=m-1.\hfill \end{array}\right.$$(1) This shows that for every $t,s$, $0\le t\le m-1$, $0\le s\le n-1$, the partial weights of $z_{s,t}$ form the arithmetic sequence with difference 2 from $n(4m+1)+4$ up to $n(6m-1)+2$ and for every $s$, $0\le s\le n-1$, the partial weights of $z_{s,m-1}$ form the arithmetic sequence with difference 2 from $n(5m-1)+4$ up to $n(5m+1)+2$.

Lemma 4

Let $T_n^m$ $n,m\ge 3$ be toroidal grid and let for every $t$, $0\le t\le m-1$ $${\beta }_1\left((x_s,y_t)(x_s,y_{t+1})\right)=\left\{\begin{array}{cc}n(3m-t)-1-s,\hfill & \mathrm{for}0\le s\le n-2\hfill \\ n(3m-t),\hfill & \mathrm{for}s=n-1\hfill \end{array}\right.$$ $${\beta }_1\left(z_{s,t}\right)=\left\{\begin{array}{cc}n(3m+t)+3+s,\hfill & \mathrm{for}0\le s\le n-3\hfill \\ n(3m+t)+1,\hfill & \mathrm{for}s=n-2\hfill \\ n(3m+t)+2,\hfill & \mathrm{for}s=n-1.\hfill \end{array}\right.$$If $n\ge 3$ and $m\ge 3$, then under the labeling ${\beta }_1$ the partial weights of $z_{s,t}$, for every $t$, $0\le t\le m-1$, form an arithmetic sequence of difference $1$.

Proof

The partial weights of the $4$-sided faces $z_{s,t}$ under the labeling ${\beta }_1$, for every $t$, $0\le t\le m-1$, admit values $$w{t}_{{\beta }_1}\left(z_{s,t}\right)={\beta }_1\left((x_s,y_t)(x_s,y_{t+1})\right)+{\beta }_1\left(z_{s,t}\right)+{\beta }_1\left((x_{s+1},y_t)(x_{s+1},y_{t+1})\right)$$ (2) $$w{t}_{{\beta }_1}\left(z_{s,t}\right)=\left\{\begin{array}{cc}n(9m-t)-s,\hfill & \mathrm{for}0\le s\le n-2,0\le t\le m-1\hfill \\ n(9m-t)+1,\hfill & \mathrm{for}s=n-1,0\le t\le m-1.\hfill \end{array}\right.$$(2)

This shows that the partial weights of $z_{s,t}$ form the arithmetic sequence with difference 1 from $8mn+2$ up to $9mn+1$.

Lemma 5

Let for every $s$, $0\le s\le n-1$ $${\beta }_2\left((x_s,y_t)(x_s,y_{t+1})\right)=\left\{\begin{array}{cc}n(2m+t+1)+1+s,\hfill & \mathrm{for}0\le t\le m-2\hfill \\ 2mn+1+s,\hfill & \mathrm{for}t=m-1\hfill \end{array}\right.$$ $${\beta }_2\left(z_{s,t}\right)=n(4m-t)-s,\text{for}0\le t\le m-1.$$If $n\ge 3$ and $m\ge 3$, then the partial weights of $z_{s,t}$ under the labeling ${\beta }_2$, for every $t$, $0\le t\le m-1$ constitute an arithmetic sequence of difference $1$.

Proof

The partial weights of the $4$-sided faces $z_{s,t}$ under the labeling ${\beta }_2$, for every $t$, $0\le t\le m-1$, attain values

$w{t}_{{\beta }_2}\left(z_{s,t}\right)={\beta }_2\left((x_s,y_t)(x_s,y_{t+1})\right)+{\beta }_2\left(z_{s,t}\right)+{\beta }_2\left((x_{s+1},y_t)(x_{s+1},y_{t+1})\right)$ (3) $$w{t}_{{\beta }_2}\left(z_{s,t}\right)=\left\{\begin{array}{cc}n(8m+2+t)+3+s,\hfill & \mathrm{for}0\le s\le n-2,0\le t\le m-2\hfill \\ n(8m+2+t)+2,\hfill & \mathrm{for}s=n-1,0\le t\le m-2\hfill \\ n(7m+1)+3+s,\hfill & \mathrm{for}0\le s\le n-2,t=m-1\hfill \\ n(7m+1)+2,\hfill & \mathrm{for}s=n-1,t=m-1.\hfill \end{array}\right.$$(3) Thus, under the labeling ${\beta }_2$ the partial weights of $4$-sided faces $z_{s,k}$, $0\le s\le n-1$, $0\le t\le m-2$, constitute the arithmetic sequence of difference 1 from $n(8m+2)+2$ up to $n(9m+1)+1$ and for $0\le s\le n-1$ the partial weights $z_{s,m-1}$ attain consecutive values $n(7m+1)+2,n(7m+1)+3,\dots ,n(7m+2)+1$.

Theorem 2

For $n\ge 3$ and $m\ge 3$, the toroidal grid graph $T_n^m$ has a super $1$-antimagic labeling and a super $3$-antimagic labeling of type $(1,1,1)$.

Proof

Case d=1.

It follows from Lemmas 3 and 4 that under the labeling ${\alpha }_1$ and ${\beta }_1$ the weights of all $4$-sided faces are $$wt\left(z_{s,t}\right)=w{t}_{{\alpha }_1}\left(z_{s,t}\right)+w{t}_{{\beta }_1}\left(z_{s,t}\right)=\left\{\begin{array}{cc}n(13m+1+t)+6+s,\hfill & \mathrm{for}0\le s\le n-2,0\le t\le m-2\hfill \\ n(13m+1+t)+5,\hfill & \mathrm{for}s=n-1,0\le t\le m-2\hfill \\ 13mn+6+s,\hfill & \mathrm{for}0\le s\le n-2,t=m-1\hfill \\ 13mn+5,\hfill & \mathrm{for}s=n-1,t=m-1.\hfill \end{array}\right.$$This shows that the weights of the $4$-sided faces form an arithmetic sequence with difference 1 starts from $13mn+5$ up to $14mn+4$.

Case d=3.

Taking into account Lemmas 3 and 5 we can see that under the labeling ${\alpha }_1$ and ${\beta }_2$ the weights of $4$-sided faces are $$wt\left(z_{s,t}\right)=w{t}_{{\alpha }_1}\left(z_{s,t}\right)+w{t}_{{\beta }_2}\left(z_{s,t}\right)=\left\{\begin{array}{cc}n(12m+3+3t)+9+3s,\hfill & \mathrm{for}0\le s\le n-2,0\le t\le m-2\hfill \\ n(12m+3+3t)+6,\hfill & \mathrm{for}s=n-1,0\le t\le m-2\hfill \\ 12mn+9+3s,\hfill & \mathrm{for}0\le s\le n-2,t=m-1\hfill \\ 12mn+6,\hfill & \mathrm{for}s=n-1,t=m-1.\hfill \end{array}\right.$$Thus the weights of all $4$-sided faces constitute an arithmetic sequence of the difference $3$, namely $12mn+6$ up to $15mn+3$.

4 $d$-antimagic labeling of Klein bottle grid graph

Let $V\left(K_n^m\right)=\{(x_s,y_t):0\le s\le n-1,0\le t\le m-1\}$ be the vertex set, $E\left(K_n^m\right)=\{(x_s,y_t)(x_{s+1},y_t):0\le s\le n-1,0\le t\le m-1\}\cup \{(x_s,y_t)(x_s,y_{t+1}):0\le s\le n-1,0\le t\le m-2\}\cup \{(x_s,y_{m-1})(x_{n-s},y_0):0\le s\le n-1\}\cup \left\{(x_0,y_{m-1})(x_0,y_0)\right\}$ be the edge set and $F\left(K_n^m\right)=\{z_{s,t}:0\le s\le n-1,0\le t\le m-1\}$ be the face set. The face $z_{s,t}$ is bounded by edges $(x_s,y_t)(x_{s+1},y_t)$, $(x_{s+1},y_t)(x_{s+1},y_{t+1})$, $(x_s,y_{t+1})(x_{s+1},y_{t+1})$, $(x_s,y_t)(x_s,y_{t+1})$, for $0\le s\le n-1,0\le t\le m-2$ and $z_{s,m-1}$ is bounded by edges $(x_s,y_{m-1})(x_{s+1},y_{m-1})$, $(x_s,y_{m-1})(x_{n-s},y_0)$, $(x_{n-s},y_0)(x_{n-(s+1)},y_0)$, $(x_{s+1},y_{m-1})(x_{n-(s+1)},y_0)$ for $1\le s\le n-1$ and $z_{0,m-1}$ is bounded by edges $(x_0,y_{m-1})\left(x_1{y}_{m-1}\right)$, $(x_1,y_{m-1})\left(x_{n-1}{y}_0\right)$, $(x_0,y_0)\left(x_{n-1}{y}_0\right)$, $(x_0,y_{m-1})\left(x_0{y}_0\right)$, (see Fig. 4):

Fig. 4 Klein bottle grid identification.

Lemma 6

Let ${\lambda }_1\left((x_s,y_t)\right)=\{tn+1+s,0\le s\le n-1,0\le t\le m-1\}$and ${\lambda }_1\left((x_s,y_t)(x_{s+1},y_t)\right)=\{n(2m-t)-s,0\le s\le n-1,0\le t\le m-1\}$. If $n\ge 3$ and $m\ge 3$, then under the labeling ${\lambda }_1$ the partial weights of $z_{s,t}$ for every $t,s$, $0\le t\le m-2$, $0\le s\le n-1$, constitute an arithmetic sequence of difference $2$ and the partial weights of $z_{s,m-1}$ for $1\le s\le n-2$ are $5mn+5$ and for $z_{0,m-1}$ and $z_{n-1,m-1}$ are $n(5m-1)+5$.

Proof

Under the labeling ${\lambda }_1$, for every $t$, $0\le t\le m-2$, the partial weights of $4$-sided faces $z_{s,t}$ are as follows: $$w{t}_{{\lambda }_1}\left(z_{s,t}\right)={\lambda }_1\left((x_s,y_t)\right)+{\lambda }_1\left((x_{s+1},y_t)\right)+{\lambda }_1\left((x_s,y_{t+1})\right)+{\lambda }_1\left((x_{s+1},y_{t+1})\right)+{\lambda }_1\left((x_s,y_t)(x_{s+1},y_t)\right)+{\lambda }_1\left((x_s,y_{t+1})(x_{s+1},y_{t+1})\right)$$ (4) $$w{t}_{{\lambda }_1}\left(z_{s,t}\right)=\left\{\begin{array}{cc}n(4m+2t+1)+6+2s,\hfill & \mathrm{for}0\le s\le n-2,0\le t\le m-2\hfill \\ n(4m+2t+1)+4,\hfill & \mathrm{for}s=n-1,0\le t\le m-2.\hfill \end{array}\right.$$(4) This shows that for every $t$ and $s$, $0\le t\le m-2$, $0\le s\le n-1$, the partial weights of $4$-sided faces $z_{s,t}$ form the arithmetic sequence with difference 2 from $n(4m+1)+4$ up to $n(6m-1)+2$. For $1\le s\le n-2$ the partial weights of $z_{s,m-1}$ are $5mn+5$ and $w{t}_{{\lambda }_1}\left(z_{0,m-1}\right)=w{t}_{{\lambda }_1}\left(z_{n-1,m-1}\right)=n(5m-1)+5$.

Lemma 7

Let $${\mu }_1\left((x_s,y_t)(x_s,y_{t+1})\right)=\left\{\begin{array}{cc}n(3m-t)-s-1,\hfill & \mathrm{for}0\le s\le n-2,0\le t\le m-2\hfill \\ n(3m-t),\hfill & \mathrm{for}s=n-1,0\le t\le m-2\hfill \end{array}\right.$$

$${\mu }_1\left((x_s,y_{m-1})(x_{n-s},y_0)\right)=\left\{\begin{array}{cc}n(2m+1)-s-1,\hfill & \mathrm{for}0\le s\le n-2\hfill \\ n(2m+1),\hfill & \mathrm{for}s=n-1\hfill \end{array}\right.$$

$${\mu }_1\left(z_{s,t}\right)=\left\{\begin{array}{cc}n(3m+t)+3+s,\hfill & \mathrm{for}0\le s\le n-3,0\le t\le m-2\hfill \\ n(3m+t-1)+3+s,\hfill & \mathrm{for}n-2\le s\le n-1,0\le t\le m-2\hfill \end{array}\right.$$ $${\mu }_1\left(z_{s,m-1}\right)=\left\{\begin{array}{cc}n(4m-1)+3+s,\hfill & \mathrm{for}0\le s\le n-3\hfill \\ n(4m-2)+3+s,\hfill & \mathrm{for}n-2\le s\le n-1.\hfill \end{array}\right.$$If $n\ge 3$ and $m\ge 3$, then the partial weights of $z_{s,t}$ under the labeling ${\mu }_1$ for every $t$ and $s$, $0\le t\le m-1$, $0\le s\le n-1$, constitute an arithmetic sequence of difference $1$.

Proof

Under the given labeling ${\mu }_1$, for every $t$, $0\le t\le m-2$, the partial weights of the $4$-sided faces, admit the following values $$w{t}_{{\mu }_1}\left(z_{s,t}\right)={\mu }_1\left((x_s,y_t)(x_s,y_{t+1})\right)+{\mu }_1\left(z_{s,t}\right)+{\mu }_1\left((x_{s+1},y_t)(x_{s+1},y_{t+1})\right)$$ (5) $$w{t}_{{\mu }_1}\left(z_{s,t}\right)=\left\{\begin{array}{cc}n(9m-t)+1,\hfill & \mathrm{for}s=n-1,0\le t\le m-2\hfill \\ n(9m-t)-s,\hfill & \mathrm{for}0\le s\le n-2,0\le t\le m-2\hfill \end{array}\right.$$(5) (6) $$w{t}_{{\mu }_1}\left(z_{s,m-1}\right)=\left\{\begin{array}{cc}n(8m+1)+1,\hfill & \mathrm{for}s=n-1\hfill \\ n(8m+1)-s,\hfill & \mathrm{for}0\le s\le n-2.\hfill \end{array}\right.$$(6) This shows that the partial weights of $4$-sided faces form the arithmetic progression with difference 1 with values from $8mn+2$ up to $9mn+1$.

Lemma 8

Let ${\mu }_2\left((x_s,y_t)(x_s,y_{t+1})\right)=$ $$\begin{array}{cc}n(2m+t+1)+s+1,\hfill & \mathrm{for}0\le s\le n-1,0\le t\le m-2\hfill \end{array}$$ $${\mu }_2\left(z_{s,t}\right)=\begin{array}{cc}n(4m-t)-s,\hfill & \mathrm{for}0\le s\le n-1,0\le t\le m-2.\hfill \end{array}$$

If $n\ge 3$ and $m\ge 3$, then the partial weights of $z_{s,t}$ under the labeling ${\mu }_2$, for every $t$, $0\le t\le m-2$, constitute an arithmetic sequence of difference $1$.

Proof

Under the labeling ${\mu }_2$, for every $t$, $0\le t\le m-2$, the partial weights of the $4$-sided face attain values

$w{t}_{{\mu }_2}\left(z_{s,t}\right)={\mu }_2\left((x_s,y_t)(x_s,y_{t+1})\right)+{\mu }_2\left(z_{s,t}\right)+{\mu }_2\left((x_{s+1},y_t)(x_{s+1},y_{t+1})\right)$. (7) $$w{t}_{{\mu }_2}\left(z_{s,t}\right)=\left\{\begin{array}{cc}n(8m+2+t)+s+3,\hfill & \mathrm{for}0\le s\le n-2,0\le t\le m-2\hfill \\ n(8m+2+t)+2,\hfill & \mathrm{for}s=n-1,0\le t\le m-2.\hfill \end{array}\right.$$(7) Thus partial weights of $4$-sided faces under the labeling ${\mu }_2$, constitute the arithmetic sequence of difference 1.

Lemma 9

Let ${\mu }_2\left((x_s,y_{m-1})(x_{n-s},y_0)\right)=$ $$\left\{\begin{array}{cc}n(2m+1)-s+1,\hfill & \mathrm{for}1\le s\le n-1,t=m-1\hfill \\ 2mn+1,\hfill & \mathrm{for}s=0,t=m-1\hfill \end{array}\right.$$

$${\mu }_2\left(z_{s,m-1}\right)=\begin{array}{cc}n(3m+1)-s,\hfill & \mathrm{for}0\le s\le n-1.\hfill \end{array}$$If $n\ge 3$ and $m\ge 3$, then the partial weights of $z_{s,m-1}$ under the labeling ${\mu }_2$, constitute an arithmetic sequence of difference $1$.

Proof

Under the labeling ${\mu }_2$ defined for $0\le t\le m-2$ in Lemma 8 and for $t=m-1$ defined above, the partial weights of the $4$-sided face attain values $$w{t}_{{\mu }_2}\left(z_{s,m-1}\right)={\mu }_2\left((x_s,y_{m-1})(x_{n-s},y_0)\right)+{\mu }_2\left(z_{s,m-1}\right)+{\mu }_2\left((x_{s+1},y_{m-1})(x_{n-(s+1)},y_0)\right).$$ (8) $$w{t}_{{\mu }_2}\left(z_{s,m-1}\right)=\left\{\begin{array}{cc}n(7m-3s+3)+1,\hfill & \mathrm{for}1\le s\le n-1\hfill \\ n(7m+2)+1,\hfill & \mathrm{for}s=0.\hfill \end{array}\right.$$(8) Thus weights of $4$-sided faces under the labeling ${\mu }_2$, constitute the arithmetic sequence of difference 1.

Theorem 3

For $n\ge 3$ and $m\ge 3$, the Klein bottle grid graph $K_n^m$ admits a super $1$-antimagic labeling and a super $3$-antimagic labeling of type $(1,1,1)$.

Proof

Case d=1. It follows from Lemmas 6 and 7 that under the labeling ${\lambda }_1$ and ${\mu }_1$ the weights of all $4$-sided faces are $$wt\left(z_{s,t}\right)=w{t}_{{\lambda }_1}\left(z_{s,t}\right)+w{t}_{{\mu }_1}\left(z_{s,t}\right)=\left\{\begin{array}{cc}n(13m+t+1)+s+6,\hfill & \mathrm{for}0\le s\le n-2,0\le t\le m-2\hfill \\ n(13m+t+1)+5,\hfill & \mathrm{for}s=n-1,0\le t\le m-2\hfill \\ n(13m+1)+5-s,\hfill & \mathrm{for}1\le s\le n-1,t=m-1\hfill \\ 13mn+5,\hfill & \mathrm{for}s=0,t=m-1.\hfill \end{array}\right.$$This shows that the weights of the $4$-sided faces form an arithmetic sequence with difference 1 with values from $13mn+5$ up to $14mn+4$.

Case d=3.

Taking into account Lemmas 6, 8 and 9 along with the following swapping

•	${\lambda }_1\left((x_{n-3},y_{m-1})\right)⟷{\lambda }_1\left((x_{n-1},y_{m-1})\right)$
•	${\mu }_2\left(\left(z_{n-1,m-1}\right)\right)⟷{\mu }_2\left(\left(z_{n-3,m-1}\right)\right)$
•	${\mu }_2\left(\left(z_{n-2,m-1}\right)\right)⟷{\mu }_2\left(\left(z_{4,m-1}\right)\right)$
•	${\mu }_2\left(\left(z_{n-2,m-2}\right)\right)⟷{\mu }_2\left(\left(z_{4,m-2}\right)\right)$
•	${\mu }_2\left(\left(z_{n-1,m-2}\right)\right)⟷{\mu }_2\left(\left(z_{n-3,m-2}\right)\right)$

we can see that under the labeling ${\lambda }_1$ and ${\mu }_2$ the weights of $4$-sided faces are $$wt\left(z_{s,t}\right)=w{t}_{{\lambda }_1}\left(z_{s,t}\right)+w{t}_{{\mu }_2}\left(z_{s,t}\right)=\left\{\begin{array}{cc}n(12m+3t+3s+3)+9,\hfill & \mathrm{for}0\le s\le n-2,0\le t\le m-2\hfill \\ n(12m+3t+3)+6,\hfill & \mathrm{for}s=n-1,0\le t\le m-2\hfill \\ n(12m+3)-3s+6,\hfill & \mathrm{for}1\le s\le n-2,t=m-1\hfill \\ n(12m+1)+1,\hfill & \mathrm{for}s=0,t=m-1\hfill \\ n(12m+1)-2,\hfill & \mathrm{for}s=n-1,t=m-1.\hfill \end{array}\right.$$Finally the weights of the all $4$-sided faces of given graph form an arithmetic progression with the common difference $3$, starting from $12mn+6$ up to $15mn+3$.

5 Conclusion

In this paper we examine the existence of super $d$-antimagic labeling of type $(1,1,1)$ for toroidal grid graph $T_n^m$ and Klein bottle grid graph $K_n^m$. We show that $T_n^m$ and $K_n^m$ admit a super $d$-antimagic labeling of type $(1,1,1)$ for $d=\text{1,3}$, for all $n,m\ge 3$. However we tried to describe a super $d$-antimagic labeling of type $(1,1,1)$ of graphs $T_n^m$ and $K_n^m$ for $d=0,2,4$ but without success.

Therefore we conclude the paper with the following open problem.

Open problem 1

For the toroidal grid $T_n^m$ and Klein bottle grid ${\mathbb{K}}_n^m$, $n,m\ge 3$, determine whether there is a super $d$-antimagic labeling of type $(1,1,1)$ for $d=0,2,4$.

Acknowledgment

The research for this article was supported by APVV-15-0116 and by VEGA 1/0233/18.