Spanning trees with small diameters

Abstract

A spanning tree with small diameter of a graph has many applications. In this paper we first make the following conjecture and show that the condition is best possible if it is true. If a connected graph $G$ satisfies $\delta \left(G\right)\ge 3\left|G\right|∕(d+2)$, then $G$ has a spanning tree with diameter at most $d$, where $d\ge 4$ is an integer. We next prove that the conjecture holds if $d\ge 4$ is even or $d\in \{5,7,9\}$. Moreover, we prove that if $d\ge 5$ is odd and $\delta \left(G\right)\ge 3\left|G\right|∕(d+1)$, then $G$ has a spanning tree with diameter at most $d$.

Keywords:

• Spanning tree
• Diameter
• Minimum degree

1 Introduction

In this paper we consider finite simple graphs, which have neither loops nor multiple edges. Let $G$ be a connected graph with vertex set $V\left(G\right)$ and edge set $E\left(G\right)$. We denote by $\left|G\right|$ the order of $G$, that is, $\left|G\right|=\left|V\left(G\right)\right|$. For a vertex $v$ of $G$, we denote by ${deg}_G\left(v\right)$ the degree of $v$ in $G$ and by $N_G\left(v\right)$ the neighborhood of $v$. Thus ${deg}_G\left(v\right)=\left|N_G\left(v\right)\right|$. The minimum degree and the maximum degree of $G$ are denoted by $\delta \left(G\right)$ and $\Delta \left(G\right)$, respectively.

For two vertices $x$ and $y$ of $G$, $d_G(x,y)$ denotes the distance between $x$ and$y$, which is the minimum length of paths in $G$ connecting $x$ and $y$. The diameter $\mathrm{diam}\left(G\right)$ of $G$ is defined as $$\mathrm{diam}\left(G\right)=\underset{x,y\in V\left(G\right)}{max}{d}_G(x,y).$$On the other hand, the radius $\mathrm{radius}\left(G\right)$ of $G$ is defined as $$\mathrm{radius}\left(G\right)=\underset{v\in V\left(G\right)}{min}\left\{\underset{x\in V\left(G\right)}{max}{d}_G(v,x)\right\},$$where ${max}_{x\in V\left(G\right)}{d}_G(v,x)$ is called the eccentricity of $v$. Thus the radius of $G$ is the minimum value of eccentricities. A vertex whose eccentricity is equal to the $\mathrm{radius}\left(G\right)$ is called a central vertex of $G$, and the subgraph induced by central vertices is called the center of $G$. It is well-known that the center of a tree consists of one vertex or two adjacent vertices.

There are many research on spanning trees of graphs, for example, graph theoretical results can be found in Chapter 8 of [1] and [2], and algorithms for spanning trees can be found in [3] and [4]. In this paper, we consider graph theoretical results on spanning trees with small diameter of a given graph. Namely, for an integer $d\ge 4$, we give a minimum degree condition for a connected graph to have a spanning tree with diameter at most $d$. We first make a conjecture on such spanning trees.

Conjecture 1

Let $G$ be a connected graph and $d\ge 4$ be an integer. If (1) $$\delta \left(G\right)\ge \frac{3\left|G\right|}{d+2},$$(1) then $G$ has a spanning tree whose diameter is at most $d$. Moreover, if this statement holds, then the condition (1) is best possible.

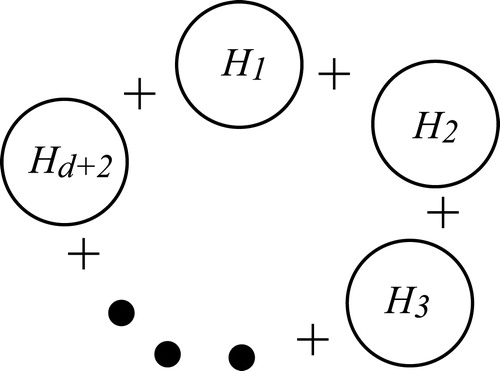
We now show that the condition (1) is sharp if the conjecture is true. Let $H_1,H_2,\dots ,H_{d+2}$ be $d+2$ disjoint copies of the complete graph of order $n$, and let $G$ be the graph obtained from $H_1,H_2,\dots ,H_{d+2}$ by joining every vertex of $H_i$ to every vertex of $H_{i+1}$ for all $1\le i\le d+2$, where $H_{d+3}=H_1$ (see Fig. 1). Then, $\left|G\right|=(d+2)n$ and $\delta \left(G\right)=3n-1=3\left|G\right|∕(d+2)-1$. Let $T$ be any spanning tree of $G$, and let $v$ be a center of $T$. Without loss of generality, we may assume that $v\in V\left(H_1\right)$. We first assume $d$ is odd. Let $t=(d+3)∕2$. Then for two vertices $x\in V\left(H_t\right)$ and $y\in V\left(H_{t+1}\right)$, $d_T(v,x)\ge d_G(v,x)\ge t-1$ and $d_T(v,y)\ge d_G(v,y)\ge t-1$. If the unique path $P_T(x,y)$ in $T$ connecting $x$ and $y$ passes through $v$, then $d_T(x,y)=d_T(x,v)+d_T(v,y)\ge 2(t-1)=d+1$. Hence the diameter of $T$ is at least $d+1$. If the path $P_T(x,y)$ does not pass through $v$, then by symmetry, we may assume that $d_T(v,y)\ge d_T(v,x)+1$, and thus $\mathrm{radius}\left(T\right)\ge d_T(v,y)\ge t$, which implies $\mathrm{diam}\left(T\right)\ge 2\cdot \mathrm{radius}\left(T\right)-1\ge d+2$ since $T$ is a tree. Therefore $G$ has no spanning tree with diameter at most $d$. In the case where $d$ is even, we can similarly show that $\mathrm{radius}\left(T\right)\ge (d+2)∕2$, and so $G$ has no spanning tree with diameter at most $d$. Consequently, the minimum degree condition (1) is best possible.

Fig. 1 A connected graph $G$ that has no spanning tree with diameter at most $d$ and satisfies $\delta \left(G\right)=3\left|G\right|∕(d+2)-1$, where every $H_i$ is a complete graph of order $n$.

In this paper, we prove the following two theorems, which verify that Conjecture 1 is true for even integers $d$ and for some odd integers $d$.

Theorem 2

Let $G$ be a connected graph, and $d\ge 4$ be an even integer. If $$\delta \left(G\right)\ge \frac{3\left|G\right|}{d+2},$$then $G$ has a spanning tree with diameter at most $d$.

Theorem 3

Let $G$ be a connected graph, and let $d\ge 5$ be an odd integer.

(1) If $d\in \{5,7,9\}$ and $$\delta \left(G\right)\ge \frac{3\left|G\right|}{d+2},$$then $G$ has a spanning tree with diameter at most $d$.

(2) If $$\delta \left(G\right)\ge \frac{3\left|G\right|}{d+1},$$then $G$ has a spanning tree with diameter at most $d$.

We now explain a relation of radius of a given graph and the minimum diameter of its spanning trees. It is well-known that the following lemma holds, and we use this fact in the proofs of theorems without mention.

Lemma 4

A connected graph $G$ with radius $r$ has a spanning tree with diameter at most $2r$.

Therefore, a research of the radius of a graph is closely related to one of its spanning tree with minimum diameter. We give some known results on the radius of a graph.

Theorem 5

Erdős, Pach, Pollack and Tuza, [5] Let $G$ be a connected graph with $\delta \left(G\right)\ge 2$. Then $$\mathrm{radius}\left(G\right)\le \frac{3}{2}\cdot \frac{\left|G\right|-3}{\delta \left(G\right)+1}+5.$$

This result was recently improved as follows.

Theorem 6

Kim, Rho, Song and Hwang [6] Let $G$ be a connected graph with $\delta \left(G\right)\ge 2$ and $\mathrm{radius}\left(G\right)\ge 3$. Then (2) $$\mathrm{radius}\left(G\right)\le \frac{3}{2}\cdot \frac{\left|G\right|}{\delta \left(G\right)+1}.$$(2)

Note that (2) of Theorem 6 directly implies that if $d\ge 6$ is even and $\delta \left(G\right)\ge (3\left|G\right|∕d)-1$, then $G$ has a spanning tree with diameter at most $d$ since $\delta \left(G\right)\ge (3\left|G\right|∕d)-1$ means $$\mathrm{radius}\left(G\right)\le \frac{3}{2}\cdot \frac{\left|G\right|}{\delta \left(G\right)+1}\le \frac{3}{2}\cdot \frac{\left|G\right|}{3\left|G\right|∕d}=\frac{d}{2}.$$

We conclude this section with remarks about spanning trees with diameter 2 or 3. It is clear that if a connected graph $G$ has a spanning tree $T$ with diameter 2, then $T$ has a vertex $v$ with ${deg}_T\left(v\right)=\left|G\right|-1$. Hence $G$ has a spanning tree with diameter 2 if and only if $G$ has a vertex of degree $\left|G\right|-1$.

We next show that there is no sufficient condition using $\delta \left(G\right)\ge c\left|G\right|$ with a constant number $0<c<1$ for a graph $G$ to have a spanning tree with diameter 3. Consider a graph $G$ with $\Delta \left(G\right)\le \left|G\right|-2$, which has no spanning tree with diameter 2. It is obvious that $G$ has a spanning tree with diameter 3 if and only if $G$ has an edge $uv$ such that $N_G\left(u\right)\cup N_G\left(v\right)=V\left(G\right)$. Namely, $G$ does not have a spanning tree with diameter 3 if and only if for every edge $xy$, there is a vertex $z$ such that $z\notin N_G\left(x\right)\cup N_G\left(y\right)$. In $\overline{G}$, the complement of $G$, this situation on $x,y,z$ is equivalent to $z\in N_{\overline{G}}\left(x\right)\cap N_{\overline{G}}\left(y\right)\ne 0̸$ for $xy⁄\in E\left(\overline{G}\right)$. So if $\mathrm{diam}\left(\overline{G}\right)=2$, then this situation holds in $\overline{G}$, and hence $G$ does not have a spanning tree with diameter 3.

In [7], Brown showed that there is a graph $H$ with $\left|H\right|=q^2+q+1$, $\Delta \left(H\right)=q+1$ and $\mathrm{diam}\left(H\right)=2$ for a prime power $q$. Then $\overline{H}$ does not have a spanning tree with diameter 3 by $H=\overline{\overline{H}}$, and satisfies $\delta \left(\overline{H}\right)=\left|\overline{H}\right|-\Delta \left(H\right)-1=q^2-1=\left|\overline{H}\right|(q^2-1)∕(q^2+q+1)$. Since ${lim}_{q\to \infty }(q^2-1)∕(q^2+q+1)=1$, it is impossible to give a sufficient condition using $\delta \left(\overline{H}\right)\ge c\left|\overline{H}\right|$ with a constant number $0<c<1$ for a graph $\overline{H}$ to have a spanning tree with diameter 3.

2 Proofs of Theorems 2 and 3

We first prove Theorem 2 by using Theorem 6.

Proof of Theorem 2

The case of $d=4$ will be proved in Proposition 8. Assume that $d\ge 6$ is an even integer, and $G$ satisfies $\delta \left(G\right)\ge 3\left|G\right|∕(d+2)$. Then by (2), we have $$\mathrm{radius}\left(G\right)\le \frac{3}{2}\cdot \frac{\left|G\right|}{\delta \left(G\right)+1}\le \frac{3}{2}\cdot \frac{\left|G\right|}{\frac{3\left|G\right|}{d+2}+1}=\frac{(d+2)}{2}\cdot \frac{3\left|G\right|}{3\left|G\right|+d+2}<\frac{d+2}{2}=\frac{d}{2}+1.$$ Since $d$ is even, the above inequality implies $\mathrm{radius}\left(G\right)\le d∕2$. Therefore $G$ has a spanning tree with diameter at most $d$. □

Proof of (2) of Theorem 3

Let $d\ge 5$ be an odd integer. Assume that $\delta \left(G\right)\ge 3\left|G\right|∕(d+1)$. Then $d^{\prime }=d-1$ is even and $G$ satisfies $\delta \left(G\right)\ge 3\left|G\right|∕(d^{\prime }+2)$, and thus by Theorem 2, $G$ has a spanning tree with diameter at most $d^{\prime }=d-1$. □

In order to prove (1) of Theorem 3, we need some notations. Let $G$ be a connected graph. For disjoint vertex sets $X$ and $Y$ of $G$, we write $E_G(X,Y)$ for the set of edges of $G$ joining a vertex of $X$ to a vertex of $Y$. For vertices $u$ and $v$, a vertex set $X$, and a positive integer $m$, let us define notations as follows. $$d_G(X,v)=d_G(v,X)≔\underset{x\in X}{min}{d}_G(x,v)$$$$Dis{k}^m\left(v\right)≔\{x\in V\left(G\right):d_G(v,x)\le m\}$$$$Dis{k}^m\left(X\right)≔\{y\in V\left(G\right):d_G(X,y)\le m\}$$$$Circl{e}^m\left(v\right):\{x\in V\left(G\right):d_G(v,x)=m\}$$

The following lemma is easy, but useful, and we often use it without mention. Moreover, it is clear that $Dis{k}^r\left(v\right)=V\left(G\right)$ if and only if the eccentricity of $v$ is at most $r$.

Lemma 7

Let $r$,$s$ and$d$ be positive integers. Let $G$ be a connected graph, and let $u$ be a vertex and $vw$ be an edge of $G$. Then the following two statements hold.

(i) If $Dis{k}^r\left(u\right)=V\left(G\right)$, then$G$ has a spanning tree with diameter at most $2r$. In particular, if $G$ has no spanning tree with diameter at most $2d$, then for any vertex $x$,$G$ has a vertex $y$ such that $d_G(x,y)\ge d+1$.

(ii) if $Dis{k}^s\left(\{v,w\}\right)=V\left(G\right)$, then$G$ has a spanning tree with diameter at most $2s+1$.

We begin with the proof of the case of $d=4$ in Theorem 2.

Proposition 8

If a connected graph $G$ satisfies $\delta \left(G\right)\ge 3\left|G\right|∕6=\left|G\right|∕2$, then$G$ has a spanning tree with diameter at most $4$.

Proof

Assume $\delta \left(G\right)\ge \left|G\right|∕2$. Let $v$ be a vertex of $G$, and $x$ be any vertex of $V\left(G\right)-N_G\left(v\right)$, if any. Then $N_G\left(v\right)\cap N_G\left(x\right)\ne 0̸$ by $\delta \left(G\right)\ge \left|G\right|∕2$, and so $d_G(v,x)=2$. Hence $Dis{k}^2\left(v\right)=V\left(G\right)$, and thus $G$ has a spanning tree with diameter at most 4 by Lemma 7. □

Proposition 9

If a connected graph $G$ satisfies $\delta \left(G\right)\ge 3\left|G\right|∕7$, then$G$ has a spanning tree with diameter at most $5$.

Proof

Suppose that a connected graph $G$ satisfies $\delta \left(G\right)\ge 3\left|G\right|∕7$, but has no spanning tree with diameter at most 5. The next claim follows from (i) of Lemma 7.

Claim 1 For each vertex $v$, $G$ has a vertex $u$ such that $d_G(v,u)=3$.

Claim 2 For two adjacent vertices $u$ and $v$, $|N_G\left(u\right)\cap N_G\left(v\right)|\ge 2\left|G\right|∕7$.

Proof

Assume that there exist two adjacent vertices $x$ and $y$ such that $|N_G\left(x\right)\cap N_G\left(y\right)|<2\left|G\right|∕7$. Then $$|N_G\left(x\right)\cup N_G\left(y\right)|=\left|N_G\left(x\right)\right|+\left|N_G\left(y\right)\right|-|N_G\left(x\right)\cap N_G\left(y\right)|>\frac{4\left|G\right|}{7}.$$Hence for every vertex $z\in V\left(G\right)-(N_G\left(x\right)\cup N_G\left(y\right))$, $N_G\left(z\right)\cap (N_G\left(x\right)\cup N_G\left(y\right))\ne 0̸$. This implies that $Dis{k}^2\left(\{x,y\}\right)=V\left(G\right)$. Hence $G$ has a spanning tree with diameter at most 5 by Lemma 7. This is a contradiction. Therefore the claim holds.

By Claim 1, we can take a path $(v_1,v_2,v_3,v_4)$ of length 3 such that $d_G(v_1,v_4)=3$. Then $(N_G\left(v_1\right)\cap N_G\left(v_2\right))\cap (N_G\left(v_3\right)\cap N_G\left(v_4\right))=0̸$ by $d_G(v_1,v_4)=3$. Let $W=(N_G\left(v_1\right)\cap N_G\left(v_2\right))\cup (N_G\left(v_3\right)\cap N_G\left(v_4\right))$. Then it follows from Claim 2 that $\left|W\right|\ge 2\times (2\left|G\right|∕7)=4\left|G\right|∕7$. Thus for every vertex $x\in V\left(G\right)-(W\cup \{v_1,v_2,v_3,v_4\})$, we have $N_G\left(x\right)\cap W\ne 0̸$, which implies $Dis{k}^2\left(\{v_2,v_3\}\right)=V\left(G\right)$. Hence by Lemma 7, $G$ has a spanning tree with diameter at most 5. This is a contradiction, and therefore the proposition is proved. □

Proposition 10

If a connected graph $G$ satisfies $\delta \left(G\right)\ge 3\left|G\right|∕9=\left|G\right|∕3$, then$G$ has a spanning tree with diameter at most $7$.

Proof

Suppose that a connected graph $G$ satisfies $\delta \left(G\right)\ge \left|G\right|∕3$, but has no spanning tree with diameter at most 7. The next claim holds as before.

Claim 1 For each vertex $v$ of $G$, there exists a vertex $u$ such that $d_G(v,u)=4$.

By Claim 1, we can take a path $(v_1,v_2,v_3,v_4)$ of length 3 such that $d_G(v_1,v_4)=3$. Then $N_G\left(v_1\right)\cap N_G\left(v_4\right)=0̸$, and so we obtain $$|N_G\left(v_1\right)\cup N_G\left(v_4\right)|\ge 2\times \frac{\left|G\right|}{3}=\frac{2\left|G\right|}{3}.$$Hence for every $x\in V\left(G\right)-(N_G\left(v_1\right)\cup N_G\left(v_4\right))$, $N_G\left(x\right)\cap (N_G\left(v_1\right)\cup N_G\left(v_4\right))\ne 0̸$, which implies $Dis{k}^3\left(\{v_2,v_3\}\right)=V\left(G\right)$, and thus $G$ has a spanning tree with diameter at most 7, a contradiction. Therefore the proposition holds. □

Proposition 11

If a connected graph $G$ satisfies $\delta \left(G\right)\ge 3\left|G\right|∕11$, then$G$ has a spanning tree with diameter at most $9$.

Proof

Suppose that a connected graph $G$ satisfies $\delta \left(G\right)\ge 3\left|G\right|∕11$, but has no spanning tree with diameter at most $9$. By Lemma 7, the next claim holds.

Claim 1 For every vertex $v$, there exists a vertex $u$ such that $d_G(v,u)=5$.

Claim 2 For every path $(v_1,v_2,v_3,v_4,v_5,v_6)$ with $d_G(v_1,v_6)=5$, it follows that $|N_G\left(v_3\right)\cap N_G\left(v_4\right)|<2\left|G\right|∕11$ and $|N_G\left(v_3\right)\cup N_G\left(v_4\right)|>4\left|G\right|∕11$.

Proof

Assume that $|N_G\left(v_3\right)\cap N_G\left(v_4\right)|\ge 2\left|G\right|∕11$. Then since $N_G\left(v_1\right)$, $N_G\left(v_3\right)\cap N_G\left(v_4\right)$ and $N_G\left(v_6\right)$ are pairwise disjoint, $U=N_G\left(v_1\right)\cup (N_G\left(v_3\right)\cap N_G\left(v_4\right))\cup N_G\left(v_6\right)$ satisfies $\left|U\right|\ge 8\left|G\right|∕11$. Hence for every vertex $x$, it follows that $N_G\left(x\right)\cap U\ne 0̸$, which implies $Dis{k}^4\left(\{v_3,v_4\}\right)=V\left(G\right)$, and so $G$ has a spanning tree with diameter at most 9, a contradiction. Thus $|N_G\left(v_3\right)\cap N_G\left(v_4\right)|<2\left|G\right|∕11$.

It follows from $|N_G\left(v_3\right)\cap N_G\left(v_4\right)|<2\left|G\right|∕11$ that $|N_G\left(v_3\right)\cup N_G\left(v_4\right)|=\left|N_G\left(v_3\right)\right|+\left|N_G\left(v_4\right)\right|-|N_G\left(v_3\right)\cap N_G\left(v_4\right)|>4\left|G\right|∕11$.

Claim 3 If there is a path $(v_1,v_2,\dots ,v_6)$ with $d_G(v_1,v_6)=5$, then either $|N_G\left(v_1\right)\cup N_G\left(v_2\right)|<4\left|G\right|∕11$ or $|N_G\left(v_5\right)\cup N_G\left(v_6\right)|<4\left|G\right|∕11$.

Proof

Assume that there exists a path $(v_1,v_2,\dots ,v_6)$ such that $d_G(v_1,v_6)=5$, $|N_G\left(v_1\right)\cup N_G\left(v_2\right)|\ge 4\left|G\right|∕11$ and $|N_G\left(v_5\right)\cup N_G\left(v_6\right)|\ge 4\left|G\right|∕11$. Let $U=(N_G\left(v_1\right)\cup N_G\left(v_2\right))\cup (N_G\left(v_5\right)\cup N_G\left(v_6\right))$. Then $\left|U\right|\ge 8\left|G\right|∕11$, and thus for every vertex $x$ of $G$, $N_G\left(x\right)\cap U\ne 0̸$, which implies $Dis{k}^4\left(\{v_3,v_4\}\right)=V\left(G\right)$. Hence $G$ has a spanning tree with diameter at most 9, a contradiction. Therefore the claim holds.

Claim 4 There exist no two vertices $v$ and $w$ such that $d_G(v,w)=6$.

Proof

Assume that there exist two vertices $v$ and $w$ such that $d_G(v,w)=6$. Let $(v=v_1,v_2,v_3,\dots ,v_7=w)$ be a path of length 6 connecting $v$ and $w$. Then $N_G\left(v_1\right)$, $N_G\left(v_4\right)$ and $N_G\left(v_7\right)$ are pairwise disjoint. So $X=N_G\left(v_1\right)\cup N_G\left(v_4\right)\cup N_G\left(v_7\right)$ satisfies $\left|X\right|\ge 9\left|G\right|∕11$. Thus every vertex $x$ of $G$ satisfies $N_G\left(x\right)\cap X\ne 0̸$, which implies $d_G(x,v_4)\le 5$. Moreover, if $d_G(x,v_4)=5$, then there exists a path of length 5 that connects $x$ and $v_4$ and passes through $v_1$ or $v_7$. If $d_G(x,v_4)\le 4$ for every $x\in V\left(G\right)$, then $G$ has a spanning tree with diameter at most 8. If for every vertex $z$ with $d_G(z,v_4)=5$, there is a path of length 5 that connects $z$ and $v_4$ and passes through $v_1$, then $G$ has a spanning tree $T$ with diameter 9, in which $d_T(z,v_1)=2$ for every vertex $z$ with $d_G(z,v_4)=5$. By the symmetry of $v_1$ and $v_7$, we may assume that there exist two vertices $x_1$ and $y_1$ such that $d_G(x_1,v_4)=5$, $d_G(y_1,v_4)=5$, there is a path $P(x_1,v_4)$ of length 5 connecting $x_1$ and $v_4$ and passing through $v_1$, and there is a path $P(y_1,v_4)$ of length 5 connecting $y_1$ and $v_4$ and passing through $v_7$.

Let $x_2$ be a vertex in the path $P(x_1,v_4)$ adjacent to both $x_1$ and $v_1$, and $y_2$ be a vertex in the path $P(y_1,v_4)$ adjacent to both $y_1$ and $v_7$. We shall show that $N_G\left(x_1\right)$, $N_G\left(v_2\right)$, $N_G\left(v_5\right)$ and $N_G\left(y_2\right)$ are pairwise disjoint. It is obvious that $d_G(x_1,v_2)=3$, $d_G(v_2,v_5)=3$ and $d_G(v_5,y_2)=3$. Moreover, it follows that $d_G(x_1,v_5)\ge d_G(x_1,v_4)-d_G(v_4,v_5)=4$ and $d_G(v_2,y_2)\ge d_G(v_2,v_7)-d_G(v_7,y_2)=4$. If $d_G(x_1,y_2)\le 2$, then $6=d_G(v_1,v_7)\le d_G(v_1,x_1)+d_G(x_1,y_2)+d_G(y_2,v_7)=5$, a contradiction. Hence $d_G(x_1,y_2)\ge 3$. Therefore $N_G\left(x_1\right)$, $N_G\left(v_2\right)$, $N_G\left(v_5\right)$ and $N_G\left(y_2\right)$ are pairwise disjoint. This is a contradiction since every set contains at least $3\left|G\right|∕11$ vertices of $G$.

Claim 5 Let $u$ and $v$ be two adjacent vertices for which there is a path $(s_1,s_2,u,v,t_2,t_1)$ with $d_G(s_1,t_1)=5$. Then there exists no vertex $w$ such that $d_G(u,w)=5$ and $d_G(v,w)=5$.

Proof

Assume that there exists a vertex $w$ such that $d_G(u,w)=5$ and $d_G(v,w)=5$. Let $(u=u_1,u_2,u_3,\dots ,u_6=w)$ be a path of length 5 connecting $u$ and $w$. Since $d_G(v,w)=5\le d_G(v,u_4)+d_G(u_4,w)$, it follows that $d_G(v,u_4)\ge 3$. It follows from $d_G(s_1,t_1)=5$ that either $d_G(s_1,u_4)\ge 3$ or $d_G(t_1,u_4)\ge 3$. Assume first $d_G(s_1,u_4)\ge 3$. Then $N_G\left(s_1\right)$, $N_G\left(v\right)$ and $N_G\left(u_4\right)$ are pairwise disjoint. Thus for every vertex $x\in V\left(G\right)$, it follows that $N_G\left(x\right)\cap (N_G\left(s_1\right)\cup N_G\left(v\right)\cup N_G\left(u_4\right))\ne 0̸$, which implies $Dis{k}^4\left(\{u,u_2\}\right)=V\left(G\right)$. Therefore $G$ has a spanning tree with diameter at most 9. Hence $d_G(s_1,u_4)\le 2$ and $d_G(t_1,u_4)\ge 3$.

By $d_G(t_1,u_4)\ge 3$, it holds that $N_G\left(u\right)$, $N_G\left(u_4\right)$ and $N_G\left(t_1\right)$ are pairwise disjoint, and for every vertex $x$, it follows that $N_G\left(x\right)\cap (N_G\left(u\right)\cup N_G\left(u_4\right)\cup N_G\left(t_1\right))\ne 0̸$. If every vertex $y$ with $N_G\left(t_1\right)\cap N_G\left(y\right)\ne 0̸$ satisfies $d_G(y,u)\le 4$, then $Dis{k}^4\left(\{u,u_2\}\right)=V\left(G\right)$, and so $G$ has a spanning tree with diameter at most 9. Hence we may assume that there exists a vertex $y_1$ such that $d_G(y_1,u)=5$ and there is a path of length $5$ that connects $y_1$ and $u$ and passes through $t_1$. By Claim 1, it follows that $|N_G\left(t_1\right)\cup N_G\left(t_2\right)|>4\left|G\right|∕11$.

Let $(v=v_1,v_2,v_3,\dots ,v_6=w)$ be a path of length 5 connecting $v$ and $w$. By the symmetry of $u$ and $v$, we can similarly show that there exists a vertex $x_1$ such that $d_G(x_1,s_1)=2$, $d_G(x_1,v)=5$ and $|N_G\left(s_1\right)\cup N_G\left(s_2\right)|>4\left|G\right|∕11$.

Since $d_G(s_1,t_1)=5$, the above fact that $|N_G\left(t_1\right)\cup N_G\left(t_2\right)|>4\left|G\right|∕11$ and $|N_G\left(s_1\right)\cup N_G\left(s_2\right)|>4\left|G\right|∕11$ contradicts Claim 3. Therefore the claim is proved.

By Claim 1, there exist two adjacent vertices $u$ and $v$ such that there exists a path $(s_1,s_2,u,v,t_2,t_1)$ of length 5 and $d_G(s_1,t_1)=5$. If $Dis{k}^4\left(\{u,v\}\right)=V\left(G\right)$, then $G$ has a spanning tree with diameter 9. Thus there exists a vertex $w$ such that $d_G(u,w)\ge 5$ and $d_G(v,w)\ge 5$. By Claim 3, we may assume that $w$ satisfies $d_G(u,w)=5$ and $d_G(v,w)=5$. But this contradicts Claim 5. Consequently Proposition 11 is proved. □