The spectral characterization of the connected multicone graphs

Abstract

A multicone graph is defined to be the join of a clique and a regular graph. Let $w$, $n$ and $m$ be natural numbers, and let $K_w$ and $K_{n,n}$ denote a complete graph and a complete bipartite graph, respectively. In this work, it is proved that connected multicone graphs $K_w▽m{K}_{n,n}$, natural generalizations of friendship graphs, are determined by their adjacency spectra as well as their Laplacian spectra. Also, we show that the complement of multicone graphs $K_w▽K_{n,n}$ is determined by their adjacency spectra. Furthermore, we prove that any graph cospectral with a multicone graph $K_w▽m{K}_{n,n}$ is perfect with respect to its adjacency (Laplacian) spectra. At the end of the paper, we pose two problems for further research.

Keywords:

• Adjacency spectrum
• Laplacian spectrum
• Multicone graph
• Friendship graph
• DS graph

1 Introduction

Throughout the paper, except in Section 3.2, $G=(V,E)$ is a connected undirected simple graph with $V=\left\{v_1,v_2,\dots v_n\right\}$ and $E=\left\{e_1,e_2,\dots ,e_m\right\}$. In this section we recall some definitions that will be used in the paper. For terminology and notation not defined here, we refer the readers to [1–4]. The notation $N\left(v\right)$ is used to denote as the neighbors of vertex $v$. The degree of vertex $v$, written $d\left(v\right)$, is $d\left(v\right)=\left|N\left(v\right)\right|$. We use $\Delta \left(G\right)$ and $\delta \left(G\right)$ to indicate the maximum and minimum degrees of $G$, respectively. A graph is called bidegreed if the set of degrees of vertices consists of exactly two distinct elements. Let the adjacency matrix, degree matrix of $G$ be $A\left(G\right)=\left[a_{ij}\right]$, $D\left(G\right)=diag\left\{d\left(v_1\right),d\left(v_2\right),\dots ,d\left(v_n\right)\right\}$, respectively. The Laplacian matrix of $G$ is $L\left(G\right)=D\left(G\right)-A\left(G\right)$ and the signless Laplacian matrix of $G$ is $SL\left(G\right)=D\left(G\right)+A\left(G\right)$. Clearly, $L\left(G\right)$ and $SL\left(G\right)$ are real symmetric matrices. We denote the characteristic polynomial $det(\lambda I-A)$ of $G$ by $P_G\left(\lambda \right)$. The adjacency spectrum of $G$, denoted by ${\mathrm{Spec}}_A\left(G\right)$, is the multiset of eigenvalues of $A\left(G\right)$. Since $A\left(G\right)$ is symmetric, its eigenvalues are real. The union of two graphs $G$ and $H$ is the graph whose vertex set is $V\left(G\right)\cup V\left(H\right)$ and whose edge set is $E\left(G\right)\cup E\left(H\right)$. We denote this graph by $G▽H$. The join of two graphs $G$ and $H$, denoted by $G▽H$, is created by adding edges between $G$ and $H$ so that every vertex in $G$ is adjacent to every vertex in $H$. ${\mathrm{Spec}}_A\left(G\right)=\left\{\left[{\lambda }_1\right]{}^{m_1},{\left[{\lambda }_2\right]}^{m_2},\dots ,{\left[{\lambda }_n\right]}^{m_n}\right\}$ of eigenvalues of $A\left(G\right)$ is called the adjacency spectrum of $G$, where $m_i$ denote the multiplicity of eigenvalue ${\lambda }_i$(For ${\mathrm{Spec}}_L\left(G\right)$ the definition is similar). A graph $H$ is said to be determined by its spectrum or DS for short, if there is no non-isomorphic graph with the same adjacency (respectively, Laplacian) spectrum.

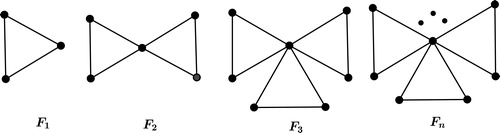
Determining which graphs are DS is a hard problem. About the background of the research question “which graph are determined by their spectrum?”, one can refer to [5,6]. The authors in [5] conjectured that nearly all graphs are determined by their spectra. However, the set of graphs that are known to be determined by their spectra is very small. Hence finding classes of graphs that are determined by their spectra can be an interesting and significant problem. A spectral characterization of some classes of multicone graphs was studied in [7]. The authors [7,8] conjectured that friendship graph $F_n=K_1▽n{K}_2$ (see Fig. 1) is DS with respect to their adjacency spectra. This conjecture caused some activities on the adjacency spectral characterization of $F_n$. Eventually, the authors [9] proved that if $G$ is a graph cospectral with a friendship graph $F_n$ and $n\ne 16$, then $G$ is isomorphic to $F_n$. Abdian and Mirafzal [10] characterized new classes of multicone graphs. These authors proved that the join of an arbitrary complete graph with an arbitrary Cocktail-Party graph is determined by its adjacency spectra as well as its Laplacian spectra. They also conjectured that these multicone graphs are determined by their signless Laplacian spectra. Abdian [11] characterized two classes of multicone graphs and showed that the join of an arbitrary complete graph and the generalized quadrangle graph $GQ(2,1)$ or $GQ(2,2)$ is determined by both its adjacency and its Laplacian spectra. This author also proposed four conjectures about adjacency spectrum of complement and signless Laplacian spectrum of these multicone graphs. In [12], the author showed that multicone graphs $K_w▽P_9$ and $K_w▽S$ are determined by their adjacency and their Laplacian spectra, where $P_9$ and $S$ denote the Paley graph of order 9 and the Schläfli graph, respectively. Also, this author conjectured that these multicone graphs are determined by their signless Laplacian spectra. For seeing some multicone graphs which have been characterized so far refer to [10–22].

Fig. 1 Examples of friendship graphs.

The organization of the paper is as follows. In Section 2, we review some basic information and preliminaries. In Section 3 (Sections 3.0.1 and 3.0.2), we show that any connected graph cospectral with one of multicone graphs $K_w▽m{K}_{n,n}$ is determined by its adjacency spectra. In Section 3.1, we prove that these graphs are determined by their Laplacian spectra. In Section 3.2, we prove that the complement of these graphs is DS with respect to their adjacency spectra. In Section 3.3, we show that any graph cospectral with one of these graphs must be perfect. In Section 4, we review our results in the previous sections. In conclusion we propose two conjectures for further research.

2 Notation and preliminaries

In this section, we give some results which will play a crucial role throughout the paper.

Theorem 2.1

[2,7] If $G$ is a graph with $n$ vertices,$m$ edges, minimum degree $\delta$, and spectral radius $\rho$, then $$\rho \le \frac{\delta -1}{2}+\sqrt{2m-n\delta +\frac{{(\delta +1)}^2}{4}}.$$Equality holds if and only if $G$ is either regular or is bi-regular with $\Delta =n-1$.

The next theorem gives a characterization of some graphs with three distinct eigenvalues.

Theorem 2.2

[18,23] A graph has exactly one positive eigenvalue if and only if it is a complete multipartite graph with possibly some isolated vertices.

Theorem 2.3

[3] Let $G$ be a graph with spectral radius $\rho$. Then the following statements are equivalent:

(1) $G$ is regular.

(2) $\rho$ is the average vertex degree in $G$.

(3) ${(1,1,\dots ,1)}^{\mathsf{T}}$ is an eigenvector for $\rho$.

Theorem 2.4

[1] If $G$ is an$r$-regular graph with eigenvalues ${\lambda }_1(=r),{\lambda }_2,\dots ,{\lambda }_n$, then$n-1-{\lambda }_1,-1-{\lambda }_2,\dots ,-1-{\lambda }_n$ are the eigenvalues of the complement $\overline{G}$ of $G$.

Theorem 2.5

[23] If $G$ is not regular and has exactly three eigenvalues ${\theta }_1>{\theta }_2>{\theta }_3$, then:

(a) $G$ has diameter $2$;

(b) if ${\theta }_1$ is not an integer, then $G$ is complete bipartite;

(c) ${\theta }_2\ge 0$ with equality if and only if $G$ is complete bipartite;

(d) ${\theta }_3<-2$.

Theorem 2.6

[2] For $i=1,2$, let$G_i$ be an$r_i$-regular graph of order $n_i$. Then the characteristic polynomial of their join is $$P_{G_1▿G_2}\left(x\right)=P_{G_1}\left(x\right)P_{G_2}\left(x\right)(1-\frac{n_1{n}_2}{(x-r_1)(x-r_2)}).$$

Theorem 2.7

[3,18] The following statements are equivalent for a nontrivial graph$G$ with characteristic polynomial $P_G\left(x\right)={\sum }_{i=0}^n{c}_i{x}^i$, spectrum ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_n$, and spectral radius $\rho$.

(1) $G$ is bipartite.

(2) The coefficients $c_i$ for $i$ odd are all $0$.

(3) For each $i$,${\lambda }_{n+1-i}=-{\lambda }_i$.

(4) $\rho =-{\lambda }_n$.

Theorem 2.8

[2] If $j$ is a vertex of graph $G$, then $P_{G-j}\left(x\right)=P_G\left(x\right){\sum }_{i=1}^m\frac{{\alpha }_{ij}^2}{x-{\mu }_i}$, where $m$ and ${\alpha }_{ij}$ are the number of distinct eigenvalues and the main angle of graph$G$, respectively.

Proposition 2.1

[6] Let $G$ be a disconnected graph that is determined by the Laplacian spectrum. Then the cone over$G$, the graph$H$; that is, obtained from$G$ by adding one vertex that is adjacent to all vertices of $G$, is also determined by its Laplacian spectrum.

Theorem 2.9

[24] Let $G$ and$H$ be graphs with Laplacian spectra ${\alpha }_1\ge {\alpha }_2\ge \cdots \ge {\alpha }_n$ and ${\beta }_1\ge {\beta }_2\ge \cdots \ge {\beta }_k$, respectively. Then

(a) the Laplacian spectrum of the complement $\overline{G}$ is $n-{\alpha }_1,n-{\alpha }_2,\dots ,n-{\alpha }_n-1,0$, and

(b) the Laplacian spectrum of the join $G▿H$ is $n+k,k+{\alpha }_1,k+{\alpha }_2,\dots ,k+{\alpha }_n-1,n+{\beta }_1,n+{\beta }_2,\dots ,n+{\beta }_{k-1},0$.

Theorem 2.10

[10–13,24] The order $n$ of a graph $G$ is a Laplacian eigenvalue of $G$ if and only if $G$ is the join of two graphs.

Remark 1

It is well-known that $F_{16}=K_1▽16K_{1,1}$ is not determined by its adjacency spectrum (see the first paragraph after Corollary 2 of [9]). Therefore, in the case that ${Spec}_A\left(G\right)={Spec}_A(K_w▽K_{n,n})$, we always suppose that $G$ is connected.

3 Main results

The purpose of this section is to show that any graph cospectral with a multicone graph $K_w▽m{K}_{n,n}$ is regular or bidegreed.

3.0.1 Connected graphs cospectral with a multicone graph $K_w▽m{K}_{n,n}$

Proposition 3.1

The adjacency spectrum of multicone graph $K_w▽m{K}_{n,n}$ is

$$\left\{{\left[\frac{\Omega +\sqrt{{\Omega }^2-4\Gamma }}{2}\right]}^1,{\left[\frac{\Omega -\sqrt{{\Omega }^2-4\Gamma }}{2}\right]}^1,{\left[0\right]}^{(2n-2)m},{\left[-1\right]}^{w-1},{\left[n\right]}^{m-1},{\left[-n\right]}^m\right\},$$where $\Omega =w-1+n$ and $\Gamma =(w-1)n-2nmw$.

Proof

By Theorem 2.6 and ${\mathrm{Spec}}_A\left(m{K}_{n,n}\right)=\left\{{\left[-n\right]}^m,{\left[0\right]}^{(2n-2)m},{\left[n\right]}^m\right\}$, the proof is completed.□

Lemma 3.1

Let $G$ be a connected graph cospectral with a multicone graph $K_w▽m{K}_{n,n}$. Then $\delta \left(G\right)=w+n$.

Proof

Let $\delta \left(G\right)=w+n+y$, where $y$ is an integer number. First, it is clear that in this case the equality in Theorem 2.1 occurs, if and only if $y=0$. We claim that $y=0$. By contrary, we suppose that $y\ne 0$. It follows from Theorem 2.1 together with Proposition 3.1 that $$\varrho \left(G\right)=\frac{w+n-1+\sqrt{8k-4l(w+n)+{(w+n+1)}^2}}{2}<\frac{w+n-1+y+\sqrt{8k-4l(w+n)+{(w+n+1)}^2+y^2+(2w+2(n+1)-4l)y}}{2},$$ where the integer numbers $k$ and $l$ denote the number of edges and the number of vertices of the graph $G$, respectively.

For convenience, we let $B=8k-4l(w+n)+{(w+n+1)}^2\ge 0$ and $N=w+(n+1)-2l$, and also let $f\left(y\right)=y^2+2(w+(n+1)-2l)y=y^2+2Ny$.

Then clearly $$\sqrt{B}-\sqrt{B+f\left(y\right)}<y.$$

We consider two cases:

Case 1. $y<0$.

It is easy and straightforward to see that $|\sqrt{B}-\sqrt{B+f\left(y\right)}|>\left|y\right|$, since $y<0$.

Transposing and squaring yields $$2B+f\left(y\right)-2\sqrt{B(B+f\left(y\right))}>y^2.$$

Replacing $f\left(y\right)$ by $y^2+2Ny$, we get $$B+Ny>\sqrt{B(B+y^2+2Ny)}.$$Obviously $Ny\ge 0$. Squaring again and simplifying yields (1) $$N^2>B.$$(1)

Therefore, (2) $$k<\frac{l(l-1)}{2}.$$(2)

Therefore, if $y<0$, then $G$ is not a complete graph. Or if $\delta \left(G\right)<w+n$, then $G$ is not a complete graph $\left(†\right)$. On the other hand, if $y<0$ for any non-complete graph $G$ we always have $\delta \left(G\right)<w+n$ $\left(‡\right)$. Combining $\left(†\right)$ and $\left(‡\right)$ we get: $\delta \left(G\right)<w+n$ if and only if $G$ is not a complete graph. To put that another way, $\delta \left(G\right)>w+n$ if and only if $G$ is a complete graph. But, if $G$ is a complete graph, then $\delta \left(G\right)=w+1$. Hence, we have $\delta \left(G\right)=w+1>w+n$ and so $n<1$, a contradiction.

Case 2. $y>0$. In this case if $G$ is non-complete graph, then $\delta \left(G\right)>w+n$ (*).

On the other hand by a similar argument of Case 1 for $y>0$, if $\delta \left(G\right)>w+n$, then $G$ is not a complete graph (**). Combining (*) and (**) we have: $\delta \left(G\right)<w+n$ if and only if $G$ is a complete graph or $G$ is a complete graph if and only if $n>1$, a contradiction. So, we must have $y=0$. Therefore, the assertion holds. □

In the next lemma we show that if $m\ne 1$ or $n\ne 1$, then any graph cospectral with a multicone graph $K_w▽m{K}_{n,n}$ must be bidegreed.

Lemma 3.2

Let $G$ be a connected graph cospectral with a multicone graph $K_w▽m{K}_{n,n}$. Then $G$ is either regular or bidegreed, in which any vertex of $G$ is of degree $n+w$ or $w-1+2mn$.

Proof

By Theorems 2.1, 2.3 and Lemma 3.1 the proof is completed. □

In the following, we show that multicone graphs $K_1▽m{K}_{n,n}$ are DS with respect to their adjacency spectrum.

3.0.2 Connected graphs cospectral with the multicone graph $K_1▽m{K}_{n,n}$

Lemma 3.3

Any connected graph cospectral with the multicone graph$K_1▽m{K}_{n,n}$ is isomorphic to $K_1▽m{K}_{n,n}$.

Proof

Let $G$ be a graph cospectral with a multicone graph $K_1▽m{K}_{n,n}$. By Lemma 3.2, $G$ has one vertex of degree $2mn$, say $j$. Now, $P_G\left(x\right)=(x-{\mu }_1)(x-{\mu }_2){(x-{\mu }_3)}^{m-1}{(x-{\mu }_4)}^m{(x-{\mu }_5)}^{(2n-2)m}$, where ${\mu }_1=\frac{n+\sqrt{n^2+8nm}}{2}$, ${\mu }_2=\frac{n-\sqrt{n^2+8nm}}{2}$, ${\mu }_3=n$, ${\mu }_4=-n$ and ${\mu }_5=0$ and $P_G\left(x\right)$ is the characteristic polynomial of $G$. It follows from Theorem 2.8 that $P_{G-j}\left(x\right)={(x-{\mu }_5)}^{(2n-2)m-1}{(x-{\mu }_3)}^{m-2}{(x-{\mu }_4)}^{m-1}[{\alpha }_{1j}^{2}A+{\alpha }_{2j}^{2}B+{\alpha }_{3j}^{2}C+{\alpha }_{4j}^{2}D+{\alpha }_{5j}^{2}E]$, where $$A=(x-{\mu }_2)(x-{\mu }_3)(x-{\mu }_4)(x-{\mu }_5),$$$$B=(x-{\mu }_1)(x-{\mu }_3)(x-{\mu }_4)(x-{\mu }_5),$$$$C=(x-{\mu }_1)(x-{\mu }_2)(x-{\mu }_4)(x-{\mu }_5),$$$$D=(x-{\mu }_1)(x-{\mu }_2)(x-{\mu }_3)(x-{\mu }_5),$$$$E=(x-{\mu }_1)(x-{\mu }_2)(x-{\mu }_3)(x-{\mu }_4).$$ We know that $P_{G-j}\left(x\right)$ has $2mn$ roots (eigenvalues). Also, it is clear that $G-j$ is a $n$-regular graph (see Lemma 3.2). It is easy and straightforward to see that by removing the vertex $j$ the number of edges and the number of triangles that are removed of graph $G$ are equal to $2mn$ and $m{n}^2$, respectively. Now, by computing the number of the closed walks of lengths 1, 2 and 3 belonging to $G-j$ we have: $$\alpha +\beta +\gamma +n=-[(m-1){\mu }_4+(m-2){\mu }_3],$$$${\alpha }^2+{\beta }^2+{\gamma }^2+n^2=2m{n}^2-[(m-1){\mu }_4^2+(m-2){\mu }_3^2],$$$${\alpha }^3+{\beta }^3+{\gamma }^3+n^3=-[(m-1){\mu }_4^3+(m-2){\mu }_3^3],$$ where $\alpha$, $\beta$ and $\gamma$ are eigenvalues of $P_{G-j}\left(x\right)$. By solving the above equations, $\alpha =0$, $\beta =n$ and $\gamma =-n$. So, ${\mathrm{Spec}}_A(G-j)=\left\{{\left[-n\right]}^m,{\left[0\right]}^{(2n-2)m},{\left[n\right]}^m\right\}$. Obviously, graph with adjacency spectrum $\left\{{\left[-n\right]}^m,{\left[0\right]}^{(2n-2)m},{\left[n\right]}^m\right\}$ is a regular graph and also it has three distinct eigenvalues. Therefore, $G-j$ is a strongly regular graph. So, $G-j\cong m{K}_{n,n}$ (see Proposition 10 (i) of [5]). Hence $G\cong K_1▽m{K}_{n,n}$. Thus the result follows. □

Hitherto, we have shown that multicone graphs $K_1▽m{K}_{n,n}$ are DS. The natural question is; what happens for multicone graphs $K_w▽m{K}_{n,n}$? we answer this question in the next theorem.

Theorem 3.1

Let $G$ be a connected graph. If ${\mathrm{Spec}}_A\left(G\right)={\mathrm{Spec}}_A(K_w▽m{K}_{n,n})$, then $G\cong K_w▽m{K}_{n,n}$.

Proof

We solve the problem by induction on $w$. If $w=1$, there is nothing to prove. Let the claim be true for $w$; that is, if ${\mathrm{Spec}}_A\left(G_1\right)={\mathrm{Spec}}_A(K_w▽m{K}_{n,n})$, then $G_1\cong K_w▽m{K}_{n,n}$, where $G_1$ is an arbitrary graph cospectral with a multicone graph $K_w▽m{K}_{n,n}$. We show that ${\mathrm{Spec}}_A\left(G\right)=Spe{c}_A(K_{w+1}▽m{K}_{n,n})$, implies that $G\cong K_{w+1}▽m{K}_{n,n}$. By Lemma 3.2 $G_1$ has $2m$ vertices of degree $n+w$ and $w$ vertices of degree $w-1+2mn$. Also from this lemma follows that $G$ has $2m$ vertices of degree $n+w+1$ and $w+1$ vertices of degree $w+2mn$. On the other hand, $G$ has one vertex and $w+2mn$ edges more than $G_1$. So, we must have $G\cong K_1▽G_1$. Consequently, the inductive hypothesis completes the proof.□

In the following, we present an alternate proof of Theorem 3.1.

Alternate proof of Theorem 3.1

By Lemma 3.2, $G$ has graph $B$ as its subgraph in which degree of any vertex of $B$ is $w-1+2mn$. In other words, $G\cong K_w▽H$, where $H$ is a subgraph of $G$. Now, we remove vertices of $K_w$ and we consider $2mn$ other vertices. Degree of graph consisting of these vertices is $n$, say $H$. $H$ is regular and its degree of regularity is $n$ and multiplicity of $n$ is $m$. By Theorem 2.6, ${\mathrm{Spec}}_A\left(H\right)=\left\{{\left[-n\right]}^m,{\left[0\right]}^{(2n-2)m},{\left[n\right]}^m\right\}$. Now, Theorem 2.2 implies that ${\mathrm{Spec}}_A\left(H\right)={\mathrm{Spec}}_A\left(m{K}_{n,n}\right)$. This completes the proof. □

3.1 Connected graphs cospectral with a multicone graph $K_w▽m{K}_{n,n}$ with respect to Laplacian spectrum

In this subsection, we prove that any graph cospectral with a multicone graph $K_w▽m{K}_{n,n}$ is DS with respect to its Laplacian spectrum.

Theorem 3.2

Let $G$ be a graph. If ${\mathrm{Spec}}_L\left(G\right)={\mathrm{Spec}}_L(K_w▽m{K}_{n,n})$, then $G\cong K_w▽m{K}_{n,n}$.

Proof

It is clear that ${\mathrm{Spec}}_L\left(m{K}_{n,n}\right)=\left\{{\left[2n\right]}^m,{\left[n\right]}^{(2n-2)m},{\left[0\right]}^m\right\}$. We solve the problem by induction on $w$. If $w=1$, by Proposition 2.1 the proof is completed. Let the problem be true for $w$, that is, if ${\mathrm{Spec}}_L\left(G_1\right)={\mathrm{Spec}}_L(K_w▽m{K}_{n,n})$, then $G_1\cong K_w▽m{K}_{n,n}$, where $G_1$ is an arbitrary graph cospectral with a multicone graph $K_w▽m{K}_{n,n}$. We show that ${\mathrm{Spec}}_L\left(G\right)={\mathrm{Spec}}_L(K_{w+1}▽m{K}_{n,n})=\left\{{\left[w+2mn+1\right]}^{w+1},{\left[w+n+1\right]}^{(2n-2)m},{\left[2n+w+1\right]}^m,{\left[w+1\right]}^{m-1},{\left[0\right]}^1\right\}$ implies that $G\cong K_{w+1}▽m{K}_{n,n}$, where $G$ is a graph. It follows from Theorem 2.10 that $G_1$ and $G$ are the join of two graphs. On the other hand, ${\mathrm{Spec}}_L(K_1▽G_1)={\mathrm{Spec}}_L\left(G\right)={\mathrm{Spec}}_L(K_{w+1}▽m{K}_{n,n})$ and also $G$ has one vertex and $w+2mn$ edges more than $G_1$.Therefore, we must have $G\cong K_1▽G_1$. Now, the inductive hypothesis completes the proof. □

Corollary 3.1

Friendship graphs $F_n=K_1▽n{K}_2$ are DS with respect to their Laplacian spectrum.

In the following, we show that any graph cospectral with a complement of multicone graph $K_w▽K_{n,n}$ is DS with respect to its adjacency spectrum. Also, we show that complement of multicone graph $K_w▽m{K}_{1,1}$ is DS with respect to its adjacency spectrum, where $m\ne 2$.

3.2 Graphs cospectral with a complement of multicone graph $K_w▽K_{n,n}$

Proposition 3.2

Let $G$ be cospectral with a complement of multicone graph $K_w▽m{K}_{n,n}$. Then ${\mathrm{Spec}}_A\left(G\right)=\left\{{\left[2mn-n-1\right]}^1,{\left[-1\right]}^{(2n-2)m},{\left[-n-1\right]}^{m-1},{\left[n-1\right]}^m,{\left[0\right]}^w\right\}$.

Proof

By Theorem 2.4 the proof is straightforward. □

Lemma 3.4

Let $G$ be a graph and ${\mathrm{Spec}}_A\left(G\right)=\left\{{\left[n-1\right]}^{2m},{\left[0\right]}^w,{\left[-1\right]}^{2(n-1)m}\right\}$. Then $G\cong w{K}_1\cup 2m{K}_n$.

Proof

Firstly, we show that $G$ is disconnected. By contrary, we suppose that $G$ is connected. It is clear that $G$ cannot be regular. In this case, we conclude from Theorem 2.5 that $G$ is a complete bipartite graph. By Theorem 2.2, $n=2$ and so $G\cong 2m{K}_2$. This is a contradiction. Therefore, $G$ is disconnected. Hence $G=G_1\cup G_2\cup \cdots \cup G_k$, where $G_i$ ($1\le i\le k$) are connected components of $G$. We show that $G_i$ does not have distinct three eigenvalues. By contrary, we suppose that $G_j$ has three distinct eigenvalues. We consider two cases:

Case 1. $G_j$ is non-regular.

In this case, Theorem 2.5 implies that $G_j$ is a complete bipartite graph, that is, $G_j\cong K_{p,q}$, where $1\le j\le k$ and $p$, $q$ are natural numbers. Hence $n=2$ and also $G_j\cong K_{1,1}\cong K_2$ and so $G_j$ cannot have three distinct eigenvalues.

Case 2. $G_j$ is regular.

It is clear $G_j$ has exactly one positive eigenvalue. On the other hand, we conclude from Theorem 2.2 that $G_j=G_1\cup w{K}_1$, where $G_1$ is a complete multipartite graph. Obviously, $w=0$ and so $G_j\cong K_{\underset{ntimes}{\underbrace{1,1,1,\dots ,1}}}\cong K_n$ and so $G_j$ cannot have three distinct eigenvalues. By what has been proved hitherto, any connected component of $G$ has either one or two eigenvalue(s). In other words, any connected component of $G$ is either isolated vertex or a complete graph. Hence $G\cong w{K}_1\cup 2m{K}_n$ $\square$

Theorem 3.3

Any graph cospectral with $\overline{K_w▽K_{n,n}}$ is isomorphic to $\overline{K_w▽K_{n,n}}$.

Proof

If graph $G$ is cospectral with the $\overline{K_w▽K_{n,n}}$, then ${\mathrm{Spec}}_A\left(G\right)=\left\{{\left[n-1\right]}^2,{\left[0\right]}^w,{\left[-1\right]}^{2n-2}\right\}$. Now, By Lemma 3.4 the proof is straightforward. □

In $\left[5\right]$, it is proved that any graph cospectral with a complement of friendship graph $F_n$, $\overline{F_n}=\overline{K_1▽n{K}_2}$, is DS, where $n\ne 2$. Now, we generalize this fact and we show that if $m\ne 2$, then complement of multicone graph $K_w▽m{K}_{1,1}$, $\overline{K_w▽m{K}_{1,1}}$, is DS with respect to its adjacency spectrum.

Proposition 3.3

Let $G$ be a graph cospectral with the graph $\overline{K_w▽2K_{1,1}}$.

$G\cong K_{2,2}\cup w{K}_1$ if and only if $G$ is disconnected.

Proof

($⟹$) Is trivial.

($⟸$) By Lemma 2.4, $G$ is a bipartite graph. By Theorem 2.2 $G\cong w{K}_1\cup G_1$, where $G_1$ is a subgraph of $G$. By Theorem 2.10 $G_1$ is a complete bipartite graph and so $G_1\cong K_{2,2}$. This completes the proof.□

Proposition 3.4

Let $G$ be a graph cospectral with $\overline{K_w▽2K_{1,1}}$.

$G$ is connected if and only if $G\cong K_{1,4}$ and $w=1$.

Proof

$(⟸)$ Is trivial.

$(⟹)$ By Theorem 2.5 the proof is completed. □

Theorem 3.4

Let $G$ be a graph and ${\mathrm{Spec}}_A\left(G\right)={\mathrm{Spec}}_A\left(\overline{K_w▽m{K}_{1,1}}\right)$. Then $G$ is DS, where $m\ne 2$.

Proof

If $m=1$, there is nothing to prove. Hence we let $m\ge 3$. It follows from Theorem 2.5 that $G$ is not connected and also Theorem 2.2 implies that $G=G_1\cup s{K}_1$, where $s$ is a natural number. We show that $G_1$ is a regular graph. By contrary, we suppose that $G_1$ is a non-regular graph. It follows from Theorem 2.5 that $G_1$ is a complete bipartite graph and so $G$ is a bipartite graph. This is a contradiction, since $G$ contains at least a triangle. Hence $G_1$ is a regular graph and so $\varrho \left(G_1\right)=2n-2$. Now, from Theorem 2.2 we conclude that $G_1$ is a multibipartite graph. Hence $G_1\cong K{2,2,\dots ,2}_{mtimes}$ and so $G=G_1\cup w{K}_1\cong K_{2,2,\dots ,2mtimes}\cup w{K}_1\cong \overline{K_w▽m{K}_{1,1}}$. □

Suppose $\chi \left(G\right)$ and $\omega \left(G\right)$ are chromatic number and clique number of graph $G$, respectively. A graph is perfect if $\chi \left(H\right)=\omega \left(H\right)$ for every induced subgraph $H$ of $G$. It is proved that a graph $G$ is perfect if and only if $G$ is Berge; that is, it contains no odd hole or antihole as induced subgraph, where odd hole and antihole are odd cycle, $C_m$ for $m\ge 5$, and its complement, respectively. Also, in $1972$ Lovásaz proved that, a graph is perfect if and only if its complement is perfect [25].

3.3 Some graphical results on multicone graphs $K_w▽m{K}_{n,n}$

Theorem 3.5

Let graph $G$ be a graph cospectral with a multicone graph $K_w▽m{K}_{n,n}$. Then $G$ and $\overline{G}$ are perfect.

Proof

This follows Theorem 3.1 and the fact that $K_w▽m{K}_{n,n}$ is perfect .□

Theorem 3.6

Let ${\mathrm{Spec}}_L\left(G\right)={\mathrm{Spec}}_L(K_w▽m{K}_{n,n})$. Then $G$ and $\overline{G}$ are perfect.

Proof

This follows Theorem 3.2 and the fact that $K_w▽m{K}_{n,n}$ is perfect. □

4 Concluding remarks and open problems

In this work, it is proved that multicone graphs $K_w▽m{K}_{n,n}$ are DS with respect to their adjacency spectra as well as their Laplacian spectra. Also, we shown that if $m\ne 2$, then any graph cospectral with a complement of multicone graph $K_w▽K_{n,n}$ is DS with respect to its adjacency spectra. Since multicone graphs $K_w▽m{K}_{n,n}$ are a natural generalization of friendship graphs and the friendship graphs are DS with respect to their signless Laplacian spectra, we pose two problems for further study.

Conjecture 1

Any graph cospectral with a complement of multicone graph$K_w▽m{K}_{n,n}$ is DS, where $m\ne 2$.

Conjecture 2

Multicone graphs $K_w▽m{K}_{n,n}$ are DS with respect to their signless Laplacian spectrum.