-shaped point set embeddings of high-degree plane graphs

Abstract

A point set embedding of a given plane graph $G$ on a given point set $P$ on a $2D$ plane is a drawing of $G$ where each vertex is drawn on a point in $P$. An orthogonal point set embedding of a plane graph $G$ is a point set embedding of $G$ such that each edge is drawn as a sequence of horizontal and vertical line segments. A plane graph of the maximum degree five or more does not admit an orthogonal point set embedding. To deal with plane graphs of the maximum degree five or more, in this paper we introduce “L-shaped point set embeddings”. An L-shaped point set embedding of a plane graph $G$ on a point set $P$ is a point set embedding of $G$ on $P$ such that each edge is drawn by a sequence of two straight-line segments which create a 90° angle at their common end. In this paper we consider $L$-shaped point set embeddings of trees and Halin Graphs. Let $P$ be a point set of $n$ points on a $2D$ plane such that no two points in $P$ lie on a horizontal or on a vertical line. We show that every tree of $n$ vertices as well as every Halin graph of $n$ vertices has an L-shaped point set embedding on $P$.

Keywords:

• Point set embedding
• Orthogonal point set embedding
• $L$-shaped point set embedding

1 Introduction

A plane graph is a planar graph with a fixed planar embedding. An orthogonal drawing of a plane graph $G$ is a drawing of $G$ such that each vertex is drawn as a point, each edge is drawn as a sequence of alternate horizontal and vertical line segments, and any two edges do not cross except at their common end. Orthogonal drawings of plane graphs have been extensively studied in literature due to their practical applications in circuit schematics, VLSI layouts, aesthetic layout of diagrams and computational geometry [1–5].

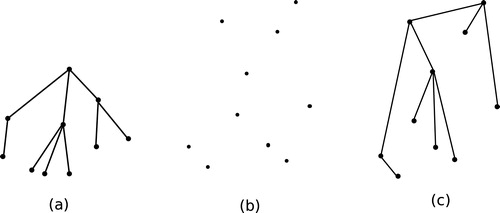
A point set embedding of a given plane graph $G$ on a given point set $P$ is a drawing of $G$ where each vertex is drawn on a point in $P$. Fig. 1(c) illustrates an example of a point set embedding of the tree shown in Fig. 1(a).

Fig. 1 (a) A tree, (b) a point set and (c) a point set embedding of the tree.

An orthogonal point-set embedding of a plane graph $G$ on a set $P$ of points on a $2D$ plane is a point set embedding of $G$ on $P$ such that each edge is drawn as a sequence of alternate horizontal and vertical line segments and any two edges do not cross except at their common end. Thus an orthogonal point-set embedding of a plane graph $G$ is an orthogonal drawing of $G$ on a given point set. Several researchers have worked on orthogonal point-set embeddings [6–8]. Di Giacomo et al. [6] have studied a special type of orthogonal point set embeddings which they called $L$-shaped point set embeddings where every edge required to be $L$-shaped. $L$-shaped point set embeddings have important practical applications in the field of VLSI layout where connectors are only allowed to be $L$-shaped for some specified functions. Fig. 2 illustrates different examples of point set embeddings of graphs.

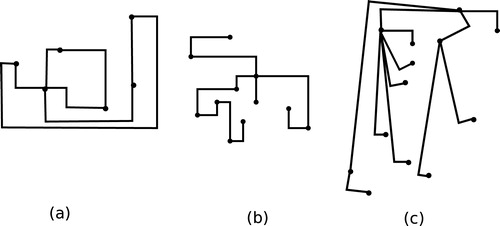
Fig. 2 (a) An orthogonal point-set embedding a graph, (b) an $L$-shaped point set embedding of a tree and (c) an $L$-shaped point set embedding for high degree plane graph.

Di Giacomo et al. [6] have shown that every tree of $n$ vertices and maximum degree four has $L$-shaped point set embeddings on a diagonal point set of $n$ points and on a 1-spaced point set of $n^2-2n+2$ points where 1-spaced point set is defined as a point set on a grid such that the horizontal and vertical distance of any two points is at least 1. They have also shown that every caterpillar of $n$ vertices and maximum degree four has an $L$-shaped point set embedding on 1-spaced point set of $3n-2$ points. Kano and Suzuki [7] have studied the problem of $L$-shaped point set embeddings on points in general position and have shown that every tree of $n$ vertices and maximum degree three with the property that all the vertices of degree 3 are contained in a path has an $L$-shaped point set embedding on a point set of $n$ points in general position.

In this paper we generalize $L$-shaped point set embeddings for high degree plane graphs where each edge is drawn by a sequence of two straight-line segments which create a90° angle at their common end. Note that the definition of $L$-shape in our case is different from the definition $L$-shape used in previous works. The two straight-line segments which constitute the $L$-shape are not necessity horizontal and vertical in our case (see Fig. 2(c)). We show that every tree of $n$ vertices as well as every Halin graph of $n$ vertices admits plane $L$-shaped point set embeddings on a $2D$ point set $P$ of $n$ points such that no two points in $P$ lie on a horizontal or on a vertical line. An $L$-shaped point set embedding of a high degree plane graph may find its applications in implementing circuits with prefabricated active devices and $L$-shaped connectors having variable arm lengths.

The remaining of the paper is organized as follows. Section 2 presents some definitions. Section 3 gives an algorithm that admits an $L$-shaped point set embedding of a tree. Section 4 gives an algorithm that admits an $L$-shaped point set embedding of a Halin graph. Finally, Section 5 contains concluding remarks and directions for further research in this field.

2 Preliminaries

In this section we present some terminologies and definitions which will be used throughout the paper. For the graph theoretic definitions which have not been described here, see [1,9].

A graph is planar if it can be embedded in the plane without edge crossing except at the vertices where the edges are incident. A plane graph is a planar graph with a fixed planar embedding. A plane graph divides the plane into connected regions called faces. The unbounded region is called the outer face; the other faces are called inner faces. The cycle that lies on the outer face is called outer cycle. The edges in the outer cycle are called outer edges.

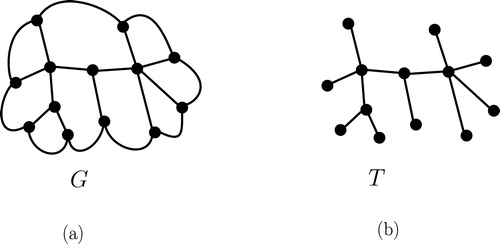
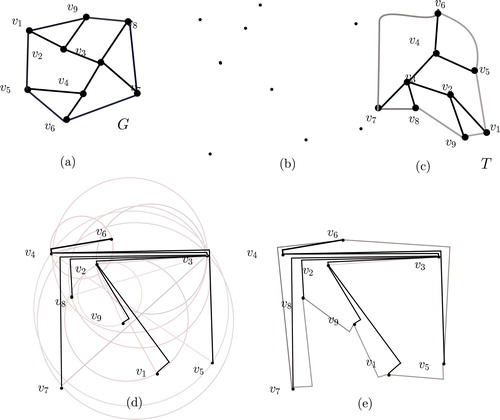
A Halin graph is a connected planar graph that consists of an unrooted tree and a cycle connecting the leaves of the tree. A Halin graph is constructed as follows. Let $T$ be a tree with more than three vertices embedded in the plane. Then a Halin graph is constructed by adding to $T$ a cycle through each of its leaves, such that the augmented graph remains planar. We call $T$ the core tree of the Halin graph. Fig. 3(a) shows a Halin graph and Fig. 3(b) shows the core tree of the Halin graph.

Fig. 3 (a) A Halin graph and (b) the core tree of the Halin graph.

The center of a tree $T$ is either a single node or an edge, which is obtained by repeatedly deleting all the nodes of degree one, until a single node or an edge is left. The distance between two vertices of a tree is the length (in edges) of the shortest path between these vertices. The diameter is the longest path between two nodes in a tree. The length of path between two nodes is represented by the number of edges between them.

Let $T$ be an ordered rooted tree with root $r$ whose children are ordered from left to right. Let $r_1,r_2,\dots ,r_k$ be the children of $r$ and $T_1,T_2,\dots ,T_k$ are the subtrees at rooted $r_1,r_2,\dots ,r_k$, respectively ordered in this way from left to right in $T$. For a vertex $v$ of $T$, we denote by $n\left(v\right)$ the number of vertices in the subtree rooted at $v$.

3 $L$-shaped point set embeddings of trees

In this section we show that any tree of $n$ vertices admits a plane $L$-shaped point set embedding whose vertices are given points in the plane, no two of which lie on the same horizontal or vertical line as in the following theorem.

Theorem 1

Let $T$ be a tree and let $P$ be a set of points where no two points lie on the same horizontal or vertical line. Then every $T$ admits an $L$ -shaped point set embedding on $P$ .

Proof

We give a constructive proof as follows. Let $T$ be a tree and let $P$ be a set of points where no two points lie on the same horizontal or vertical line. We first make $T$ an ordered rooted tree by taking an arbitrary node as the root of $T$ and ordering the children of each vertex in a counter clockwise order which reflects the plane embedding of $T$. We now label each node $v$ of $T$ by number $n\left(v\right)$ of vertices in the subtree rooted at $v$. We next place root $r$ to the topmost point $p_t$ of $P$. Let $r_1,r_2,\dots ,r_k$ be the children of $r$ and $T_1,T_2,\dots ,T_k$ are the subtrees at rooted $r_1,r_2,\dots ,r_k$, respectively ordered in this way from left to right in $T$. 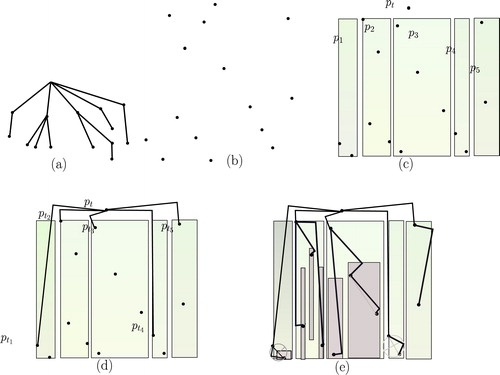We then partition the points of $P-\left\{p_t\right\}$ into vertical strips $P_1,P_2,\dots ,P_k$ from leftside such that $P_i,1\le i\le k$, contains $n\left(r_i\right)$ vertices, as illustrated in Fig. 4(c).

Let $p_{t_1},p_{t_2},\dots ,p_{t_k}$ be the topmost point of $P_1,P_2,\dots ,P_k$, respectively. We now connect $p_t$ to each of $p_{t_1},p_{t_2},\dots ,p_{t_k}$ by an $L$-shaped edge as follows. We consider the distance between these two points as the diameter of a circle and connect two points by two line segments which touch at circumference of the circle. Thus the angle at the common end of the two straight-line segments is 90°.

If $p_{t_i}$ of $P_i$ is situated at left from $p_t$ then we draw the $L$-shaped edge at left side of $p_t$ and if $p_{t_i}$ of $P_i$ is situated at right from $p_t$ then we draw the $L$-shaped edge at right side of $p_t$ as illustrated in Fig. 4(d). We recursively draw the remaining edges. One can observe that the resulting $L$-shaped point set embedding is a tree as illustrated in Fig. 4(e).

Since we make $T$ an ordered rooted tree, find ordering of the children, place every node of the tree on the fixed point according to ordering and no two points lie on the same horizontal or vertical line, there is no possibility to cross among the $L$-shaped edges. □

Fig. 4 (a) A tree, (b) a point set, (c) partitioned vertical strips $P_1,P_2,\dots ,P_k$, (d) $L$-shaped edges among $p_t$ to $p_{t_1},p_{t_2},\dots ,p_{t_k}$ and (e) an $L$-shaped point set embedding of the tree.

We call the algorithm described in the proof of Theorem 1 for finding $L$-shaped point set embeddings of trees Algorithm $L$-shaped_Draw_Tree. One can implement Algorithm $L$-shaped_Draw_Tree as follows. Using bottom-up computation on the tree, one can compute the labels of each vertex of the tree in $O\left(n\right)$ time. First construct a linked list of points sorted according to their $x$-coordinates in $O(nlogn)$ time and find the point $p_t$ with the highest $y$-coordinate and remove it from the linked list in $O\left(n\right)$ time. The sorted linked list can be partitioned into sorted linked list for the points in $P_1,P_2,\dots ,P_k$ in $O\left(n\right)$ time. The points $p_{t_1},p_{t_2},\dots ,p_{t_k}$ can be found for $P_1,P_2,\dots ,P_k$, respectively in $O\left(n\right)$ time. If the height of the tree is $h$, overall time complexity of the algorithm is $O\left(nh\right)$. Note that the height of the tree is at most the diameter $d$ of the tree (and the height can be $\lceil d∕2\rceil$ if a center vertex of the tree is chosen as the root). Thus the following theorem holds.

Theorem 2

Let $T$ be a tree and let $P$ be a set of points where no two points lie on the same horizontal or vertical line. Then Algorithm $L$ -shaped_Draw_Tree finds an $L$ -shaped point set embedding of $T$ on $P$ in $O\left(nd\right)$ time, where $d$ is the diameter of the tree.

4 $L$-shaped point set embeddings of Halin graphs

In this section we show that any Halin graph of $n$ vertices admits a plane $L$-shaped point set embedding whose vertices are given points in the plane, no two of which lie on the same horizontal or vertical line as in the following theorem.

Theorem 3

Let $G$ be a Halin graph and let $P$ be a set of points where no two points lie on the same horizontal or vertical line. Then $G$ admits an $L$ -shaped point set embedding on $P$ and such an embedding can be found in $O\left(nd\right)$ time where $d$ is the diameter of the core tree.

Proof

Let $G=(V,E)$ be a Halin graph with the core tree $T$. We make $T$ an ordered rooted tree by taking an arbitrary leaf as the root of $T$ and ordering the children of each vertex in a counter clockwise order which reflects the plane embedding of $G$ as shown in Fig. 5(c). Let $P$ be a set of points where no two points lie on the same horizontal or vertical line. We then connect the edges of $T$ by $L$-shaped edges according to the $L$-shaped point set embedding of $T$ mentioned in Theorem 1. One can observe that the resulting $L$-shaped point set embedding is a tree that corresponds to the ordered rooted tree $T$ as illustrated in Fig. 5(d).

We are now going to connect the outer edges of Halin graph. Since the points corresponding to vertices of the outer edges are on the points which are at outer side of each vertical strip, we can easily connect two points by $L$-shaped edges. One can observe that the resulting $L$-shaped point set embedding is a Halin graph as illustrated in Fig. 5(e).

Since we found $L$-shaped point set embedding of a tree in $O\left(nd\right)$ time where $d$ is the diameter of the tree according to Theorem 2, the overall time complexity is $O\left(nd\right)$ where $d$ is the diameter of the core tree.□

Fig. 5 (a) A Halin graph $G$, (b) a point set and (c) an ordered rooted tree $T$ and (d) an $L$-shaped point set embedding of $T$ and (e) an $L$-shaped point set embedding of $G$.

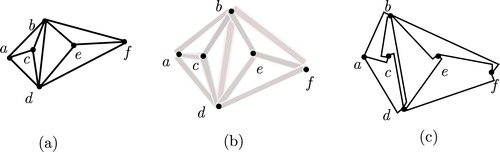
A straight-line point set embedding of a plane graph $G$ on a point set $P$ is a point set embedding of $G$ on $P$ such that each edge of $G$ is drawn as a straight line segment without any bend. It is known that a tree and an outerplanar graph have straight-line point set embeddings [10,11]. If we get a straight-line point set embedding of a plane graph then we can draw the $L$-shaped point set embedding of that graph. We have the following theorem.

Theorem 4

Let $G$ be a plane graph and let $P$ be a set of points. If $G$ has a straight-line point set embedding on $P$ then $G$ admits an $L$ -shaped point set embedding on $P$ .

Proof

Let $G$ be a plane graph and $p_1,p_2,\dots ,p_n$ be the points of $P$. Let $D$ be a straight-line point set embedding of $G$. We convert the straight line segment into a rectangle with $ϵ$ width in $D$ as illustrated in Fig. 6(b). In this area we draw an $L$-shaped edge instead of each straight line segment as illustrated in Fig. 6(c). Hence the resultant embedding is a plane $L$-shaped point set embedding on $P$.

Fig. 6 (a) A graph, (b) the straight line segment is converted into a rectangle with $ϵ$ width in $D$ and (c) $L$-shaped edges instead of each straight line segment in $D$.

By using the algorithm described in the proof of Theorem 4 we get an $L$-shaped point set embedding where the ratio of lengths of the two line segments of an $L$-shaped edge is not pleasant. But we may get useful $L$-shaped point set embeddings of trees and Halin Graphs by using the algorithm described in the proofs of Theorems 1 and 3.

5 Conclusion

In this paper we have introduced $L$-shaped point set embeddings to deal with plane graphs. We have shown that every tree of $n$ vertices admits an $L$-shaped point set embedding on $P$ where $P$ is a point set on a $2D$ plane such that no two points in $P$ lie on a horizontal or on a vertical line and such an embedding can be found in $O\left(nd\right)$ time where $d$ is the diameter of the tree. We also have shown that every Halin graph of $n$ vertices has an $L$-shaped point set embedding on $P$ and such an embedding can also be found in $O\left(nd\right)$ time where $d$ is the diameter of the core tree.

Our research opens following problems.

1.	Provide an algorithm that computes $L$-shaped point set embedding of some larger classes of graphs where maximum degree is five or more.
2.	Decide whether a plane graph $G_{\varphi }$ admits an $L$-shaped drawing.
3.	Decide whether there exists an embedding $G_{\varphi }$ of a planar graph $G$ such that $G_{\varphi }$ admits an $L$-shaped drawing.