Generalized fuzzy b-closed and generalized ⋆-fuzzy b-closed sets in double fuzzy topological spaces

Abstract

The purpose of this paper is to introduce and study a new class of fuzzy sets called (r, s)-generalized fuzzy b-closed sets and (r, s)-generalized ⋆-fuzzy b-closed sets in double fuzzy topological spaces. Furthermore, the relationships between the new concepts are introduced and established with some interesting examples.

Keywords:

• Double fuzzy topology
• (r, s)-generalized fuzzy b-closed sets
• (r, s)-generalized ⋆-fuzzy b-closed sets

Mathematics subject classification:

• 54A40
• 45D05
• 03E72

1 Introduction

A progressive development of fuzzy sets [1] has been made to discover the fuzzy analogues of the crisp sets theory. On the other hand, the idea of intuitionistic fuzzy sets was first introduced by Atanassov [2]. Later on, Çoker [3] presented the notion of intuitionistic fuzzy topology. Samanta and Mondal [4], introduced and characterized the intuitionistic gradation of openness of fuzzy sets which is a generalization of smooth topology and the topology of intuitionistic fuzzy sets. The name “intuitionistic” is discontinued in mathematics and applications. Garcia and Rodabaugh [5] concluded that they work under the name “double”.

In 2009, Omari and Noorani [6] introduced generalized b-closed sets (briefly, gb-closed) in general topology. As a generalization of the results in References 6 and 7, we introduce and study (r, s)-generalized fuzzy b-closed sets in double fuzzy topological spaces, then a new class of fuzzy sets between an (r, s)-fuzzy b-closed sets and an (r, s)-generalized fuzzy b-closed sets namely (r, s)-generalized ⋆-fuzzy b-closed sets is introduced and investigated. Finally, the relationships between (r, s)-generalized fuzzy b-closed and (r, s)-generalized ⋆-fuzzy b-closed sets are introduced and established with some interesting counter examples.

2 Preliminaries

Throughout this paper, X will be a non-empty set, I = [0, 1], I₀ = (0, 1] and I₁ = [0, 1). A fuzzy set λ is quasi-coincident with a fuzzy set µ (denoted by, λqµ) iff there exists x ∈ X such that $\lambda (x)+\mu (x)>1$ and they are not quasi-coincident otherwise (denoted by, $\lambda \overline{q}\mu$). The family of all fuzzy sets on X is denoted by I^X. By $\underset{¯}{0}$ and $\underset{¯}{1}$, we denote the smallest and the greatest fuzzy sets on X. For a fuzzy set λ ∈ I^X, $\underset{¯}{1}-\lambda$ denotes its complement. All other notations are standard notations of fuzzy set theory.

Now, we recall the following definitions which are useful in the sequel.

Definition 2.1

(see [4]) A double fuzzy topology (τ, τ*) on X is a pair of maps τ, τ* : I^X → I, which satisfies the following properties:

Table

(O1)	$\tau (\lambda )\le \underset{¯}{1}-\tau *(\lambda )$ for each λ ∈ I^X.
(O2)	$\tau ({\lambda }_1\wedge {\lambda }_2)\ge \tau ({\lambda }_1)\wedge \tau ({\lambda }_2)$ and $\tau *({\lambda }_1\wedge {\lambda }_2)\le \tau *({\lambda }_1)\vee \tau *({\lambda }_2)$ for each λ1, λ2 ∈ I^X.
(O3)	$\tau ({\vee }_{i\in \Gamma }{\lambda }_i)\ge {\wedge }_{i\in \Gamma }\tau ({\lambda }_i)$ and $\tau *({\vee }_{i\in \Gamma }{\lambda }_i)\le {\vee }_{i\in \Gamma }\tau *({\lambda }_i)$ for each λi ∈ I^X, i ∈ Γ.

The triplet (X, τ, τ*) is called a double fuzzy topological space (briefly, dfts). A fuzzy set λ is called an (r, s)-fuzzy open (briefly, (r, s)-fo) if τ(λ) ≥ r and τ*(λ) ≤ s. A fuzzy set λ is called an (r, s)-fuzzy closed (briefly, (r, s)-fc) set iff $\underset{¯}{1}-\lambda$ is an (r, s)-fo set.

Theorem 2.1

(see [8]) Let (X, τ, τ*) be a dfts. Then double fuzzy closure operator and double fuzzy interior operator of λ ∈ I^X are defined by

$C_{\tau ,\tau *}(\lambda ,r,s)=\wedge \{\mu \in I^X|\lambda \le \mu ,\tau (\underset{¯}{1}-\mu )\ge r,\tau *(\underset{¯}{1}-\mu )\le s\},$$I_{\tau ,\tau *}(\lambda ,r,s)=\vee \{\mu \in I^X|\mu \le \lambda ,\tau (\mu )\ge r,\tau *(\mu )\le s\}.$Where r ∈ I₀ and s ∈ I₁ such that r + s ≤ 1.

Definition 2.2

Let (X, τ, τ*) be a dfts. For each λ ∈ I^X, r ∈ I₀ and s ∈ I₁. A fuzzy set λ is called:

1.	An (r, s)-fuzzy semiopen (see [9]) (briefly, (r, s)-fso) if $\lambda \le C_{\tau ,\tau *}(I_{\tau ,\tau *}(\lambda ,r,s),r,s)$. λ is called an (r, s)-fuzzy semi closed (briefly, (r, s)-fsc) iff $\underset{¯}{1}-\lambda$ is an (r, s)-fso set.

2.	An (r, s)-generalized fuzzy closed (see [10]) (briefly, (r, s)-gfc) if $C_{\tau ,\tau *}(\lambda ,r,s)\le \mu$, λ ≤ µ, τ(µ) ≥ r and τ*(µ) ≤ s. λ is called an (r, s)-generalized fuzzy open (briefly, (r, s)-gfo) iff $\underset{¯}{1}-\lambda$ is (r, s)-gfc set.

Definition 2.3

(see [11,12]) Let (X, τ, τ*) be a dfts. For each λ, µ ∈ I^X and r ∈ I₀, s ∈ I₁. Then, a fuzzy set λ is said to be (r, s)-fuzzy generalized ψρ-closed (briefly, (r, s)-fgψρ-closed) if $\psi C_{\tau ,\tau *}(\lambda ,r,s)\le \mu$ such that λ ≤ µ and µ is (r, s)-fuzzy ρ-open set. λ is called (r, s)-fuzzy generalized ψρ-open (briefly, (r, s)-fgψρ-open) iff $\underset{¯}{1}-\lambda$ is (r, s)-fgψρ-closed set.

3 (r, s)-generalized fuzzy b-closed sets

In this section, we introduce and study some basic properties of a new class of fuzzy sets called an (r, s)-fuzzy b-closed sets and an (r, s)-generalized fuzzy b-closed.

Definition 3.1

Let (X, τ, τ*) be a dfts. For each λ ∈ I^X, r ∈ I₀ and s ∈ I₁. A fuzzy set λ is called:

1.	An (r, s)-fuzzy b-closed (briefly, (r, s)-fbc) if$\lambda \ge (I_{\tau ,\tau *}(C_{\tau ,\tau *}(\lambda ,r,s),r,s))\wedge (C_{\tau ,\tau *}(I_{\tau ,\tau *}(\lambda ,r,s),r,s)).$λ is called an (r, s)-fuzzy b-open (briefly, (r, s)-fbo) iff $\underset{¯}{1}-\lambda$ is (r, s)-fbc set.

2.	An (r, s)-generalized fuzzy b-closed (briefly, (r, s)-gfbc) if $b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \mu$, λ ≤ µ, τ(µ) ≥ r and τ*(µ) ≤ s. λ is called an (r, s)-generalized fuzzy b-open (briefly, (r, s)-gfbo) iff $\underset{¯}{1}-\lambda$ is (r, s)-gfbc set.

Definition 3.2

Let (X, τ, τ*) be a dfts. Then double fuzzy b-closure operator and double fuzzy b-interior operator of λ ∈ I^X are defined by

$b{C}_{\tau ,\tau *}(\lambda ,r,s)=\wedge \{\mu \in I^X|\lambda \le \mu \text{and}\mu \text{is}(r,s)\text{-fbc}\},$$b{I}_{\tau ,\tau *}(\lambda ,r,s)=\vee \{\mu \in I^X|\mu \le \lambda \text{and}\mu \text{is}(r,s)\text{-fbo}\}.$Where r ∈ I₀ and s ∈ I₁ such that r + s ≤ 1.

Remark 3.1

Every (r, s)-fbc set is an (r, s)-gfbc set.

The converse of the above remark may be not true as shown by the following example.

Example 3.1

Let X = {a, b}. Defined µ, α and β by:

$\mu (a)=0.3,\mu (b)=0.4,$$\alpha (a)=0.4,\alpha (b)=0.5,$$\beta (a)=0.3,\beta (b)=0.7,$$\tau (\lambda )=\{\begin{array}{ll}1,\hfill & \text{if}\lambda \in \{\underset{¯}{0},\underset{¯}{1}\},\hfill \\ \frac{1}{2},\hfill & \text{if}\lambda =\mu ,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\tau *(\lambda )=\{\begin{array}{ll}0,\hfill & \text{if}\lambda \in \{\underset{¯}{0},\underset{¯}{1}\},\hfill \\ \frac{1}{2},\hfill & \text{if}\lambda =\mu ,\hfill \\ 1,\hfill & \text{otherwise}.\hfill \end{array}$

Then β is an $\left(\frac{1}{2},\frac{1}{2}\right)$-gfbc set but not an $\left(\frac{1}{2},\frac{1}{2}\right)$-fbc set.

Definition 3.3

Let (X, τ, τ*) be a dfts, λ ∈ I^X, r ∈ I₀ and s ∈ I₁. λ is called an (r, s)-fuzzy b-Q-neighborhood of x_t ∈ P_t(X) if there exists an (r, s)-fbo set µ ∈ I^X such that x_tqµ and µ ≤ λ.

The family of all (r, s)-fuzzy b-Q-neighborhood of x_t denoted by $b\text{-}Q(x_t\text{},r,s)$.

Theorem 3.1

Let (X, τ, τ*) be a dfts. Then for each λ, µ ∈ I^X, r ∈ I₀ and s ∈ I₁, the operator $b{C}_{\tau ,\tau *}$ satisfies the following statements:

Table

(C1)	$b{C}_{\tau ,\tau *}(\underset{¯}{0},r,s)=\underset{¯}{0}$, $b{C}_{\tau ,\tau *}(\underset{¯}{1},r,s)=\underset{¯}{1}$,
(C2)	$\lambda \le b{C}_{\tau ,\tau *}(\lambda ,r,s)$,
(C3)	If λ ≤ µ, then $b{C}_{\tau ,\tau *}(\lambda ,r,s)\le b{C}_{\tau ,\tau *}(\mu ,r,s)$,
(C4)	If λ is an (r, s)-fbc, then $\lambda =b{C}_{\tau ,\tau *}(\lambda ,r,s)$,
(C5)	If µ is an (r, s)-fbo, then µqλ iff $\mu qb{C}_{\tau ,\tau *}(\lambda ,r,s)$,
(C6)	$b{C}_{\tau ,\tau *}(b{C}_{\tau ,\tau *}(\lambda ,r,s),r,s)=b{C}_{\tau ,\tau *}(\lambda ,r,s)$,
(C7)	$b{C}_{\tau ,\tau *}(\lambda ,r,s)\vee b{C}_{\tau ,\tau *}(\mu ,r,s)\le b{C}_{\tau ,\tau *}(\lambda \vee \mu ,r,s)$,
(C8)	$b{C}_{\tau ,\tau *}(\lambda ,r,s)\wedge b{C}_{\tau ,\tau *}(\mu ,r,s)\ge b{C}_{\tau ,\tau *}(\lambda \wedge \mu ,r,s)$,

Proof

(1), (2), (3), and (4) are proved easily.

(5) Let $\mu \overline{q}\lambda$ and µ is an (r, s)-fbo set, then $\lambda \le \underset{¯}{1}-\mu$. But we have, µqλ iff $\mu qb{C}_{\tau ,\tau *}(\lambda ,r,s)$ and$b{C}_{\tau ,\tau *}(\lambda ,r,s)\le b{C}_{\tau ,\tau *}(\underset{¯}{1}-\mu ,r,s)=\underset{¯}{1}-\mu ,$so $\mu \overline{q}b{C}_{\tau ,\tau *}(\lambda ,r,s)$, which is contradiction. Then µqλ iff $\mu qb{C}_{\tau ,\tau *}(\lambda ,r,s)$.

(6) Let x_t be a fuzzy point such that $x_t\nleqq b{C}_{\tau ,\tau *}(\lambda ,r,s)$. Then there is an (r, s)-fuzzy b-Q neighborhood µ of x_t such that $\mu \overline{q}\lambda$. But by (5), we have an (r, s)-fuzzy b-Q-neighborhood µ of x_t such that$\mu \overline{q}b{C}_{\tau ,\tau *}(\lambda ,r,s)$

Also,$x_t\nleqq b{C}_{\tau ,\tau *}(b{C}_{\tau ,\tau *}(\lambda ,r,s),r,s).$

Then$b{C}_{\tau ,\tau *}(b{C}_{\tau ,\tau *}(\lambda ,r,s),r,s)\le b{C}_{\tau ,\tau *}(\lambda ,r,s).$

But we have,$b{C}_{\tau ,\tau *}(b{C}_{\tau ,\tau *}(\lambda ,r,s),r,s)\ge b{C}_{\tau ,\tau *}(\lambda ,r,s).$

Therefore$b{C}_{\tau ,\tau *}(b{C}_{\tau ,\tau *}(\lambda ,r,s),r,s)=b{C}_{\tau ,\tau *}(\lambda ,r,s).$

(7) and (8) are obvious.

Theorem 3.2

Let (X, τ, τ*) be a dfts. Then for each λ, µ ∈ I^X, r ∈ I₀ and s ∈ I₁, the operator $b{I}_{\tau ,\tau *}$ satisfies the following statements:

1.	$b{I}_{\tau ,\tau *}(\underset{¯}{1}-\lambda ,r,s)=\underset{¯}{1}-b{C}_{\tau ,\tau *}(\lambda ,r,s)$, $b{C}_{\tau ,\tau *}(\underset{¯}{1}-\lambda ,r,s)=\underset{¯}{1}-b{I}_{\tau ,\tau *}(\lambda ,r,s),$

2.	$b{I}_{\tau ,\tau *}(\underset{¯}{0},r,s)=\underset{¯}{0},b{I}_{\tau ,\tau *}(\underset{¯}{1},r,s)=\underset{¯}{1}$,

3.	$b{I}_{\tau ,\tau *}(\lambda ,r,s)\le \lambda$,

4.	If λ is an (r, s)-fbo, then $\lambda =b{I}_{\tau ,\tau *}(\lambda ,r,s)$,

5.	If λ ≤ µ, then $b{I}_{\tau ,\tau *}(\lambda ,r,s)\le b{I}_{\tau ,\tau *}(\mu ,r,s)$,

6.	$b{I}_{\tau ,\tau *}(b{I}_{\tau ,\tau *}(\lambda ,r,s),r,s)=b{I}_{\tau ,\tau *}(\lambda ,r,s)$,

7.	$b{I}_{\tau ,\tau *}(\lambda \vee \mu ,r,s)\ge b{I}_{\tau ,\tau *}(\lambda ,r,s)\vee b{I}_{\tau ,\tau *}(\mu ,r,s)$,

8.	$b{I}_{\tau ,\tau *}(\lambda \wedge \mu ,r,s)\le b{I}_{\tau ,\tau *}(\lambda ,r,s)\wedge b{I}_{\tau ,\tau *}(\mu ,r,s)$.

Proof

It is similar to Theorem 3.1.

Theorem 3.3

Let (X, τ, τ*) be a dfts. λ ∈ I^X is (r, s)-gfbo set, r ∈ I₀ and s ∈ I₁ if and only if $\mu \le b{I}_{\tau ,\tau *}(\lambda ,r,s)$ whenever µ ≤ λ, $\tau (\underset{¯}{1}-\mu )\ge r$ and $\tau *(\underset{¯}{1}-\mu )\le s$.

Proof

Suppose that λ is an (r, s)-gfbo set in I^X, and let $\tau (\underset{¯}{1}-\mu )\ge r$ and $\tau *(\underset{¯}{1}-\mu )\le s$ such that µ ≤ λ. By the definition, $\underset{¯}{1}-\lambda$ is an (r, s)-gfbc set in I^X. So,

$b{C}_{\tau ,\tau *}(\underset{¯}{1}-\lambda ,r,s)\le \underset{¯}{1}-\mu$

Also,$\underset{¯}{1}-b{I}_{\tau ,\tau *}(\lambda ,r,s)\le \underset{¯}{1}-\mu .$

And then,$\mu \le b{I}_{\tau ,\tau *}(\lambda ,r,s).$

Conversely, let µ ≤ λ, $\tau (\underset{¯}{1}-\mu )\ge r$ and $\tau *(\underset{¯}{1}-\mu )\le s$, r ∈ I₀ and s ∈ I₁ such that $\mu \le b{I}_{\tau ,\tau *}(\lambda ,r,s)$. Now$\underset{¯}{1}-b{I}_{\tau ,\tau *}(\lambda ,r,s)\le \underset{¯}{1}-\mu ,$

Thus$b{C}_{\tau ,\tau *}(\underset{¯}{1}-\lambda ,r,s)\le \underset{¯}{1}-\mu .$

That is, $\underset{¯}{1}-\lambda$ is an (r, s)-gfbc set, then λ is an (r, s)-gfbo set.

Theorem 3.4

Let (X, τ, τ*) be a dfts, λ ∈ I^X, r ∈ I₀ and s ∈ I₁. If λ is an (r, s)-gfbc set, then

1.	$b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ does not contain any non-zero (r, s)-fc sets.

2.	λ is an (r, s)-fbc iff $b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ is (r, s)-fc.

3.	µ is (r, s)-gfbc set for each set µ ∈ IX such that $\lambda \le \mu \le b{C}_{\tau ,\tau *}(\lambda ,r,s)$.

4.	For each (r, s)-fo set µ ∈ IX such that µ ≤ λ, µ is an (r, s)-gfbc relative to λ if and only if µ is an (r, s)-gfbc in IX.

5.	For each an (r, s)-fbo set µ ∈ IX such that $b{C}_{\tau ,\tau *}(\lambda ,r,s)\overline{q}\mu$ iff $\lambda \overline{q}\mu$.

Proof

(1) Suppose that $\tau (\underset{¯}{1}-\mu )\ge r$ and $\tau *(\underset{¯}{1}-\mu )\le s$, r ∈ I₀ and s ∈ I₁ such that $\mu \le b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ whenever λ ∈ I^X is an (r, s)-gfbc set. Since $\underset{¯}{1}-\mu$ is an (r, s)-fo set,

$\begin{array}{c}\lambda \le (\underset{¯}{1}-\mu )\Rightarrow b{C}_{\tau ,\tau *}(\lambda ,r,s)\le (\underset{¯}{1}-\mu )\\ \Rightarrow \mu \le (\underset{¯}{1}-b{C}_{\tau ,\tau *}(\lambda ,r,s))\\ \Rightarrow \mu \le (\underset{¯}{1}-b{C}_{\tau ,\tau *}(\lambda ,r,s))\wedge (b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda )\\ =\underset{¯}{0}\end{array}$and hence $\mu =\underset{¯}{0}$ which is a contradiction. Then $b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ does not contain any non-zero (r, s)-fc sets.

(2) Let λ be an (r, s)-gfbc set. So, for each r ∈ I₀ and s ∈ I₁ if λ is an (r, s)-fbc set then,$b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda =\underset{¯}{0}$which is an (r, s)-fc set.

Conversely, suppose that $b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ is an (r, s)-fc set. Then by (1), $b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ does not contain any non-zero an (r, s)-fc set. But $b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ is an (r, s)-fc set, then$b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda =\underset{¯}{0}\Rightarrow \lambda =b{C}_{\tau ,\tau *}(\lambda ,r,s).$

So, λ is an (r, s)-fbc set.

(3) Suppose that τ(α) ≥ r and τ*(α) ≤ s where r ∈ I₀ and s ∈ I₁ such that µ ≤ α and let λ be an (r, s)-gfbc set such that λ ≤ α. Then$b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \alpha .$

So,$b{C}_{\tau ,\tau *}(\lambda ,r,s)=b{C}_{\tau ,\tau *}(\mu ,r,s),$

Therefore$b{C}_{\tau ,\tau *}(\mu ,r,s)\le \alpha .$

So, µ is an (r, s)-gfbc set.

(4) Let λ be an (r, s)-gfbc and τ(λ) ≥ r and τ*(λ) ≤ s, where r ∈ I₀ and s ∈ I₁. Then $b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \lambda$. But, µ ≤ λ so,$b{C}_{\tau ,\tau *}(\mu ,r,s)\le b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \lambda .$

Also, since µ is an (r, s)-gfbc relative to λ, then$\lambda \wedge b{C}_{\tau ,\tau *(\lambda )}(\mu ,r,s)=b{C}_{\tau ,\tau *}(\mu ,r,s),$so$b{C}_{\tau ,\tau *}(\mu ,r,s)=b{C}_{\tau ,\tau *(\lambda )}(\mu ,r,s)\le \lambda .$

Now, if µ is an (r, s)-gfbc relative to λ and τ(α) ≥ r and τ*(α) ≤ s where r ∈ I₀ and s ∈ I₁ such that µ ≤ α, then for each an (r, s)-fo set α ∧ λ, $\mu =\mu \wedge \lambda \le \alpha \wedge \lambda$. Hence µ is an (r, s)-gfbc relative to λ,$b{C}_{\tau ,\tau *}(\mu ,r,s)=b{C}_{\tau ,\tau *(\lambda )}(\mu ,r,s)\le (\alpha \wedge \lambda )\le \alpha .$

Therefore, µ is an (r, s)-gfbc in I^X.

Conversely, let µ be an (r, s)-gfbc set in I^X and τ(α) ≥ r and τ*(α) ≤ s whenever α ≤ λ such that µ ≤ α, r ∈ I₀ and s ∈ I₁. Then for each an (r, s)-fo set β ∈ I^X, α = β ∧ λ. But we have, µ is an (r, s)-gfbc set in I^X such that µ ≤ β,$b{C}_{\tau ,\tau *}(\mu ,r,s)\le \beta \Rightarrow b{C}_{\tau ,\tau *(\lambda )}(\mu ,r,s)=b{C}_{\tau ,\tau *}(\mu ,r,s)\wedge \lambda \le \beta \wedge \lambda =\alpha .$

That is, µ is an (r, s)-gfbc relative to λ.

(5) Suppose µ is an (r, s)-fbo and $\lambda \overline{q}\mu$, r ∈ I₀ and s ∈ I₁. Then $\lambda \le (\underset{¯}{1}-\mu )$. Since $(\underset{¯}{1}-\mu )$ is an (r, s)-fbc set of I^X and λ is an (r, s)-gfbc set, then$b{C}_{\tau ,\tau *}(\lambda ,r,s)\overline{q}\mu .$

Conversely, let µ be an (r, s)-fbc set of I^X such that λ ≤ µ, r ∈ I₀ and s ∈ I₁. Then$\lambda \overline{q}(\underset{¯}{1}-\mu ).$

But$b{C}_{\tau ,\tau *}(\lambda ,r,s)\overline{q}(\underset{¯}{1}-\mu )\Rightarrow b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \mu .$

Hence λ is an (r, s)-gfbc.

Proposition 3.1

Let (X, τ, τ*) be a dfts, λ ∈ I^X, r ∈ I₀ and s ∈ I₁.

1.	If λ is an (r, s)-gfbc and an (r, s)-fbo set, then λ is an (r, s)-fbc set.

2.	If λ is an (r, s)-fo and an (r, s)-gfbc, then λ ∧ µ is an (r, s)-gfbc set whenever $\mu \le b{C}_{\tau ,\tau *}(\lambda ,r,s)$.

Proof

(1) Suppose λ is an (r, s)-gfbc and an (r, s)-fbo set such that λ ≤ λ, r ∈ I₀ and s ∈ I₁. Then

$b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \lambda .$

But we have,$\lambda \le b{C}_{\tau ,\tau *}(\lambda ,r,s).$

Then,$\lambda =b{C}_{\tau ,\tau *}(\lambda ,r,s).$

Therefore, λ is an (r, s)-fbc set.

(2) Suppose that λ is an (r, s)-fo and an (r, s)-gfbc set, r ∈ I₀ and s ∈ I₁. Then$\begin{array}{c}b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \lambda \Rightarrow \lambda \text{is an}(r,s)\text{-fbc set}\\ \Rightarrow \lambda \wedge \mu \text{is an}(r,s)\text{-fbc}\\ \Rightarrow \lambda \wedge \mu \text{is an}(r,s)\text{-gfbc}.\end{array}$

4 (r, s)-generalized ⋆-fuzzy b-closed sets

In this section, we introduce and study some properties of a new class of fuzzy sets called an (r, s)-generalized ⋆-fuzzy closed sets and an (r, s)-generalized ⋆-fuzzy b-closed sets

Definition 4.1

Let (X, τ, τ*) be a dfts. For each λ ∈ I^X, r ∈ I₀ and s ∈ I₁. A fuzzy set λ is called:

1.	An (r, s)-generalized ⋆-fuzzy closed (briefly, (r, s)-g ⋆fc) if $C_{\tau ,\tau *}(\lambda ,r,s)\le \mu$ whenever λ ≤ µ and µ is an (r, s)-gfo set in IX. λ is called an (r, s)-generalized ⋆-fuzzy open (briefly, (r, s)-g ⋆fo) iff $\underset{¯}{1}-\lambda$ is (r, s)-g ⋆fc set.

2.	An (r, s)-generalized ⋆-fuzzy b-closed (briefly, (r, s)-g ⋆fbc) if $b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \mu$ whenever λ ≤ µ and µ is an (r, s)-gfo set in IX. λ is called an (r, s)-generalized ⋆-fuzzy b-open (briefly, (r, s)-g ⋆fbo) iff $\underset{¯}{1}-\lambda$ is (r, s)-g ⋆fbc set.

Theorem 4.1

Let (X, τ, τ*) be a dfts. λ ∈ I^X is an (r, s)-g ^⋆fbo set if and only if $\mu \le b{I}_{\tau ,\tau *}(\lambda ,r,s)$ whenever µ is an (r, s)-gfc, r ∈ I₀ and s ∈ I₁.

Proof

Suppose that λ is an (r, s)-g ⋆fbo set in I^X, and let µ is an (r, s)-gfc set such that µ ≤ λ, r ∈ I₀ and s ∈ I₁. So by the definition, we have $\underset{¯}{1}-\lambda$ is an (r, s)-gfo set in I^X and $\underset{¯}{1}-\lambda \le \underset{¯}{1}-\mu$. But $\underset{¯}{1}-\lambda$ is an (r, s)-g ⋆fbc set, then $b{C}_{\tau ,\tau *}(\underset{¯}{1}-\lambda ,r,s)\le \underset{¯}{1}-\mu$. But

$b{C}_{\tau ,\tau *}(\underset{¯}{1}-\lambda ,r,s)=\underset{¯}{1}-b{I}_{\tau ,\tau *}(\lambda ,r,s)\le \underset{¯}{1}-\mu .$

Therefore,$\mu \le b{I}_{\tau ,\tau *}(\lambda ,r,s).$

Conversely, suppose that $\mu \le b{I}_{\tau ,\tau *}(\lambda ,r,s)$ whenever µ ≤ λ and µ is an (r, s)-gfc set, r ∈ I₀ and s ∈ I₁. Now$\underset{¯}{1}-b{I}_{\tau ,\tau *}(\lambda ,r,s)\le \underset{¯}{1}-\mu ,$

Thus$b{C}_{\tau ,\tau *}(\underset{¯}{1}-\lambda ,r,s)\le \underset{¯}{1}-\mu .$

Therefore, $\underset{¯}{1}-\lambda$ is an (r, s)-gfbc set and λ is an (r, s)-gfbo set.

Proposition 4.1

Let (X, τ, τ*) be dfts's. For each λ ∈ I^X, r ∈ I₀ and s ∈ I₁

1.	If a fuzzy set λ is an (r, s)-g ⋆fbc, then $b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ contains no non-zero (r, s)-gfc set.

2.	If a fuzzy set λ is an (r, s)-g ⋆fbc, then $b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ is an (r, s)-g ⋆fbo.

3.	An (r, s)-g ⋆fbc set λ is an (r, s)-fbc iff $b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ is an (r, s)-fbc set.

4.	If a fuzzy set λ is an (r, s)-g ⋆fbc, then $\mu =\underset{¯}{1}$, whenever µ is an (r, s)-gfo set and $b{I}_{\tau ,\tau *}(\lambda ,r,s)\vee (\underset{¯}{1}-\lambda )\le \mu$.

Proof

(1) Suppose that λ is an (r, s)-g ⋆fbc set and µ is an (r, s)-gfc set of I^X, r ∈ I₀ and s ∈ I₁ such that

$\mu \le b{C}_{\tau ,\tau *}(\lambda ,r,s)$

And$\lambda \le \underset{¯}{1}-\mu .$

But λ is an (r, s)-g ⋆fbc set and $\underset{¯}{1}-\mu$ is an (r, s)-gfo set, then$b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \underset{¯}{1}-\mu \Rightarrow \mu \le b{C}_{\tau ,\tau *}(\lambda ,r,s)\wedge (\underset{¯}{1}-b{C}_{\tau ,\tau *}(\lambda ,r,s))=\underset{¯}{0}.$

Therefore $b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ contains no non-zero (r, s)-gfc set.

(2) Let λ be an (r, s)-g ⋆fbc set, r ∈ I₀ and s ∈ I₁. Then by (1) we have, $b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ contains no non-zero (r, s)-gfc set. So, $b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ is an (r, s)-g ⋆fbo set.

(3) Let λ be an (r, s)-g ⋆fbc set. If λ is an (r, s)-fbc, r ∈ I₀ and s ∈ I₁, then$b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda =\underset{¯}{0}.$

Conversely, let $b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ is an (r, s)-fbc set in I^X and λ is an (r, s)-g ⋆fbc, r ∈ I₀ and s ∈ I₁, then by (1) we have, $b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda$ contains no non-zero (r, s)-gfc set. Then,$b{C}_{\tau ,\tau *}(\lambda ,r,s)-\lambda =\underset{¯}{0},$that is$b{C}_{\tau ,\tau *}(\lambda ,r,s)=\lambda .$

Hence λ is an (r, s)-fbc set.

(4) Let µ be an (r, s)-gfc set and $b{I}_{\tau ,\tau *}(\lambda ,r,s)\vee (\underset{¯}{1}-\lambda )\le \mu$, r ∈ I₀ and s ∈ I₁. Hence$\underset{¯}{1}-\mu \le b{C}_{\tau ,\tau *}(\underset{¯}{1}-\lambda ,r,s)\wedge \lambda =b{C}_{\tau ,\tau *}(\underset{¯}{1}-\lambda ,r,s)-(\underset{¯}{1}-\lambda ).$

But $(\underset{¯}{1}-\mu )$ is an (r, s)-gfc and $\underset{¯}{1}-\lambda$ is an (r, s)-g ⋆fbc by (1), $\underset{¯}{1}-\mu =\underset{¯}{0}$ and hence $\mu =\underset{¯}{1}$.

Proposition 4.2

Let (X, τ, τ*) be dfts's. For each λ and µ ∈ I^X, r ∈ I₀ and s ∈ I₁.

1.	If λ and µ are (r, s)-g ⋆fbc, then λ∧µ is an (r, s)-g ⋆fbc.

2.	If λ is an (r, s)-g ⋆fbc and τ(µ) ≥ r, τ*(µ) ≤ s, then λ ∧ µ is an (r, s)-g ⋆fbc.

Proof

(1) Suppose that λ and µ are (r, s)-g ⋆fbc sets in I^X such that λ ∧ µ ≤ ν for each an (r, s)-gfo set ν ∈ I^X, r ∈ I₀ and s ∈ I₁. Since λ is an (r, s)-g ⋆fbc,

$b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \nu$for each an (r, s)-gfo set ν ∈ I^X and λ ≤ ν. Also, µ is an (r, s)-g ⋆fbc,$b{C}_{\tau ,\tau *}(\mu ,r,s)\le \nu$for each an (r, s)-gfo set ν ∈ I^X and µ ≤ ν. Then we have,$b{C}_{\tau ,\tau *}(\lambda ,r,s)\wedge b{C}_{\tau ,\tau *}(\mu ,r,s)\le \nu ,$whenever λ ∧ µ ≤ ν, Therefore, λ ∧ µ is an (r, s)-g ⋆fbc.

(2) Since every an (r, s)-fc set is an (r, s)-g ⋆fbc and from (1) we get the proof.

Proposition 4.3

Let (X, τ, τ*) be dfts's. For each λ and µ ∈ I^X, r ∈ I₀ and s ∈ I₁.

1.	If λ is both an (r, s)-gfo and an (r, s)-g ⋆fbc, then λ is an (r, s)-fbc set.

2.	If λ is an (r, s)-g ⋆fbc and $\lambda \le \mu \le b{C}_{\tau ,\tau *}(\lambda ,r,s)$, then µ is an (r, s)-g ⋆fbc.

Proof

(1) Suppose that λ is an (r, s)-gfo and an (r, s)-g ⋆fbc in I^X such that $b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \mu$, r ∈ I₀ and s ∈ I₁. But

$\lambda \le b{C}_{\tau ,\tau *}(\lambda ,r,s).$

Therefore$\lambda =b{C}_{\tau ,\tau *}(\lambda ,r,s).$

Hence λ is an (r, s)-fbc set.

(2) Suppose that λ is an (r, s)-g ⋆fbc and ν is an (r, s)-gfo set in I^X such that µ ≤ ν for each µ ∈ I^X, r ∈ I₀ and s ∈ I₁. So λ ≤ ν. But we have, λ is an (r, s)-g ⋆fbc, then$b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \nu .$

Now$b{C}_{\tau ,\tau *}(\mu ,r,s)\le b{C}_{\tau ,\tau *}(b{C}_{\tau ,\tau *}(\lambda ,r,s),r,s)=b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \nu .$

Therefore µ is an (r, s)-g ⋆fbc set.

Theorem 4.2

Let $(X,{\tau }_1\text{},{\tau }_1^{*})$ and $(Y,{\tau }_2\text{},{\tau }_2^{*})$ be dfts's. If $\lambda \le {\underset{¯}{1}}_Y\le {\underset{¯}{1}}_X$ such that λ is an (r, s)-g ⋆fbc in I^X, r ∈ I₀ and s ∈ I₁, then λ is an (r, s)-g ⋆fbc relative to Y.

Proof

Suppose that $(X,{\tau }_1\text{},{\tau }_1^{*})$ and $(Y,{\tau }_2\text{},{\tau }_2^{*})$ are dfts's such that $\lambda \le {\underset{¯}{1}}_Y\le {\underset{¯}{1}}_X$, r ∈ I₀, s ∈ I₁ and λ is an (r, s)-g ⋆fbc in I^X. Now, let $\lambda \le {\underset{¯}{1}}_Y\wedge \mu$ such that µ is an (r, s)-gfo set in I^X. But we have, λ is an (r, s)-g ^⋆fbc in I^X,

$\lambda \le \mu \Rightarrow b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \mu .$

So that${\underset{¯}{1}}_Y\wedge b{C}_{\tau ,\tau *}(\lambda ,r,s)\le {\underset{¯}{1}}_Y\wedge \mu .$

Hence λ is an (r, s)-g ⋆fbc relative to Y.

Theorem 4.3

Let $(X,{\tau }_1\text{},{\tau }_1^{*})$ be adfts. For each λ and µ ∈ I^X, r ∈ I₀ and s ∈ I₁ with µ ≤ λ. If µ is an (r, s)-g ⋆fbc relative to λ such that λ is both an (r, s)-gfo and (r, s)-g ⋆fbc of I^X, then µ is an (r, s)-g ⋆fbc relative to X.

Proof

Suppose that µ is an (r, s)-g ⋆fbc and τ(ν) ≥ r and τ*(ν) ≤ s such that µ ≤ ν, r ∈ I₀, s ∈ I₁. But we have, $\mu \le \lambda \le \underset{¯}{1}$, therefore µ ≤ λ and µ ≤ ν. So

$\mu \le \lambda \wedge \nu .$

Also we have, µ is an (r, s)-g ⋆fbc relative to λ,$\lambda \wedge b{C}_{\tau ,\tau *}(\mu ,r,s)\le \lambda \wedge \nu \Rightarrow \lambda \wedge b{C}_{\tau ,\tau *}(\mu ,r,s)\le \nu .$

Thus$\begin{array}{l}(\lambda \wedge b{C}_{\tau ,\tau *}(\mu ,r,s))\vee (\underset{¯}{1}-b{C}_{\tau ,\tau *}(\mu ,r,s))\le \nu \vee (\underset{¯}{1}-b{C}_{\tau ,\tau *}(\mu ,r,s)).\\ \Rightarrow \lambda \vee (\underset{¯}{1}-b{C}_{\tau ,\tau *}(\mu ,r,s))\le \nu \vee (\underset{¯}{1}-b{C}_{\tau ,\tau *}(\mu ,r,s)).\end{array}$

Since λ is an (r, s)-g ⋆fbc, then$b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \nu \vee (\underset{¯}{1}-\mu ).$

Also,$\mu \le \lambda \Rightarrow b{C}_{\tau ,\tau *}(\mu ,r,s)\le b{C}_{\tau ,\tau *}(\lambda ,r,s).$

Thus$b{C}_{\tau ,\tau *}(\mu ,r,s)\le b{C}_{\tau ,\tau *}(\lambda ,r,s)\le \nu \vee (\underset{¯}{1}-b{C}_{\tau ,\tau *}(\mu ,r,s)).$

Therefore $b{C}_{\tau ,\tau *}(\mu ,r,s)\le \nu$, but $b{C}_{\tau ,\tau *}(\mu ,r,s)$ is not contained in $(\underset{¯}{1}-b{C}_{\tau ,\tau *}(\mu ,r,s))$. That is, µ is an (r, s)-g ⋆fbc relative to X.

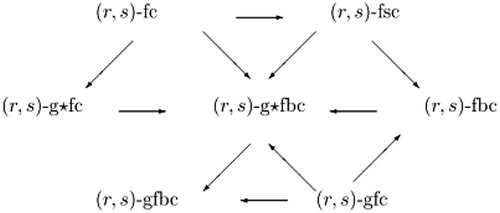
5 Interrelations

The following implication illustrates the relationships between different fuzzy sets:

None of these implications is reversible where A → B represents A implies B, as shown by the following examples. But at this stage we do not have information regarding the relationship between an (r, s)-gfbc and (r, s)-g ⋆fc sets.

Example 5.1

(1) Let $X=\{a,b,c\}$ and let µ and α are fuzzy sets defined by:

$\mu (a)=1.0,\mu (b)=0.5,\mu (c)=0.0,$$\alpha (a)=0.0,\alpha (b)=0.4,\alpha (c)=1.0.$

Define (τ, τ*) on X as follows:$\tau (\lambda )=\{\begin{array}{ll}1,\hfill & \text{if}\lambda \in \{\underset{¯}{0},\underset{¯}{1}\},\hfill \\ \frac{1}{2},\hfill & \text{if}\lambda =\mu ,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\tau *(\lambda )=\{\begin{array}{ll}0,\hfill & \text{if}\lambda \in \{\underset{¯}{0},\underset{¯}{1}\},\hfill \\ \frac{1}{2},\hfill & \text{if}\lambda =\mu ,\hfill \\ 1,\hfill & \text{otherwise}.\hfill \end{array}$

Then α is an $\left(\frac{1}{2},\frac{1}{2}\right)$-gfbc set, but not an $\left(\frac{1}{2},\frac{1}{2}\right)$-g ⋆fbc set.

(2) Take X = {a, b} in (1) and define µ, α and β by:$\mu (a)=0.6,\mu (b)=0.6,$$\alpha (a)=0.3,\alpha (b)=0.2,$$\beta (a)=0.4,\beta (b)=0.5.$

Then β is an $\left(\frac{1}{2},\frac{1}{2}\right)$-g ⋆fbc set, but not an $\left(\frac{1}{2},\frac{1}{2}\right)$-fbc set.

(3) Let $X=\{a,b,c\}$. Define µ, ν and γ by:$\mu (a)=1.0,\mu (b)=0.5,\mu (c)=0.3,$$\nu (a)=1.0,\nu (b)=0.6,\nu (c)=0.0,$$\gamma (a)=0.0,\gamma (b)=0.6,\gamma (c)=0.0.$

Define (τ, τ*) as in (1). Then ν is an $\left(\frac{1}{2},\frac{1}{2}\right)$-g ⋆fbc set but not an $\left(\frac{1}{2},\frac{1}{2}\right)$-fc set and not an $\left(\frac{1}{2},\frac{1}{2}\right)$-gfc. And γ is an $\left(\frac{1}{2},\frac{1}{2}\right)$-g ⋆fbc set, but not an $\left(\frac{1}{2},\frac{1}{2}\right)$-fsc set.

(4) Take (3) and defined µ and ν by:$\mu (a)=1.0,\mu (b)=1.0,\mu (c)=0.6,$$\nu (a)=0.3,\nu (b)=0.5,\nu (c)=0.5.$

Define (τ, τ*) as in (1). Then ν is an $\left(\frac{1}{2},\frac{1}{2}\right)$-g ⋆fbc set, but not an $\left(\frac{1}{2},\frac{1}{2}\right)$-g ⋆fc set.

(5) See Example 3.1. Clearly β is an $\left(\frac{1}{2},\frac{1}{2}\right)$-gfbc set, but not an $\left(\frac{1}{2},\frac{1}{2}\right)$-gfc set.

(6) Let X = {a, b}. Define µ, ν and γ as follows:$\mu (a)=0.7,\mu (b)=0.6,$$\nu (a)=0.3,\nu (b)=0.2,$$\gamma (a)=0.4,\gamma (b)=0.5.$

Define (τ, τ*) as in (1). Then ν is an $\left(\frac{1}{2},\frac{1}{2}\right)$-fbc set but not an $\left(\frac{1}{2},\frac{1}{2}\right)$-fsc set, also not an $\left(\frac{1}{2},\frac{1}{2}\right)$-gfc.

(7) Let $X=\{a,b,c\}$ and let µ and α as fuzzy sets defined by:$\mu (a)=0.9,\mu (b)=0.8,\mu (c)=0.3,$$\alpha (a)=0.1,\alpha (b)=0.8,\alpha (c)=0.3.$

Define (τ, τ*) on X by:$\tau (\lambda )=\{\begin{array}{ll}1,\hfill & \text{if}\lambda \in \{\underset{¯}{0},\underset{¯}{1}\},\hfill \\ 0.6,\hfill & \text{if}\lambda =\mu ,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\tau *(\lambda )=\{\begin{array}{ll}0,\hfill & \text{if}\lambda \in \{\underset{¯}{0},\underset{¯}{1}\},\hfill \\ 0.3,\hfill & \text{if}\lambda =\mu ,\hfill \\ 1,\hfill & \text{otherwise}.\hfill \end{array}$

Then α is an $(0.6,0.3)$-fsc set, but not an $(0.6,0.3)$-fc set.

(8) Let X = {a, b} and let µ and α as fuzzy sets defined by:$\mu (a)=0.9,\mu (b)=0.4,$$\alpha (a)=0.1,\alpha (b)=0.8.$

Define (τ, τ*) on X by:$\tau (\lambda )=\{\begin{array}{ll}1,\hfill & \text{if}\lambda \in \{\underset{¯}{0},\underset{¯}{1}\},\hfill \\ \frac{1}{2},\hfill & \text{if}\lambda =\mu ,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\tau *(\lambda )=\{\begin{array}{ll}0,\hfill & \text{if}\lambda \in \{\underset{¯}{0},\underset{¯}{1}\},\hfill \\ \frac{1}{2},\hfill & \text{if}\lambda =\mu ,\hfill \\ 1,\hfill & \text{otherwise}.\hfill \end{array}$

Then µ is an $\left(\frac{1}{2},\frac{1}{2}\right)$-g ⋆fc set, but not an $\left(\frac{1}{2},\frac{1}{2}\right)$-fc set.

Acknowledgments

The authors would like to acknowledge the following: UKM Grant DIP-2014-034 and Ministry of Education, Malaysia grant FRGS/1/2014/ST06/UKM/01/1 for financial support.