Singularities of the solutions for the elasticity system in a non homogeneous three-dimensional domain

Abstract

In this paper we consider the linear Lamé equations in a non homogeneous three-dimensional domain Q composed of two homogeneous bodies Q₊ and Q₋ with the boundary condition: contact without friction-Dirichlet. We first establish the existence and uniqueness results for weak solutions. Then using cylindrical coordinates and assuming that the neighborhood of the edge A is sufficiently small, we give the transcendental equations governing the singular behavior in the spatial case. In the end, applying the results of Merouani (1996), we obtain an explicit description of the singularities for the variational solution of the boundary value problem in the homogeneous case, i.e. the two bodies have the same elasticity coefficients.

Keywords:

• Behavior
• Edge
• Elasticity
• Singularity
• Sobolev spaces
• Transcendental function

1 Introduction and notations

In many elasticity problems, the numerical evaluation of the solutions requires the knowledge of the behavior of the components for various boundary conditions in the neighborhood of the singular points on the surface of the considered body. It permits the approximation of a solution in an appropriate manner and the construction of an approximate process for its determination ( Aksentian, 1967; Merouani, 1996; Grisvard, 1986). In Aksentian (1967) the author solved the Laplace, Poisson and elliptic equations in the regions known to be as non regular boundaries. Grisvard (1986) has established in the homogeneous domain of , (n = 2 or 3) the character of non smooth solution to neighborhoods of a bridge in a polyhedron for various boundary conditions. The case of a nonhomogeneous polygon was already considered in Benseridi and Dilmi (2005). The regularity of the solutions of transmission problem for the Laplace operator in was studied in Lemrabet (1978). More recently, the authors in Benseridi and Dilmi (2010) have proved the existence and uniqueness, as well as the regularity of the solution of a boundary value problem with mixed conditions in a neighborhood of an edge in the general framework of weighted Sobolev spaces using the Fourier complex transform with respect to the first variable in a dihedral. The Singularities and regularity of weak solutions for the two-dimensional Lamé equations on domains with angular corners have established in Rössle (2000). Costabel et al. (2001), we have presented a method for the computation of singularity exponents in linear elasticity, which is especially useful in the anisotropic case. The method is based on the construction of a matrix of low dimension depending on a complex variable, whose determinant is 0 for a discrete set of values of this variable. These values are the exponents of singularities.

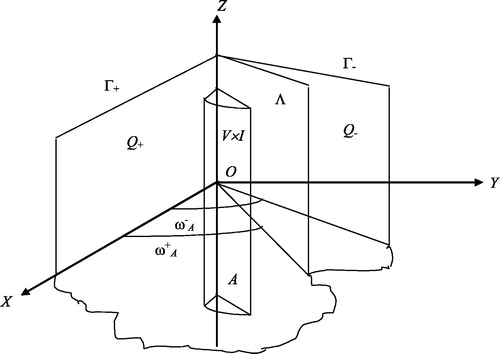
The goal of the present paper is to obtain the singularity and regularity of the solutions of transmission problem related to the Lamé system with boundary condition contact without friction-Dirichlet in a three-dimensional domain Q. More specifically and for the ease of the reader, we give notations that specify our domain: let Ω a bounded sector in divided in two sectors Ω₊ and Ω₋. We suppose that the lateral surface Γ₋ forms an arbitrary angle to the surface Γ₊. Let a domain of constituted by two bodies and by an interface . The generator of this surface is inclined at an angle to the surface of the first body. To express the behavior of the solution of the boundary value problem far away from the vertex see (Grisvard, 1986), we fix an interval I of the opened edge A and where the closing is internal to A. In addition, we fix a neighborhood V of the origin O in the intersection of Q with the plane (xoy) such that does not contain any vertex of Q (see Fig. 1).

Figure 1 Example of 3D domain.

For any function u defined on Q, we designate by u₊ (resp. u₋) its restriction on Q₊ (resp. Q₋). L designates the elasticity system:(1.1) where λ₊, μ₊ are the elasticity coefficients with λ₊ > 0 and (λ₊ + μ₊) ≥ 0. The stress tensor and the displacement vector are related via Hooke’s law:(1.2) where is the symmetric deformation velocity tensor and δ_ij is the symbol of Kroneeker.

Here, the vector η(resp.τ) denotes the normal (resp. the tangent) on toward the interior of Q₊.

The plan of this paper is as follows: In Section 2, we prove the existence and uniqueness results for the weak solution of the Lamé system in a 3D bounded domain Q with boundary condition: contact without friction-Dirichlet. Using the separation variables techniques, we show that the research of singular solutions to the neighborhood of the edge A in the spatial case. In Section 3, we give the transcendental equations governing the singular behavior. The explicit calculus of the singular functions and the singular development of the weak solutions for the homogeneous case has been obtained in Section 4. We end this paper by conclusion and perspectives.

2 Formulation of the problem

For a given (f₊, f₋) ∈ L²(Q₊)³ × L²(Q₋)³, we consider the following problem(2.1)

Theorem 2.1

For a given f₊ in L²(Q₊)³, there exists a unique solution u = (u₊, u₋) in H¹(Q₊)³ × H¹(Q₋)³ of the problem (2.1)(2.1) .

Proof

We denote by V the spaceUsing the Green formula, we get the following variational formulation of problem (2.1)(2.1) whereUsing the Korn inequality and Lax–Milgram theorem we establish the existence and the uniqueness of the solution u to the problem (2.1)(2.1) in H¹(Q₊)³ × H¹(Q₋)³.□

While using the cylindrical coordinates, putting r = e^−t and to express the behavior of the solution of the boundary value problem far away from the vertex, noting that the neighborhood of A is sufficiently small so that terms containing the factor e^−t may be neglected, we obtain the following asymptotic problem(2.2) The quantities u_+r, u_+θ and u_+z are the displacement components in the cylindrical coordinates, and is the Poisson’s ratio for the material of the body Q₊.

Remark 2.1

From the equations of the problem (2.2)(2.2) , we can see that the problem (2.1)(2.1) can be divided into two parts: The first is a plane deformation to which correspond the two first equations, and the second is a normal plane deformation, expressed by the third equations of (2.2)(2.2) .

We look for the solutions of the two problems under the form(2.3) where α is a complex number.

The asymptotic problem (2.2)(2.2) becomes an ordinary differential system which depends analytically on the complex parameter α (the same system of Parton, 1983).(2.4) The general solution of the problem (2.4)(2.4) is given by

For α ∉ {0, + 1}(2.5) For α = 0(2.6) For α = 1(2.7) For α =  − 1(2.8) To define the constants to 4 and j = 1, 2, we use the boundary conditions to the limits defined in Section 2.

The expressions of the components of the stress tensor, in the cylindrical coordinates are given by(2.9) where, τ_+rθ and σ_+θ, are the tangential stress tensor and the normal stress tensor respectively.

The corresponding homogeneous boundary conditions given above, become(2.10)

Remark 2.2

According to the boundary conditions (2.10)(2.10) , we get the following interpretation: on the surface Γ₊, we have contact without friction and the displacements on Γ₋ are vanished, while we have the continuity of the boundary value on the intersection surface .

3 Transcendental equations governing the singular behavior

We determine G, the set of the values α = α(ν₊), such that the problem (2.1)(2.1) has non trivial solutions u = (u_+r, u_+θ, u_+z). We use the following result of Grisvard (1986):

Result 3.1

Every variational solutions u ∈ H¹(Q)³ corresponding to regular data belongs to H^s(V × I)³ for all s < ρ, where

Proposition 3.1

The problem (2.1)(2.1) , determines u which is not vanished when α ∉ {0, +1} is a solution of the system of the transcendental equations Problem of plane deformation.(3.1) whereProblem of normal plane deformation.(3.2)

Proposition 3.2

The problem (2.1)(2.1) , determines u which is not vanished when α = +1 is a solution of the system of the transcendental equations Problem of plane deformation.(3.3) Problem of normal plane deformation.(3.4)

Proof

Using the boundary conditions (2.10)(2.10) , we get a homogeneous system of equations. The structure of these equations allows us to define the homogeneous conditions for which the equations in the previous system admit non trivial solutions as well as the shape of these solutions. The condition of the vanishing of the system’s determinant gives the transcendental equations for the problem (2.1)(2.1) .□

3.1 Study of the transcendental equations

In the most usual contact case between two bodies, for and , the investigation of the singularity of the solution in the neighborhood for a corner gives the transcendental equations (α ∉ {0, +1})Problem of plane deformation.(3.5) Problem of normal plane deformation.(3.6)

4 Singularity solutions of the homogeneous elasticity system

We give an explicit description of the singularities of variational solution of boundary value problems in the homogeneous case, that means, the two bodies Q₊ and Q₋ have the same elasticity coefficients (μ, ν).

For this, we note: and μ = μ₊ = μ₋, where ω represents the solid angle of the surface Γ.

Proposition 4.1

The transcendental equations of the Proposition 3.1, take the following forms:(4.1)

4.1 Singular solutions of the problem (2.1)(2.1)

It is well known for the problems of the type (2.1)(2.1) that the singular solutions are of the form: r^αΦ_α(θ) if α is a simple root and if α is a double root of the transcendental equation (4.1)(4.1) , where Φ_α ∈ (C^∞)³ on ]0, ω[.

The singular solutions of the problem (2.1)(2.1) are given in the following proposition

Proposition 4.2

Let α_l denote the zeros of the transcendental equation (4.1)(4.1) , then the singular solutions of the problem (2.1)(2.1) are given by :

a-	ω ∈ ]0, π[∪]π, 2π[(4.2)
b-	ω = 2π(4.3) (4.4)

Proof

To avoid long computations, we have determined the singular solutions only for the non fissured domain (ω∈]0, π[∪]π , 2π[):

Let α_l denote the zeros of Eq. (4.1)(4.1) in the strip: . By leting θ = 0 in the condition (2.10)(2.10) of the plane problem, we get:(4.5) Finally the boundary conditions for θ = ω give the following system:(4.6) This system can be resolved if its determinant is vanished, it gives the first characteristic equation of (4.1)(4.1) corresponding to the plane problem. Therefore, the solutions of the system (4.6)(4.6) give the two first equations of (4.2)(4.2) .

In the same way using the boundary conditions for the normal plane problem, we obtain the third component of the singular solution. This completes the proof.□

We are now able to address the following subsection concerning:

4.2 Singular development of the weak solutions for (2.1)(2.1)

In our study, we suppose that the solution u ∈ H¹(Q)³. We are interested in the behavior of the solutions of the problem (2.1)(2.1) in an open neighborhood Π = V × I of the edge A. The solution u is a linear combination of the regular part u_R ∈ H²(Q)³ and of r^αΦ_α(θ), wherethe Φ_α(θ) ∈ (C^∞)³ are the solutions of the homogeneous problems associated to the problem (2.1)(2.1) .

Theorem 4.1

Grisvard, 1986

Let be a solution to the problem (2.1)(2.1) , with . Then there exist numbers γ_l and ξ_l such that(4.7) provided that Re α_l is not equal to: , for every and 1 ≤ p ≤ +∞.

Remark 4.1

1-	The αl are the solutions of the transcendental equations (Proposition 4.1).
2-	The proof of the Theorem 4.1 is similar to the one in Grisvard (1986).
3-	The usual regularity result is not true in the neighborhood of an edge A if none of the eigenvalues corresponding to Re αl does not belong to the interval .

It is interesting to consider the case of the crack, for that we have

Property 4.1

Let ω = 2π, then the variational solution u of the problem (2.1)(2.1) belongs to for . In addition, we have

where .

Proof

For ω = 2π, Eq. (4.1)(4.1) becomesIt is immediate to verify that the roots of this system are the numbersThere are no roots in the strip , and this ensures the regularity of u in for .

On the other hand all the roots α_k are multiplicity equal to 1, obviously the only root in ]0, 1[ are the two numbers: and , where the first singular functions:In addition the terms γ_l(r^αΦ_α(θ)) and corresponding to the integer α_k > 1 are polynomials, so they are superfluous in the development (4.7)(4.7) , we can simplify and write the following form:provided that (hence also ) , (i.e.): .□

Remark 4.2

It is immediate to check that for p ≤ 2 dice:

5 Conclusion and perspectives

In this paper we prove the existence, the uniqueness and the regularity results for the weak solution of Lamé equations in a non homogeneous three-dimensional domain Q with boundary condition: contact without friction-Dirichlet. In the non homogeneous case, it is not easy to solve the transcendental equation (3.1)(3.1) , this does not permit us to find the singular solutions, by in the case where the two bodies Q₊ and Q₋ have the same elasticity coefficients (μ, ν), the singular behavior of the solutions is governed by transcendental equations similar to those found by Grisvard (1986) and Merouani (1996)". In a forthcoming paper we propose to study the case of a discontinuity in the interface and this can be reduced to the problem (2.1)(2.1) by using techniques of localization, change of variables and trace theorems.