Quantum communication in the presence of noise local environments

Abstract

We investigate the entanglement dynamics of maximum and partial entangled two-qubit states, where each qubit interacts locally with its own noise environment. In the presence of local non-correlated noise, the entangled system loses its entangled properties faster than that depicted for correlated noise. The capacity of the output channel decays gradually and smoothly in the presence of non-correlated noise and hastily for the correlated one. We show that the local non-correlated noise can improve the capacity of the output channel. The possibility of using the output state to perform quantum teleportation is discussed and the effect of the noise parameter on the fidelity of the teleported state is investigated.

Keywords:

• Entanglement
• Local noise
• Capacity
• Teleportation

1 Introduction

A fundamental resource in the development of quantum information tasks is the phenomenon of quantum entanglement. The recent progresses of quantum information theory prove that entanglement has some important practical applications, where it can be used as a resource for communications via quantum teleportation (Bennett et al., 1993; Bouwmeester, 1997; Boschi et al., 1998), quantum coding (Bennett and Wiesner, 1992; Metwally, 2012), and cloning (Bennett et al., 1992; Wootters and Zurek, 1982). Entanglement also can be viewed as a source of quantum computation (Deutsch (1989)) and quantum cryptography (Lo et al., 1998).

Quantum teleportation is an important process that could be used to transmit quantum information between two separate locations. To achieve this process one needs entangled pairs which represent the quantum channel between the sender and the receiver, local operations and measurements. Therefore, quantum channel can be considered as a physical medium that enables the transfer of quantum information from a sender to a receiver. The general phenomenon of noise, which is present to some extent in all information systems, is defined as the undesirable transformations suffered by a quantum system during the transfer from the sender to the receiver. The actual rate of the transmitted information through a quantum channel is lowered by the presence of the noise (Metwally, 2010, 2011).

Quantum teleportation in a noise environment is studied by Scheel et al. (2001) and Banaszek (2001)" where the fidelity of quantum teleportation using non-maximally entangled states is investigated. Also Ishizaka (2001) studied the quantum teleportation in the presence of noisy channel. Teleportation using Werner states (Werner, 1989) is studied by Lee and Kim (Lee et al., 2000). On the other hand, it was proved by Badziag et al. (2000) that local environment can enhance the fidelity of quantum teleportation. Investigating, the quantum teleportation in the presence of noise operation is carried out in (Ahmed et al., 2012 and Metwally and Wahiddin, 2007).

In this contribution we discuss the problem of teleportation using the generalized Werner state as quantum channels (Englert and Metwally, 2000) in the presence of different types of local noise. Assume that we have a source that supplies two users Alice and Bob with entangled qubits. Each qubit interacts locally with a noise environment. In Section 2, we investigate the dynamics of the generalized Werner states in the presence of local noise environments. Section 3 is devoted to investigate the Peres–Horodecki criterion of separability (Peres, 1996; Horodecki et al., 1996) and quantifying the survival of entanglement in the output states. The capacity of the output state is discussed in Section 4. The possibility of using the output states to perform quantum teleportation is considered in Section 5. Finally we conclude the results in Section 6.

2 The model

Assume that a source supplies two users Alice and Bob with entangled two qubit state of the generalized Werner state (Englert and Metwally, 2000) to achieve any quantum information task. This class of states is described by zero Bloch vectors and arbitrary cross dyadic as(1) where σ_i and τ_i are the Pauli matrices for Alice and Bob’s qubits, respectively, i = x,y and z and I is the identity matrix. The numbers c_j,j = 1,2,3 are called the characteristic values of the cross dyadic where ∣c₁∣ ≥ ∣c₂∣ ≥  ∣c₃∣ ≥ 0. Each qubit interacts locally with its own noise environment. These noises could be identical and their effect on the two different qubits could be correlated or non-correlated. These types of noise can be described by,(2) The dynamics of the generalized Werner state (1)(1) in the presence of local identical correlated noise is given by(3) In the computational basis 0 and 1, the density operator (3)(3) can be written as(4) where the coefficients α_i, i = 1, … 8 are given by(5) However, if we assume that the state (1)(1) interacts locally with identical non-correlated noise, then the output state is given by,(6) In the computational basis, the density operator (6)(6) takes the form(7) where the coefficients γ_i are,(8) Since, we have obtained the output density operators, then one can investigate some different properties of the output entangled state. In the next section, we shed some light on the effect of different types of noise channels on the entangled properties of the output channels. The amount of survived entanglement is quantified. Also, we quantify the capacity of the output channel.

3 Separability and entanglement

Due to the effect of the noise, the output entangled channels lose their quantum correlations and turn into separable channels. To investigate the dynamics of this behavior, we use the Peres–Horodecki’s criterion for separability (Peres, 1996; Horodecki et al., 1996), as known by positive partial transpose criterion (PPT). This criterion states that: a two-qubit density operator, ρ_ab is separable if the partial transpose of the density operator is non-negative, i.e., all the eigenvalues of should be positive. In this context, the density operator (4)(4) is entangled if it violates the Peres–Horodeck’ criterion (PPT), namely,(9) Also the state (7)(7) is entangled if it violates the PPT criterion which means(10) In Fig. 1a, the dynamics of the PPT criterion for different classes of initial states: maximum (MES) and partial (PES) entangled states is plotted. It is assumed that both qubits are interacts with local noise environments. It is clear that, as the channel parameter q increases the output channel of a system prepared initially in MES turns into a separable state for q = 1. However, starting from PES the output entangled state turns into a separable state for smaller values of channel parameter q.

Figure 1 The PPT criterion for different initial entangled states of Werner type against the noise parameter q. The solid curve represents PPT for a system prepared initially in MES with c₁ = c₂ = c₃ = −1. The dot, dash, and dash dot curves for systems prepared initially in PES with c₁ = −0.5,c₂ = c₃ = 1,c₁ = 0,c₂ = c₃ = 1, and c₁ = c₂ = 0.9, c₃ = 0.7 respectively. For(a) correlated noise (b) non correlated noise.

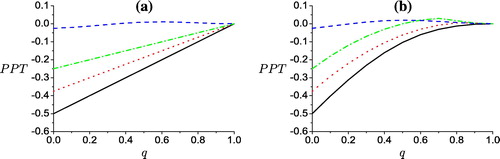
Fig. 1(b) describes the dynamics of PPT for a system subject to local identical non-correlated noise. Two classes of initial states are considered as input states: maximum and partial entangled state. The output state turns into a separable state at q = 1 for a system prepared initially in maximum entangled state. However, starting from partial entangled class as an input state, the PPT is violated for small values of q.

It is important to quantify the amount of entanglement which is still survival on the traveling channels through the local noise environment. For this purpose, we use the negativity as a measure of entanglement. This measure is introduced by Zyczkowski et al. (1998), which depends on the eigenvalues of the partial transpose of the output state.(11) where λ_i,i = 1 … 4 are the eigenvalues of the partial transpose of the states (4)(4) and (7)(7) .

In Fig. 2(a) the entanglement dynamics is displayed for different classes of initial states. It is clear that, for maximum entangled state interacts locally with the noise channel (2)(2) , the entanglement of the output state 1 at q = 0. As soon as the interaction goes on, the entanglement decreases as the noise parameter increases. Starting from partial entangled state, the entanglement of the output state vanishes much earlier. This is clear for the class which is characterized by c₁ = c₂ = 0.9 and c₃ = 0.7, where the entangled vanishes at q = 0.4 and at q = 0.2 in the presence of identical non-correlated noise

Figure 2 The dynamic of entanglement for different initial entangled states as defined in Fig. 1 (a) for correlated noise(b) for non-correlated noise.

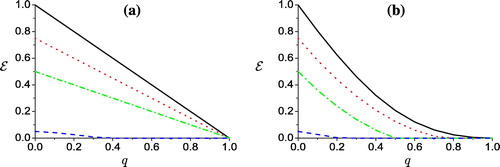
The dynamics of entanglement, is shown in Fig. 2(b). It is clear that, in general decreases as one increases q. For a system initially prepared in MES, the degree of entanglement , is maximum at q = 0, while it completely vanishes at q = 1. However, for PES as initial state, the degree of entanglement decreases faster and vanishes much earlier.

From Fig. 2a and b, one concludes that, the local identical non-correlated noise turns the input entangled states to separable one faster than that depicted for the identical correlated noise. However, the entanglement decays gradually in the presence of identical non-correlated noise, while in the presence of the local identical correlated noise, the entanglement decays hastily.

4 Channel Capacity

The channel capacity is one of the most important topics of the quantum information. In fact all quantum information tasks as quantum computation and sending information, depend on the capacity of the channel. Therefore, it is important to evaluate the transmission rate of information from a sender (Alice) to a receiver (Bob). The capacity of the channel is given by,(12) where , D = 2 is the dimension of ρ_a and is the von Numann entropy.

Fig. 3(a) describes the behavior of the capacity of the channel (4)(4) for different classes of the initial input states. It is shown that, for a class prepared initially in maximum entangled states, the capacity of (4)(4) decreases as the noise parameter q increases. For a class prepared initially in a partial entangled state, the rate of information transmission is smaller compared with that due to use of maximum entangled state as initial channels . Also, the capacity of (4)(4) for a system prepared initially in maximum entangled state decays faster while, starting from a partial entangled state the capacity of the output state (4)(4) , decays smoothly and gradually.

Figure 3 The dynamics of the capacity of the output channels. The solid curve for a system characterized by c₁ = c₂ = c₃ = −1. The dash and dot curves represent the capacity for a system prepared initially in PES characterized by c₁ = −0.5, c₂ = c₃ = 1 and c₁ = 0,c₂ = c₃ = 1 respectively, for (a) correlated noise (b) non- correlated noise.

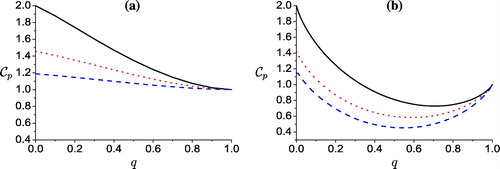
Fig. 3b describes the dynamics of the capacity of the output (9)(9) for different classes of initial states over local identical non-correlated noise. It is clear that, starting from maximum entangled state, the capacity decreases rapidly as q increases, while for partial entangled state the decay of the capacity is smooth and gradual. However, for larger values of q, the capacity (8)(8) increases to reach its maximum value . This shows that the local noise can improve the capacity of the input channel. So we can conclude that initial partial entangled states are more robust than that for the initial maximum entangled states.

5 Teleportation

In this section, we investigate the possibility of using the output channels to perform the original quantum teleportation protocol (Bennett et al., 1993). Assume that the users Alice and Bob share entangled state of Werner type, each qubit interacts locally with its noise environment. This channel is given by Eq. (4)(4) for correlated noise and by Eq. (7)(7) for non-correlated noise. In this context, we assume that Alice is given unknown information coded in the state(13) where ∣β∣² + ∣α∣² = 1. Alice is asked to teleport this state to Bob, who shares with Alice one of the entangled states given by (4)(4) or (7)(7) . The total state of the system is given by for correlated noise and for the non-correlated noise. To implement this protocol, the partners perform the following steps:

1. Alice performs CNOT gate on her qubit and the given state (Corry, 1998). After this operation has been performed the final state of the system is given by(14)

2. Alice applies Hadamard gate (Gershenfeld and Chuang, 1997; Corry, 1998) on her qubit and the given. The output state of the system is defined by(15)

3. Alice performs Bell measurements on the given qubit and her own qubit. Then she transmits her results to Bob via classical channel.

4. As soon as Bob receives the classical data from Alice, he performs suitable unitary operations on his own qubit, depending on the results of Alice’s measurements, to get the original state which Alice teleported.

In this treatment, we assume that the partners Alice and Bob perform the local operations perfectly. However if Alice measures the singlet state , then the final state in Bob’s hand is given by(16) where(17) and α_i, i = 1 … 4 are given by (5)(5) .

To evaluate the quality of the teleported state, we calculate the fidelity, which provides a quantitative measure of the distinguishability of the unknown state (13)(13) , and Bob’s state (16)(16) . The fidelity, of the teleported state is given by,(18) However, if the partners Alice and Bob share the state (7)(7) , where the noise is assumed to be non-correlated, then the initial state of the system is . To achieve the quantum teleportation protocol, Alice and Bob perform the original protocol as described above. If Alice measures ∣ψ₋⟩, then the final state at Bob’s hand is given by,(19) where,(20) and γ_i are given by (8)(8) . In this case, the fidelity of the teleported state (13)(13) by using the channel (7)(7) is given by,(21) The fidelity of the teleported state (13)(13) by using the channels (5)(5) and (7)(7) is plotted in Fig. 4. In general, it is clear that the fidelity of the teleported state depends on the initial channel. For q = 0 the fidelity , if the system is prepared in MES. However, the maximum value of decreases as the entanglement of the initial channel decreases as shown in Fig. 4a. On the other hand, decreases slowly as the noise parameter q increases. The decay of over channels prepared initially in MES is much larger than those transmitted over partial entangled state PES.

Figure 4 The fidelity of the teleported state via a quantum channel subject to local identical noise. The solid curve for a system prepared initially in MES with c₁ = −1,c₂ = c₃ = 1, the dash and dot curves for a system prepared initially in PES with c₁ = 0,c₂ = c₃ = 1, c₁ = 0.5,c₂ = c₃ = 1, and with β = 0.2 for all cases. (a) correlated noise and (b) non-correlated noise.

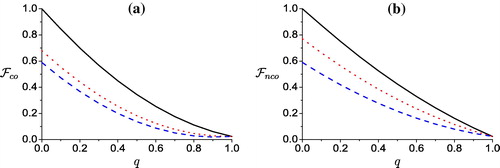
Fig. 4b shows the dynamics of the fidelity of the teleported state in the presence of non-correlated noise. It is clear that the fidelity at q = 0 for the initial channel in MES, and this value decreases as the entanglement decreases. We can see that the fidelity decreases as the channels parameter q increases. The decay of is more rapid over channels prepared initially in MES than in Fig. 4b.

6 Conclusion

In this contribution, we investigate the dynamics of the two-qubit system prepared initially in maximum or partial entangled states. It is assumed that, these states are subject to two different types of noise at the users locations: correlated and non-correlated noise. The entangled channels turn into classical channels as the noise parameter increases. The entangled channel loses its entangled properties faster for correlated noise. However for non-correlated noise, the entangled channels lose their entangled properties gradually and smoothly. This behavior reflects on the dynamics of the survival entanglement, where the entanglement decreases faster in the presence of correlated noise and decreases gradually for non-correlated noise.

The efficiency of the output channel is investigated by means of its capacity. It is clear that, starting from the maximum entangled state, the capacity is maximum (C_p = 2) at q = 0. However as q increases the capacity decreases to reach its minimum value. In the presence of the non-correlated noise, the capacity decreases faster than that depicted for correlated noise. Starting from a class with a lesser degree of entanglement the noise parameter improves the capacity of the quantum channel.

The possibility of using the output channel to perform quantum teleportation is investigated. We show that the fidelity of the teleported state decreases as the noise parameter increases. In the presence of the local correlated noise, the fidelity decreases gradually and smoothly, while it decreases quickly for non-correlated noise.

In conclusion the robustness of the traveling channel over a noise channel depends on the degree of entanglement of initial state and the type of the noise. If the effect of the noise in Alice’s lab is independent from that in Bob’s lab., the entangled channel loses its entanglement properties faster than those if the noise in both labs are dependent. The output channels could be used for quantum teleportation and its efficiency is larger in the presence of correlated noise.

Acknowledgements

We are grateful to the referees for their constructive comments and remarks which have improved the manuscript in many aspects.