Optimal variational iteration method for nonlinear problems

Peer review under responsibility of University of Bahrain.

Abstract

This paper focuses on the study of boundary value problems using well-known He’s variational iteration method which is coupled with an auxiliary parameter. Three examples are given to show the efficiency and importance of the proposed algorithm. The reliability and accuracy has been proved by comparing our results with the solution obtained by standard variational iteration method.

Keywords:

• Auxiliary parameter
• Variational iteration method
• Boundary value problems
• Error estimate

1 Introduction

Inokuti et al. (1978) proposed a general Lagrange multiplier method to solve nonlinear problems especially in the field of quantum mechanics. Later on, He (1999, 2000, 2007) modified the method to a new kind of an analytical technique for nonlinear problems and named it as variational iteration method (VIM), which is effectively and easily used to obtain solution of nonlinear equations accurately. For example, Belgacem et al. (2015) and Baskonus et al. (2015) obtain solutions of nonlinear fractional differential equations systems (NFDES) through implementation of VIM and concluded that VIM remains a valuable tool for the treatments of NFDES. Bulut and Baskonus (2009) obtain an exact solution of dispersive equation. Wazwaz (2007a, 2007b, 2007c, 2008) applied the method to nonlinear differential equations and pointed out that VIM is a very effective and reliable analytical tool for solving these equations. Saberi and Tamamgar (2008) concluded that the method is highly reliable for integro-differential equations. Goh et al. (2009) applied the method to hyperchaotic system with great success. Uremen and Yildirim (2009) and Sadighi and Ganji (2007) obtain exact solutions of poisson equation and nonlinear diffusion equations respectively. With the passage of time, several modifications were made in He’s VIM, which have further improved the efficiency and accuracy of the iterative algorithm to a tangible level.

Figure 1 Absolute residual error for the problem (27) at 5th order approximation by standard VIM.

Figure 2 Absolute residual error for the problem (27) at 5th order approximation by OVIM, when .

Moreover, with the passage of time many analytical techniques are developed to solve nonlinear problems. Liao (1992) came up with a new idea, he developed a nonlinear analytical technique called homotopy analysis method (HAM), which is free from assumption of small parameters and can be used to obtain approximate solution of nonlinear problems. In this method, Liao inserted an auxiliary parameter h, which is used to control the convergence of an approximate solution over the domain of the problem. Liao (2003), further generalized the method so called optimal homotopy analysis method (OHAM) for strongly nonlinear differential equations by inserting multiple parameters, which are used to control the convergence of approximate solutions. The optimal value of auxiliary parameters is obtained by minimizing the absolute residual error, which is a reliable, effective and accurate method even for higher order of approximation. Different available studies that used the OHAM to solve various nonlinear equations can be seen in the literature (Xu et al., 2015; Nawaz et al., 2015; Ellahi et al., 2015a, 2015b; Zeeshan et al., 2014, 2016).

In this paper, an auxiliary parameter is inserted into the correctional functional of VIM for boundary value problems. We consume all of the boundary conditions to establish an integral equation before constructing an iterative algorithm to obtain an approximate solution. Thus we establish a modified iterative algorithm that does not contain undetermined coefficients, whereas most previous iterative methods do incorporate undetermined coefficients. It is observed that the coupling algorithm provides a convenient way to control and adjust the convergence region of approximate solution over the domain of the problem. Three examples are given to explicitly reveal the performance and reliability of the suggested algorithm.

2 Variational iteration method (VIM)

To illustrate the steps of variational iteration method, we consider the following general nonlinear ordinary differential equation.(1) where and are linear and nonlinear operator respectively and illustrates an inhomogeneous term. According to VIM (He, 1999, 2000, 2007; Noor and Mohyud-Din, 2008), we can construct the correction functional as follows(2) where is a Lagrange multiplier (He, 1999, 2000, 2007; Noor and Mohyud-Din, 2008), which can be identified optimally via variational theory, is the nth approximate solution, and is consider as a restricted variation, i.e. . After identification of Lagrange multiplier, the successive approximations , of the solution can be readily obtained. Consequently, the exact solution will be of the form:(3)

3 Optimal variational iteration method (OVIM)

To illustrate the steps of optimal variational iteration method, we consider the following second order nonlinear ordinary differential equation.(4) subject to the boundary conditions(5) where is the linear differential operator, represents the nonlinear operator and illustrate an inhomogeneous term. According to standard VIM, the correction functional is given as(6)

Making the correction functional stationary, the Lagrange multiplier is identified as (Noor and Mohyud-Din, 2008; Xu, 2009), we get the following iterative formula(7)

An unknown auxiliary parameter can be inserted into the iterative formula (7), for , Eq. (7), becomes(8) for optimal variational iteration method, we will proceed as follows,

From Eq. (8),(9)

Substituting and in Eq. (9) and solve for , we get

Substituting the value of and in Eq. (9) yields(10) which can be solved by the modified iterative algorithm as(11)

The Iterative algorithm (11) does not contain undetermined coefficients. contain only an auxiliary parameter , which is used to control the convergence of approximate solution that can be determined optimally by minimizing the norm 2 of the residual function over the domain of given problem (Hosseini et al., 2010a, 2010b, 2012).

4 Numerical examples

In this section, we use Optimal Variational Iteration Method (OVIM) to find an approximate solution of boundary value problems. Numerical results obtained by the developed iterative algorithm are very encouraging.

Example 4.1

Consider the following fourth order boundary value problem (Mohyud-Din et al., 2010).(12) subject to the boundary conditions

The exact solution for this problem is(13)

According to standard VIM, the correction functional is given as(14)

Making the correction functional stationary, the Lagrange multiplier is identified as (Noor and Mohyud-Din, 2008; Xu, 2009), we get the following iterative formula(15)

Consuming the initial conditions, we have the following approximantswhere and can be calculated using the boundary conditions corresponding to different values of parameter .

According to OVIM, we will proceed as follows,(16) using the boundary conditions, we get

Consequently, we have the following iterative algorithm(17) we obtain the following approximationswe define the following residual function, to obtain the proper value of for the series solution (17),(18) and the error of norm 2 of residual function (18) is,(19)

The above residual function can be used to approximate and the optimal value of can be determined by minimizing the residual error given in Eq. (19). Table 1 exhibits the errors obtained using the optimal variational iteration method (OVIM) and variational iteration method (VIM) corresponding to different values of parameter It is obvious that the results of OVIM are more reliable and accurate than VIM.

Example 4.2

Consider the following second order nonlinear differential equation, the temperature distribution equation in a uniformly thick rectangular fin radiation to free space with non-linearity of high order (Marinca and Herisanu, 2008).(20) subject to the boundary conditions

According to standard VIM, the correction functional is given as(21)

Making the correction functional stationary, the Lagrange multiplier is identified as (Noor and Mohyud-Din, 2008; Xu, 2009), we get the following iterative formula(22)

Consuming the initial condition, we have the following approximantswhere can be calculated using the boundary condition corresponding to different values of parameter .

According to OVIM, we will proceed as follows,(23) using the boundary conditions, we get

Consequently, we have the following iterative algorithm(24) we obtain the following approximationswe define the following residual function,(25) and the error of norm 2 of residual function (25) is,(26)

The optimal value of can be determined by minimizing the residual error given in Eq. (26). Table 2 exhibits the errors obtained using the optimal variational iteration method (OVIM) and variational iteration method (VIM) corresponding to different values of parameter It is obvious that the results of OVIM are better and more accurate than VIM.

Example 4.3

Consider non-dimensional steady state reactive transport model, so-called nonlinear reaction diffusion model in porous catalysts which has been used to study porous catalyst pellets, which is governed by (Semary and Hassan, 2015).(27) subject to the boundary conditions

According to standard VIM, we have the following iterative formula, when and (28)

Consuming the initial condition, we have the following approximantswhere can be calculated using the boundary condition

According to OVIM, we will proceed as follows,(29) using the boundary conditions, we get

Consequently, we have the following iterative algorithm(30) we obtain the following approximationswe define the following residual function,(31) and the error of norm 2 of residual function (31) is,(32)

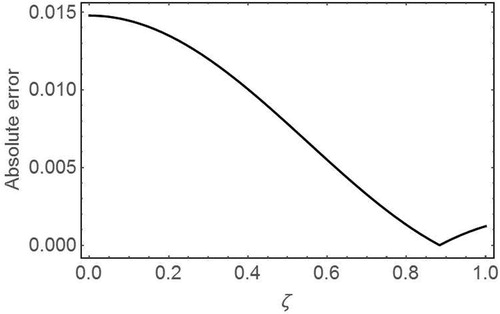
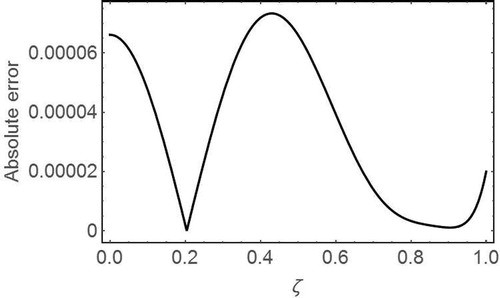
The minimum point of as , is obtained. By substituting in , the absolute error at 5th order approximation by OVIM reduces remarkably (see Figs. 1 and 2).

Table 1 Error estimates: error = Abs (exact solution − approximate solution).

↓				Error (VIM)				Error (VIM)
	Exact	Approximate	Error (OVIM)		Exact	Approximate	Error (OVIM)
0	1	1	0	0	1	1	0	0
0.1	1.105170	1.105170	9.75E−7	7.91E−7	1.105170	1.105170	1.27E−6	2.51E−7
0.2	1.221340	1.221340	6.58E−7	0.000020	1.221340	1.221340	5.61E−7	0.000015
0.3	1.349520	1.349520	5.70E−7	0.000485	1.349520	1.349520	1.44E−7	0.001280
0.4	1.490750	1.490750	6.85E−7	0.011451	1.490750	1.490750	4.64E−8	0.111747
0.5	1.646100	1.646090	8.01E−7	0.270513	1.646100	1.646090	1.04E−7	9.337910
0.6	1.816650	1.816650	8.60E−7	6.382930	1.816650	1.816650	3.01E−7	628.7880
0.7	2.003580	2.003580	7.90E−7	149.2260	2.003580	2.003580	4.63E−7	27217.50
0.8	2.208110	2.208100	1.08E−6	3368.650	2.208110	2.208100	1.14E−6	634860.0
0.9	2.431520	2.431510	1.98E−6	70385.10	2.431520	2.431510	2.70E−6	5,764,110
1	2.675200	2.675200	2.6E−12	1,307,730	2.675200	2.675200	5.7E−12	0.046360

Table 2 Error estimates: error = Abs (numerical solution − approximate solution).

				Error (VIM)				Error (VIM)
	Numerical	Approximate	Error (OVIM)		Numerical	Approximate	Error (OVIM)
0	0.956820	0.956821	4.66E−7	0.677522	0.852329	0.852460	1.31E−4	0.202374
0.1	0.957240	0.957240	4.56E−7	0.680675	0.853650	0.853780	1.30E−4	0.204153
0.2	0.958499	0.958499	4.36E−7	0.690197	0.857629	0.857756	1.28E−4	0.209547
0.3	0.960602	0.960603	4.16E−7	0.706274	0.864315	0.864438	1.23E−4	0.218732
0.4	0.963557	0.963558	3.90E−7	0.729233	0.873795	0.873912	1.16E−4	0.232020
0.5	0.967375	0.967375	3.51E−7	0.759557	0.886194	0.886301	1.07E−4	0.249886
0.6	0.972068	0.972068	3.03E−7	0.797918	0.901681	0.901777	9.58E−5	0.273022
0.7	0.977655	0.977655	2.45E−7	0.845227	0.920478	0.920559	8.12E−5	0.302408
0.8	0.984155	0.984155	1.79E−7	0.902696	0.942871	0.942934	6.21E−5	0.339434
0.9	0.991594	0.991594	9.60E−8	0.971948	0.969224	0.969261	3.64E−5	0.386100
1	1.000000	1.000000	1.03E−8	1.055160	1.000000	1.000000	6.35E−8	0.445335

5 Conclusion

The proposed study is based on a variational iteration method coupled with an auxiliary parameter to obtain an approximate solution of the ordinary differential equations with boundary conditions. An optimal auxiliary parameter can be determined by minimizing the residual function over the domain of the problem. Graphical representation and numerical results demonstrate the complete reliability and efficiency of the developed algorithm.

Notes

Peer review under responsibility of University of Bahrain.