Effects of second-order slip on the flow of a fractional Maxwell MHD fluid

Peer review under responsibility of University of Bahrain.

Abstract

The magnetohydrodynamic (MHD) flow of a generalized Maxwell fluid induced by a moving plate has been investigated, where the second-order slip between the wall and the fluid in the wall is considered. The fractional calculus approach is used to establish the constitutive relationship model of the non-Newtonian fluid model. Exact analytical solutions for the velocity field and shear stress in terms of Fox H-function are obtained by means of the Laplace transform. The solutions for the generalized Maxwell second-order slip model without magnetic field, the MHD flow of generalized Maxwell flow without slip effects or first-order slip model can be derived as the special cases. Furthermore, the influence of the order of fractional derivative, the magnetic body force, the slip coefficients and power index on the velocity and shear stress are analyzed and discussed in detail. The results show that the velocity corresponding to flows with slip condition is lower than that for flow with non-slip conditions, and the velocity with second-slip condition is lower than that with first-order slip condition.

Keywords:

• Second-order slip
• Generalized Maxwell fluid
• MHD flow
• Fox H-function

1 Introduction

There are many physical phenomenons actually with incomplete viscoelastic fluid in engineering and industry, such as polymer solutions, exotic lubricants, colloidal and suspension solutions, food stuffs, synthetic propellants, molten plastics and many others. These fluids have been modeled in a number of diverse manners with their constitutive equations varying greatly in complexity, among which the viscoelastic Maxwell fluid model has been studied widely (Fetecau and Fetecau, 2004; Tan and Masuoka, 2007; Jamil et al., 2011; Abbasbandy et al., 2014"). The Maxwell model can be represented by a purely viscous damper and a purely elastic spring connected in series (Christensen, 1971), which has been proposed to describe the behavior of viscoelastic fluids, and has had some success in describing polymeric liquids, it being more amenable to analysis and more importantly experimental.

Fig. 1 Without slip effect, velocity field and shear stress for various values of the fractional parameter .

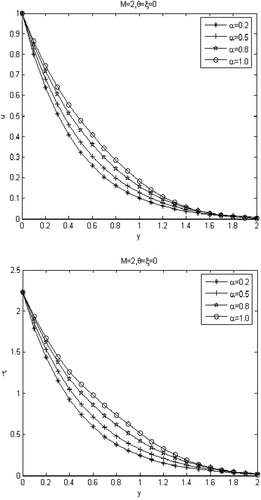
Fig. 2 With first-order slip effect, velocity field and shear stress for various values of the fractional parameter .

Fig. 3 With second-order slip effect, velocity field and shear stress for various values of the fractional parameter .

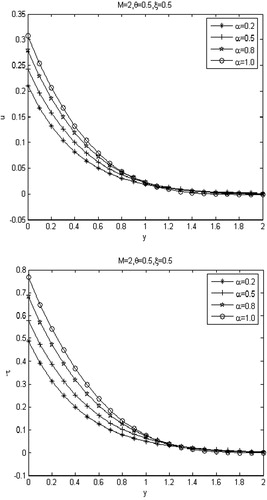
Fig. 4 Without slip effect, velocity field and shear stress for various values of the magnetic parameter M.

Fig. 5 With first-order slip effect, velocity field and shear stress for various values of the magnetic parameter M.

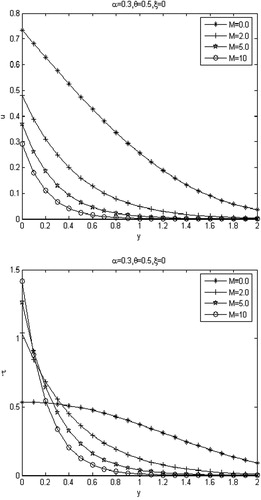
Fig. 6 With second-order slip effect, velocity field and shear stress for various values of the magnetic parameter M.

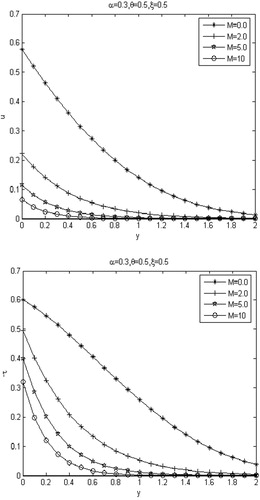
Fig. 7 Profiles of the dimensionless velocity field and shear stress with various values of the first-order slip parameter .

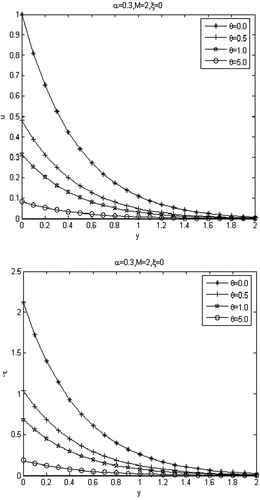
Fig. 8 Profiles of the dimensionless velocity field and shear stress with various values of the second-order slip parameter .

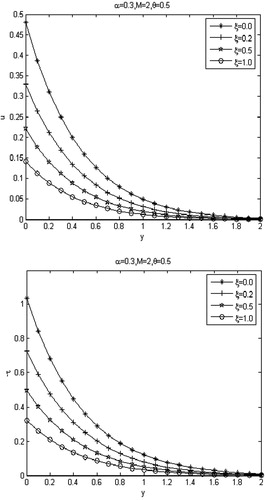
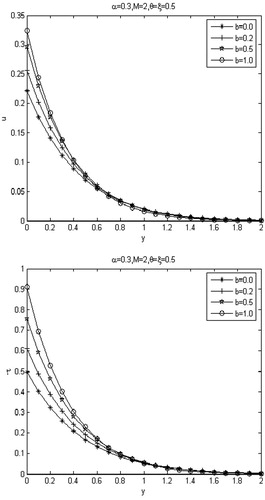
Fig. 9 Without slip effect, profiles of the dimensionless velocity field and shear stress with various values of power index b.

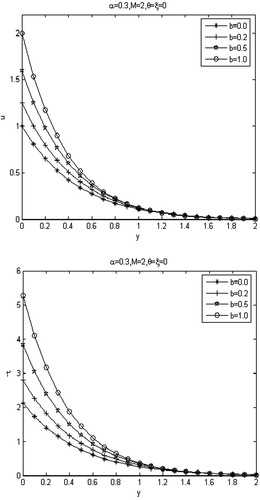
Fig. 10 With first-order slip effect, profiles of the dimensionless velocity field and shear stress with various values of power index b.

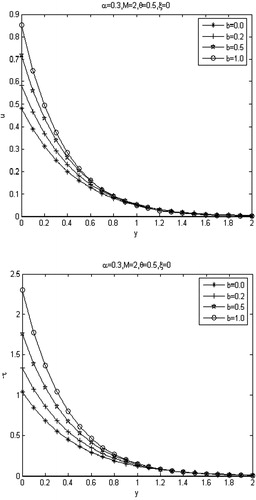
Fig. 11 With second-order slip effect, profiles of the dimensionless velocity field and shear stress with various values of power index b.

Rheological constitutive equations with fractional derivatives (Podlubny, 1999; Song and Jiang, 1998; Imran et al., 2017") have been proved to be a valuable tool to describe the behaviors of viscoelastic properties. The fractional derivative models of the viscoelastic fluids are derived from classical equations, which are modified by replacing the time derivative of an integer order by precisely non-integer order integrals or derivatives.With the development of research, the fractional derivative models of the viscoelastic fluids are concerned by considerable researchers. Song and Jiang, 1998 used the fractional calculus to analyze the experiment data of viscoelastic gum and obtained satisfactory results. Fetecau et al., 2008 investigated the unsteady flow of a second-grade fluid induced by the time-dependent motion of a plate between two side walls perpendicular to the plate. Xue et al., 2008 and Xue and Nie, 2009 discussed the exact solutions of the Rayleigh-Stokes problem for a heated generalized viscoelastic fluid in a porous half-space. Jamil et al., 2011 researched the unsteady flow of an incompressible Maxwell fluid with fractional derivative induced by a sudden moved plate, and analyzed the influence of the material and the fractional parameters on the fluid motion. Qi and Guo, 2014 studied a new heat conduction equation which is based on the time-nonlocal generalized of Fourier law, the exact solution of an initial-boundary value problem was studied and presented under series forms. Fan et al., 2015 presented an inverse problem to estimate parameters in generalized fractional Zener model based on the Bayesian method, and performed some examples to certify the validity of the method. Imran et al., 2017 investigated some natural convection flows of differential type fluids with Caputo fractional derivatives, and solved the velocity fields using Laplace transform method.

The assumption that a liquid adheres to a solid boundary so called no-slip boundary condition has been proved to be inadequate in several situations such as: the mechanics of thin fluids, flows in micro-channels, or flows of polymeric liquids with high molecular weight. For describing the slip that occurs at solid boundaries, a large number of models have been proposed. In recent years, Ebaid, 2008 studied the effects of magnetic field and wall slip conditions on the peristaltic transport of a Newtonian fluid in an asymmetric channel. Jamil and Khan, 2011 considered the first order slip effect on fractional Maxwell fluids, and obtained the solutions of velocity field and shear stress. Vieru and Rauf, 2011 and Vieru and Zafar, 2013" investigated some Couette flows and Stokes flows of a Maxwell fluid with slip condition. The exact solutions of generalized Oldroyd-B fluid flow with the slip effects were obtained by Zheng et al., 2012. Han et al., 2015 presented a slip flow of a generalized Burgers’ fluid between two side walls generalized by an exponential accelerating plate and a constant pressure, the analytical solutions are established and analyzed. Akbar and Khan, 2016a given the numerical study of carbon nanotubes suspended magnetohydrodynamic(MHD) stagnation point flow over a stretching sheet with convective slip. Shakeel et al., 2016 studied the flows of an Oldroyd-B fluid under the consideration of slip condition at the boundary, the fluid motion is generated by the flat plate which has a translational motion in its plane with a time-dependent velocity. Hayat et al., 2016 investigated the unsteady MHD flow over exponentially stretching sheet with velocity and thermal slip boundary conditions, and analyzed various pertinent parameters on the axial velocity and temperature distributions.

The motivation of the present study is to find the velocity field and shear stress corresponding to the second-order slip flow of a generalized Maxwell fluid over a plate with the assumption of low-magnetic Reynolds number. The fractional calculus approach is used to establish the constitutive relationship of the non-Newtonian fluid model. The exact solutions, obtained by means of a finite Fourier sine transform and a discrete Laplace transform, are presented using series forms in terms of the Fox H-function. The solutions of generalized Maxwell fluid without magnetic field effect, or the first-order slip, or without slip can be recovered from our solutions. Finally, the influence of the material, slip, fractional, magnetic and index parameters on the motion of generalized Maxwell fluids are underlined by graphical illustrations. The difference among generalized Maxwell fluid and classical Maxwell fluid models is also analyzed.

2 Governing equations

The constitutive equations for an incompressible fluid are given by(1) where is the Cauchy stress tensor, is the velocity vector, is the constant density of the fluid, is the body force field. There we consider the MHD fluid, which is affected by magnetic field . We neglected the induced magnetic field by assuming very large magnetic diffusivity. It is also assumed that no electric field is applied.

The constitutive equation of an incompressible Maxwell fluid is written in the form (Fetecau and Fetecau, 2004; Tan and Masuoka, 2007; Han et al., 2015"):(2) where(3) and denotes the indeterminate spherical stress, is the extra-stress tensor, is the first Rivlin–Ericksen tensor, is the velocity gradient, are material constants, known as the viscosity coefficient, the relaxation times, respectively. If , the Eq. (2) is the constitutive equation of a Newtonian fluid.

We consider the fluid is permeated by an imposed uniform magnetic field which acts in the positive -coordinate (Jamil et al., 2013; Akbar and Khan, 2016b; Akbar et al., 2016a,Akbar et al., 2016b,Akbar et al., 2016c"), by assuming a very small magnetic Reynolds number, the induced magnetic field is neglected. Hence, the Lorentz force caused by the external magnetic field can be represented as (, 0, 0). is the magnitude of and is the electrical conductivity of the fluid, u denotes the x-component of the fluid velocity. The velocity and shear stress for one dimensional flow take the form:(4) where is the unit vectors in the x-direction. For this flow, the constant of incompressible is automatically satisfied. Taking account of the initial condition and in the absence of pressure gradient in the -direction, the motion equation of the generalized Maxwell fluid is:(5) (6) where is the shear stress that is different of zero, is the kinematic viscosity, and .

The governing equations corresponding to a unsteady generalized Maxwell fluid with fractional derivative, performing the same motion are(7) (8) where is the fractional parameter and the fractional operator based on Riemann– Liouville’s definition (Podlubny, 1999) is(9) where is the Gamma function. If , Eqs. (7) and (8) are the governing equations of classical Maxwell fluid.

3 Statement of the problem and its solutions

Consider the flow of a Maxwell fluid bounded by a extended plate at when the positive y-axis of a Cartesian coordinate system is taken in the upward direction. The Maxwell fluid occupies the space . The fluid is assumed to be electrically conducting and a uniform magnetic fluid is applied normal to the flow direction. Initially, the flow and plate are at rest, and the flow begins to flow due to motion of the plate with velocity A in its own plane at the moment . Here we assume the existence of slip boundary between the velocity of the fluid at the wall and the speed of the wall, and assume that the relative velocity to be related to the velocity gradient and its divergence at the wall. The governing equations can be described by Eqs. (7) and (8) and the corresponding initial and boundary conditions are written as follows:(10) (11) where is a constant, and are two independent coefficients named the slip coefficients. If then the general assumed no-slip boundary condition is obtained. If and are finite, second-order slip occurs. The first order slip is obtained by dropping the second order derivative term. Furthermore, the natural conditions are also satisfied for the fluid is at infinity, and there is no shear stress in the free stream.(12)

In the following, the system of fractional partial differential equations Eqs. (7) and (8), and the associated initial and boundary conditions will be solved. Firstly, employing the non-dimensional quantities in Eqs. (8), (10)–(12)(13)

Dimensionless equations can be given (for brevity the dimensionless mark ‘*’ is omitted here)(14)

The initial and boundary conditions take the form:(15) (16) (17)

Then applying the Laplace transforms principle of sequential fractional derivatives (Sneddon, 1951), and taking into account the initial conditions Eq. (10), yields(18)

Subject to the boundary conditions(19) (20) where () is the image function of (, ) and is the transform parameter. In there, we used the initial value theorem of Laplace transform(21) (22)

Solving Eqs. (18)–(20), we get(23)

The shear stress can be calculated from Eq. (7), taking the Laplace transform of Eq. (7) and introducing Eq. (23), we obtain(24) where is the Laplace transform of . In order to obtain the velocity field and shear stress in reginal space, and to avoid the burdensome calculations of residues and contour integrals, we apply discrete inverse Laplace transform to get to the velocity and the shear stress. However, for a suitable presentation, we rewrite Eqs. (23) and (24) in series form(25) (26)

In order to ensure the convergence of the solutions, in the process of calculation we have used the Taylor series expansion like , and .

Applying the discrete inverse Laplace transform, we arrive at(27) (28)

In terms of Fox H-function, we rewrite the above equation as the simpler form:(29) (30)

Where the property of the Fox H-function (Mathai et al., 2009; Qi and Guo, 2014") is(31)

Furthermore, to justify the boundary condition Eqs. (16), we have(32) (33) and(34)

We can see that the exact solution Eq. (29) satisfies the boundary condition Eq. (16).

4 Special cases

(1) In the special case when , Eqs. (29) and (30) reduce to(35) (36) which correspond to the flow of a generalized Maxwell fluid without magnetic field effect.

(2) When or dropping the second order derivative term, the first-order slip velocity and shear stress of a generalized Maxwell fluid are as follows:(37) (38)

(3) In the special case when , Eqs. (29) and (30) are simplified into(39) (40)

Which are the solutions for the MHD flow of a generalized Maxwell fluid without slip effect.

(4) When in Eqs. (39) and (40), we obtain similar solutions for a generalized Maxwell fluid performing the same motion as obtained in Reference Fetecau et al., 2009.

5 Results and discussion

The purpose of this paper is to analyze the unsteady flow of an incompressible generalized Maxwell MHD fluid under the second-order slip boundary condition between the fluid and the wall, the relative velocity between the fluid at the wall and the wall is assumed to be related to the velocity gradient and its divergence at the wall. The exact solutions for the velocity field and shear stress in terms of Fox H-function are obtained using the Laplace transform. For a complete study and for possible comparisons, we present the limiting cases of velocity field and shear stress by making , or , our solutions reduce to those corresponding to the generalized Maxwell second-order slip model without magnetic field, the MHD flow of generalized Maxwell flow first-order slip effect or without slip model, respectively. In order to reveal some relevant physical aspects of the obtained results, some figures are plotted by using the analytical solutions obtained in Section 3, which we presented in Figs. 1–11.

Figs. 1–3 are depicted to show the changes of the velocity field and shear stress with the fractional parameters for without slip model, first-order slip model and second-order slip model respectively. It is clearly seen that the smaller the values of , the more rapidly the velocity and shear stress decays. indicates that the fluid is classical Maxwell fluid, which has the smaller velocity decay than that of fractional Maxwell fluid. 4–6 show the influence of the magnetic field on the velocity field and shear stress(in absolute value) without slip effect, first-order slip and second-order slip effects. We can see that the magnetic body force is favorable to the velocity decays, and the more the values of , the more rapidly the velocity decays. This is due to the fact that applied transverse magnetic field produces a drag in the form of Lorentz force thereby decreasing the magnitude of velocity. Figs. 7,8 demonstrate the influence of slip parameters and on the motion of the fluid respectively. It is noted that the velocity and shear stress (in absolute value) are smaller when slip parameters are nonzero. With the increase in slip parameters and , the velocity and shear stress decrease as expected. The velocity of second-order slip model decays more rapidly than first-order slip model. 9–11 show the velocity and shear stress changes for various values of power index b. It can be seen that the strongest shear stress takes place in the boundary between the Maxwell fluid and the moving plate, with the increasing values of b, the flow velocity and shear stress increase rapidly, and away from the plate the flow velocity and shear stress decrease rapidly.

6 Conclusions

In this paper, the unsteady MHD Maxwell fluid under the effect of second-order slip boundary condition are considered. The governing equations of the generalized Maxwell fluid flow are established using fractional derivative, and the analytical solutions of velocity field and shear stress are obtained by applying integral transform. Furthermore, some figures are plotted to discuss the effect of various parameters. We analyzed some special cases of our results, one of which is consistent with the results in Reference Fetecau et al., 2009. Thus, our results provide a new model and analytical theory for studying the slip flow of viscoelastic fluid and other engineering problems.

Conflict of interest

The authors have no conflict of interest.

Acknowledgements

The work is supported by the China Postdoctoral Science Foundation (No. 2015M 580069) and Beijing Information Science and Technology University Research Foundation (No. 1725009).

Notes

Peer review under responsibility of University of Bahrain.