Stochastic solution for Cauchy one-dimensional advection model in mean square calculus

Peer review under responsibility of University of Bahrain.

Abstract

This work is concerned with the discussion of the numerical approximation for random Cauchy transport model in one dimension. The random (forward time, backward space) finite difference scheme is used to find the stochastic solution. The impression of the consistency and the random von-Neumann stability technique under the mean square sense are studied. Using some examples, we can support our main objective of this model statistically.

Keywords:

• Mean square convergence
• Finite difference scheme
• Random Cauchy problem
• Random von-Neumann stability

1 Introduction

Any Partial differential equation (PDE) and also, stochastic approximated partial differential equation (SPDE) are based on the initial and also, on the boundary conditions in order to get a well-posed problem. PDEs and SPDEs appear considerably in all areas of engineering and physics. Furthermore, in recent research area we have seen a dramatic increase in using PDEs and SPDEs for chemistry, biology, computer sciences and economics areas (Tveito and Winther, 2004; Pinchover and Rubinstein, 2005"). Particulary, we will focus on pure random Cauchy one-dimensional advection model. Additionally, we can also restrict ourselves to one spatial dimension. This model is an initial value problem defined on the whole real line. Therefore, we can derive very simple solutions without having to deal with complications related to boundary values (Tveito and Winther, 2004; Pinchover and Rubinstein, 2005; Salsa, 2015").

Fig. 3 Stable case, N = 100, , , , i.e., .

Fig. 4 Unstable case, N = 300, , , , i.e., .

Table

Table

Table

Table

Table

Table

Table

Table

Table

Matlab Codes
1. Example 1
clear
clc
xmin = 0;
xmax = 10;
N = 100;
dt = 0.005;
t = 0.3;
tmax = 2.0;
C = 1.0;
dx = (xmax − xmin)/N;
x = xmin − dx: dx: xmax + dx;
u0 = sin(x);
u = u0;
unp1 = u0;
nsteps = tmax/dt;
for n = 1: nsteps
for i = 2: N + 2
unp1(i) = u(i) − C∗dt/dx∗(u(i) − u(i − 1));
end
t = t  + dt;
u = unp1;
exact = − sin((C∗t) − x);
plot(x,exact,‘b’,‘LineWidth’,4);
hold on
plot(x,u,‘∗’,‘markerfacecolor’,‘r’);
hold off
axis([xmin xmax −0.5 1.5])
xlabel(‘x’, ‘fontsize’, 16)
ylabel(‘U(t,x)’, ‘fontsize’,16)
shg
pause(dt);
end
2. Example 2
clear
clc
xmin = 0;
xmax = 1;
N = 100;
dt = 0.005;
t = 0.09;
tmax = 0.2;
C = 0.5;
dx = (xmax − xmin)/N;
x = xmin − dx: dx: xmax + dx;
u0 = exp(−200∗(x − 0.25).^2);
u = u0;
unp1 = u0;
nsteps = tmax/dt;
for n = 1: nsteps
for i = 2: N + 2
unp1(i) = u(i) − C∗dt/dx∗(u(i) − u(i − 1));
end
t = t + dt;
u = unp1;
exact = exp(−200∗(−x + 0.25 + C∗t).^2);
plot(x,exact,‘b’,‘LineWidth’,4);
hold on
plot(x,u,‘∗’,‘markerfacecolor’,‘r’);
hold off
axis([xmin xmax −0.5 1.5])
xlabel(‘x’, ‘fontsize’, 16)
ylabel(‘U(t,x)’, ‘fontsize’,16)
shg
pause(dt);
end

The convection is a kind of heat transfer, it takes place in liquids and gases only because liquids and gases have a physical movement. Additionally, the convection transfers a large mass of particles from a hot part of a fluid that rises to a cooler part that sinks (Carslaw, 1921; Lienhard, 2013"). The random models or random methods are much more important than in deterministic case, so our work aims on developing a finite difference scheme from deterministic case to random case when dealing with SPDEs instead of PDEs. Additionally, we aim to prove the consistency and stability of the finite difference scheme in random case by applying the mean square calculus. Therefore, in this paper we will study the stochastic advection model using the finite difference technique and try to find the effectiveness of our random input in the model. In fact, the theoretical discussion of PDEs or SPDEs is not merely of vital interest, but rather has many applications as physical models, biological models, etc., in our life. It is not mechanically obvious that any model is really consistent in the sense that it derives a solvable PDE. Moreover, it is required in most cases that the solution will be unique and stable under small disturbances of the data (Logan, 2014; Wang, 1994; Trim, 1990"). A partial differential problem (PDE) is a relation between an unknown function and its partial derivatives also; it is supplemented by additional conditions like initial conditions or boundary conditions. If we have the PDE with initial condition only, then it is called mathematically a pure IVP or Cauchy problem (Logan, 2014). In this work, we will discuss numerically the random Cauchy problem advection model in dimension with unbounded spatial domain as in the form:(1) where c is assumed to be a random variable, such thatwhere are the space and the time coordinates, respectively. c is a random variable defined on a probability space (, , ) (where is the space of elementary events, is the -algebra of subsets of (i.e., collection of events) and is the probability measure) and is an initial deterministic data function. In the deterministic case, we can interpret the model (1) as the transport of interested quantities with the fluid flow. As in the example, consider a horizontal pipe filled with water that flows from the left to the right with constant velocity. The advection model in physics and engineering is the substance transport and the properties of this substance are carried along with a flow by conserved properties like energy. It governs the motion of a conserved scalar field. The fluid can be any material that contains thermal energy as water or air. Mathematically, this model as fluid’s motion is presented as a vector field and the transported material is described as a scalar field showing its distribution along of the flow direction (Trim, 1990). In some models for our problem (1), the velocity field may be a function of the unknown variable or depends on the space variable (Piterbarg and Ostrovskii, 2013), but here the velocity field will be a random variable when the field flow is random. We can call our problem (1), the advection model with random flow.

There are analytical and numerical processing such as finite difference method, finite volume method, finite element technique, method of lines and others for dealing with the advection model; where the velocity field coefficient is constant or deterministic function also, this model has been discussed in one, two and three dimensions (Ames, 2014; Hugo and Thuburn, 2011"). Additionally, in Jardak et al. (2002), the spectral solution of the Stochastic Advection Equation has been discussed and (Piterbarg and Ostrovskii, 2013; Holt, 2012; Landahl and Mollo-Christensen, 1992") also studied Advection and diffusion in random media. Some papers have been discussed that concerned with the von-Neumann technique (The basic idea of von Neumann’s method is to compare the growth of the analytical and discrete particular solutions) in order to find the stability control for the finite difference schemes according to the advection model (Smith, 1985) and others studied the consistency and stability under mean square calculus for the finite difference method in order to solve the initial value boundary conditions for some partial differential equations (Sohaly, 2014; El-Tawil and Sohaly, 2011; Yassen et al., 2016; Cortes et al., 2007"). The main goal in this work is to find what is the condition on the random velocity coefficient to prove the consistency and the von-Neumann stability for our random difference scheme we use to solve model (1) under mean square sense.

This paper has been partitioned into six parts, each of which deals with one specific topic. In general, we interleave the next parts with the preliminaries part that presents some points used in our discussion. Section 3, studies the finite difference technique for the model (1). Moreover, we will discuss the proof of consistency using the von-Neumann stability in mean square sense for our scheme. Section 4, numerical approximations for some models are computed with its statistical mean. Section 5, is devoted to the conclusion and references.

2 Preliminaries

In this part of the paper, we introduce some definitions and some important remarks to service our technique that is used in our paper. A real random variable on a probability space (, , ) and satisfying the property thatis called 2nd order random variable where, denotes the expectation value operator. If , then the norm is defined as

Definition 1

Thomas, 2013; Soong, 1973"

The finite difference scheme (FDS) (where is the discretization operator, is the approximation solution and denotes whatever the approximation has been made of the source term) is pointwise consistent with the partial differential problem (where is the differential operator, is the solution of the RPDE and is the source term) at () if for any smooth function , and are integersas and .

Definition 2

Smith, 1985

Von-Neumann stability analysis

In the space of our function, we have the Fourier expansionwhere is the Fourier frequencies. We just take one Fourier term

Evaluating this term at the , we get

Also, we can get for instance,(2)

Directly, these previous terms can be plugged into the finite difference scheme and subsequently, define the Growth factor in the form

for stability and for all frequencies. Geometrically, is given by the length of the line segment from the origin to the ellipse centered at . The scheme is stable if the ellipse lies entirely on and within the unit circle. In some cases, the stability may be conditional which limits in a function of .

Proposition 1

Soong, 1973

A sequence is convergent under mean square to a random variable if

3 Random difference scheme

The principle of finite difference technique is close to the approximation schemes used to solve deterministic (stochastic) ordinary and partial differential equations (Smith, 1985; Sohaly, 2014, El-Tawil and Sohaly, 2011; Yassen et al., 2016, Recktenwald, 2004; Mitchell and Griffths, 1980"). The basic idea of this technique is to replace the spatial derivatives in the model (1) by a spatial difference operator at a location by using the neighboring nodal points. Let we define the grid cells for the space to be = () for and also, define the time steps to be = () for . Consider = approximates the exact solution for the problem (1) as, at the point . By replacing the first derivatives in (1) with the difference formulas, we can have the difference scheme as follows:

Using the first-order forward difference for approximating

Then,

Using the first-order backward difference for approximating

Then,

By using these approximations we can motivate the following scheme

Hence, the random finite difference scheme for the problem (1) is(3) where . The consistency, the stability and the convergence are important (useful) topics in deterministic and stochastic theories for several approximation methods as shown in Thomas (2013). As well, the aim of this paper is to appropriate these topics to the problem (1) in mean square space. This viewpoint implies that we concentrate on applying the consistency under mean square calculus and mean square stability for the problem (1) as shown in the next sub-sections.

3.1 Consistency of RFDS (2)

From the definition (1) we can have the following definition.

Definition 3

A random finite difference scheme (RFDS) (where is the discretization operator, is the approximation solution and pointed to the approximation has been made of the source term) that approximating the random partial differential equation (RPDE) (where is the differential operator, is the solution of the RPDE and is the source term) is consistent in mean square ifas

Theorem 1

The RDS (2)(2) that according to the problem (1)(1) is mean square consistent such that , .

Proof

Assume is a smooth deterministic data function

According to (1(1) )where denotes the differential operator for our problem at the mesh point .

According to (2(2) )where denotes the discretization operator for our difference scheme at the point . Then,where

is the domain of the random variable and is the probability distribution of the random variable .

Hence,

Finally,

3.2 Von-Neumann stability in random case for RFDS (2)

The von-Neumann method offers a simple way of assessing the stability properties of linear schemes with constant coefficients. This method is based on the Fourier decomposition of the numerical scheme from which a stability estimate follows (Charles, 2007). In this paper we will use this method when the velocity coefficient in our model (1) is a random variable.

Theorem 2

The RFDS (2)(2) is stable in mean square sense under the conditions:

(1)	The random velocity coefficient must be bounded i.e., .

(2)

, .

Proof

Assume that the Fourier expansion in space of our function iswhere is the Fourier frequencies. As the scheme (2) is for one time step, taking one of the Fourier term , hence at the point , . To simplify notation we can write , then we have:

We define the growth factor as .

For stability, we require for all frequencies. Conditional stability means we only have stability on a certain condition. This condition limits depending on the values of and .

Our scheme is in the formwhere . Inserting in our scheme (2)

Dividing by

Then,we have

Then,

Geometrically, is given by the length of the line segment from the origin to the ellipse centered at . The scheme is stable if the ellipse lies entirely on and with in the unit circle.

Setting

The previous inequality is true for .

For , dividing by yields

Hencei.e.,

The stability condition(4)

Now, we have

Then, for G_​1 ⩽ 1i.e.,

Therefore,

Also, the Growth factorimplies

Recursively, we getwhere is a deterministic function. Hence, The RFDS (2) is conditionally stable under the condition (4). □

4 Case studies

Example 1

Let the scalar motion is advected by a random velocity field along the unbounded spatial domain and for some initial condition as follows(5) where is a bounded random variable. The initial condition(6)

The stochastic analytical solution(7)

The stochastic numerical solution

The random finite difference scheme for this problem is:where and .

From the RFDS (2)

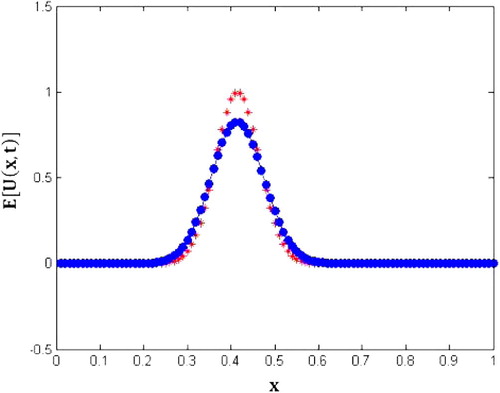
4.1 Verification of the convergence of mean

We can depict the stability condition of this example by the following tables and also, Figs. 1 and 2.

•

•

•

•

Example 2

Let the motion of a scalar is advected by a random velocity field along the unbounded spatial domain and for some initial condition as follows(8) where is a bounded random variable. The initial condition(9)

The stochastic exact solution(10)

The stochastic approximation solution

The random difference scheme for this problem iswhere and .

From the RFDS (2)

Fig. 1 Stable case, N = 100, , , , i.e., .

Fig. 2 Unstable case, N = 1200, , , , i.e., .

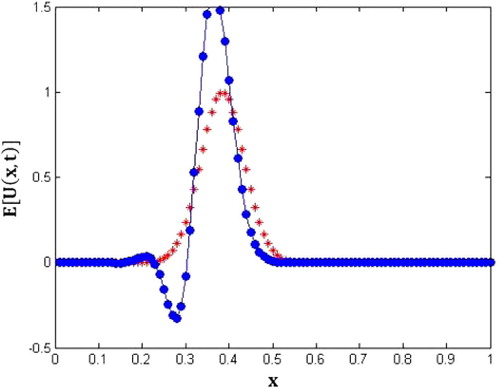
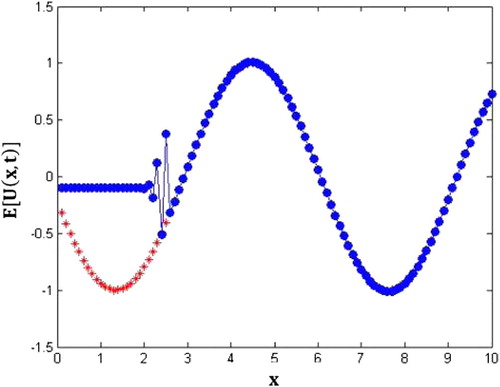
4.2 Verification of the convergence of mean

We can depict the stability condition of this example by the following tables and also, Figs. 3 and 4.

•

•

•

•

5 Conclusion

We have introduced randomness into the velocity coefficient of the transport model and we have proposed a random finite difference scheme (RFDS) for solving this model. Mean square consistency of the RFDS has been studied. The sufficient conditions for the mean square stability of the RFDS has been presented using the von-Neumann technique. The effect of the random velocity coefficient in the advection model must be positively bounded random variable. The numerical experiments displayed that the RFDS we used in this paper gave reliable approximations for the mean of the solution (Figs. 1–4).

Conflict of interest

The authors have no conflict of interest.

Notes

Peer review under responsibility of University of Bahrain.