Truncated series solution of the equation of motion of ions trapped in a radiofrequency quadrupole trap with superimposed octopolar potential

Peer review under responsibility of Taibah University.

Abstract

The power series method is used to solve numerically the equation of motion of ions in a radiofrequency quadrupole ion trap when a small octopolar potential is present. Every time step, the coordinates of the ion are represented by a truncated series of degree 15. The stability diagram of the trap is obtained by using the method to simulate the behavior of hundreds of ions up to a relatively large time. The nonlinear resonance lines are observed. The ion's oscillation frequencies are then studied. Their theoretical expression is derived and compared to the results of the truncated series solution.

Keywords:

• Radiofrequency quadrupole ion trap
• Series solution of the equation of motion
• Stability diagram
• Octopolar potential
• Nonlinear resonances
• Ion's oscillation frequencies

1 Introduction

The radiofrequency quadrupole ion trap is a small and versatile device which allows to maintain ions in a small volume of space by the application of a DC and a radiofrequency voltage. Since its invention in the 1950s by W. Paul and H. Steinwedel, it found multiple applications in physics, chemistry, biology, pharmacology and environmental sciences [1]. It is made of a ring having the radius r₀ closed by two end-caps located at the distance z₀ from the trap's center [2]. Usually $r_0^2=2z_0^2$. The three electrodes have hyperboloidal shape. The end-caps are connected together and a voltage U_DC + V_AC cos Ωt is applied between them and the ring.

Ideally, the potential generated in the volume of the trap is quadrupolar but for real traps it is more complicated. Its general expression in the spherical coordinates (ρ, θ, φ) is given by [3]

(1) $\mathrm{\Phi }(\rho ,\theta )=(U_{\mathrm{DC}}+V_{\mathrm{AC}}cos\mathrm{\Omega }t)\sum _{n=0}^{\infty }{b}_n{\rho }^n{P}_n(cos\theta )$(1) b_n are constants and P_n the Legendre polynomial of order n. If in addition, the trap has a symmetry about the z = 0 plane (z is the trap's axis), only the even terms have to be considered [4]. By taking only the terms of order 2 and 4, the potential (1)(1) $\mathrm{\Phi }(\rho ,\theta )=(U_{\mathrm{DC}}+V_{\mathrm{AC}}cos\mathrm{\Omega }t)\sum _{n=0}^{\infty }{b}_n{\rho }^n{P}_n(cos\theta )$(1) can be written in Cartesian coordinates as [5]

(2) $\mathrm{\Phi }(r,z)=\frac{A_2}{r_0^2}(U_{\mathrm{DC}}+V_{\mathrm{AC}}cos\mathrm{\Omega }t)\left[\frac{r^2}{2}-z^2-\frac{f}{r_0^2}\left(z^4-3r^2{z}^2+\frac{3}{8}{r}^4\right)\right]$(2) A₂ is equal to 1 for ideal traps and f is a constant related to the strength of the octopolar contribution.

The equation of motion for an ion of mass m and charge q under the action of the potential (2)(2) $\mathrm{\Phi }(r,z)=\frac{A_2}{r_0^2}(U_{\mathrm{DC}}+V_{\mathrm{AC}}cos\mathrm{\Omega }t)\left[\frac{r^2}{2}-z^2-\frac{f}{r_0^2}\left(z^4-3r^2{z}^2+\frac{3}{8}{r}^4\right)\right]$(2) is

(3) $\frac{d^{2}u}{d{\tau }^2}+(a_u-2q_u\cos (2\tau )){\mathrm{ug}}_u(r,z)=0$(3) where u = x, y or z, r² = x² + y², $\tau =\frac{\mathrm{\Omega }t}{2}$ and

(4) $\begin{array}{ccc}{g}_{x,y}(r,z)\hfill & =\hfill & 1-\frac{f}{r_0^2}\left(\frac{3}{2}{r}^2-6z^2\right)\hfill \\ g_z(r,z)\hfill & =\hfill & 1-\frac{f}{r_0^2}(3r^2-2z^2)\hfill \end{array}$(4) a_u and q_u are the Mathieu parameters which have the expressions

(5) $\begin{array}{ccc}{a}_z\hfill & =-\frac{8A_2{\mathrm{qU}}_{\mathrm{DC}}}{{\mathrm{mr}}_0^2{\mathrm{\Omega }}^2}=-2a_x=-2a_y\hfill & \hfill \\ q_z\hfill & =\frac{4A_2{\mathrm{qV}}_{\mathrm{AC}}}{{\mathrm{mr}}_0^2{\mathrm{\Omega }}^2}=-2q_x=-2q_y\hfill & \hfill \end{array}$(5)

A trapped ion performs oscillations with the fundamental frequencies ${\omega }_u={\beta }_u\frac{\mathrm{\Omega }}{2}$ [5]. β_u is function of the Mathieu parameters.

The trapping is possible only for q_z and a_z chosen in some regions of the (q_z, a_z) plane. The usual region is called the lowest stability domain and corresponds to β_z and β_x = β_y (noted β_r) having the values between 0 and 1 [6].

Simulations of the trapped ions dynamics in radiofrequency quadrupole ion traps have been realized since decades now [7,8]. The positions and velocities of every ion are calculated by solving numerically the equation of motion or using its analytical solution. The power series method has also been used to solve numerically the ion's equation of motion [9,10]. It allows to get accurate results with a relatively small calculation time. The trajectories of hundreds of ions up to several milliseconds can be calculated very quickly. This is useful when some parameters such as the Mathieu parameters are scanned with small steps. Several thousands of cases can be studied in few hours.

2 Resolution of the trapped ion equation of motion using the power series method

The use of the power series method for the resolution of the trapped ion equation of motion is explained in details in Refs. [9,10]. The variable ξ = Ωt (RF phase) is considered. To calculate the velocity and the position of an ion from t = 0 to t_max, the time step Δt is taken equal to 19% of the RF period $T=\frac{2\pi }{\mathrm{\Omega }}$. For the Nth step the coordinates x, y and z are represented by the truncated series

(6) $\begin{array}{ccc}x\hfill & =\hfill & \sum _{n=0}^{15}{A}_n{(\xi -N\mathrm{\Delta }\xi )}^n\hfill \\ y\hfill & =\hfill & \sum _{n=0}^{15}{B}_n{(\xi -N\mathrm{\Delta }\xi )}^n\hfill \\ z\hfill & =\hfill & \sum _{n=0}^{15}{C}_n{(\xi -N\mathrm{\Delta }\xi )}^n\hfill \end{array}$(6) with Δξ = ΩΔt = 0.38π. The coefficients A₀, A₁, B₀, B₁, C₀ and C₁ are obtained from the initial conditions for N = 0, then by imposing the continuity of the position and the velocity for the other steps. The other coefficients are given by recursion relations.

3 Simulation of the trap's stability diagram

The truncated series solution of the ion's equation of motion can be used to simulate the first stability domain for a radiofrequency quadrupole trap. For that we considered the evolution of the position of 200 ions of mass 1 amu up to 10,000 periods of the RF field (ξ_max = 2 ×10⁴π) in a trap having r₀ = 7 mm and z₀ = 5 mm. The ions were first generated inside the trap volume with uniform random positions and Maxwellian velocities with the temperature 1000 K. They were considered individually and the trajectory of each one of them was calculated before considering the next one. To be trapped, the coordinates x, y and z must inside the volume of the trap which has hyperboloidal electrodes. The trapping conditions are then

(7) $r^2-2z^2<r_0^2\text{and}2z^2-r^2<2z_0^2$(7)

This is tested every time step. If the test is negative, the ion is considered as lost and the calculations stopped for it. At ξ = ξ_max the number of ions remaining trapped for a working point (q_z, a_z) is counted.

The number of ions trapped up to ξ_max as function of the Mathieu parameters is shown in Fig. 1 in grayscale map. q_z was scanned from 0 to 1.5 with a step of 0.0111 and a_z taken from -0.5 to 0.2 with a step of 0.0044. The limits of the trapping domain obtained here correspond to those calculated using the recursion formula for the determination of β_z and β_r [6]. Fig. 1(a) corresponds to an ideal trap with f = 0 and Fig. 1(b) is obtained with f = 0.005. The main difference between the 2 graphs is the appearance of lines in the domain with reduced number of trapped ions. These are called the non linear resonances and occur when [3]

(8) $n_r{\beta }_r+n_z{\beta }_z=2n$(8) n_r, n_z and n are integers such that |n_r| + |n_z| is the minimum order of the potential inducing these resonances (here 4). In Fig. 1(b), we identify the lines 4β_z = 2, 4β_r = 2 and 2β_z + 2β_r = 2. They have been observed experimentally [11] when H⁺ ions were stored in a radiofrequency quadrupole ion trap having the same r₀ and z₀ we considered.

Fig. 1 Simulated lowest stability domain for (a) an ideal quadrupole trap and (b) a quadrupole trap with superimposed octopolar potential. The crosses represent the calculated limits of the domain and the dots are the calculated non linear resonance lines.

4 Ion's oscillation frequencies

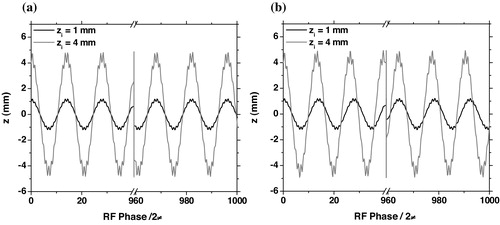
For the ideal trap, the ion's oscillation frequencies are only function of the Mathieu parameters a_z and q_z [6]. When the octopolar potential is present, the frequencies are also function of its strength (function of f) and of the amplitudes of the oscillations [5]. To see this effect using our simulation method, we studied the motion of an ion in the z-direction. We considered an ion starting from rest at t = 0 and z = z_i. We took a_z = 0 and different small values for q_z and f. The calculations were done up to 1000 periods of the RF voltage (ξ_max = 2 ×10³π). Fig. 2 give the results for q_z = 0.2, and z_i = 1 and 4 mm. Fig. 2(a) is obtained for f = 0 and Fig. 2(b) is for f = 0.05. As expected the oscillation frequencies are the same for the first case while they are different for the second. The frequency is larger for larger values of the amplitude. In all cases, we can estimate the fundamental frequency and its corresponding amplitude by fitting the curves using a sine function.

Fig. 2 Evolution of z as function of ξ for z_i = 1 and 4 mm. (a) f = 0%, (b) f = 5%

In order to calculate the frequencies for the cases we treated, we consider the ion's equation of motion (3)(3) $\frac{d^{2}u}{d{\tau }^2}+(a_u-2q_u\cos (2\tau )){\mathrm{ug}}_u(r,z)=0$(3) for z and with a_z = 0. This is

(9) $\frac{d^{2}z}{d{\tau }^2}-2q_{z}cos(2\tau )(z+\alpha z^3)=0$(9) with $\alpha =2f/r_0^2$.

The general solution is [5]

(10) $z=\sum _{n=-\infty }^{+\infty }{c}_{2n}cos(\beta +2n)\tau$(10) c_2n are constants. By considering only the terms for n = 0, 1 and −1, we can write

(11) $z=Acos\beta \tau +Bcos(\beta +2)\tau +Ccos(\beta -2)\tau$(11)

We suppose that A is much larger than B and C. Then

(12) $\frac{d^{2}z}{d{\tau }^2}=-{\beta }^{2}Acos\beta \tau -{(\beta +2)}^{2}Bcos(\beta +2)\tau -{(\beta -2)}^{2}Ccos(\beta -2)\tau$(12)

Neglecting the terms with B², B³, C², C³, BC, and keeping only the terms with cos βτ, cos(β + 2)τ and cos(β − 2)τ we get

(13) $\begin{array}{ccc}{z}^{3}cos(2\tau )\hfill & \approx \hfill & A^3{cos}^3\beta \tau +3A^2{cos}^2\beta \tau (Bcos(\beta +2)\tau +Ccos(\beta -2)\tau )\hfill \\ \hfill & \approx \hfill & \frac{9A^2}{8}\left(B+C\right)cos\beta \tau +\frac{3A^3}{8}cos(\beta +2)\tau +\frac{3A^3}{8}cos(\beta -2)\tau \hfill \end{array}$(13) (14) $zcos(2\tau )\approx \frac{B+C}{2}cos\beta \tau +\frac{A}{2}cos(\beta +2)\tau +\frac{A}{2}cos(\beta -2)\tau$(14)

Replacing (12)(12) $\frac{d^{2}z}{d{\tau }^2}=-{\beta }^{2}Acos\beta \tau -{(\beta +2)}^{2}Bcos(\beta +2)\tau -{(\beta -2)}^{2}Ccos(\beta -2)\tau$(12) –(14)(14) $zcos(2\tau )\approx \frac{B+C}{2}cos\beta \tau +\frac{A}{2}cos(\beta +2)\tau +\frac{A}{2}cos(\beta -2)\tau$(14) in Eq. (9)(9) $\frac{d^{2}z}{d{\tau }^2}-2q_{z}cos(2\tau )(z+\alpha z^3)=0$(9) We have

(15) $\left[{\beta }^{2}A+q_z\left(1+\frac{9}{4}\alpha A^2\right)(B+C)\right]cos\beta \tau +\left[{(\beta +2)}^{2}B+q_{z}A\left(1+\frac{3}{4}\alpha A^2\right)\right]cos(\beta +2)\tau +\left[{(\beta -2)}^{2}C+q_{z}A\left(1+\frac{3}{4}\alpha A^2\right)\right]cos(\beta -2)\tau =0$(15)

This gives

(16) ${\beta }^{2}A+q_z\left(1+\frac{9}{4}\alpha A^2\right)(B+C)=0$(16) (17) ${(\beta +2)}^{2}B+q_{z}A\left(1+\frac{3}{4}\alpha A^2\right)=0$(17) (18) ${(\beta -2)}^{2}C+q_{z}A\left(1+\frac{3}{4}\alpha A^2\right)=0$(18)

The initial condition gives the equation

(19) $A+B+C=z_i$(19)

For small values of β, Eqs. (17)(17) ${(\beta +2)}^{2}B+q_{z}A\left(1+\frac{3}{4}\alpha A^2\right)=0$(17) and (18)(18) ${(\beta -2)}^{2}C+q_{z}A\left(1+\frac{3}{4}\alpha A^2\right)=0$(18) give

(20) $B\approx -\frac{q_z}{4}A(1-\beta )\left(1+\frac{3}{4}\alpha A^2\right)$(20) (21) $C\approx -\frac{q_z}{4}A(1+\beta )\left(1+\frac{3}{4}\alpha A^2\right)$(21)

Eqs. (19)(19) $A+B+C=z_i$(19) –(21)(21) $C\approx -\frac{q_z}{4}A(1+\beta )\left(1+\frac{3}{4}\alpha A^2\right)$(21) then give

(22) $\frac{3}{8}{q}_z\alpha A^3-\left(1-\frac{q_z}{2}\right)A+z_i=0$(22)

Neglecting the term $\frac{3}{8}{q}_z\alpha A^3$, we find

(23) $A\approx \frac{z_i}{1-\frac{q_z}{2}}$(23)

This equation with Eqs. (16)(16) ${\beta }^{2}A+q_z\left(1+\frac{9}{4}\alpha A^2\right)(B+C)=0$(16) and (19)(19) $A+B+C=z_i$(19) give

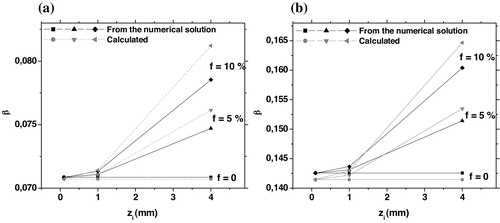
(24) ${\beta }^2=\frac{q_z^2}{2}\left(1+\frac{9}{4}\alpha A^2\right)$(24) Which reduces to the expression of the adiabatic approximatiopn for f = 0 [6]. In Fig. 3, we show the values of beta that we get from the truncated series solution of the equation of motion and those obtained using Eqs. (23)(23) $A\approx \frac{z_i}{1-\frac{q_z}{2}}$(23) and (24)(24) ${\beta }^2=\frac{q_z^2}{2}\left(1+\frac{9}{4}\alpha A^2\right)$(24) . We considered z_i = 0.1, 1 and 4 mm. For each one of these values, we took f = 0%, 5% and 10%. Fig. 3(a) is for q_z = 0.1 and Fig. 3(b) for q_z = 0.2. There is a good agreement between the simulation and the calculation. We have 3.4% difference in the worst case.

Fig. 3 Values of β obtained from the numerical solution and by the calculation. (a) q_z = 0.1, (b) q_z = 0.2

5 Conclusion

The equations of motion of ions in a radiofrequency quadrupole ion trap are solved numerically by representing the coordinates of the ions by truncated series of degree 15 and using recursion relations for the coefficients of the series. By considering the evolution of the position of hundreds of ions up to several thousands of periods of the RF field and counting the number of ions which remain in the geometrical limits of the trap, the stability diagram is obtained for an ideal trap and when an octopolar potential is added. The non linear resonances are observed. The calculations are possible thanks to the reduced computational time the method allows.

The method shows the variation of the ion's oscillation frequencies with the amplitude when the octopolar potential is present. For small value of the Mathieu parameter q_z, these variations are in good agreement with what is expected from the theory.

Acknowledgements

The present work has been accomplished under the project No. 09-ADV826-07 funded by KACST (King Abdul Aziz City for Science and Technology) through the Long Term Comprehensive National Plan for Science, Technology and Innovation program in Saudi Arabia.

Notes

Peer review under responsibility of Taibah University.