A Worked out Galois Group for the Classroom

Abstract

Let $f=X^6-3X^2-1\in Q[X]$ and let $L_f$ be the splitting field of f over $Q$. We show by hand that the Galois group $\text{Gal}(L_f/Q)$ of the Galois extension $L_f/Q$ is isomorphic to the alternating group A₄. Moreover, we show that the six roots of f correspond to the six edges of a tetrahedron and that the four roots of the polynomial $X^4+18X^2-72X+81$ correspond to the four faces of a tetrahedron, which allows us to determine all eight proper intermediate fields of the extension $L_f/Q$.

MSC:

• 11R32
• 11R16
• 11R11

1 Introduction

Teaching Galois theory, one often has the problem that the Galois group of a field extension of $Q$ is either quite simple or too difficult to be computed by hand. An example of a Galois group which is isomorphic to the dihedral group of order 8 can be found in Stewart [1, Ch. 13]. Introducing this example, Stewart writes that this Galois group has an “archetypal quality, since a simpler example would be too small to illustrate the theory adequately, and anything more complicated would be unwieldy” [1, p. 155]. Moreover, it is usually rather tedious to compute the Galois group along with the intermediate fields and their relations.

The aim of this note is to provide a worked out field extension over $Q$ whose Galois group is isomorphic to the alternating group A₄ (i.e., to the symmetry group of the tetrahedron), and to compute by hand all intermediate fields and their relations. If we do not require that the ground field is $Q$, a canonical way to obtain a field extension L/K with $\text{Gal}(L/K)\cong A_4$ for some fields $\mathit{\text{L⊋K⊋Q}}$, is to start with a polynomial $f\in Q[X]$ of degree 4 such that the Galois group of the field extension $L/Q$—where L is the splitting field of f over $Q$—is isomorphic to the symmetry group S₄. Then, since $A_4⊴S_4$, by the Galois correspondence we find a quadratic extension K of $Q$ such that $\text{Gal}(L/K)\cong A_4$ (see also Osofsky [2, p.222]). However, since the ground field K of the field extension L/K is already a field extension of $Q$, it is quite exhausting to compute $\text{Gal}(L/K)$ and the intermediate fields of L/K by hand.

Before we present our example in the next section, we set up the terminology (according to [1, 3]), where we assume that the reader is familiar with the basic facts of Galois theory with respect to field extensions over $Q$.

If $f\in Q[X]$ is a polynomial, then the smallest subfield of $C$ containing all of the roots of f is called the splitting field of f over $Q$. The splitting field of f over $Q$ is unique up to isomorphism. If $L/Q$ is a field extension and $Q\subseteq M\subseteq L$ is a field, then M is called an intermediate field of $L/Q$. If $M\subseteq L$ are fields, then the group of all automorphisms of L which fix M point-wise is the Galois group of the field extension L/M, denoted $\text{Gal}(L/M)$. Let $f\in Q[X]$ be a polynomial, $L_f$ its splitting field over $Q$, and M an intermediate subfield, so $Q\subseteq M\subseteq L_f$. Let $g\in M[X]$ and let $K_g\subseteq L_f$ be its splitting field over M. Then $K_g/M$ is a Galois extension. We will only consider Galois extensions of this type.

Now we can state the main theorem of Galois theory.

The Galois Correspondence. Let $L/Q$ be an arbitrary Galois extension. Then the following holds:

• To each subgroup $H⩽ \text{Gal}(L/Q)$ there exists an intermediate field L^H, such that

  $L^H=\{a\in L:\forall \sigma \in H(\sigma (a)=a)\}.$

• For each intermediate field $Q\subseteq M\subseteq L$ we have $\text{Gal}(L/M)⩽ \text{Gal}(L/Q)$ and

  $L^{\text{Gal}(L/M)}=M.$

• Let M₁ and M₂ be intermediate fields of some field extension $L/Q$, and let $H_1:=\text{Gal}(L/M_1)$. If, for some $\sigma \in \text{Gal}(L/Q)$, we have $\text{Gal}(L/M_2)=\sigma H_1{\sigma }^{-1}$, then the fields M₁ and M₂ are conjugate.

• If $Q\subseteq M\subseteq L$ is such that $\text{Gal}(L/M)$ is a normal subgroup of $\text{Gal}(L/Q)$ (i.e., the conjugate class of M contains only M), then the field extension $M/Q$ is Galois and

  $\text{Gal}(M/Q)\cong \text{Gal}(L/Q)/\text{Gal}(L/M).$

2 A field extension $\mathit{L/}Q$ with $\text{Gal}(\mathit{L/}Q)\cong {\mathit{A}}_{\mathit{4}}$

We start with the polynomial $f=X^6-3X^2-1$ and consider its splitting field $L_f$ over $Q$. The goal is to show that $\text{Gal}(L_f/Q)\cong A_4$, where A₄ is the alternating group of degree 4, which is isomorphic to the symmetry group of the tetrahedron.

In order to compute the roots of f, we replace X² by ξ and first compute the roots of the irreducible polynomial $g={\xi }^3-3\xi -1$. To see that g is irreducible, consider the polynomial $$\tilde{g}:={(\xi -2)}^3-3(\xi -2)-1={\xi }^3-6{\xi }^2+9\xi -3.$$

By the Eisenstein-Schönemann Criterion (with p = 3), we see that $\tilde{g}$ is irreducible over $Q$, and so is g.

Observe that every complex number $\xi \ne 0$ can be written as $\xi =\alpha +\beta$ with ${\alpha }^3+{\beta }^3=1$. Indeed, for $\beta =\xi -\alpha$ we have ${\beta }^3={\xi }^3-3{\xi }^2\alpha +3\xi {\alpha }^2-{\alpha }^3$ and hence $$1={\alpha }^3+{\beta }^3=\xi ({\xi }^2-3\xi \alpha +3{\alpha }^2).$$

This is a quadratic equation for $\alpha \in C$ with a solution if $\xi \ne 0$. In particular, a root ξ of g can be written in the form $\xi =\alpha +\beta$ with ${\alpha }^3+{\beta }^3=1$. Then $$g={(\alpha +\beta )}^3-3(\alpha +\beta )-1={\alpha }^3+3{\alpha }^2\beta +3\alpha {\beta }^3+{\beta }^3-3\alpha -3\beta -1=0.$$

So, since ${\alpha }^3+{\beta }^3=1$, we have $$3\alpha \beta (\alpha +\beta )-3(\alpha +\beta )=0$$and since $\alpha +\beta \ne 0$, we obtain $$\alpha \beta =1,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\beta =\frac{1}{\alpha },\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\text{and}\hspace{1em}{\alpha }^3+\frac{1}{{\alpha }^3}=1.$$

If we set $z:={\alpha }^3$, then $z+\frac{1}{z}=1$ and hence $z^2-z+1=0$. We choose the solution $$z_1=\frac{1}{2}+i\frac{\sqrt{3}}{2}=e^{\pi i/3}.$$

Now α is a third root of z₁ and we choose $\alpha =e^{\pi i/9}$. Since $\beta =\frac{1}{\alpha }=\overline{\alpha }$, we obtain $${\xi }_1:=\xi =\alpha +\overline{\alpha }=2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(\pi /9).$$

Then $${\xi }_1^3={(\alpha +\overline{\alpha })}^3={\alpha }^3+3\underset{=\alpha }{\underset{}{\underbrace{{\alpha }^2 \overline{\alpha }}}}+3\underset{=\overline{\alpha }}{\underset{}{\underbrace{\alpha {\overline{\alpha }}^2}}}+{\overline{\alpha }}^3=3(\underset{={\xi }_1}{\underset{}{\underbrace{\alpha +\overline{\alpha }}}})+\underset{=1}{\underset{}{\underbrace{{\alpha }^3+{\overline{\alpha }}^3}}}=3 {\xi }_1+1$$which shows that ξ₁ is indeed a root of $g={\xi }^3-3\xi -1$. The two remaining third roots of z₁ are $$\begin{array}{ccccc}{e}^{2\pi i/3}·e^{\pi i/9}& =& e^{7\pi i/9}& =& {\alpha }^7,\\ e^{4\pi i/3}·e^{\pi i/9}& =& e^{13\pi i/9}& =& {\alpha }^{13}.\end{array}$$

Hence the roots of g are given by $$\begin{array}{ccccc}{\xi }_1& =& \alpha +\overline{\alpha }& =& 2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(\pi /9),\\ {\xi }_2& =& {\alpha }^7+{\overline{\alpha }}^7& =& 2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(7\pi /9),\\ {\xi }_3& =& {\alpha }^{13}+{\overline{\alpha }}^{13}& =& 2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(13\pi /9).\end{array}$$

Thus, $g={\xi }^3-3\xi -1=(\xi -{\xi }_1)(\xi -{\xi }_2)(\xi -{\xi }_3)$, which shows that ${\xi }_1 {\xi }_2 {\xi }_3=1$, ${\xi }_1 {\xi }_2+{\xi }_2 {\xi }_3+{\xi }_3 {\xi }_1=-3$, and ${\xi }_1+{\xi }_2+{\xi }_3=0$.

Notice that $$-{\xi }_2=e^{\pi i}(e^{7\pi i/9}+e^{-7\pi i/9})=e^{16\pi i/9}+e^{2\pi i/9}=e^{-2\pi i/9}+e^{2\pi i/9}={\alpha }^2+{\overline{\alpha }}^2,$$

and similarly we have $-{\xi }_3={\alpha }^4+{\overline{\alpha }}^4$. Thus we have $$2-{\xi }_1^2=2-{(\alpha +\overline{\alpha })}^2=2-(2\underset{=1}{\underset{}{\underbrace{\alpha \overline{\alpha }}}}+\underset{=-{\xi }_2}{\underset{}{\underbrace{{\alpha }^2+{\overline{\alpha }}^2}}})=2-(2-{\xi }_2)={\xi }_2.$$

Similarly we get $2-{\xi }_2^2={\xi }_3$ and $2-{\xi }_3^2={\xi }_1$. This shows that $Q({\xi }_1)=Q({\xi }_2)=Q({\xi }_3)$. In particular, $Q({\xi }_1)$ is the splitting field of g over $Q$. So, for $L_g:=Q({\xi }_1)$, the field extension $L_g/Q$ is Galois.

For convenience in later arguments, we rewrite the three roots of g as follows: $$\begin{array}{c}{\xi }_1=\alpha +\overline{\alpha }=2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(\pi /9)\\ {\xi }_2=2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(7\pi /9)=-2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(7\pi /9+\pi )=-2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(2\pi /9)\\ {\xi }_3=2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(13\pi /9)=-2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(13\pi /9+\pi )=-2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(4\pi /9).\end{array}$$

Then by construction we obtain the six pairwise distinct roots of f as $\pm \sqrt{{\xi }_k}$ for $1\le k\le 3$. In particular, we define $$\begin{array}{ccccccc}{\zeta }_1& :=& \sqrt{2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(\pi /9)}& \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}& {\zeta }_4& :=& -{\zeta }_1\\ {\zeta }_2& :=& i\sqrt{2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(2\pi /9)}& \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}& {\zeta }_5& :=& -{\zeta }_2\\ {\zeta }_3& :=& i\sqrt{2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(4\pi /9)}& \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}& {\zeta }_6& :=& -{\zeta }_3.\end{array}$$

This shows that $$f=(X-{\zeta }_1)(X+{\zeta }_1)(X-{\zeta }_2)(X+{\zeta }_2)(X-{\zeta }_3)(X+{\zeta }_3).$$

Notice that since ${\xi }_1 {\xi }_2 {\xi }_3=1$, we have ${\zeta }_1^2 {\zeta }_2^2 {\zeta }_3^2=1$, which implies that the product $(\pm {\zeta }_1)(\pm {\zeta }_2)(\pm {\zeta }_3)=\pm 1$. Moreover, by definition of ${\zeta }_1,{\zeta }_2,{\zeta }_3$ we have ${\zeta }_1 {\zeta }_2 {\zeta }_3=-1$.

Now, let us show that f is irreducible over $Q$. For this, assume on the contrary that $f=p·q$ for some nonconstant polynomials $p,q\in Q[X]$. If $\mathrm{\text{deg}}(p)=1$, e.g., $p=(X-{\zeta }_1)$, then ${\zeta }_1\in Q$, which is obviously a contradiction. Assume now that $\mathrm{\text{deg}}(p)=2$, e.g., $p=(X-{\zeta }_1)(X+{\zeta }_1)=X^2-{\xi }_1$ or $p=(X-{\zeta }_1)(X-{\zeta }_2)=X^2-({\zeta }_1+{\zeta }_2)X+{\zeta }_1 {\zeta }_2$. Then, in the former case this would imply ${\xi }_1\in Q$, and in the latter case this would imply ${\zeta }_1 {\zeta }_2=-\frac{1}{{\zeta }_3}\in Q$. Thus in both cases we arrive at a contradiction. If $\mathrm{\text{deg}}(p)=3$ and p is of the form $$p=(X-{\zeta }_1)(X+{\zeta }_1)(X-{\zeta }_2)=X^3-{\zeta }_2{X}^2+\dots ,$$then ${\zeta }_2\in Q$, which is again a contradiction. Finally, if $\mathrm{\text{deg}}(p)=3$ and p is of the form $$p=(X-{\zeta }_1)(X-{\zeta }_2)(X-{\zeta }_3)=1+\mathit{\text{bX}}+c{X}^2+X^3,$$

then q is of the form $$q=(X+{\zeta }_1)(X+{\zeta }_2)(X+{\zeta }_3)=-1+\mathit{\text{bX}}-c{X}^2+X^3.$$

Since $f=p·q=X^6-3X^2-1$, we must have $2b-c^2=0$ and $b^2-2c=-3$. In particular, $b=\frac{c^2}{2}$ and therefore $\frac{c^4}{4}-2c+3=0$, but since $\frac{c^4}{4}-2c+3>1$ for all $c\in R$, we conclude that $p\notin Q[X]$. Thus, there are no nonconstant polynomials $p,q\in Q[X]$ such that $f=p·q$, which shows that f is irreducible over $Q$. In particular, since $f\in Q[X]$ is a monic, irreducible polynomial of degree 6 with the six roots ${\zeta }_1,\dots ,{\zeta }_6$, we have ${\zeta }_m\notin Q({\xi }_k)$ for $1\le m\le 6$ and $1\le k\le 3$.

Let $G_f:=\text{Gal}(L_f/Q)$ and $G_g:=\text{Gal}(L_g/Q)$, where $L_f$ and L_g are the splitting fields of f and g, respectively. Then, since $\mathrm{\text{deg}}(g)=3$ and $L_g=Q({\xi }_1)$, we have $\left|G_g\right|=3$ and therefore $G_g\cong C_3$, where C_n denotes the cyclic group of order n. Furthermore, since the field extension $L_g/Q$ is Galois, $\text{Gal}(L_f/L_g)⊴G_f$ and $G_f/\text{Gal}(L_f/L_g)\cong C_3$. Since ${\zeta }_m\notin Q({\xi }_k)$, $\text{Gal}(L_f/L_g)$ is not the trivial group.

Now, we consider $\text{Gal}(L_f/L_g)$. Let $\sigma \in \text{Gal}(L_f/L_g)$. Then $\sigma ({\xi }_k)={\xi }_k$ for $1\le k\le 3$. Thus $\sigma ({\zeta }_m)=\pm {\zeta }_m$ for all $1\le m\le 6$. To see this, consider, for example, ${\xi }_1=\sigma ({\xi }_1)=\sigma ({\zeta }_1·{\zeta }_1)=\sigma ({\zeta }_1)·\sigma ({\zeta }_1)$. Therefore $\text{Gal}(L_f/L_g)⩽C_2\times C_2\times C_2$.

If we adjoin to the field L_g a root ζ_m (for $1\le m\le 6$), then we obtain the intermediate field $L_g⊊L_g({\zeta }_m)\subseteq L_f$, where $\text{Gal}(L_g({\zeta }_m)/L_g)\cong C_2$. Since ${\zeta }_m^2={\xi }_k$ for some $1\le k\le 3$ and $Q({\xi }_1)=Q({\xi }_2)=Q({\xi }_3)$, we have $L_g({\zeta }_m)=Q({\zeta }_m)$. Since each of the fields $Q({\zeta }_k)$ (for $1\le k\le 3$) is the splitting field of a quadratic polynomial of the form $Z^2-{\zeta }_k^2$ for $1\le k\le 3$, each of the field extensions $Q({\zeta }_k)/L_g$ (for $1\le k\le 3$) is Galois with $\text{Gal}(Q({\zeta }_k)/L_g)\cong C_2$.

Now, there are three possible intermediate fields of the form $Q({\zeta }_m)$, namely $Q({\zeta }_1),Q({\zeta }_2)$, and $Q({\zeta }_3)$. To see that these three intermediate fields are pairwise distinct, notice first that, since ${\zeta }_1=\sqrt{2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}(\phi )}\in R$, we have $Q({\zeta }_1)\subseteq R$, and therefore ${\zeta }_2,{\zeta }_3\notin Q({\zeta }_1)$. Furthermore, if ${\zeta }_1\in Q({\zeta }_2)$, then, since $\mathfrak{R}({\zeta }_2)=0$, we can write $${\zeta }_1=a+b {\zeta }_2^2+c {\zeta }_2^4=a+b {\xi }_2+c {\xi }_2^2\hspace{1em}\text{with}a,b,c\in Q.$$

Thus, ${\zeta }_1\in Q({\xi }_2)$, which is not the case. Similarly, ${\zeta }_1\notin Q({\xi }_3)$. Furthermore, if ${\zeta }_2\in Q({\zeta }_3)$, then with ${\zeta }_2 {\zeta }_3=\frac{1}{{\zeta }_1}$ we would have ${\zeta }_1\in Q({\zeta }_3)$, which is not the case.

To summarize, for $1\le k\le 3$ we have $L_g({\zeta }_k)⊊L_f, \text{Gal}(L_g({\zeta }_k)/L_g)\cong C_2$, and from $\text{Gal}(L_f/L_g)⩽C_2\times C_2\times C_2$ we obtain that $C_2\times C_2⩽\text{Gal}(L_f/L_g)$. In particular we have that $\text{Gal}(L_f/Q)$ is not cyclic.

Finally, we show that $L_f=Q({\zeta }_i,{\zeta }_j)$ for any distinct i and j with $1\le i,j\le 3$. To see this, recall that $(\pm {\zeta }_1)(\pm {\zeta }_2)(\pm {\zeta }_3)=\pm 1$, which implies that we can compute, for example, ζ₂ from ζ₁ and ζ₃. Now, since $Q({\zeta }_i^2)=Q({\xi }_i)$, which implies ${\xi }_i\in Q({\zeta }_i)$, and since $Q({\xi }_i)=Q({\xi }_j)$ for all $1\le i,j\le 3$, we conclude that ${\xi }_j\in Q({\zeta }_i)$ for all $1\le i,j\le 3$. Furthermore, since ζ_j is a root of $Z^2-{\xi }_j\in Q({\zeta }_i)[Z]$ and ${\zeta }_j\notin Q({\zeta }_i)$, we have $\text{Gal}(L_f/Q({\zeta }_i))\cong C_2$. In particular, $\text{Gal}(L_f/L_g)\cong C_2\times C_2$.

Now, we are ready to show that $\text{Gal}(L_f/Q)\cong A_4$. Since $L_f=Q({\zeta }_1,\dots ,{\zeta }_6)$, every element $\pi \in \text{Gal}(L_f/Q)$ corresponds to a permutation of ${\zeta }_1,\dots ,{\zeta }_6$, where the elements ${\xi }_1,{\xi }_2,{\xi }_3$ (i.e., the elements ${\zeta }_1^2,{\zeta }_2^2,{\zeta }_3^2$) are permuted cyclically. By the observations above, every $\pi \in \text{Gal}(L_f/Q)$ can be written as $\pi ={\sigma }_l^m°{\rho }^n$ for $l\in \{1,2,3\}$, $m\in \{0,1\}$, and $n\in \{0,1,2\}$, where, in cycle notation, $$\rho =({\zeta }_1 {\zeta }_2 {\zeta }_3)({\zeta }_4 {\zeta }_5 {\zeta }_6),$$and for $1\le j\le 6$, $${\sigma }_l({\zeta }_j)=\{\begin{array}{cc}{\zeta }_j\hfill & \text{if}j\in \{l,l+3\},\hfill \\ -{\zeta }_j\hfill & \text{otherwise}.\hfill \end{array}$$

Since ρ corresponds to a cyclic permutation of ${\xi }_1,{\xi }_2,{\xi }_3$, we have $\rho \in \text{Gal}(L_g/Q)$, and since for $1\le i\le 3$ we have ${\sigma }_l({\xi }_i)={\xi }_i,{\sigma }_l\in \text{Gal}(L_f/L_g)$. So, since $\text{Gal}(L_f/L_g)\cong C_2\times C_2$, we get that for any pairwise distinct $i,j,k\in \{1,2,3\}$, if ${\sigma }_l({\zeta }_i)=-{\zeta }_i$ and ${\sigma }_l({\zeta }_j)=-{\zeta }_j$, then ${\sigma }_l({\zeta }_k)={\zeta }_k$ (i.e., l = k), which corresponds to the fact that ${\zeta }_k=\frac{-1}{{}^{}{\zeta }_i·{\zeta }_j}$.

Let us now consider a tetrahedron T with the six edges ①, ②, ③, ④, ⑤, ⑥, where the pairs of edges (①, ④), (②, ⑤), and (③, ⑥) are opposite edges of T. If we identify the six edges ①, …, ⑥ with the six roots ${\zeta }_1,\dots ,{\zeta }_6$ of f, then every element $\pi \in \text{Gal}(L_f/Q)$ corresponds to an element of the symmetry group of the tetrahedron T, i.e., to an element of the alternating group A₄ (this fact is visualized by Figure 3 at the end of the next section).

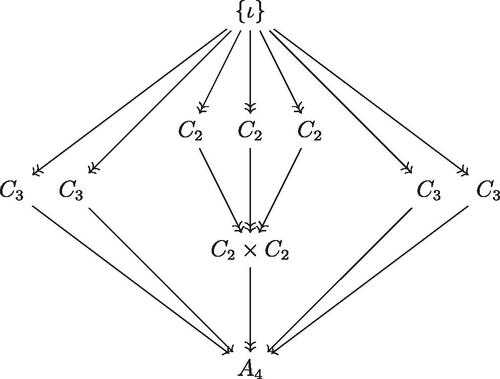
3 Subgroups and Intermediate Fields

Figure 1 illustrates all subgroups of A₄. For some of these subgroups of A₄, we already found the corresponding intermediate fields. In particular, we found that the field that corresponds to $C_2\times C_2$ is $L_g=Q({\xi }_1)$, and since $C_2\times C_2$ is a normal subgroup of A₄, we obtain that $\text{Gal}(L_g/Q)\cong A_4/(C_2\times C_2)\cong C_3$. Furthermore, the three fields which correspond to the subgroups C₂ are $Q({\zeta }_1),Q({\zeta }_2)$, and $Q({\zeta }_3)$. Notice that these three fields are pairwise conjugate. To see this, let $\sigma \in \text{Gal}(L_f/Q({\zeta }_1))$ and let, for example, $\pi \in \text{Gal}(L_f/Q)$ be such that $\pi ({\zeta }_1)=-{\zeta }_2$, $\pi ({\zeta }_2)=-{\zeta }_3,\pi ({\zeta }_3)={\zeta }_1$. Then $$\pi °\sigma °{\pi }^{-1}({\zeta }_2)=\pi °\sigma (-{\zeta }_1)=\pi (-{\zeta }_1)={\zeta }_2,$$which shows that the automorphism $\pi °\sigma °{\pi }^{-1}$ fixes ζ₂, i.e., $\pi °\sigma °{\pi }^{-1}$ is an element of $\text{Gal}(L_f/Q({\zeta }_2))$.

Fig. 1 Subgroup Diagram of $\text{Gal}(L_f/Q)\cong A_4$. For two groups H and G, an arrow $H\to G$ or $H\twoheadrightarrow G$ indicates that H is a subgroup or a normal subgroup of G; and ι denotes the identity automorphism of $L_f$.

In order to find the four intermediate fields M_i (for $1\le i\le 4$) with $\text{Gal}(L_f/M_i)\cong C_3$, we proceed as follows. First, we identify ${\zeta }_1,\dots ,{\zeta }_6$ with the numbers $1,\dots ,6$ and the elements of the group A₄ with a subgroup of S₆ (i.e., the symmetry group of $\{1,\dots ,6\}$). Furthermore, let, again in cycle notation, $$\begin{array}{c}{H}_1:=〈(123)(456)〉,\hspace{1em}{H}_2:=〈(156)(423)〉,\\ H_3:=〈(345)(612)〉,\hspace{1em}{H}_4:=〈(264)(531)〉,\end{array}$$be the four subgroups of A₄ which are isomorphic to C₃. Then, the four intermediate fields M_i are the four fixed-fields $$M_i:=L_f^{H_i}=\{a\in L_f:\forall \sigma \in H_i,\sigma (a)=a\}.$$

Let ${\vartheta }_1,{\vartheta }_2,{\vartheta }_3,{\vartheta }_4$, be defined as follows: $$\begin{array}{ccccccc}{\vartheta }_1& :=& {\xi }_1({\zeta }_2+{\zeta }_6)& +& {\xi }_2({\zeta }_3+{\zeta }_4)& +& {\xi }_3({\zeta }_1+{\zeta }_5)\\ {\vartheta }_2& :=& {\xi }_1({\zeta }_5+{\zeta }_3)& +& {\xi }_2({\zeta }_6+{\zeta }_4)& +& {\xi }_3({\zeta }_1+{\zeta }_2)\\ {\vartheta }_3& :=& {\xi }_1({\zeta }_5+{\zeta }_6)& +& {\xi }_2({\zeta }_3+{\zeta }_1)& +& {\xi }_3({\zeta }_4+{\zeta }_2)\\ {\vartheta }_4& :=& {\xi }_1({\zeta }_2+{\zeta }_3)& +& {\xi }_2({\zeta }_6+{\zeta }_1)& +& {\xi }_3({\zeta }_4+{\zeta }_5).\end{array}$$

It is not hard to verify that for each $1\le i\le 4,M_i=Q({\vartheta }_i)$. For example, consider the element $\sigma :=(132)(465)={((123)(456))}^2\in H_1$. Then $$\sigma ({\vartheta }_1)={\xi }_3({\zeta }_1+{\zeta }_5)+{\xi }_1({\zeta }_2+{\zeta }_6)+{\xi }_2({\zeta }_3+{\zeta }_4)={\vartheta }_1$$which shows that $\sigma \in \text{Gal}(L_f/M_1)$. Furthermore, we can verify that for $${\sigma }_2:=(25)(36),\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\sigma }_3:=(14)(25),\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\sigma }_4:=(14)(36),$$

we have $$L_f^{{\sigma }_2{H}_1{\sigma }_2^{-1}}=M_2,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{L}_f^{{\sigma }_3{H}_1{\sigma }_3^{-1}}=M_3,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{L}_f^{{\sigma }_4{H}_1{\sigma }_4^{-1}}=M_4,$$

which shows that the four intermediate fields $M_1,\dots ,M_4$ are pairwise conjugate. For example, let $\tau :=(132)(465)\in H_1$. Then $\pi :={\sigma }_2°\tau °{\sigma }_2^{-1}=(165)(243)$ and we have $$\pi ({\vartheta }_2)={\xi }_3({\zeta }_1+{\zeta }_2)+{\xi }_1({\zeta }_5+{\zeta }_3)+{\xi }_2({\zeta }_6+{\zeta }_4)={\vartheta }_2$$which shows that $\pi \in \text{Gal}(L_f/M_2)$. Moreover, we get that $$\begin{array}{c}\pi ({\vartheta }_1)={\xi }_3({\zeta }_4+{\zeta }_5)+{\xi }_1({\zeta }_2+{\zeta }_3)+{\xi }_2({\zeta }_6+{\zeta }_1)={\vartheta }_4,\\ \pi ({\vartheta }_4)={\xi }_3({\zeta }_4+{\zeta }_2)+{\xi }_1({\zeta }_5+{\zeta }_6)+{\xi }_2({\zeta }_3+{\zeta }_1)={\vartheta }_3,\\ \pi ({\vartheta }_3)={\xi }_3({\zeta }_1+{\zeta }_5)+{\xi }_1({\zeta }_2+{\zeta }_6)+{\xi }_2({\zeta }_3+{\zeta }_4)={\vartheta }_1,\end{array}$$ which shows that π is a cyclic permutation of ${\vartheta }_1,{\vartheta }_4$, and ${\vartheta }_3$.

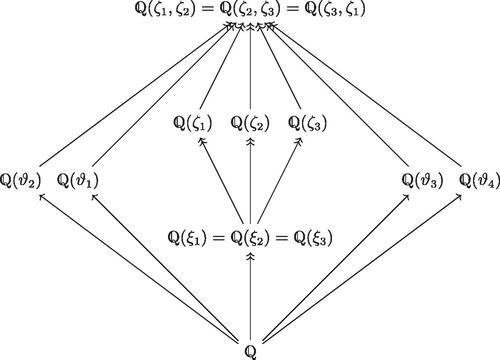
Figure 2 illustrates all intermediate fields of the field extension $L_f/Q$.

Fig. 2 Diagram of intermediate fields. For two fields K and M, an arrow $K\to M$ or $K\twoheadrightarrow M$ indicates that K is a subfield of M, and $K\twoheadrightarrow M$ indicates that the field extension is Galois.

Finally, we consider the polynomial $h:=(X-{\vartheta }_1)(X-{\vartheta }_2)(X-{\vartheta }_3)(X-{\vartheta }_4)$. To keep the notation short, we introduce the following function: For integers a, b we define $a(\text{Mod} b)$ by stipulating $b(\text{Mod} b):=b$ and $a(\text{Mod} b):=a(\text{Mod} b)$ for $a\ne b$. Then, since for $1\le j\le 6$, ${\zeta }_j=-{\zeta }_{j+3(\text{mod}\mathrm{ }6)}$ and ${\zeta }_j^2={\xi }_{j(\text{mod}\mathrm{ }3)}$, and bearing in mind the identities $$\begin{array}{c}{\zeta }_1·{\zeta }_2·{\zeta }_3=1,{\xi }_1·{\xi }_2·{\xi }_3=1,\\ {\xi }_1+{\xi }_2+{\xi }_3=0,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\xi }_1^2·{\xi }_2^2+{\xi }_1^2·{\xi }_3^2+{\xi }_2^2·{\xi }_3^2=9,\end{array}$$and for $1\le i\le 3$, $$\begin{array}{c}{\xi }_i^2+{\xi }_{i+1(\text{Mod}\mathrm{ }3)}^2=4+{\xi }_i,\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\xi }_i^2=2-{\xi }_{i+1(\text{Mod}\mathrm{ }3)},\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\xi }_i^3=3{\xi }_i+1,\\ {\xi }_i^4({\xi }_{i+1(\text{Mod}\mathrm{ }3)}^2+{\xi }_{i+2(\text{Mod}\mathrm{ }3)}^2)=17-9{\xi }_{i+1(\text{Mod}\mathrm{ }3)},\end{array}$$

we obtain $$h=X^4+18X^2-72X+81.$$

Since ${\vartheta }_1,\dots ,{\vartheta }_4$ belong to L_h, where L_h is the splitting field of $h\in Q[X]$ over $Q$, L_h is a subfield of L_f, and since $L_h/Q$ is a Galois extension, $\text{Gal}(L_f/L_h)⊴A_4$ and therefore $\text{Gal}(L_h/Q)\cong A_4/\text{Gal}(L_f/L_h)$, which implies that $\text{Gal}(L_h/Q)$ is isomorphic to either $\left\{\iota \right\}$, C₃, or A₄. We have seen above that there is a $\pi \in \text{Gal}(L_h/Q)$ which is a cyclic permutation of ${\vartheta }_1,{\vartheta }_3,{\vartheta }_4$, and similarly, we find a $\pi \prime \in \text{Gal}(L_h/Q)$ which is a cyclic permutation of ${\vartheta }_2,{\vartheta }_3,{\vartheta }_4$. Hence $\text{Gal}(L_h/Q)$ must be isomorphic to A₄. In particular, the fields $L_f$ and L_h are isomorphic.

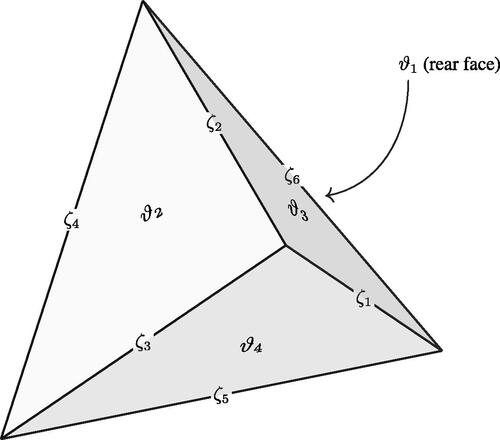
Let us consider again the tetrahedron T with the six edges ${\zeta }_1,\dots ,{\zeta }_6$, where the pairs of edges ${\zeta }_i,{\zeta }_{i+3}$ (for $1\le i\le 3$) are opposite edges of T. We already know that the group $\text{Gal}(L_f/Q)$ is isomorphic to the symmetry group of the tetrahedron acting on its six edges. We show now that $\text{Gal}(L_h/Q)$ is isomorphic to the symmetry group of the tetrahedron acting on its four faces. For this, we identify the four faces of the tetrahedron with the four roots ${\vartheta }_1,\dots ,{\vartheta }_4$ of h as illustrated in Figure 3.

Fig. 3 The elements of $\text{Gal}(L_f/Q)$ and $\text{Gal}(L_h/Q)$ act as congruence transformations of the tetrahedron on its edges and faces, respectively.

In order to see that the elements of the symmetry group of the tetrahedron correspond simultaneously to the elements of $\text{Gal}(L_f/Q)$ and $\text{Gal}(L_h/Q)$, respectively, we consider two elements of the symmetry group of the tetrahedron.

First, let ρ₁ be the rotation by the angle π about the axis joining the midpoints of the edges ζ₁ and ζ₄. Then ρ₁ acts on the edges and the faces of the tetrahedron as follows: $${\zeta }_1\to {\zeta }_1\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\zeta }_4\to {\zeta }_4{\zeta }_3\leftrightarrow {\zeta }_6\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\zeta }_2\leftrightarrow {\zeta }_5$$

and $$\begin{array}{c}\underset{{\vartheta }_1}{\underset{}{\underbrace{{\xi }_1({\zeta }_2+{\zeta }_6)+{\xi }_2({\zeta }_3+{\zeta }_4)+{\xi }_3({\zeta }_1+{\zeta }_5)}}}\leftrightarrow \underset{{\vartheta }_2}{\underset{}{\underbrace{{\xi }_1({\zeta }_5+{\zeta }_3)+{\xi }_2({\zeta }_6+{\zeta }_4)+{\xi }_3({\zeta }_1+{\zeta }_2)}}}\\ \underset{{\vartheta }_3}{\underset{}{\underbrace{{\xi }_1({\zeta }_5+{\zeta }_6)+{\xi }_2({\zeta }_3+{\zeta }_1)+{\xi }_3({\zeta }_4+{\zeta }_2)}}}\leftrightarrow \underset{{\vartheta }_4}{\underset{}{\underbrace{{\xi }_1({\zeta }_2+{\zeta }_3)+{\xi }_2({\zeta }_6+{\zeta }_1)+{\xi }_3({\zeta }_4+{\zeta }_5)}}}.\end{array}$$

Notice that the intermediate field which corresponds to ρ₁ is $Q({\zeta }_1)$.

Second, let ρ₂ be the rotation by the angle $2\pi /3$ about the axis joining the center of the face ${\vartheta }_1$ with the opposite vertex. Then ρ₂ acts on the edges and the faces of the tetrahedron as follows: $${\zeta }_1\to {\zeta }_2\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\zeta }_2\to {\zeta }_3\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\zeta }_3\to {\zeta }_1{\zeta }_4\to {\zeta }_5\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\zeta }_5\to {\zeta }_6\mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{\zeta }_6\to {\zeta }_4$$and $$\begin{array}{c}\underset{{\vartheta }_1}{\underset{}{\underbrace{{\xi }_1({\zeta }_2+{\zeta }_6)+{\xi }_2({\zeta }_3+{\zeta }_4)+{\xi }_3({\zeta }_1+{\zeta }_5)}}}\to \underset{{\vartheta }_1}{\underset{}{\underbrace{{\xi }_2({\zeta }_3+{\zeta }_4)+{\xi }_3({\zeta }_1+{\zeta }_5)+{\xi }_1({\zeta }_2+{\zeta }_6)}}}\\ \underset{{\vartheta }_2}{\underset{}{\underbrace{{\xi }_1({\zeta }_5+{\zeta }_3)+{\xi }_2({\zeta }_6+{\zeta }_4)+{\xi }_3({\zeta }_1+{\zeta }_2)}}}\to \underset{{\vartheta }_4}{\underset{}{\underbrace{{\xi }_2({\zeta }_6+{\zeta }_1)+{\xi }_3({\zeta }_4+{\zeta }_5)+{\xi }_1({\zeta }_2+{\zeta }_3)}}}\\ \underset{{\vartheta }_4}{\underset{}{\underbrace{{\xi }_1({\zeta }_2+{\zeta }_3)+{\xi }_2({\zeta }_6+{\zeta }_1)+{\xi }_3({\zeta }_4+{\zeta }_5)}}}\to \underset{{\vartheta }_3}{\underset{}{\underbrace{{\xi }_2({\zeta }_3+{\zeta }_1)+{\xi }_3({\zeta }_4+{\zeta }_2)+{\xi }_1({\zeta }_5+{\zeta }_6)}}}\\ \underset{{\vartheta }_3}{\underset{}{\underbrace{{\xi }_1({\zeta }_5+{\zeta }_6)+{\xi }_2({\zeta }_3+{\zeta }_1)+{\xi }_3({\zeta }_4+{\zeta }_2)}}}\to \underset{{\vartheta }_2}{\underset{}{\underbrace{{\xi }_2({\zeta }_6+{\zeta }_4)+{\xi }_3({\zeta }_1+{\zeta }_2)+{\xi }_1({\zeta }_5+{\zeta }_3)}}}.\end{array}$$

Notice that the intermediate field which corresponds to ρ₂ is $Q({\vartheta }_1)$.

Conclusion

What we have achieved is a visualization of a Galois group in terms of the edges and faces of a tetrahedron. In particular, we found two polynomials f and h of degree six and four, respectively, such that the roots of f correspond to the six edges and the roots of h correspond to the to the four faces (or vertices) of the tetrahedron. Moreover, since we were able to carry out all the calculations by hand, we obtained a complete understanding of the field extension $L_f/Q$, and in addition, we have an illustrative example of a Galois extension that shows the power and beauty of Galois theory.

Acknowledgment

We would like to thank the referees for their valuable remarks and comments.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Notes on contributors

Lorenz Halbeisen

LORENZ HALBEISEN received his Ph.D. in mathematics from ETH Zürich in 1994. He has been a lecturer at Queen’s University Belfast and at the University of Zürich, and since 2022 he is professor at the ETH Zürich. He likes all kinds of puzzles and mathematical problems with a combinatorial flavor.

Department of Mathematics, ETH Zentrum, Rämistrasse 101, 8092 Zürich, Switzerland

[email protected]

Norbert Hungerbühler

NORBERT HUNGERBÜHLER received his Ph.D. in mathematics from ETH Zürich in 1994. He has been a professor at UAB in Birmingham, Alabama, at the University of Fribourg, and since 2010 at ETH Zürich. He likes to combine different areas of mathematics and to look at familiar things from a new viewpoint.

Department of Mathematics, ETH Zentrum, Rämistrasse 101, 8092 Zürich, Switzerland

[email protected]