The inverse electromagnetic scattering problem by a penetrable cylinder at oblique incidence

ABSTRACT

In this work, we consider the method of non-linear boundary integral equation for solving numerically the inverse scattering problem of obliquely incident electromagnetic waves by a penetrable homogeneous cylinder in three dimensions. We consider the indirect method and simple representations for the electric and the magnetic fields in order to derive a system of five integral equations, four on the boundary of the cylinder and one on the unit circle where we measure the far-field pattern of the scattered wave. We solve the system iteratively by linearizing only the far-field equation. Numerical results illustrate the feasibility of the proposed scheme.

KEYWORDS:

• Inverse electromagnetic scattering
• oblique incidence
• non-linear integral equation method

AMS SUBJECT CLASSIFICATIONS:

• 35R30
• 45E05
• 45G15
• 65N21
• 65R32

1. Introduction

The inverse obstacle scattering problem is to image the scattering object, i.e. find its shape and location, from the knowledge of the far-field pattern of the scattered wave. The medium is illuminated by light at given direction and polarization. Then, Maxwell’s equations are used to model the propagation of the light through the medium, see [1,2] for an overview. This problem is of great interest because of its applications in many areas of physics and engineering (non-destructive testing, biomedical imaging, remote sensing, and target identification). We refer to [3–7] for some recent applications.

Due to the complexity of the combined system of equations for the electric and the magnetic fields, it is common to impose additional assumptions on the incident illumination and the nature of the scatterer. We consider time-harmonic incident electromagnetic plane wave that due to the linearity of the problem will result to a time-independent system of equations. In addition, the penetrable object is considered as an infinitely long homogeneous cylinder. Then, it is characterized by constant permittivity and permeability. The problem is further simplified if we impose normal incidence for the incident wave. However, in this work, we consider the more complicated case of oblique incidence.

The three-dimensional scattering problem modeled by Maxwell’s equations is then equivalent to a pair of two-dimensional Helmholtz equations for two scalar fields (the third components of the electric and the magnetic fields). This approach reduces the difficulty of the problem but results to more complicated boundary conditions. The transmission conditions now contain also the tangential derivatives of the electric and magnetic fields. In [8], we showed that the corresponding direct problem is well-posed and we constructed a unique solution using the direct integral equation method. A similar problem has been considered for an impedance cylinder embedded in a homogeneous [9] and in an inhomogeneous medium [10]. Different numerical solutions of the direct problem have been also proposed using finite difference/element methods [11,12], the Galerkin method [13], the Nyström method [14], the Green’s tensor method [15], the method of auxiliary sources [16,17], the generalized Debye method [18], and the separation of variables method [19–21].

On the other hand, the inverse problem is non-linear and ill-posed. The non-linearity is due to the dependence of the solution of the scattering problem on the unknown boundary curve. The smoothness of the mapping from the boundary to the far-field pattern reflects the ill-posedness of the inverse problem. The unique solvability of the inverse problem is still an open problem. The first and only, to our knowledge, uniqueness result was presented recently in [22] for the case of an impedance cylinder using the Lax–Phillips method.

In this work, we solve the inverse problem by formulating an equivalent system of non-linear integral equations that is solved using a regularized iterative scheme. This method was introduced by Kress and Rundell [23] and then considered in many different problems, in acoustic scattering problems [24,25], in elasticity [26,27] and in electrical impedance problem [28]. Our iterative scheme is based on the idea of Johansson and Sleeman [29] first applied to the inverse acoustic scattering problem for a sound soft object. See [26,30], for applications of the method in different problems. We assume integral representations for the solutions that result to a system consisting of four integral equations on the unknown boundary (considering the transmission conditions) and one on the unit circle (taking into account the asymptotic expansion of the solutions). In our case, compared to [29,30] where only smooth and weakly singular integral operators are present in the systems of equations, appears also a singular operator (the tangential derivative of the single layer) due to the much more involved transmission conditions.

We solve the system of equations in two steps. First, given an initial guess for the boundary curve, we solve the well-posed subsystem (equations on the boundary) to obtain the corresponding densities and then we solve the linearized (with respect to the boundary) ill-posed far-field equation to update the initial approximation of the radial function. We consider Tikhonov regularization and the normal equations are solved by the conjugate gradient method. To improve the reconstructions, we take also into account measurements for few incident waves.

This work can be seen as a first step for solving the problem in the more complicated anisotropic case. There, one has to treat the three-dimensional problem differently and the integral equation method will result to a more complicated system of equations. The simplification due to the symmetry of the problem is also questionable and the unique solvability even for the direct problem is still an open problem. We refer to [31] for a numerical solution using a subspace-based optimization method.

The paper is organized as follows: in Section 2, we present the direct scattering problem, the elastic potentials, and the equivalent system of integral equations that provide us with the far-field data. The inverse problem is stated in Section 3, where we construct an equivalent system of integral equation using the indirect integral equation method. In Section 4, the two-step method for the parametrized form of the system and the necessary Fréchet derivative of the integral operators are presented. The numerical examples give satisfactory results and justify the applicability of the proposed iterative scheme.

2. The direct problem

We consider the scattering of an electromagnetic wave by a penetrable cylinder in $R^3$. Let $\mathbf{x}=(x,y,z)\in R^3.$ We denote by ${\mathrm{\Omega }}_{\mathit{int}}=\{\mathbf{x}:(x,y)\in \mathrm{\Omega },z\in R\}$ the cylinder, where $\mathrm{\Omega }$ is a bounded domain in $R^2$ with smooth boundary $\mathrm{\Gamma }.$ The cylinder ${\mathrm{\Omega }}_{\mathit{int}}$ is oriented parallel to the z-axis and $\mathrm{\Omega }$ is its horizontal cross section. We assume constant permittivity ${\mathit{ϵ}}_0$ and permeability ${\mathit{\mu }}_0$ for the exterior domain ${\mathrm{\Omega }}_{\mathit{ext}}:=R^3\backslash {\overline{\mathrm{\Omega }}}_{\mathit{int}}.$ The interior domain ${\mathrm{\Omega }}_{\mathit{int}}$ is also characterized by constant parameters ${\mathit{ϵ}}_1$ and ${\mathit{\mu }}_1.$

We define the exterior magnetic ${\mathbf{H}}^{\mathit{ext}}(\mathbf{x},t)$ and electric field ${\mathbf{E}}^{\mathit{ext}}(\mathbf{x},t)$ for $\mathbf{x}\in {\mathrm{\Omega }}_{\mathit{ext}},t\in R$ and the interior fields ${\mathbf{H}}^{\mathit{int}}(\mathbf{x},t)$ and ${\mathbf{E}}^{\mathit{int}}(\mathbf{x},t)$ for $\mathbf{x}\in {\mathrm{\Omega }}_{\mathit{int}},t\in R,$ that satisfy the Maxwell’s equations(1) $$\begin{array}{c}\hfill \begin{array}{ccccc}\hfill \mathrm{\nabla }\times {\mathbf{E}}^{\mathit{ext}}+{\mathit{\mu }}_0\frac{\mathit{\partial }{\mathbf{H}}^{\mathit{ext}}}{\mathit{\partial }t}& =0,\hfill & \hfill \mathrm{\nabla }\times {\mathbf{H}}^{\mathit{ext}}-{\mathit{ϵ}}_0\frac{\mathit{\partial }{\mathbf{E}}^{\mathit{ext}}}{\mathit{\partial }t}& =0,\hfill & \mathbf{x}\in {\mathrm{\Omega }}_{\mathit{ext}},\\ \hfill \mathrm{\nabla }\times {\mathbf{E}}^{\mathit{int}}+{\mathit{\mu }}_1\frac{\mathit{\partial }{\mathbf{H}}^{\mathit{int}}}{\mathit{\partial }t}& =0,\hfill & \hfill \mathrm{\nabla }\times {\mathbf{H}}^{\mathit{int}}-{\mathit{ϵ}}_1\frac{\mathit{\partial }{\mathbf{E}}^{\mathit{int}}}{\mathit{\partial }t}& =0,\hfill & \mathbf{x}\in {\mathrm{\Omega }}_{\mathit{int}}.\end{array}\end{array}$$(1)

and the transmission conditions(2) $$\begin{array}{c}\hfill \widehat{\mathit{n}}\times {\mathbf{E}}^{\mathit{int}}=\widehat{\mathit{n}}\times {\mathbf{E}}^{\mathit{ext}},\widehat{\mathit{n}}\times {\mathbf{H}}^{\mathit{int}}=\widehat{\mathit{n}}\times {\mathbf{H}}^{\mathit{ext}},\mathbf{x}\in \mathrm{\Gamma },\end{array}$$(2)

where $\widehat{\mathit{n}}$ is the outward normal vector, directed into ${\mathrm{\Omega }}_{\mathit{ext}}$.

We illuminate the cylinder with an incident electromagnetic plane wave at oblique incidence, meaning transverse magnetic (TM) polarized wave. We define by $\mathit{\theta }$ the incident angle with respect to the negative z axis and by $\mathit{\varphi }$ the polar angle of the incident direction $\widehat{\mathit{d}}$ (in spherical coordinates), see Figure 1. Then, $\widehat{\mathit{d}}=(sin\mathit{\theta }cos\mathit{\varphi },sin\mathit{\theta }sin\mathit{\varphi },-cos\mathit{\theta })$ and the polarization vector is given by $\widehat{\mathit{p}}=(cos\mathit{\theta }cos\mathit{\varphi },cos\mathit{\theta }sin\mathit{\varphi },sin\mathit{\theta }),$ satisfying $\widehat{\mathit{d}}\perp \widehat{\mathit{p}},$ for $\mathit{\theta }\in (0,\mathit{\pi }).$ The upcoming analysis can also be carried out to the case of transverse electric polarized incident plane wave.

Figure 1. The geometry of the scattering problem.

In the following, due to the linearity of the problem, we suppress the time-dependence of the fields and because of the cylindrical symmetry of the medium we express the incident fields as separable functions of $\mathit{x}:=(x,y)$ and z.

Let $\mathit{\omega }>0$ be the frequency and $k_0=\mathit{\omega }\sqrt{{\mathit{\mu }}_0{\mathit{ϵ}}_0}$ the wave number in ${\mathrm{\Omega }}_{\mathit{ext}}$. We define $\mathit{\beta }=k_{0}cos\mathit{\theta }$ and ${\mathit{\kappa }}_0=\sqrt{k_0^2-{\mathit{\beta }}^2}=k_{0}sin\mathit{\theta }$ and it follows that the incident fields can be decomposed to [8](3) $$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathbf{E}}^{\mathit{inc}}(\mathbf{x};\widehat{\mathit{d}},\widehat{\mathit{p}})={\mathbf{e}}^{\mathit{inc}}(\mathit{x})e^{-i\mathit{\beta }z},{\mathbf{H}}^{\mathit{inc}}(\mathbf{x};\widehat{\mathit{d}},\widehat{\mathit{p}})={\mathbf{h}}^{\mathit{inc}}(\mathit{x})e^{-i\mathit{\beta }z},\end{array}\end{array}$$(3)

where$$\begin{array}{cc}\hfill {\mathbf{e}}^{\mathit{inc}}(\mathit{x})& =\frac{1}{\sqrt{{\mathit{ϵ}}_0}}\widehat{\mathit{p}}{e}^{i{\mathit{\kappa }}_0(xcos\mathit{\varphi }+ysin\mathit{\varphi })},\hfill \\ \hfill {\mathbf{h}}^{\mathit{inc}}(\mathit{x})& =\frac{1}{\sqrt{{\mathit{\mu }}_0}}(sin\mathit{\varphi },-cos\mathit{\varphi },0)e^{i{\mathit{\kappa }}_0(xcos\mathit{\varphi }+ysin\mathit{\varphi })}.\hfill \end{array}$$

After some calculations, we can reformulate Maxwell’s euqations (1(1) $$\begin{array}{c}\hfill \begin{array}{ccccc}\hfill \mathrm{\nabla }\times {\mathbf{E}}^{\mathit{ext}}+{\mathit{\mu }}_0\frac{\mathit{\partial }{\mathbf{H}}^{\mathit{ext}}}{\mathit{\partial }t}& =0,\hfill & \hfill \mathrm{\nabla }\times {\mathbf{H}}^{\mathit{ext}}-{\mathit{ϵ}}_0\frac{\mathit{\partial }{\mathbf{E}}^{\mathit{ext}}}{\mathit{\partial }t}& =0,\hfill & \mathbf{x}\in {\mathrm{\Omega }}_{\mathit{ext}},\\ \hfill \mathrm{\nabla }\times {\mathbf{E}}^{\mathit{int}}+{\mathit{\mu }}_1\frac{\mathit{\partial }{\mathbf{H}}^{\mathit{int}}}{\mathit{\partial }t}& =0,\hfill & \hfill \mathrm{\nabla }\times {\mathbf{H}}^{\mathit{int}}-{\mathit{ϵ}}_1\frac{\mathit{\partial }{\mathbf{E}}^{\mathit{int}}}{\mathit{\partial }t}& =0,\hfill & \mathbf{x}\in {\mathrm{\Omega }}_{\mathit{int}}.\end{array}\end{array}$$(1) ) as a system of equations only for the z-component of the electric and magnetic fields [8]. The interior fields $e_3^{\mathit{int}}(\mathit{x})$ and $h_3^{\mathit{int}}(\mathit{x}),\mathit{x}\in {\mathrm{\Omega }}_1:=\mathrm{\Omega }$ and the exterior fields $e_3^{\mathit{ext}}(\mathit{x})$ and $h_3^{\mathit{ext}}(\mathit{x}),$ $\mathit{x}\in {\mathrm{\Omega }}_0:=R^2\backslash \mathrm{\Omega }$ satisfy the Helmholtz equations(4) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{\Delta }{e}_3^{\mathit{int}}+{\mathit{\kappa }}_1^2{e}_3^{\mathit{int}}=0,\mathrm{\Delta }{h}_3^{\mathit{int}}+{\mathit{\kappa }}_1^2{h}_3^{\mathit{int}}=0,\mathit{x}& \in {\mathrm{\Omega }}_1,\hfill \\ \hfill \mathrm{\Delta }{e}_3^{\mathit{ext}}+{\mathit{\kappa }}_0^2{e}_3^{\mathit{ext}}=0,\mathrm{\Delta }{h}_3^{\mathit{ext}}+{\mathit{\kappa }}_0^2{h}_3^{\mathit{ext}}=0,\mathit{x}& \in {\mathrm{\Omega }}_0,\hfill \end{array}\end{array}$$(4)

where ${\mathit{\kappa }}_1^2={\mathit{\mu }}_1{\mathit{ϵ}}_1{\mathit{\omega }}^2-{\mathit{\beta }}^2.$ Here, we assume ${\mathit{\mu }}_1{\mathit{ϵ}}_1>{\mathit{\mu }}_0{\mathit{ϵ}}_0{cos}^2\mathit{\theta }$ in order to have ${\mathit{\kappa }}_1^2>0.$

The transmission conditions (2(2) $$\begin{array}{c}\hfill \widehat{\mathit{n}}\times {\mathbf{E}}^{\mathit{int}}=\widehat{\mathit{n}}\times {\mathbf{E}}^{\mathit{ext}},\widehat{\mathit{n}}\times {\mathbf{H}}^{\mathit{int}}=\widehat{\mathit{n}}\times {\mathbf{H}}^{\mathit{ext}},\mathbf{x}\in \mathrm{\Gamma },\end{array}$$(2) ) can also be written only for the z-component of the fields. Let $(\widehat{\mathit{n}},\widehat{\mathit{\tau }})$ be a local coordinate system, where $\widehat{\mathit{n}}=(n_1,n_2)$ is the outward normal vector and $\widehat{\mathit{\tau }}=(-n_2,n_1)$ the outward tangent vector on $\mathrm{\Gamma }.$ We define $\frac{\mathit{\partial }}{\mathit{\partial }n}=\widehat{\mathit{n}}·{\mathrm{\nabla }}_t,$ $\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\tau }}=\widehat{\mathit{\tau }}·{\mathrm{\nabla }}_t,$ where ${\mathrm{\nabla }}_t={\mathbf{e}}_1\frac{\mathit{\partial }}{\mathit{\partial }x}+{\mathbf{e}}_2\frac{\mathit{\partial }}{\mathit{\partial }y}$ and ${\mathbf{e}}_1,{\mathbf{e}}_2$ denote the unit vectors in $R^2.$ Then, we rewrite the boundary conditions as [8](5) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill e_3^{\mathit{int}}& =e_3^{\mathit{ext}},\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\\ \hfill {\tilde{\mathit{\mu }}}_1\mathit{\omega }\frac{\mathit{\partial }{h}_3^{\mathit{int}}}{\mathit{\partial }n}+{\mathit{\beta }}_1\frac{\mathit{\partial }{e}_3^{\mathit{int}}}{\mathit{\partial }\mathit{\tau }}& ={\tilde{\mathit{\mu }}}_0\mathit{\omega }\frac{\mathit{\partial }{h}_3^{\mathit{ext}}}{\mathit{\partial }n}+{\mathit{\beta }}_0\frac{\mathit{\partial }{e}_3^{\mathit{ext}}}{\mathit{\partial }\mathit{\tau }},\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\\ \hfill h_3^{\mathit{int}}& =h_3^{\mathit{ext}},\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\\ \hfill {\widetilde{\mathit{ϵ}}}_1\mathit{\omega }\frac{\mathit{\partial }{e}_3^{\mathit{int}}}{\mathit{\partial }n}-{\mathit{\beta }}_1\frac{\mathit{\partial }{h}_3^{\mathit{int}}}{\mathit{\partial }\mathit{\tau }}& ={\widetilde{\mathit{ϵ}}}_0\mathit{\omega }\frac{\mathit{\partial }{e}_3^{\mathit{ext}}}{\mathit{\partial }n}-{\mathit{\beta }}_0\frac{\mathit{\partial }{h}_3^{\mathit{ext}}}{\mathit{\partial }\mathit{\tau }},\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\end{array}\end{array}$$(5)

where ${\tilde{\mathit{\mu }}}_j={\mathit{\mu }}_j/{\mathit{\kappa }}_j^2,{\widetilde{\mathit{ϵ}}}_j={\mathit{ϵ}}_j/{\mathit{\kappa }}_j^2,{\mathit{\beta }}_j=\mathit{\beta }/{\mathit{\kappa }}_j^2,$ for $j=0,1.$ The exterior fields are decomposed to $e_3^{\mathit{ext}}=e_3^{\mathit{sc}}+e_3^{\mathit{inc}}$ and $h_3^{\mathit{ext}}=h_3^{\mathit{sc}}+h_3^{\mathit{inc}},$ where $e_3^{\mathit{sc}}$ and $h_3^{\mathit{sc}}$ denote the scattered electric and magnetic field, respectively. From (3(3) $$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathbf{E}}^{\mathit{inc}}(\mathbf{x};\widehat{\mathit{d}},\widehat{\mathit{p}})={\mathbf{e}}^{\mathit{inc}}(\mathit{x})e^{-i\mathit{\beta }z},{\mathbf{H}}^{\mathit{inc}}(\mathbf{x};\widehat{\mathit{d}},\widehat{\mathit{p}})={\mathbf{h}}^{\mathit{inc}}(\mathit{x})e^{-i\mathit{\beta }z},\end{array}\end{array}$$(3) ), we see that(6) $$\begin{array}{c}\hfill \begin{array}{c}\hfill e_3^{\mathit{inc}}(\mathit{x})=\frac{1}{\sqrt{{\mathit{ϵ}}_0}}sin\mathit{\theta }{e}^{i{\mathit{\kappa }}_0(xcos\mathit{\varphi }+ysin\mathit{\varphi })},h_3^{\mathit{inc}}(\mathit{x})=0.\end{array}\end{array}$$(6)

To ensure that the scattered fields are outgoing, we impose in addition the radiation conditions in $R^2:$ (7) $$\begin{array}{c}\hfill \begin{array}{c}\hfill \underset{r\to \infty }{lim}\sqrt{r}\left(\frac{\mathit{\partial }{e}_3^{\mathit{sc}}}{\mathit{\partial }r}-i{\mathit{\kappa }}_0{e}_3^{\mathit{sc}}\right)=0,\underset{r\to \infty }{lim}\sqrt{r}\left(\frac{\mathit{\partial }{h}_3^{\mathit{sc}}}{\mathit{\partial }r}-i{\mathit{\kappa }}_0{h}_3^{\mathit{sc}}\right)=0,\\ \hfill \end{array}\end{array}$$(7)

where $r=|\mathit{x}|,$ uniformly over all directions.

Now we are in position to formulate the direct transmission problem for oblique incident wave: find the fields $h_3^{\mathit{int}},h_3^{\mathit{sc}},e_3^{\mathit{int}}$, and $e_3^{\mathit{sc}}$ that satisfy the Helmholtz equations (4(4) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{\Delta }{e}_3^{\mathit{int}}+{\mathit{\kappa }}_1^2{e}_3^{\mathit{int}}=0,\mathrm{\Delta }{h}_3^{\mathit{int}}+{\mathit{\kappa }}_1^2{h}_3^{\mathit{int}}=0,\mathit{x}& \in {\mathrm{\Omega }}_1,\hfill \\ \hfill \mathrm{\Delta }{e}_3^{\mathit{ext}}+{\mathit{\kappa }}_0^2{e}_3^{\mathit{ext}}=0,\mathrm{\Delta }{h}_3^{\mathit{ext}}+{\mathit{\kappa }}_0^2{h}_3^{\mathit{ext}}=0,\mathit{x}& \in {\mathrm{\Omega }}_0,\hfill \end{array}\end{array}$$(4) ), the transmission conditions (5(5) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill e_3^{\mathit{int}}& =e_3^{\mathit{ext}},\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\\ \hfill {\tilde{\mathit{\mu }}}_1\mathit{\omega }\frac{\mathit{\partial }{h}_3^{\mathit{int}}}{\mathit{\partial }n}+{\mathit{\beta }}_1\frac{\mathit{\partial }{e}_3^{\mathit{int}}}{\mathit{\partial }\mathit{\tau }}& ={\tilde{\mathit{\mu }}}_0\mathit{\omega }\frac{\mathit{\partial }{h}_3^{\mathit{ext}}}{\mathit{\partial }n}+{\mathit{\beta }}_0\frac{\mathit{\partial }{e}_3^{\mathit{ext}}}{\mathit{\partial }\mathit{\tau }},\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\\ \hfill h_3^{\mathit{int}}& =h_3^{\mathit{ext}},\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\\ \hfill {\widetilde{\mathit{ϵ}}}_1\mathit{\omega }\frac{\mathit{\partial }{e}_3^{\mathit{int}}}{\mathit{\partial }n}-{\mathit{\beta }}_1\frac{\mathit{\partial }{h}_3^{\mathit{int}}}{\mathit{\partial }\mathit{\tau }}& ={\widetilde{\mathit{ϵ}}}_0\mathit{\omega }\frac{\mathit{\partial }{e}_3^{\mathit{ext}}}{\mathit{\partial }n}-{\mathit{\beta }}_0\frac{\mathit{\partial }{h}_3^{\mathit{ext}}}{\mathit{\partial }\mathit{\tau }},\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\end{array}\end{array}$$(5) ) and the radiation conditions (7(7) $$\begin{array}{c}\hfill \begin{array}{c}\hfill \underset{r\to \infty }{lim}\sqrt{r}\left(\frac{\mathit{\partial }{e}_3^{\mathit{sc}}}{\mathit{\partial }r}-i{\mathit{\kappa }}_0{e}_3^{\mathit{sc}}\right)=0,\underset{r\to \infty }{lim}\sqrt{r}\left(\frac{\mathit{\partial }{h}_3^{\mathit{sc}}}{\mathit{\partial }r}-i{\mathit{\kappa }}_0{h}_3^{\mathit{sc}}\right)=0,\\ \hfill \end{array}\end{array}$$(7) ).

Theorem 2.1:

If ${\mathit{\kappa }}_1^2$ is not an interior Dirichlet eigenvalue and ${\mathit{\kappa }}_0^2$ is not an interior Dirichlet and Neumann eigenvalue, then the direct transmission problem (4(4) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{\Delta }{e}_3^{\mathit{int}}+{\mathit{\kappa }}_1^2{e}_3^{\mathit{int}}=0,\mathrm{\Delta }{h}_3^{\mathit{int}}+{\mathit{\kappa }}_1^2{h}_3^{\mathit{int}}=0,\mathit{x}& \in {\mathrm{\Omega }}_1,\hfill \\ \hfill \mathrm{\Delta }{e}_3^{\mathit{ext}}+{\mathit{\kappa }}_0^2{e}_3^{\mathit{ext}}=0,\mathrm{\Delta }{h}_3^{\mathit{ext}}+{\mathit{\kappa }}_0^2{h}_3^{\mathit{ext}}=0,\mathit{x}& \in {\mathrm{\Omega }}_0,\hfill \end{array}\end{array}$$(4) )–(7(7) $$\begin{array}{c}\hfill \begin{array}{c}\hfill \underset{r\to \infty }{lim}\sqrt{r}\left(\frac{\mathit{\partial }{e}_3^{\mathit{sc}}}{\mathit{\partial }r}-i{\mathit{\kappa }}_0{e}_3^{\mathit{sc}}\right)=0,\underset{r\to \infty }{lim}\sqrt{r}\left(\frac{\mathit{\partial }{h}_3^{\mathit{sc}}}{\mathit{\partial }r}-i{\mathit{\kappa }}_0{h}_3^{\mathit{sc}}\right)=0,\\ \hfill \end{array}\end{array}$$(7) ) admits a unique solution.

Proof The proof is based on the integral representation of the solution resulting to a Fredholm type system of boundary integral equations. For more details, see [8, Theorem 3.2].

In the following, $j=0,1$ counts for the exterior ($\mathit{x}\in {\mathrm{\Omega }}_0$) and interior domain ($\mathit{x}\in {\mathrm{\Omega }}_1$), respectively. We introduce the single- and double-layer potentials defined by:(8) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill ({\mathcal{S}}_{j}f)(\mathit{x})& ={\int }_{\mathrm{\Gamma }}{\mathrm{\Phi }}_j(\mathit{x},\mathit{y})f(\mathit{y})\mathrm{d}s(\mathit{y}),\hfill & \hfill \mathit{x}\in {\mathrm{\Omega }}_j,\\ \hfill ({\mathcal{D}}_{j}f)(\mathit{x})& ={\int }_{\mathrm{\Gamma }}\frac{\mathit{\partial }{\mathrm{\Phi }}_j}{\mathit{\partial }n(\mathit{y})}(\mathit{x},\mathit{y})f(\mathit{y})\mathrm{d}s(\mathit{y}),\hfill & \hfill \mathit{x}\in {\mathrm{\Omega }}_j,\end{array}\end{array}$$(8)

where ${\mathrm{\Phi }}_j$ is the fundamental solution of the Helmholtz equation in $R^2:$ (9) $$\begin{array}{c}\hfill {\mathrm{\Phi }}_j(\mathit{x},\mathit{y})=\frac{i}{4}{H}_0^{(1)}({\mathit{\kappa }}_j|\mathit{x}-\mathit{y}|),\mathit{x},\mathit{y}\in {\mathrm{\Omega }}_j,\mathit{x}\ne \mathit{y},\end{array}$$(9)

and $H_0^{(1)}$ is the Hankel function of the first kind and zero order. We define also the integral operators(10) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill (S_{j}f)(\mathit{x})& ={\int }_{\mathrm{\Gamma }}{\mathrm{\Phi }}_j(\mathit{x},\mathit{y})f(\mathit{y})\mathrm{d}s(\mathit{y}),\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\\ \hfill (D_{j}f)(\mathit{x})& ={\int }_{\mathrm{\Gamma }}\frac{\mathit{\partial }{\mathrm{\Phi }}_j}{\mathit{\partial }n(\mathit{y})}(\mathit{x},\mathit{y})f(\mathit{y})\mathrm{d}s(\mathit{y}),\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\\ \hfill (N{S}_{j}f)(\mathit{x})& ={\int }_{\mathrm{\Gamma }}\frac{\mathit{\partial }{\mathrm{\Phi }}_j}{\mathit{\partial }n(\mathit{x})}(\mathit{x},\mathit{y})f(\mathit{y})\mathrm{d}s(\mathit{y}),\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\\ \hfill (N{D}_{j}f)(\mathit{x})& ={\int }_{\mathrm{\Gamma }}\frac{{\mathit{\partial }}^2{\mathrm{\Phi }}_j}{\mathit{\partial }n(\mathit{x})\mathit{\partial }n(\mathit{y})}(\mathit{x},\mathit{y})f(\mathit{y})\mathrm{d}s(\mathit{y}),\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\\ \hfill (T{S}_{j}f)(\mathit{x})& ={\int }_{\mathrm{\Gamma }}\frac{\mathit{\partial }{\mathrm{\Phi }}_j}{\mathit{\partial }\mathit{\tau }(\mathit{x})}(\mathit{x},\mathit{y})f(\mathit{y})\mathrm{d}s(\mathit{y}),\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\\ \hfill (T{D}_{j}f)(\mathit{x})& ={\int }_{\mathrm{\Gamma }}\frac{{\mathit{\partial }}^2{\mathrm{\Phi }}_j}{\mathit{\partial }\mathit{\tau }(\mathit{x})\mathit{\partial }n(\mathit{y})}(\mathit{x},\mathit{y})f(\mathit{y})\mathrm{d}s(\mathit{y}),\hfill & \hfill \mathit{x}\in \mathrm{\Gamma }.\end{array}\end{array}$$(10)

The following theorem was proven in [8].

Theorem 2.2:

Let the assumptions of Theorem 2.1 still hold. Then, the potentials(11) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill e_3^{\mathit{int}}(\mathit{x})& =-({\mathcal{D}}_1{\mathit{\varphi }}_1)(\mathit{x})+({\mathcal{S}}_1{\mathit{\eta }}_1)(\mathit{x}),\hfill & \hfill \mathit{x}\in {\mathrm{\Omega }}_1,\\ \hfill h_3^{\mathit{int}}(\mathit{x})& =-({\mathcal{D}}_1{\mathit{\psi }}_1)(\mathit{x})+({\mathcal{S}}_1{\mathit{\xi }}_1)(\mathit{x}),\hfill & \hfill \mathit{x}\in {\mathrm{\Omega }}_1,\\ \hfill e_3^{\mathit{ext}}(\mathit{x})& =({\mathcal{D}}_0{\mathit{\varphi }}_0)(\mathit{x})-({\mathcal{S}}_0{\mathit{\eta }}_0)(\mathit{x}),\hfill & \hfill \mathit{x}\in {\mathrm{\Omega }}_0,\\ \hfill h_3^{\mathit{ext}}(\mathit{x})& =({\mathcal{D}}_0{\mathit{\psi }}_0)(\mathit{x})-({\mathcal{S}}_0{\mathit{\xi }}_0)(\mathit{x}),\hfill & \hfill \mathit{x}\in {\mathrm{\Omega }}_0,\end{array}\end{array}$$(11)

solve the direct transmission problem (4(4) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{\Delta }{e}_3^{\mathit{int}}+{\mathit{\kappa }}_1^2{e}_3^{\mathit{int}}=0,\mathrm{\Delta }{h}_3^{\mathit{int}}+{\mathit{\kappa }}_1^2{h}_3^{\mathit{int}}=0,\mathit{x}& \in {\mathrm{\Omega }}_1,\hfill \\ \hfill \mathrm{\Delta }{e}_3^{\mathit{ext}}+{\mathit{\kappa }}_0^2{e}_3^{\mathit{ext}}=0,\mathrm{\Delta }{h}_3^{\mathit{ext}}+{\mathit{\kappa }}_0^2{h}_3^{\mathit{ext}}=0,\mathit{x}& \in {\mathrm{\Omega }}_0,\hfill \end{array}\end{array}$$(4) )–(7(7) $$\begin{array}{c}\hfill \begin{array}{c}\hfill \underset{r\to \infty }{lim}\sqrt{r}\left(\frac{\mathit{\partial }{e}_3^{\mathit{sc}}}{\mathit{\partial }r}-i{\mathit{\kappa }}_0{e}_3^{\mathit{sc}}\right)=0,\underset{r\to \infty }{lim}\sqrt{r}\left(\frac{\mathit{\partial }{h}_3^{\mathit{sc}}}{\mathit{\partial }r}-i{\mathit{\kappa }}_0{h}_3^{\mathit{sc}}\right)=0,\\ \hfill \end{array}\end{array}$$(7) ) provided that the densities ${\mathit{\varphi }}_0\in H^{1/2}(\mathrm{\Gamma })$ and ${\mathit{\psi }}_0\in H^{1/2}(\mathrm{\Gamma })$ satisfy the system of integral equations(12) $$\begin{array}{c}\hfill ({\mathbf{D}}_0+{\mathbf{K}}_0)\left(\begin{array}{c}{\mathit{\varphi }}_0\\ {\mathit{\psi }}_0\end{array}\right)={\mathbf{b}}_0,\end{array}$$(12)

where$$\begin{array}{cc}\hfill {\mathbf{D}}_0& =\left(\begin{array}{cc}{D}_0-\frac{1}{2}I& 0\\ 0& D_0-\frac{1}{2}I\end{array}\right),\hfill \\ \hfill {\mathbf{K}}_0& =\left(\begin{array}{cc}-\frac{{\widetilde{\mathit{ϵ}}}_1}{{\widetilde{\mathit{ϵ}}}_0}{S}_0{K}_1& -\frac{1}{{\widetilde{\mathit{ϵ}}}_0\mathit{\omega }}{S}_0({\mathit{\beta }}_1{L}_1+{\mathit{\beta }}_0{L}_0)\\ \frac{1}{{\tilde{\mathit{\mu }}}_0\mathit{\omega }}{S}_0({\mathit{\beta }}_1{L}_1+{\mathit{\beta }}_0{L}_0)& -\frac{{\tilde{\mathit{\mu }}}_1}{{\tilde{\mathit{\mu }}}_0}{S}_0{K}_1\end{array}\right),\hfill \\ \hfill {\mathbf{b}}_0& =\left(\begin{array}{c}-S_0{\mathit{\partial }}_{\mathit{\eta }}+\frac{{\widetilde{\mathit{ϵ}}}_1}{{\widetilde{\mathit{ϵ}}}_0}{S}_0{K}_1\\ -\frac{1}{{\tilde{\mathit{\mu }}}_0\mathit{\omega }}{S}_0({\mathit{\beta }}_0{\mathit{\partial }}_{\mathit{\tau }}+{\mathit{\beta }}_1{L}_1)\end{array}\right)e_3^{\mathit{inc}},\hfill \end{array}$$

and $K_j:={\left(N{S}_j\pm \frac{1}{2}I\right)}^{-1}N{D}_j,L_j:=2(T{D}_j-T{S}_j{K}_j).$ The rest of the densities satisfy ${\mathit{\varphi }}_1={\mathit{\varphi }}_0+e_3^{\mathit{inc}},{\mathit{\psi }}_1={\mathit{\psi }}_0,{\mathit{\eta }}_j=K_j{\mathit{\varphi }}_j$ and ${\mathit{\xi }}_j=K_j{\mathit{\psi }}_j.$

The solutions $e_3^{\mathit{sc}}$ and $h_3^{\mathit{sc}}$ of (4(4) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{\Delta }{e}_3^{\mathit{int}}+{\mathit{\kappa }}_1^2{e}_3^{\mathit{int}}=0,\mathrm{\Delta }{h}_3^{\mathit{int}}+{\mathit{\kappa }}_1^2{h}_3^{\mathit{int}}=0,\mathit{x}& \in {\mathrm{\Omega }}_1,\hfill \\ \hfill \mathrm{\Delta }{e}_3^{\mathit{ext}}+{\mathit{\kappa }}_0^2{e}_3^{\mathit{ext}}=0,\mathrm{\Delta }{h}_3^{\mathit{ext}}+{\mathit{\kappa }}_0^2{h}_3^{\mathit{ext}}=0,\mathit{x}& \in {\mathrm{\Omega }}_0,\hfill \end{array}\end{array}$$(4) )–(7(7) $$\begin{array}{c}\hfill \begin{array}{c}\hfill \underset{r\to \infty }{lim}\sqrt{r}\left(\frac{\mathit{\partial }{e}_3^{\mathit{sc}}}{\mathit{\partial }r}-i{\mathit{\kappa }}_0{e}_3^{\mathit{sc}}\right)=0,\underset{r\to \infty }{lim}\sqrt{r}\left(\frac{\mathit{\partial }{h}_3^{\mathit{sc}}}{\mathit{\partial }r}-i{\mathit{\kappa }}_0{h}_3^{\mathit{sc}}\right)=0,\\ \hfill \end{array}\end{array}$$(7) ) have the asymptotic behavior(13) $$\begin{array}{c}\hfill e_3^{\mathit{sc}}(\mathit{x})=\frac{e^{i{\mathit{\kappa }}_{0}r}}{\sqrt{r}}{e}^{\infty }(\widehat{\mathit{x}})+\mathcal{O}(r^{-3/2}),h_3^{\mathit{sc}}(\mathit{x})=\frac{e^{i{\mathit{\kappa }}_{0}r}}{\sqrt{r}}{h}^{\infty }(\widehat{\mathit{x}})+\mathcal{O}(r^{-3/2}),\end{array}$$(13)

where $\widehat{\mathit{x}}=\mathit{x}/|\mathit{x}|.$ The pair $(e^{\infty },h^{\infty })$ is called the far-field pattern corresponding to the scattering problem (4(4) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{\Delta }{e}_3^{\mathit{int}}+{\mathit{\kappa }}_1^2{e}_3^{\mathit{int}}=0,\mathrm{\Delta }{h}_3^{\mathit{int}}+{\mathit{\kappa }}_1^2{h}_3^{\mathit{int}}=0,\mathit{x}& \in {\mathrm{\Omega }}_1,\hfill \\ \hfill \mathrm{\Delta }{e}_3^{\mathit{ext}}+{\mathit{\kappa }}_0^2{e}_3^{\mathit{ext}}=0,\mathrm{\Delta }{h}_3^{\mathit{ext}}+{\mathit{\kappa }}_0^2{h}_3^{\mathit{ext}}=0,\mathit{x}& \in {\mathrm{\Omega }}_0,\hfill \end{array}\end{array}$$(4) )–(7(7) $$\begin{array}{c}\hfill \begin{array}{c}\hfill \underset{r\to \infty }{lim}\sqrt{r}\left(\frac{\mathit{\partial }{e}_3^{\mathit{sc}}}{\mathit{\partial }r}-i{\mathit{\kappa }}_0{e}_3^{\mathit{sc}}\right)=0,\underset{r\to \infty }{lim}\sqrt{r}\left(\frac{\mathit{\partial }{h}_3^{\mathit{sc}}}{\mathit{\partial }r}-i{\mathit{\kappa }}_0{h}_3^{\mathit{sc}}\right)=0,\\ \hfill \end{array}\end{array}$$(7) ). Its knowledge is essential for the inverse problem and using (11(11) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill e_3^{\mathit{int}}(\mathit{x})& =-({\mathcal{D}}_1{\mathit{\varphi }}_1)(\mathit{x})+({\mathcal{S}}_1{\mathit{\eta }}_1)(\mathit{x}),\hfill & \hfill \mathit{x}\in {\mathrm{\Omega }}_1,\\ \hfill h_3^{\mathit{int}}(\mathit{x})& =-({\mathcal{D}}_1{\mathit{\psi }}_1)(\mathit{x})+({\mathcal{S}}_1{\mathit{\xi }}_1)(\mathit{x}),\hfill & \hfill \mathit{x}\in {\mathrm{\Omega }}_1,\\ \hfill e_3^{\mathit{ext}}(\mathit{x})& =({\mathcal{D}}_0{\mathit{\varphi }}_0)(\mathit{x})-({\mathcal{S}}_0{\mathit{\eta }}_0)(\mathit{x}),\hfill & \hfill \mathit{x}\in {\mathrm{\Omega }}_0,\\ \hfill h_3^{\mathit{ext}}(\mathit{x})& =({\mathcal{D}}_0{\mathit{\psi }}_0)(\mathit{x})-({\mathcal{S}}_0{\mathit{\xi }}_0)(\mathit{x}),\hfill & \hfill \mathit{x}\in {\mathrm{\Omega }}_0,\end{array}\end{array}$$(11) ) we can compute it by: (14) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill e^{\infty }(\widehat{\mathit{x}})& =(D^{\infty }{\mathit{\varphi }}_0)(\widehat{\mathit{x}})-(S^{\infty }{\mathit{\eta }}_0)(\widehat{\mathit{x}}),\hfill & \hfill \widehat{\mathit{x}}\in S,\\ \hfill h^{\infty }(\widehat{\mathit{x}})& =(D^{\infty }{\mathit{\psi }}_0)(\widehat{\mathit{x}})-(S^{\infty }{\mathit{\xi }}_0)(\widehat{\mathit{x}}),\hfill & \hfill \widehat{\mathit{x}}\in S,\\ \hfill \end{array}\end{array}$$(14)

where $S$ is the unit ball. The far-field operators are given by: (15) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill (S^{\infty }f)(\widehat{\mathit{x}})& ={\int }_{\mathrm{\Gamma }}{\mathrm{\Phi }}^{\infty }(\widehat{\mathit{x}},\mathit{y})f(\mathit{y})\mathrm{d}s(\mathit{y}),\hfill & \hfill \widehat{\mathit{x}}\in S,\\ \hfill (D^{\infty }f)(\widehat{\mathit{x}})& ={\int }_{\mathrm{\Gamma }}\frac{\mathit{\partial }{\mathrm{\Phi }}^{\infty }}{\mathit{\partial }n(\mathit{y})}(\widehat{\mathit{x}},\mathit{y})f(\mathit{y})\mathrm{d}s(\mathit{y}),\hfill & \hfill \widehat{\mathit{x}}\in S,\end{array}\end{array}$$(15)

where ${\mathrm{\Phi }}^{\infty }$ is the far-field of the Green function $\mathrm{\Phi },$ given by:$${\mathrm{\Phi }}^{\infty }(\widehat{\mathit{x}},\mathit{y})=\frac{e^{i\mathit{\pi }/4}}{\sqrt{8\mathit{\pi }{\mathit{\kappa }}_0}}{e}^{-i{\mathit{\kappa }}_0\widehat{\mathit{x}}·\mathit{y}}.$$

3. The inverse problem

The inverse scattering problem, we address here, reads: find the shape and the position of the inclusion $\mathrm{\Omega },$ meaning reconstruct its boundary $\mathrm{\Gamma }$, given the far-field patterns $(e^{\infty }(\widehat{\mathit{x}}),h^{\infty }(\widehat{\mathit{x}})),$ for all $\widehat{\mathit{x}}\in S,$ for one or few incident fields (6(6) $$\begin{array}{c}\hfill \begin{array}{c}\hfill e_3^{\mathit{inc}}(\mathit{x})=\frac{1}{\sqrt{{\mathit{ϵ}}_0}}sin\mathit{\theta }{e}^{i{\mathit{\kappa }}_0(xcos\mathit{\varphi }+ysin\mathit{\varphi })},h_3^{\mathit{inc}}(\mathit{x})=0.\end{array}\end{array}$$(6) ).

3.1. The integral equation method

To solve the inverse problem we apply the method of non-linear boundary integral equations, which in our case, results to a system of four integral equations on the unknown boundary and one on the unit circle where the far-field data are defined. This method was first introduced in [23] and further considered in various inverse problems, see for instance, [25,27,32,33]. Since the direct problem was solved with the direct method (Green’s formulas), in order to obtain our numerical data, here we adopt a different approach based on the indirect integral equation method, using simple representations for the fields.

We assume a double-layer representation for the interior fields and a single-layer representation for the exterior fields. Thus, we set(16) $$\begin{array}{c}\hfill \begin{array}{ccccc}\hfill e_3^{\mathit{int}}(\mathit{x})& =\frac{1}{{\widetilde{\mathit{ϵ}}}_1}({\mathcal{D}}_1{\mathit{\varphi }}_e)(\mathit{x}),\hfill & \hfill h_3^{\mathit{int}}(\mathit{x})& =\frac{1}{{\tilde{\mathit{\mu }}}_1}({\mathcal{D}}_1{\mathit{\varphi }}_h)(\mathit{x}),\hfill & \mathit{x}\in {\mathrm{\Omega }}_1,\\ \hfill e_3^{\mathit{sc}}(\mathit{x})& =\frac{1}{{\widetilde{\mathit{ϵ}}}_0}({\mathcal{S}}_0{\mathit{\psi }}_e)(\mathit{x}),\hfill & \hfill h_3^{\mathit{sc}}(\mathit{x})& =\frac{1}{{\tilde{\mathit{\mu }}}_0}({\mathcal{S}}_0{\mathit{\psi }}_h)(\mathit{x}),\hfill & \mathit{x}\in {\mathrm{\Omega }}_0.\end{array}\end{array}$$(16)

Substituting the above representations in the transmission conditions (5(5) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill e_3^{\mathit{int}}& =e_3^{\mathit{ext}},\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\\ \hfill {\tilde{\mathit{\mu }}}_1\mathit{\omega }\frac{\mathit{\partial }{h}_3^{\mathit{int}}}{\mathit{\partial }n}+{\mathit{\beta }}_1\frac{\mathit{\partial }{e}_3^{\mathit{int}}}{\mathit{\partial }\mathit{\tau }}& ={\tilde{\mathit{\mu }}}_0\mathit{\omega }\frac{\mathit{\partial }{h}_3^{\mathit{ext}}}{\mathit{\partial }n}+{\mathit{\beta }}_0\frac{\mathit{\partial }{e}_3^{\mathit{ext}}}{\mathit{\partial }\mathit{\tau }},\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\\ \hfill h_3^{\mathit{int}}& =h_3^{\mathit{ext}},\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\\ \hfill {\widetilde{\mathit{ϵ}}}_1\mathit{\omega }\frac{\mathit{\partial }{e}_3^{\mathit{int}}}{\mathit{\partial }n}-{\mathit{\beta }}_1\frac{\mathit{\partial }{h}_3^{\mathit{int}}}{\mathit{\partial }\mathit{\tau }}& ={\widetilde{\mathit{ϵ}}}_0\mathit{\omega }\frac{\mathit{\partial }{e}_3^{\mathit{ext}}}{\mathit{\partial }n}-{\mathit{\beta }}_0\frac{\mathit{\partial }{h}_3^{\mathit{ext}}}{\mathit{\partial }\mathit{\tau }},\hfill & \hfill \mathit{x}\in \mathrm{\Gamma },\end{array}\end{array}$$(5) ) and considering the well-known jump relations, we get the system of integral equations on $\mathrm{\Gamma }$ (17) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{1}{{\widetilde{\mathit{ϵ}}}_1}\left(D_1-\frac{1}{2}\right){\mathit{\varphi }}_e-\frac{1}{{\widetilde{\mathit{ϵ}}}_0}{S}_0{\mathit{\psi }}_e& =e_3^{\mathit{inc}},\hfill \\ \hfill \mathit{\omega }N{D}_1{\mathit{\varphi }}_h+\frac{{\mathit{\beta }}_1}{{\widetilde{\mathit{ϵ}}}_1}\left(T{D}_1-\frac{1}{2}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\tau }}\right){\mathit{\varphi }}_e-\mathit{\omega }\left(N{S}_0-\frac{1}{2}\right){\mathit{\psi }}_h-\frac{{\mathit{\beta }}_0}{{\widetilde{\mathit{ϵ}}}_0}T{S}_0{\mathit{\psi }}_e& ={\mathit{\beta }}_0\frac{\mathit{\partial }{e}_3^{\mathit{inc}}}{\mathit{\partial }\mathit{\tau }},\hfill \\ \hfill \frac{1}{{\tilde{\mathit{\mu }}}_1}\left(D_1-\frac{1}{2}\right){\mathit{\varphi }}_h-\frac{1}{{\tilde{\mathit{\mu }}}_0}{S}_0{\mathit{\psi }}_h& =0,\hfill \\ \hfill \mathit{\omega }N{D}_1{\mathit{\varphi }}_e-\frac{{\mathit{\beta }}_1}{{\tilde{\mathit{\mu }}}_1}\left(T{D}_1-\frac{1}{2}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\tau }}\right){\mathit{\varphi }}_h-\mathit{\omega }\left(N{S}_0-\frac{1}{2}\right){\mathit{\psi }}_e+\frac{{\mathit{\beta }}_0}{{\tilde{\mathit{\mu }}}_0}T{S}_0{\mathit{\psi }}_h& ={\widetilde{\mathit{ϵ}}}_0\mathit{\omega }\frac{\mathit{\partial }{e}_3^{\mathit{inc}}}{\mathit{\partial }n}.\hfill \end{array}\end{array}$$(17)

In addition, given the far-field operators (15(15) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill (S^{\infty }f)(\widehat{\mathit{x}})& ={\int }_{\mathrm{\Gamma }}{\mathrm{\Phi }}^{\infty }(\widehat{\mathit{x}},\mathit{y})f(\mathit{y})\mathrm{d}s(\mathit{y}),\hfill & \hfill \widehat{\mathit{x}}\in S,\\ \hfill (D^{\infty }f)(\widehat{\mathit{x}})& ={\int }_{\mathrm{\Gamma }}\frac{\mathit{\partial }{\mathrm{\Phi }}^{\infty }}{\mathit{\partial }n(\mathit{y})}(\widehat{\mathit{x}},\mathit{y})f(\mathit{y})\mathrm{d}s(\mathit{y}),\hfill & \hfill \widehat{\mathit{x}}\in S,\end{array}\end{array}$$(15) ) and the representations (16(16) $$\begin{array}{c}\hfill \begin{array}{ccccc}\hfill e_3^{\mathit{int}}(\mathit{x})& =\frac{1}{{\widetilde{\mathit{ϵ}}}_1}({\mathcal{D}}_1{\mathit{\varphi }}_e)(\mathit{x}),\hfill & \hfill h_3^{\mathit{int}}(\mathit{x})& =\frac{1}{{\tilde{\mathit{\mu }}}_1}({\mathcal{D}}_1{\mathit{\varphi }}_h)(\mathit{x}),\hfill & \mathit{x}\in {\mathrm{\Omega }}_1,\\ \hfill e_3^{\mathit{sc}}(\mathit{x})& =\frac{1}{{\widetilde{\mathit{ϵ}}}_0}({\mathcal{S}}_0{\mathit{\psi }}_e)(\mathit{x}),\hfill & \hfill h_3^{\mathit{sc}}(\mathit{x})& =\frac{1}{{\tilde{\mathit{\mu }}}_0}({\mathcal{S}}_0{\mathit{\psi }}_h)(\mathit{x}),\hfill & \mathit{x}\in {\mathrm{\Omega }}_0.\end{array}\end{array}$$(16) ) of the exterior fields, we see that the unknown boundary $\mathrm{\Gamma }$ and the densities ${\mathit{\psi }}_e$ and ${\mathit{\psi }}_h$ satisfy also the far-field equations (18a) $$\begin{array}{cc}\hfill \frac{1}{{\widetilde{\mathit{ϵ}}}_0}{S}^{\infty }{\mathit{\psi }}_e& =e^{\infty },\text{on}S,\hfill \end{array}$$(18a) (18b) $$\begin{array}{cc}\hfill \frac{1}{{\tilde{\mathit{\mu }}}_0}{S}^{\infty }{\mathit{\psi }}_h& =h^{\infty },\text{on}S,\hfill \end{array}$$(18b) where the right-hand sides are the known far-field patterns from the direct problem. The Equation (17(17) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{1}{{\widetilde{\mathit{ϵ}}}_1}\left(D_1-\frac{1}{2}\right){\mathit{\varphi }}_e-\frac{1}{{\widetilde{\mathit{ϵ}}}_0}{S}_0{\mathit{\psi }}_e& =e_3^{\mathit{inc}},\hfill \\ \hfill \mathit{\omega }N{D}_1{\mathit{\varphi }}_h+\frac{{\mathit{\beta }}_1}{{\widetilde{\mathit{ϵ}}}_1}\left(T{D}_1-\frac{1}{2}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\tau }}\right){\mathit{\varphi }}_e-\mathit{\omega }\left(N{S}_0-\frac{1}{2}\right){\mathit{\psi }}_h-\frac{{\mathit{\beta }}_0}{{\widetilde{\mathit{ϵ}}}_0}T{S}_0{\mathit{\psi }}_e& ={\mathit{\beta }}_0\frac{\mathit{\partial }{e}_3^{\mathit{inc}}}{\mathit{\partial }\mathit{\tau }},\hfill \\ \hfill \frac{1}{{\tilde{\mathit{\mu }}}_1}\left(D_1-\frac{1}{2}\right){\mathit{\varphi }}_h-\frac{1}{{\tilde{\mathit{\mu }}}_0}{S}_0{\mathit{\psi }}_h& =0,\hfill \\ \hfill \mathit{\omega }N{D}_1{\mathit{\varphi }}_e-\frac{{\mathit{\beta }}_1}{{\tilde{\mathit{\mu }}}_1}\left(T{D}_1-\frac{1}{2}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\tau }}\right){\mathit{\varphi }}_h-\mathit{\omega }\left(N{S}_0-\frac{1}{2}\right){\mathit{\psi }}_e+\frac{{\mathit{\beta }}_0}{{\tilde{\mathit{\mu }}}_0}T{S}_0{\mathit{\psi }}_h& ={\widetilde{\mathit{ϵ}}}_0\mathit{\omega }\frac{\mathit{\partial }{e}_3^{\mathit{inc}}}{\mathit{\partial }n}.\hfill \end{array}\end{array}$$(17) ) in matrix form reads(19) $$\begin{array}{c}\hfill (\mathbf{T}+\mathbf{K})\mathit{\varphi }=\mathbf{b},\end{array}$$(19)

where$$\begin{array}{cccc}\hfill \mathbf{T}& =\left(\begin{array}{cccc}{\displaystyle \frac{\mathit{\omega }}{2}}& {\displaystyle \frac{{\mathit{\beta }}_1}{2{\tilde{\mathit{\mu }}}_1}}{\mathit{\partial }}_{\mathit{\tau }}& 0& 0\\ [10pt]0& -{\displaystyle \frac{1}{2{\tilde{\mathit{\mu }}}_1}}& 0& 0\\ 0& 0& {\displaystyle \frac{\mathit{\omega }}{2}}& -{\displaystyle \frac{{\mathit{\beta }}_1}{2{\widetilde{\mathit{ϵ}}}_1}}{\mathit{\partial }}_{\mathit{\tau }}\\ [10pt]0& 0& 0& -{\displaystyle \frac{1}{2{\widetilde{\mathit{ϵ}}}_1}}\end{array}\right),\hfill & \hfill \mathbf{K}& =\left(\begin{array}{cccc}-\mathit{\omega }N{S}_0& -{\displaystyle \frac{{\mathit{\beta }}_1}{{\tilde{\mathit{\mu }}}_1}}T{D}_1& {\displaystyle \frac{{\mathit{\beta }}_0}{{\tilde{\mathit{\mu }}}_0}}T{S}_0& \mathit{\omega }N{D}_1\\ [10pt]0& {\displaystyle \frac{1}{{\tilde{\mathit{\mu }}}_1}}{D}_1& -{\displaystyle \frac{1}{{\tilde{\mathit{\mu }}}_0}}{S}_0& 0\\ -{\displaystyle \frac{{\mathit{\beta }}_0}{{\widetilde{\mathit{ϵ}}}_0}}T{S}_0& \mathit{\omega }N{D}_1& -\mathit{\omega }N{S}_0& {\displaystyle \frac{{\mathit{\beta }}_1}{{\widetilde{\mathit{ϵ}}}_1}}T{D}_1\\ [10pt]-{\displaystyle \frac{1}{{\widetilde{\mathit{ϵ}}}_0}}{S}_0& 0& 0& {\displaystyle \frac{1}{{\widetilde{\mathit{ϵ}}}_1}}{D}_1\end{array}\right),\hfill \\ \hfill \mathit{\varphi }& =\left(\begin{array}{c}{\mathit{\psi }}_e\\ {\mathit{\varphi }}_h\\ {\mathit{\psi }}_h\\ {\mathit{\varphi }}_e\end{array}\right),\hfill & \hfill \mathbf{b}& =\left(\begin{array}{c}{\widetilde{\mathit{ϵ}}}_0\mathit{\omega }{\mathit{\partial }}_n\\ 0\\ {\mathit{\beta }}_0{\mathit{\partial }}_{\mathit{\tau }}\\ 1\end{array}\right)e_3^{\mathit{inc}}.\hfill \end{array}$$

The matrix $\mathbf{T}$ due to its special form and the boundness of ${\mathit{\partial }}_{\mathit{\tau }}:H^{1/2}(\mathrm{\Gamma })\to H^{-1/2}(\mathrm{\Gamma })$ has a bounded inverse given by:(20) $$\begin{array}{c}\hfill {\mathbf{T}}^{-1}=\left(\begin{array}{cccc}{\displaystyle \frac{2}{\mathit{\omega }}}& {\displaystyle \frac{2{\mathit{\beta }}_1}{\mathit{\omega }}}{\mathit{\partial }}_{\mathit{\tau }}& 0& 0\\ [10pt]0& -2{\tilde{\mathit{\mu }}}_1& 0& 0\\ [6pt]0& 0& {\displaystyle \frac{2}{\mathit{\omega }}}& -{\displaystyle \frac{2{\mathit{\beta }}_1}{\mathit{\omega }}}{\mathit{\partial }}_{\mathit{\tau }}\\ [10pt]0& 0& 0& -2{\widetilde{\mathit{ϵ}}}_1\end{array}\right).\end{array}$$(20)

Then, Equation (19(19) $$\begin{array}{c}\hfill (\mathbf{T}+\mathbf{K})\mathit{\varphi }=\mathbf{b},\end{array}$$(19) ) takes the form(21) $$\begin{array}{c}\hfill (\mathbf{I}+\mathbf{C})\mathit{\varphi }=\mathbf{g},\end{array}$$(21)

where now $\mathbf{I}$ is the identity matrix and$$\begin{array}{cc}\hfill \mathbf{C}& ={\mathbf{T}}^{-1}\mathbf{K}=\left(\begin{array}{cccc}-2N{S}_0& 0& {\displaystyle \frac{2}{\mathit{\omega }{\tilde{\mathit{\mu }}}_0}}({\mathit{\beta }}_0-{\mathit{\beta }}_1)T{S}_0& 2N{D}_1\\ 0& -2D_1& 2{\displaystyle \frac{{\tilde{\mathit{\mu }}}_1}{{\tilde{\mathit{\mu }}}_0}}{S}_0& 0\\ -{\displaystyle \frac{2}{\mathit{\omega }{\widetilde{\mathit{ϵ}}}_0}}({\mathit{\beta }}_0-{\mathit{\beta }}_1)T{S}_0& 2N{D}_1& -2N{S}_0& 0\\ 2{\displaystyle \frac{{\widetilde{\mathit{ϵ}}}_1}{{\widetilde{\mathit{ϵ}}}_0}}{S}_0& 0& 0& -2D_1\end{array}\right),\hfill \\ \hfill \mathbf{g}& ={\mathbf{T}}^{-1}\mathbf{b}=\left(\begin{array}{c}2{\widetilde{\mathit{ϵ}}}_0{\mathit{\partial }}_n\\ 0\\ {\displaystyle \frac{2}{\mathit{\omega }}}({\mathit{\beta }}_0-{\mathit{\beta }}_1){\mathit{\partial }}_{\mathit{\tau }}\\ -2{\widetilde{\mathit{ϵ}}}_1\end{array}\right)e_3^{\mathit{inc}}.\hfill \end{array}$$

Using the mapping properties of the integral operators [34], we see that the operator $\mathbf{C}:{(H^{-1/2}(\mathrm{\Gamma })\times H^{1/2}(\mathrm{\Gamma }))}^2\to {(H^{-3/2}(\mathrm{\Gamma })\times H^{-1/2}(\mathrm{\Gamma }))}^2$ is compact.

We observe that we have six equations (21(21) $$\begin{array}{c}\hfill (\mathbf{I}+\mathbf{C})\mathit{\varphi }=\mathbf{g},\end{array}$$(21) ) and () for the five unknowns: $\mathrm{\Gamma }$ and the four densities. Thus, we consider the linear combination ${\widetilde{\mathit{ϵ}}}_0·$(18a(18a) $$\begin{array}{cc}\hfill \frac{1}{{\widetilde{\mathit{ϵ}}}_0}{S}^{\infty }{\mathit{\psi }}_e& =e^{\infty },\text{on}S,\hfill \end{array}$$(18a) ) + ${\tilde{\mathit{\mu }}}_0·$(18b(18b) $$\begin{array}{cc}\hfill \frac{1}{{\tilde{\mathit{\mu }}}_0}{S}^{\infty }{\mathit{\psi }}_h& =h^{\infty },\text{on}S,\hfill \end{array}$$(18b) ) as a replacement for the far-field equations in order to state the following theorem as a formulation of the inverse problem.

Theorem 3.1:

Given the incident field (6(6) $$\begin{array}{c}\hfill \begin{array}{c}\hfill e_3^{\mathit{inc}}(\mathit{x})=\frac{1}{\sqrt{{\mathit{ϵ}}_0}}sin\mathit{\theta }{e}^{i{\mathit{\kappa }}_0(xcos\mathit{\varphi }+ysin\mathit{\varphi })},h_3^{\mathit{inc}}(\mathit{x})=0.\end{array}\end{array}$$(6) ) and the far-field patterns $(e^{\infty }(\widehat{\mathit{x}}),h^{\infty }(\widehat{\mathit{x}})),$ for all $\widehat{\mathit{x}}\in S,$ if the boundary $\mathrm{\Gamma }$ and the densities ${\mathit{\psi }}_e,{\mathit{\varphi }}_h,{\mathit{\psi }}_h$ and ${\mathit{\varphi }}_e$ satisfy the system of equations (22a) $$\begin{array}{cc}\hfill {\mathit{\psi }}_e-2N{S}_0{\mathit{\psi }}_e+{\displaystyle \frac{2}{\mathit{\omega }{\tilde{\mathit{\mu }}}_0}}({\mathit{\beta }}_0-{\mathit{\beta }}_1)T{S}_0{\mathit{\psi }}_h+2N{D}_1{\mathit{\varphi }}_e& =2{\widetilde{\mathit{ϵ}}}_0{\mathit{\partial }}_n{e}_3^{\mathit{inc}},\hfill \end{array}$$(22a) (22b) $$\begin{array}{cc}\hfill {\mathit{\varphi }}_h-2D_1{\mathit{\varphi }}_h+2{\displaystyle \frac{{\tilde{\mathit{\mu }}}_1}{{\tilde{\mathit{\mu }}}_0}}{S}_0{\mathit{\psi }}_h& =0,\hfill \end{array}$$(22b) (22c) $$\begin{array}{cc}\hfill -{\displaystyle \frac{2}{\mathit{\omega }{\widetilde{\mathit{ϵ}}}_0}}({\mathit{\beta }}_0-{\mathit{\beta }}_1)T{S}_0{\mathit{\psi }}_e+2N{D}_1{\mathit{\varphi }}_h+{\mathit{\psi }}_h-2N{S}_0{\mathit{\psi }}_h& ={\displaystyle \frac{2}{\mathit{\omega }}}({\mathit{\beta }}_0-{\mathit{\beta }}_1){\mathit{\partial }}_{\mathit{\tau }}{e}_3^{\mathit{inc}},\hfill \end{array}$$(22c) (22d) $$\begin{array}{cc}\hfill 2{\displaystyle \frac{{\widetilde{\mathit{ϵ}}}_1}{{\widetilde{\mathit{ϵ}}}_0}}{S}_0{\mathit{\psi }}_e+{\mathit{\varphi }}_e-2D_1{\mathit{\varphi }}_e& =-2{\widetilde{\mathit{ϵ}}}_1{e}_3^{\mathit{inc}},\hfill \end{array}$$(22d) (22e) $$\begin{array}{cc}\hfill S^{\infty }{\mathit{\psi }}_e+S^{\infty }{\mathit{\psi }}_h& ={\widetilde{\mathit{ϵ}}}_0{e}^{\infty }+{\tilde{\mathit{\mu }}}_0{h}^{\infty },\hfill \end{array}$$(22e) then, $\mathrm{\Gamma }$ solves the inverse problem.

The integral operators in () are linear with respect to the densities but non-linear with respect to the unknown boundary $\mathrm{\Gamma }.$ The smoothness of the kernels in the far-field Equation (22e(22e) $$\begin{array}{cc}\hfill S^{\infty }{\mathit{\psi }}_e+S^{\infty }{\mathit{\psi }}_h& ={\widetilde{\mathit{ϵ}}}_0{e}^{\infty }+{\tilde{\mathit{\mu }}}_0{h}^{\infty },\hfill \end{array}$$(22e) ) reflects the ill-posedness of the inverse problem.

To solve the above system of equations, we consider the method first introduced in [29] and then applied in different problems, see for instance [26,30,35]. More precisely, given an initial approximation for the boundary $\mathrm{\Gamma }$, we solve the subsystem (22a(22a) $$\begin{array}{cc}\hfill {\mathit{\psi }}_e-2N{S}_0{\mathit{\psi }}_e+{\displaystyle \frac{2}{\mathit{\omega }{\tilde{\mathit{\mu }}}_0}}({\mathit{\beta }}_0-{\mathit{\beta }}_1)T{S}_0{\mathit{\psi }}_h+2N{D}_1{\mathit{\varphi }}_e& =2{\widetilde{\mathit{ϵ}}}_0{\mathit{\partial }}_n{e}_3^{\mathit{inc}},\hfill \end{array}$$(22a) )–(22d(22d) $$\begin{array}{cc}\hfill 2{\displaystyle \frac{{\widetilde{\mathit{ϵ}}}_1}{{\widetilde{\mathit{ϵ}}}_0}}{S}_0{\mathit{\psi }}_e+{\mathit{\varphi }}_e-2D_1{\mathit{\varphi }}_e& =-2{\widetilde{\mathit{ϵ}}}_1{e}_3^{\mathit{inc}},\hfill \end{array}$$(22d) ) for the densities ${\mathit{\psi }}_e,{\mathit{\varphi }}_h,{\mathit{\psi }}_h$ and ${\mathit{\varphi }}_e.$ Then, keeping the densities ${\mathit{\psi }}_e$ and ${\mathit{\psi }}_h$ fixed we linearize the far-field Equation (22e(22e) $$\begin{array}{cc}\hfill S^{\infty }{\mathit{\psi }}_e+S^{\infty }{\mathit{\psi }}_h& ={\widetilde{\mathit{ϵ}}}_0{e}^{\infty }+{\tilde{\mathit{\mu }}}_0{h}^{\infty },\hfill \end{array}$$(22e) ) with respect to the boundary. The linearized equation is solved to obtain the update for the boundary. The linearization is performed using Fréchet derivatives of the operators and we also regularize the ill-posed last equation.

To present the proposed method in detail, we consider the following parametrization for the boundary$$\mathrm{\Gamma }=\{\mathit{z}(t)=r(t)(cost,sint):t\in [0,2\mathit{\pi }]\},$$

where $\mathit{z}:R\to R^2$ is a $C^2$-smooth, $2\mathit{\pi }$-periodic, injective in $[0,2\mathit{\pi }),$ meaning that ${\mathit{z}}^{\prime }(t)\ne 0,$ for all $t\in [0,2\mathit{\pi }].$ The non-negative function r represents the radial distance of $\mathrm{\Gamma }$ from the origin. Then, we define$$\begin{array}{cc}\hfill {\mathit{\zeta }}_e(t)& ={\mathit{\psi }}_e(\mathit{z}(t)),{\mathit{\zeta }}_h(t)={\mathit{\psi }}_h(\mathit{z}(t)),t\in [0,2\mathit{\pi }]\hfill \\ \hfill {\mathit{\xi }}_e(t)& ={\mathit{\varphi }}_e(\mathit{z}(t)),{\mathit{\xi }}_h(t)={\mathit{\varphi }}_h(\mathit{z}(t)),t\in [0,2\mathit{\pi }]\hfill \end{array}$$

and the parametrized form of () is given by:(23) $$\begin{array}{c}\hfill \left(\begin{array}{c}{\mathcal{A}}_1\\ {\mathcal{A}}_2\\ {\mathcal{A}}_3\\ {\mathcal{A}}_4\\ {\mathcal{A}}_5\end{array}\right)(r;{\mathit{\zeta }}_e)+\left(\begin{array}{c}{\mathcal{B}}_1\\ {\mathcal{B}}_2\\ {\mathcal{B}}_3\\ {\mathcal{B}}_4\\ {\mathcal{B}}_5\end{array}\right)(r;{\mathit{\xi }}_h)+\left(\begin{array}{c}{\mathcal{C}}_1\\ {\mathcal{C}}_2\\ {\mathcal{C}}_3\\ {\mathcal{C}}_4\\ {\mathcal{C}}_5\end{array}\right)(r;{\mathit{\zeta }}_h)+\left(\begin{array}{c}{\mathcal{D}}_1\\ {\mathcal{D}}_2\\ {\mathcal{D}}_3\\ {\mathcal{D}}_4\\ {\mathcal{D}}_5\end{array}\right)(r;{\mathit{\xi }}_e)=\left(\begin{array}{c}{\mathcal{F}}_1\\ {\mathcal{F}}_2\\ {\mathcal{F}}_3\\ {\mathcal{F}}_4\\ {\mathcal{F}}_5\end{array}\right),\end{array}$$(23)

with the parametrized operators$$\begin{array}{cc}\hfill ({\mathcal{A}}_1(r;\mathit{\zeta }))(t)& =({\mathcal{C}}_3(r;\mathit{\zeta }))(t)=\mathit{\zeta }(t)-2{\int }_0^{2\mathit{\pi }}{M}^{N{S}_0}(t,s)\mathit{\zeta }(s)\mathrm{d}s,\hfill \\ \hfill ({\mathcal{A}}_3(r;\mathit{\zeta }))(t)& =-\frac{{\tilde{\mathit{\mu }}}_0}{{\widetilde{\mathit{ϵ}}}_0}({\mathcal{C}}_1(r;\mathit{\zeta }))(t)=-\frac{2}{\mathit{\omega }{\widetilde{\mathit{ϵ}}}_0}({\mathit{\beta }}_0-{\mathit{\beta }}_1){\int }_0^{2\mathit{\pi }}{M}^{T{S}_0}(t,s)\mathit{\zeta }(s)\mathrm{d}s,\hfill \\ \hfill ({\mathcal{A}}_4(r;\mathit{\zeta }))(t)& =\frac{{\tilde{\mathit{\mu }}}_0{\widetilde{\mathit{ϵ}}}_1}{{\tilde{\mathit{\mu }}}_1{\widetilde{\mathit{ϵ}}}_0}({\mathcal{C}}_2(r;\mathit{\zeta }))(t)=2\frac{{\widetilde{\mathit{ϵ}}}_1}{{\widetilde{\mathit{ϵ}}}_0}{\int }_0^{2\mathit{\pi }}{M}^{S_0}(t,s)\mathit{\zeta }(s)\mathrm{d}s,\hfill \\ \hfill ({\mathcal{A}}_5(r;\mathit{\zeta }))(t)& =({\mathcal{C}}_5(r;\mathit{\zeta }))(t)={\int }_0^{2\mathit{\pi }}{\mathrm{\Phi }}^{\infty }(\widehat{\mathit{z}}(t),\mathit{z}(s))\mathit{\zeta }(s)|{\mathit{z}}^{\prime }(s)|\mathrm{d}s,\hfill \\ \hfill ({\mathcal{B}}_2(r;\mathit{\xi }))(t)& =({\mathcal{D}}_4(r;\mathit{\xi }))(t)=\mathit{\xi }(t)-2{\int }_0^{2\mathit{\pi }}{M}^{D_1}(t,s)\mathit{\xi }(s)\mathrm{d}s,\hfill \\ \hfill ({\mathcal{B}}_3(r;\mathit{\xi }))(t)& =({\mathcal{D}}_1(r;\mathit{\xi }))(t)=2{\int }_0^{2\mathit{\pi }}{M}^{N{D}_1}(t,s)\mathit{\xi }(s)\mathrm{d}s,\hfill \\ \hfill \end{array}$$

and the right-hand side$$\begin{array}{cccc}\hfill ({\mathcal{F}}_1(r))(t)& =2{\widetilde{\mathit{ϵ}}}_0{\mathit{\partial }}_n{e}_3^{\mathit{inc}}(\mathit{z}(t)),\hfill & \hfill ({\mathcal{F}}_3(r))(t)& ={\displaystyle \frac{2}{\mathit{\omega }}}({\mathit{\beta }}_0-{\mathit{\beta }}_1){\mathit{\partial }}_{\mathit{\tau }}{e}_3^{\mathit{inc}}(\mathit{z}(t)),\hfill \\ \hfill ({\mathcal{F}}_4(r))(t)& =-2{\widetilde{\mathit{ϵ}}}_1{e}_3^{\mathit{inc}}(\mathit{z}(t)),\hfill & \hfill ({\mathcal{F}}_5)(t)& ={\widetilde{\mathit{ϵ}}}_0{e}^{\infty }(\widehat{\mathit{z}}(t))+{\tilde{\mathit{\mu }}}_0{h}^{\infty }(\widehat{\mathit{z}}(t)).\hfill \end{array}$$

In addition, we set ${\mathcal{A}}_2={\mathcal{B}}_1={\mathcal{B}}_4={\mathcal{B}}_5={\mathcal{C}}_4={\mathcal{D}}_2={\mathcal{D}}_3={\mathcal{D}}_5={\mathcal{F}}_2=0.$ The matrix $M^{K_j}$ denotes the discretized kernel of the operator $K_j.$ The explicit forms of the kernels can be found for example, in [8, Equation 4.3]. The operators ${\mathcal{A}}_k,{\mathcal{B}}_k,{\mathcal{C}}_k,{\mathcal{D}}_k,$ $k=1,2,3,4,5$ act on the densities and the first variable r shows the dependence on the unknown parametrization of the boundary. Only ${\mathcal{F}}_5$ is independent of the radial function.

Let the function q stand for the radial function of the perturbed boundary$${\mathrm{\Gamma }}_q=\{\mathit{q}(t)=q(t)(cost,sint):t\in [0,2\mathit{\pi }]\}.$$

Then the iterative method reads:

Iterative Scheme 1:

Let $r^{(0)}$ be an initial approximation of the radial function. Then, in the kth iteration step:

(i)

We assume that we know $r^{(k-1)}$ and we solve the subsystem (24) $$\begin{array}{cc}& \left(\begin{array}{c}{\mathcal{A}}_1\\ {\mathcal{A}}_2\\ {\mathcal{A}}_3\\ {\mathcal{A}}_4\end{array}\right)(r^{(k-1)};{\mathit{\zeta }}_e)+\left(\begin{array}{c}{\mathcal{B}}_1\\ {\mathcal{B}}_2\\ {\mathcal{B}}_3\\ {\mathcal{B}}_4\end{array}\right)(r^{(k-1)};{\mathit{\xi }}_h)+\left(\begin{array}{c}{\mathcal{C}}_1\\ {\mathcal{C}}_2\\ {\mathcal{C}}_3\\ {\mathcal{C}}_4\end{array}\right)(r^{(k-1)};{\mathit{\zeta }}_h)\hfill \\ \hfill & +\left(\begin{array}{c}{\mathcal{D}}_1\\ {\mathcal{D}}_2\\ {\mathcal{D}}_3\\ {\mathcal{D}}_4\end{array}\right)(r^{(k-1)};{\mathit{\xi }}_e)=\left(\begin{array}{c}{\mathcal{F}}_1\\ {\mathcal{F}}_2\\ {\mathcal{F}}_3\\ {\mathcal{F}}_4\end{array}\right),\hfill \end{array}$$(24) to obtain the densities ${\mathit{\zeta }}_e^{(k)},{\mathit{\xi }}_h^{(k)},{\mathit{\zeta }}_h^{(k)}$, and ${\mathit{\xi }}_e^{(k)}.$

(ii)

Keeping the densities ${\mathit{\zeta }}_e$ and ${\mathit{\zeta }}_h$ fixed, we linearize the fifth equation of (23(23) $$\begin{array}{c}\hfill \left(\begin{array}{c}{\mathcal{A}}_1\\ {\mathcal{A}}_2\\ {\mathcal{A}}_3\\ {\mathcal{A}}_4\\ {\mathcal{A}}_5\end{array}\right)(r;{\mathit{\zeta }}_e)+\left(\begin{array}{c}{\mathcal{B}}_1\\ {\mathcal{B}}_2\\ {\mathcal{B}}_3\\ {\mathcal{B}}_4\\ {\mathcal{B}}_5\end{array}\right)(r;{\mathit{\xi }}_h)+\left(\begin{array}{c}{\mathcal{C}}_1\\ {\mathcal{C}}_2\\ {\mathcal{C}}_3\\ {\mathcal{C}}_4\\ {\mathcal{C}}_5\end{array}\right)(r;{\mathit{\zeta }}_h)+\left(\begin{array}{c}{\mathcal{D}}_1\\ {\mathcal{D}}_2\\ {\mathcal{D}}_3\\ {\mathcal{D}}_4\\ {\mathcal{D}}_5\end{array}\right)(r;{\mathit{\xi }}_e)=\left(\begin{array}{c}{\mathcal{F}}_1\\ {\mathcal{F}}_2\\ {\mathcal{F}}_3\\ {\mathcal{F}}_4\\ {\mathcal{F}}_5\end{array}\right),\end{array}$$(23) ), namely (25) $$\begin{array}{cc}& {\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})+({\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_e^{(k)}))(q)+{\mathcal{C}}_5(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\hfill \\ \hfill & +({\mathcal{C}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_h^{(k)}))(q)={\mathcal{F}}_5.\hfill \end{array}$$(25) We solve this equation for q and we update the radial function $r^{(k)}=r^{(k-1)}+q.$

The iteration stops when a suitable stopping criterion is satisfied.

Remark 1:

In order to take advantage of the available measurement data, we can also keep the overdetermined system (17(17) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{1}{{\widetilde{\mathit{ϵ}}}_1}\left(D_1-\frac{1}{2}\right){\mathit{\varphi }}_e-\frac{1}{{\widetilde{\mathit{ϵ}}}_0}{S}_0{\mathit{\psi }}_e& =e_3^{\mathit{inc}},\hfill \\ \hfill \mathit{\omega }N{D}_1{\mathit{\varphi }}_h+\frac{{\mathit{\beta }}_1}{{\widetilde{\mathit{ϵ}}}_1}\left(T{D}_1-\frac{1}{2}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\tau }}\right){\mathit{\varphi }}_e-\mathit{\omega }\left(N{S}_0-\frac{1}{2}\right){\mathit{\psi }}_h-\frac{{\mathit{\beta }}_0}{{\widetilde{\mathit{ϵ}}}_0}T{S}_0{\mathit{\psi }}_e& ={\mathit{\beta }}_0\frac{\mathit{\partial }{e}_3^{\mathit{inc}}}{\mathit{\partial }\mathit{\tau }},\hfill \\ \hfill \frac{1}{{\tilde{\mathit{\mu }}}_1}\left(D_1-\frac{1}{2}\right){\mathit{\varphi }}_h-\frac{1}{{\tilde{\mathit{\mu }}}_0}{S}_0{\mathit{\psi }}_h& =0,\hfill \\ \hfill \mathit{\omega }N{D}_1{\mathit{\varphi }}_e-\frac{{\mathit{\beta }}_1}{{\tilde{\mathit{\mu }}}_1}\left(T{D}_1-\frac{1}{2}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\tau }}\right){\mathit{\varphi }}_h-\mathit{\omega }\left(N{S}_0-\frac{1}{2}\right){\mathit{\psi }}_e+\frac{{\mathit{\beta }}_0}{{\tilde{\mathit{\mu }}}_0}T{S}_0{\mathit{\psi }}_h& ={\widetilde{\mathit{ϵ}}}_0\mathit{\omega }\frac{\mathit{\partial }{e}_3^{\mathit{inc}}}{\mathit{\partial }n}.\hfill \end{array}\end{array}$$(17) ) and () instead of (22e(22e) $$\begin{array}{cc}\hfill S^{\infty }{\mathit{\psi }}_e+S^{\infty }{\mathit{\psi }}_h& ={\widetilde{\mathit{ϵ}}}_0{e}^{\infty }+{\tilde{\mathit{\mu }}}_0{h}^{\infty },\hfill \end{array}$$(22e) ) and replace Equation (25(25) $$\begin{array}{cc}& {\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})+({\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_e^{(k)}))(q)+{\mathcal{C}}_5(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\hfill \\ \hfill & +({\mathcal{C}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_h^{(k)}))(q)={\mathcal{F}}_5.\hfill \end{array}$$(25) ) with(26) $$\begin{array}{c}\hfill \left(\begin{array}{c}{\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})\\ {\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\end{array}\right)q=\left(\begin{array}{c}{\mathcal{F}}_e\\ {\mathcal{F}}_h\end{array}\right)-\left(\begin{array}{c}{\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})\\ {\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\end{array}\right),\end{array}$$(26)

where now ${\mathcal{F}}_e={\widetilde{\mathit{ϵ}}}_0{e}^{\infty }$ and ${\mathcal{F}}_h={\tilde{\mathit{\mu }}}_0{h}^{\infty }.$

The Fréchet derivatives of the operators are calculated by formally differentiating their kernels with respect to r (27) $$\begin{array}{cc}\hfill (({\mathcal{A}}_5^{\prime }(r;\mathit{\zeta }))(q))(t)& =\frac{e^{i\mathit{\pi }/4}}{\sqrt{8\mathit{\pi }{\mathit{\kappa }}_0}}{\int }_0^{2\mathit{\pi }}{e}^{-i{\mathit{\kappa }}_0\widehat{\mathit{z}}(t)·\mathit{z}(s)}(-i{\mathit{\kappa }}_0\widehat{\mathit{z}}(t)·\mathit{q}(s)|{\mathit{z}}^{\prime }(s)|\hfill \\ \hfill & +\frac{{\mathit{z}}^{\prime }(s)·{\mathit{q}}^{\prime }(s)}{|{\mathit{z}}^{\prime }(s)|})\mathit{\zeta }(s)\mathrm{d}s.\hfill \end{array}$$(27)

Recall that ${\mathcal{A}}_5={\mathcal{C}}_5=S^{\infty }.$ If ${\mathit{\kappa }}_0^2$ is not an interior Neumann eigenvalue, then the operator ${\mathcal{A}}_5^{\prime }$ is injective [25]. Using similar arguments as in [30,36], we can relate the above iterative scheme to the classical Newton’s method.

The iterative scheme 3.1 can also be generalized to the case of multiple illuminations ${\mathbf{e}}_l^{\mathit{inc}},l=1,\dots ,L.$

Iterative Scheme 2:

[Multiple illuminations] Let $r^{(0)}$ be an initial approximation of the radial function. Then, in the kth iteration step:

(i)

We assume that we know $r^{(k-1)}$ and we solve the L subsystems (28) $$\begin{array}{cc}& \left(\begin{array}{c}{\mathcal{A}}_1\\ {\mathcal{A}}_2\\ {\mathcal{A}}_3\\ {\mathcal{A}}_4\end{array}\right)(r^{(k-1)};{\mathit{\zeta }}_{e,l})+\left(\begin{array}{c}{\mathcal{B}}_1\\ {\mathcal{B}}_2\\ {\mathcal{B}}_3\\ {\mathcal{B}}_4\end{array}\right)(r^{(k-1)};{\mathit{\xi }}_{h,l})+\left(\begin{array}{c}{\mathcal{C}}_1\\ {\mathcal{C}}_2\\ {\mathcal{C}}_3\\ {\mathcal{C}}_4\end{array}\right)(r^{(k-1)};{\mathit{\zeta }}_{h,l})\hfill \\ & +\left(\begin{array}{c}{\mathcal{D}}_1\\ {\mathcal{D}}_2\\ {\mathcal{D}}_3\\ {\mathcal{D}}_4\end{array}\right)(r^{(k-1)};{\mathit{\xi }}_{e,l})=\left(\begin{array}{c}{\mathcal{F}}_{1,l}\\ {\mathcal{F}}_{2,l}\\ {\mathcal{F}}_{3,l}\\ {\mathcal{F}}_{4,l}\end{array}\right),l=1,\dots ,L\hfill \end{array}$$(28) to obtain the densities ${\mathit{\zeta }}_{e,l}^{(k)},{\mathit{\xi }}_{h,l}^{(k)},{\mathit{\zeta }}_{h,l}^{(k)}$ and ${\mathit{\xi }}_{e,l}^{(k)}.$

(ii)

Then, keeping the densities fixed, we solve the overdetermined version of the linearized fifth equation of (23(23) $$\begin{array}{c}\hfill \left(\begin{array}{c}{\mathcal{A}}_1\\ {\mathcal{A}}_2\\ {\mathcal{A}}_3\\ {\mathcal{A}}_4\\ {\mathcal{A}}_5\end{array}\right)(r;{\mathit{\zeta }}_e)+\left(\begin{array}{c}{\mathcal{B}}_1\\ {\mathcal{B}}_2\\ {\mathcal{B}}_3\\ {\mathcal{B}}_4\\ {\mathcal{B}}_5\end{array}\right)(r;{\mathit{\xi }}_h)+\left(\begin{array}{c}{\mathcal{C}}_1\\ {\mathcal{C}}_2\\ {\mathcal{C}}_3\\ {\mathcal{C}}_4\\ {\mathcal{C}}_5\end{array}\right)(r;{\mathit{\zeta }}_h)+\left(\begin{array}{c}{\mathcal{D}}_1\\ {\mathcal{D}}_2\\ {\mathcal{D}}_3\\ {\mathcal{D}}_4\\ {\mathcal{D}}_5\end{array}\right)(r;{\mathit{\xi }}_e)=\left(\begin{array}{c}{\mathcal{F}}_1\\ {\mathcal{F}}_2\\ {\mathcal{F}}_3\\ {\mathcal{F}}_4\\ {\mathcal{F}}_5\end{array}\right),\end{array}$$(23) ) $$\begin{array}{c}\hfill \left(\begin{array}{c}{\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_{e,1}^{(k)}+{\mathit{\zeta }}_{h,1}^{(k)})\\ {\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_{e,2}^{(k)}+{\mathit{\zeta }}_{h,2}^{(k)})\\ ⋮\\ {\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_{e,l}^{(k)}+{\mathit{\zeta }}_{h,l}^{(k)})\end{array}\right)q=\left(\begin{array}{c}{\mathcal{F}}_{5,1}-{\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_{e,1}^{(k)}+{\mathit{\zeta }}_{h,1}^{(k)})\\ {\mathcal{F}}_{5,2}-{\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_{e,2}^{(k)}+{\mathit{\zeta }}_{h,2}^{(k)})\\ ⋮\\ {\mathcal{F}}_{5,L}-{\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_{e,l}^{(k)}+{\mathit{\zeta }}_{h,l}^{(k)})\end{array}\right)\end{array}$$ for q and we update the radial function $r^{(k)}=r^{(k-1)}+q.$

The iteration stops when a suitable stopping criterion is satisfied.

4. Numerical implementation

In this section, we present numerical examples that illustrate the applicability of the proposed method. We use quadrature rules for integrating the singularities considering trigonometric interpolation. The convergence and error analysis are given in [37,38]. Then, the system of integral equations is solved using the Nyström method. The parametrized forms of the integral operators are presented in [8, Section 4]. We approximate the smooth kernels with the trapezoidal rule and the singular ones with the well-known quadratures rules [38].

In the following examples, we consider two different boundary curves. A peanut-shaped and an apple-shaped boundary with radial function$$r(t)={(0.5{cos}^{2}t+0.15{sin}^{2}t)}^{1/2},t\in [0,2\mathit{\pi }],$$

and$$r(t)=\frac{0.45+0.3cost-0.1sin2t}{1+0.7cost},t\in [0,2\mathit{\pi }],$$

respectively.

To avoid an inverse crime, we construct the simulated far-field data using the numerical scheme (12(12) $$\begin{array}{c}\hfill ({\mathbf{D}}_0+{\mathbf{K}}_0)\left(\begin{array}{c}{\mathit{\varphi }}_0\\ {\mathit{\psi }}_0\end{array}\right)={\mathbf{b}}_0,\end{array}$$(12) ) and considering double amount of quadrature points compared to the inverse problem. We approximate the radial function q by a trigonometric polynomial of the form$$q(t)\approx \sum _{k=0}^m{a}_{k}coskt+\sum _{k=1}^m{b}_{k}sinkt,t\in [0,2\mathit{\pi }],$$

and we consider 2n equidistant points $t_j=j\mathit{\pi }/n,j=0,\dots ,2n-1.$ The well-posed subsystem (24(24) $$\begin{array}{cc}& \left(\begin{array}{c}{\mathcal{A}}_1\\ {\mathcal{A}}_2\\ {\mathcal{A}}_3\\ {\mathcal{A}}_4\end{array}\right)(r^{(k-1)};{\mathit{\zeta }}_e)+\left(\begin{array}{c}{\mathcal{B}}_1\\ {\mathcal{B}}_2\\ {\mathcal{B}}_3\\ {\mathcal{B}}_4\end{array}\right)(r^{(k-1)};{\mathit{\xi }}_h)+\left(\begin{array}{c}{\mathcal{C}}_1\\ {\mathcal{C}}_2\\ {\mathcal{C}}_3\\ {\mathcal{C}}_4\end{array}\right)(r^{(k-1)};{\mathit{\zeta }}_h)\hfill \\ \hfill & +\left(\begin{array}{c}{\mathcal{D}}_1\\ {\mathcal{D}}_2\\ {\mathcal{D}}_3\\ {\mathcal{D}}_4\end{array}\right)(r^{(k-1)};{\mathit{\xi }}_e)=\left(\begin{array}{c}{\mathcal{F}}_1\\ {\mathcal{F}}_2\\ {\mathcal{F}}_3\\ {\mathcal{F}}_4\end{array}\right),\hfill \end{array}$$(24) ) does not require any special treatment. The ill-posed linearized far-field Equation (25(25) $$\begin{array}{cc}& {\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})+({\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_e^{(k)}))(q)+{\mathcal{C}}_5(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\hfill \\ \hfill & +({\mathcal{C}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_h^{(k)}))(q)={\mathcal{F}}_5.\hfill \end{array}$$(25) ) is solved by Tikhonov regularization. We rewrite (25(25) $$\begin{array}{cc}& {\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})+({\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_e^{(k)}))(q)+{\mathcal{C}}_5(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\hfill \\ \hfill & +({\mathcal{C}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_h^{(k)}))(q)={\mathcal{F}}_5.\hfill \end{array}$$(25) ) as:(29) $$\begin{array}{c}\hfill ({\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}^{(k)}))(q)={\mathcal{F}}_5-{\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}^{(k)}),\end{array}$$(29)

for ${\mathit{\zeta }}^{(k)}:={\mathit{\zeta }}_e^{(k)}+{\mathit{\zeta }}_h^{(k)},$ and we decompose (27(27) $$\begin{array}{cc}\hfill (({\mathcal{A}}_5^{\prime }(r;\mathit{\zeta }))(q))(t)& =\frac{e^{i\mathit{\pi }/4}}{\sqrt{8\mathit{\pi }{\mathit{\kappa }}_0}}{\int }_0^{2\mathit{\pi }}{e}^{-i{\mathit{\kappa }}_0\widehat{\mathit{z}}(t)·\mathit{z}(s)}(-i{\mathit{\kappa }}_0\widehat{\mathit{z}}(t)·\mathit{q}(s)|{\mathit{z}}^{\prime }(s)|\hfill \\ \hfill & +\frac{{\mathit{z}}^{\prime }(s)·{\mathit{q}}^{\prime }(s)}{|{\mathit{z}}^{\prime }(s)|})\mathit{\zeta }(s)\mathrm{d}s.\hfill \end{array}$$(27) ) as:(30) $$\begin{array}{c}\hfill (({\mathcal{A}}_5^{\prime }(r;\mathit{\zeta }))(q))(t)=(({\mathcal{G}}_1(r;\mathit{\zeta }))(q))(t)+(({\mathcal{G}}_2(r;\mathit{\zeta }))(q^{\prime }))(t),\end{array}$$(30)

where$$\begin{array}{cc}\hfill (({\mathcal{G}}_1(r;\mathit{\zeta }))(q))(t)& :=\frac{e^{i\mathit{\pi }/4}}{\sqrt{8\mathit{\pi }{\mathit{\kappa }}_0}}{\int }_0^{2\mathit{\pi }}{e}^{-i{\mathit{\kappa }}_0\widehat{\mathit{z}}(t)·\mathit{z}(s)}\left[-i{\mathit{\kappa }}_0\widehat{\mathit{z}}(t)·(coss,sins)|{\mathit{z}}^{\prime }(s)|\right.\hfill \\ \hfill & \left.+\frac{{\mathit{z}}^{\prime }(s)·(-sins,coss)}{|{\mathit{z}}^{\prime }(s)|}\right]\mathit{\zeta }(s)q(s)\mathrm{d}s,\hfill \\ \hfill (({\mathcal{G}}_2(r;\mathit{\zeta }))(q^{\prime }))(t)& :=\frac{e^{i\mathit{\pi }/4}}{\sqrt{8\mathit{\pi }{\mathit{\kappa }}_0}}{\int }_0^{2\mathit{\pi }}{e}^{-i{\mathit{\kappa }}_0\widehat{\mathit{z}}(t)·\mathit{z}(s)}\frac{{\mathit{z}}^{\prime }(s)·(coss,sins)}{|{\mathit{z}}^{\prime }(s)|}\mathit{\zeta }(s)q^{\prime }(s)\mathrm{d}s.\hfill \end{array}$$

We replace the derivative of q by the derivative of the trigonometric interpolation polynomial$$q^{\prime }(t)\approx \sum _{j=0}^{2n-1}\mathbf{Q}(t,t_j)q(t_j),$$

with weight$$\mathbf{Q}(t_k,t_j)=\frac{1}{2}{(-1)}^{k-j}cot\frac{t_k-t_j}{2},k\ne j,k=0,\dots ,2n-1.$$

Then, at the kth step we minimize the Tikhonov functional of the discretized equation$${\Vert \mathbf{A}\mathbf{T}\mathbf{x}-\mathbf{b}\Vert }_2^2+\mathit{\lambda }{\Vert \mathbf{x}\Vert }_p^p,\mathit{\lambda }>0,$$

where $\mathbf{x}\in R^{(2m+1)\times 1}$ is the vector with the unknowns coefficients $a_0,\dots ,a_m,$ $b_1,\dots ,b_m$ of the radial function, and $\mathbf{A}\in C^{2n\times 2n},\mathbf{b}\in C^{2n\times 1}$ are given by:$$\begin{array}{cc}\hfill {\mathbf{A}}_{\mathit{kj}}& ={\mathbf{M}}^{{\mathcal{G}}_1}(t_k,t_j)+{\mathbf{M}}^{{\mathcal{G}}_2}(t_k,t_j)\mathbf{Q}(t_k,t_j),\hfill \\ \hfill {\mathbf{b}}_k& ={\mathcal{F}}_5(t_k)-({\mathbf{M}}^{{\mathcal{A}}_5}\mathit{\zeta })(t_k),\hfill \end{array}$$

for $k,j=0,\dots ,2n-1.$ The multiplication matrix $\mathbf{T}\in R^{2n\times (2m+1)}$ stands for the trigonometric functions of the approximated radial function and is given by:$$\begin{array}{c}\hfill {\mathbf{T}}_{\mathit{kj}}=\left\{\begin{array}{cc}cos\frac{kj\mathit{\pi }}{n},\hfill & k=0,\dots ,2n-1,j=0,\dots ,m\hfill \\ sin\frac{k(j-m)\mathit{\pi }}{n},\hfill & k=0,\dots ,2n-1,j=m+1,\dots ,2m\hfill \end{array}\right.\end{array}$$

Here, $p\ge 0$ defines the corresponding Sobolev norm. Since q is real valued, we solve the following regularized equation:(31) $$\begin{array}{cc}& \left({\mathbf{T}}^{\top }\left(\mathfrak{R}{(\mathbf{A})}^{\top }\mathfrak{R}(\mathbf{A})+\mathfrak{I}{(\mathbf{A})}^{\top }\mathfrak{I}(\mathbf{A})\right)\mathbf{T}+{\mathit{\lambda }}_k{\mathbf{I}}_p\right)\mathbf{x}\hfill \\ \hfill & ={\mathbf{T}}^{\top }\left(\mathfrak{R}{(\mathbf{A})}^{\top }\mathfrak{R}(\mathbf{b})+\mathfrak{I}{(\mathbf{A})}^{\top }\mathfrak{I}(\mathbf{b})\right),\hfill \end{array}$$(31)

on the kth step, where the matrix ${\mathbf{I}}_p\in R^{(2m+1)\times (2m+1)}$ corresponds to the Sobolev $H^p$ penalty term. We solve (31(31) $$\begin{array}{cc}& \left({\mathbf{T}}^{\top }\left(\mathfrak{R}{(\mathbf{A})}^{\top }\mathfrak{R}(\mathbf{A})+\mathfrak{I}{(\mathbf{A})}^{\top }\mathfrak{I}(\mathbf{A})\right)\mathbf{T}+{\mathit{\lambda }}_k{\mathbf{I}}_p\right)\mathbf{x}\hfill \\ \hfill & ={\mathbf{T}}^{\top }\left(\mathfrak{R}{(\mathbf{A})}^{\top }\mathfrak{R}(\mathbf{b})+\mathfrak{I}{(\mathbf{A})}^{\top }\mathfrak{I}(\mathbf{b})\right),\hfill \end{array}$$(31) ) using the conjugate gradient method. We update the regularization parameter in each iteration step k by:$${\mathit{\lambda }}_k={\mathit{\lambda }}_0{\left(\frac{2}{3}\right)}^{k-1},k=1,2,\dots$$

for some given initial parameter ${\mathit{\lambda }}_0>0.$ To test the stability of the iterative method against noisy data, we add also noise to the far-field patterns with respect to the $L^2-$norm$$e_{\mathit{\delta }}^{\infty }=e^{\infty }+{\mathit{\delta }}_1\frac{\Vert e^{\infty }{\Vert }_2}{{\Vert u\Vert }_2}u,h_{\mathit{\delta }}^{\infty }=h^{\infty }+{\mathit{\delta }}_2\frac{\Vert h^{\infty }{\Vert }_2}{{\Vert v\Vert }_2}v,$$

for some given noise levels, ${\mathit{\delta }}_1,{\mathit{\delta }}_2$ where $u=u_1+\mathrm{i}{u}_2,v=v_1+\mathrm{i}{v}_2,$ for $u_1,u_2,v_1,v_2\in R$ normally distributed random variables.

Figure 2. Reconstruction of a peanut-shaped boundary for two incident fields, frequency $\mathit{\omega }=2.5,$ for exact data (left) and data with $5\%$ noise (right).

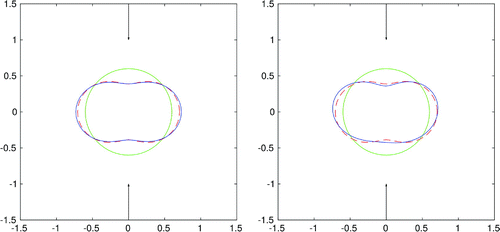
Already in simpler cases [30], the knowledge of the far-field patterns for one incident wave is not enough to produce satisfactory reconstructions. Thus, we will also use multiple incident directions. To do so, we have to consider different values of the polar angle $\mathit{\varphi }$ since in $R^2,$ as we see from (6(6) $$\begin{array}{c}\hfill \begin{array}{c}\hfill e_3^{\mathit{inc}}(\mathit{x})=\frac{1}{\sqrt{{\mathit{ϵ}}_0}}sin\mathit{\theta }{e}^{i{\mathit{\kappa }}_0(xcos\mathit{\varphi }+ysin\mathit{\varphi })},h_3^{\mathit{inc}}(\mathit{x})=0.\end{array}\end{array}$$(6) ), corresponds to the incident direction $\mathbf{d}=(cos\mathit{\varphi },sin\mathit{\varphi })$. We set$${\mathbf{d}}_l=\left(cos{\mathit{\varphi }}_l,sin{\mathit{\varphi }}_l\right),\text{where}{\mathit{\varphi }}_l=\frac{2\mathit{\pi }l}{L},\text{for}l=1,\dots ,L.$$

4.1. Numerical results

We present reconstructions for different boundary curves, different number of incident directions and initial guesses for exact and perturbed far-field data. In all figures the initial guess is a circle with radius $r_0,$ a green solid line, the exact curve is represented by a dashed red line and the reconstructed by a solid blue line. The arrows denote the directions of the incoming incident fields.

We use $n=64$ collocation points for the direct problem and $n=32$ for the inverse. In the first five examples, we set the exterior parameters $({\mathit{ϵ}}_0,{\mathit{\mu }}_0)=(1,1)$ and the interior $({\mathit{ϵ}}_1,{\mathit{\mu }}_1)=(2,2).$ We set $\mathit{\theta }=\mathit{\pi }/3$ and ${\mathit{\lambda }}_0\in [0.5,0.8]$ as the initial regularization parameter.

Figure 3. Reconstruction of a peanut-shaped boundary for four incident fields, frequency $\mathit{\omega }=2.5,$ noisy data ($5\%$ noise), with initial guess $r_0=0.6$ (left) and $r_0=1$ (right).

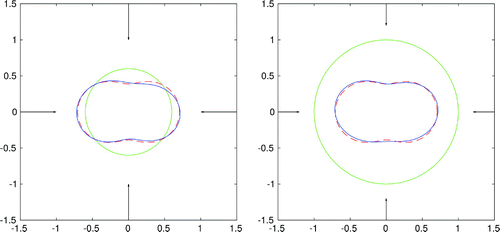
Figure 4. Reconstruction of a peanut-shaped boundary for four incident fields, $m=5$ coefficients, frequency $\mathit{\omega }=2,$ for exact data (left) and data with $3\%$ noise (right).

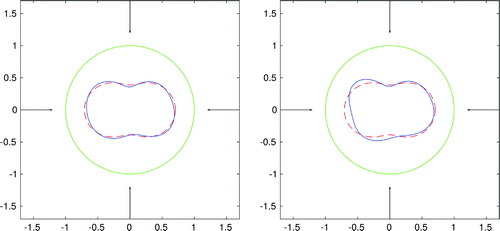
In the first three examples, we consider the peanut-shaped boundary. In the first example, the regularized Equation (31(31) $$\begin{array}{cc}& \left({\mathbf{T}}^{\top }\left(\mathfrak{R}{(\mathbf{A})}^{\top }\mathfrak{R}(\mathbf{A})+\mathfrak{I}{(\mathbf{A})}^{\top }\mathfrak{I}(\mathbf{A})\right)\mathbf{T}+{\mathit{\lambda }}_k{\mathbf{I}}_p\right)\mathbf{x}\hfill \\ \hfill & ={\mathbf{T}}^{\top }\left(\mathfrak{R}{(\mathbf{A})}^{\top }\mathfrak{R}(\mathbf{b})+\mathfrak{I}{(\mathbf{A})}^{\top }\mathfrak{I}(\mathbf{b})\right),\hfill \end{array}$$(31) ) is solved with $L^2$ penalty term, meaning $p=0$ and $m=3$ coefficients. We solve Equation (26(26) $$\begin{array}{c}\hfill \left(\begin{array}{c}{\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})\\ {\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\end{array}\right)q=\left(\begin{array}{c}{\mathcal{F}}_e\\ {\mathcal{F}}_h\end{array}\right)-\left(\begin{array}{c}{\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})\\ {\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\end{array}\right),\end{array}$$(26) ) for different incident directions. The reconstructions for $\mathit{\omega }=2.5$ and $r_0=0.6$ are presented in Figure 2 for two incident fields with directions ${\mathbf{d}}_{l+1/2}.$ On the left picture, we see the reconstructed curve for exact data and 9 iterations and on the right picture for noisy data with ${\mathit{\delta }}_1={\mathit{\delta }}_2=5\%$ and 14 iterations. In the second example, we consider Equation (25(25) $$\begin{array}{cc}& {\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})+({\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_e^{(k)}))(q)+{\mathcal{C}}_5(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\hfill \\ \hfill & +({\mathcal{C}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_h^{(k)}))(q)={\mathcal{F}}_5.\hfill \end{array}$$(25) ), four incident fields, noisy data ${\mathit{\delta }}_1={\mathit{\delta }}_2=5\%$ and we keep all the parameters as before. The reconstructions for $r_0=0.6$ and 14 iterations are shown in the left picture of Figure 3, and for $r_0=1$ and 20 iterations in the right one. We set $m=5$ and $p=1$ ($H^1$ penalty term) in the third example. The results for $r_0=1$ and four incident fields are shown in Figure 4. Here, $\mathit{\omega }=2$ and we use Equation (26(26) $$\begin{array}{c}\hfill \left(\begin{array}{c}{\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})\\ {\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\end{array}\right)q=\left(\begin{array}{c}{\mathcal{F}}_e\\ {\mathcal{F}}_h\end{array}\right)-\left(\begin{array}{c}{\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})\\ {\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\end{array}\right),\end{array}$$(26) ). We need 26 iterations for the exact data and 30 iterations for the noisy data (${\mathit{\delta }}_1={\mathit{\delta }}_2=3\%$).

Figure 5. Reconstruction of an apple-shaped boundary for four incident fields, frequency $\mathit{\omega }=3,$ exact data, with initial guess $r_0=0.5$ (left) and $r_0=1$ (right).

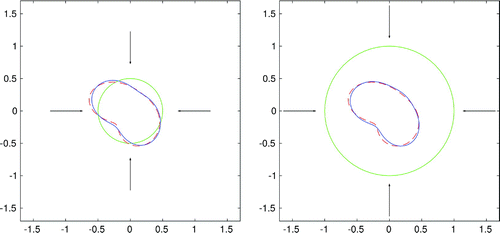
Figure 6. Reconstruction of an apple-shaped boundary for four incident fields, frequency $\mathit{\omega }=3,$ data with $3\%$ noise, for three (left) and four (right) incident fields.

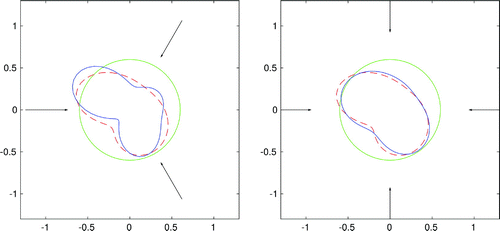
In the next two examples we consider the apple-shaped boundary, $H^1$ penalty term, $\mathit{\omega }=3$ and $m=3$ coefficients. In the fourth example, we consider Equation (25(25) $$\begin{array}{cc}& {\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})+({\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_e^{(k)}))(q)+{\mathcal{C}}_5(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\hfill \\ \hfill & +({\mathcal{C}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_h^{(k)}))(q)={\mathcal{F}}_5.\hfill \end{array}$$(25) ), noise-free data and four incident fields in order to examine the dependence of the iterative scheme on the initial radial guess. On the left picture of Figure 5, we see the reconstructed curve for $r_0=0.5$ after 13 iterations and on the right picture for $r_0=1$ after 20 iterations. In the fifth example, we consider ${\mathit{\delta }}_1={\mathit{\delta }}_2=3\%$ noise and $r_0=0.6.$ Figure 6 shows the improvement of the reconstruction for more incident fields. On the left picture we see the results for three incident fields, Equation (26(26) $$\begin{array}{c}\hfill \left(\begin{array}{c}{\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})\\ {\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\end{array}\right)q=\left(\begin{array}{c}{\mathcal{F}}_e\\ {\mathcal{F}}_h\end{array}\right)-\left(\begin{array}{c}{\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})\\ {\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\end{array}\right),\end{array}$$(26) ) and seven iterations and the reconstructed curve for four incident fields, Equation (25(25) $$\begin{array}{cc}& {\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})+({\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_e^{(k)}))(q)+{\mathcal{C}}_5(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\hfill \\ \hfill & +({\mathcal{C}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_h^{(k)}))(q)={\mathcal{F}}_5.\hfill \end{array}$$(25) ) and 15 iterations is shown on the right picture.

In the last example we consider an electrically larger object, meaning we set $({\mathit{ϵ}}_0,{\mathit{\mu }}_0)=(3,3)$ and $\mathit{\omega }=7,$ resulting to a seven times larger (electrically) scatterer compared to the previous examples. We choose $({\mathit{ϵ}}_1,{\mathit{\mu }}_1)=(9,1)$ such that the condition ${\mathit{\mu }}_1{\mathit{ϵ}}_1>{\mathit{\mu }}_0{\mathit{ϵ}}_0{cos}^2\mathit{\theta }$ is satisfied. To account also for different oblique directions we set $\mathit{\theta }=\mathit{\pi }/10.$ For $m=3$ and data with $3\%$ noise, we present the reconstructions in Figure 7. We consider for both boundary curves the same initial guess $r_0=0.6.$ The results on the left picture are for two incident fields, considering Equation (26(26) $$\begin{array}{c}\hfill \left(\begin{array}{c}{\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})\\ {\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\end{array}\right)q=\left(\begin{array}{c}{\mathcal{F}}_e\\ {\mathcal{F}}_h\end{array}\right)-\left(\begin{array}{c}{\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})\\ {\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\end{array}\right),\end{array}$$(26) ) and 35 iterations. On the right picture we present the reconstruction for four incident fields, Equation (25(25) $$\begin{array}{cc}& {\mathcal{A}}_5(r^{(k-1)};{\mathit{\zeta }}_e^{(k)})+({\mathcal{A}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_e^{(k)}))(q)+{\mathcal{C}}_5(r^{(k-1)};{\mathit{\zeta }}_h^{(k)})\hfill \\ \hfill & +({\mathcal{C}}_5^{\prime }(r^{(k-1)};{\mathit{\zeta }}_h^{(k)}))(q)={\mathcal{F}}_5.\hfill \end{array}$$(25) ) and 13 iterations.

Figure 7. Reconstruction of a peanut-shaped boundary for two incident fields (left) and an apple-shaped boundary for four incident fields (right). Here, we use $\mathit{\theta }=\mathit{\pi }/10,\mathit{\omega }=7$ and data with $3\%$ noise.

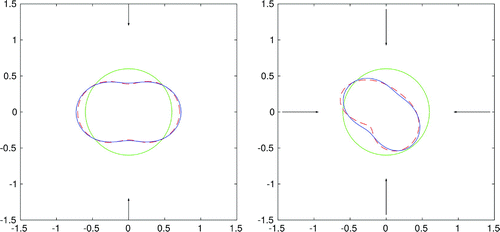
To conclude, our examples have shown the feasibility of the proposed iterative scheme and the stability against noisy data. However, this method can only be applied to objects with smooth boundaries. In addition, the proposed method performs poorly for only one incident field which is the case also in the acoustic regime. The main reason is that we miss information since we linearize only the far-field equation. Thus, we had to consider few incident illuminations which improve considerably the reconstructions. The initial guess plays also an important role in this scheme.

Notes

No potential conflict of interest was reported by the authors.