The use of the scaling property in a frontier analysis of a system of equations

ABSTRACT

This article presents a one-stage efficiency frontier analysis based on the scaling property. This type of analysis is a not very often applied in empirical work in spite of its nice features. Due to the scaling property the influence of exogenous (managerial) variables on efficiency can be modelled and estimated in one stage. It also opens the possibility of estimating a system of equations, consisting of a cost function and the corresponding cost share equations. The model is applied to a unique data set of Dutch secondary education school boards in the period 2007–10, not only consisting of regular data on cost, inputs and outputs, but also of specific data on operational management. The model provides reliable and plausible estimates for the cost efficiency, scale elasticity, and technical change. Average cost efficiency is about 96%. Economies of scale prevail for school boards with size less than 0.8 times average size, whereas annual productivity growth is 2.2% on average.

KEYWORDS:

• Cost frontier analysis
• scaling property
• system of equations
• school boards
• education

JEL CLASSIFICATION:

• C51
• C54
• D24
• I22

I. Introduction

Stochastic frontier analysis (SFA) is a very popular method to establish the efficiency scores of firms. The method, which was developed by Aigner et al. (1977) and Meeusen and Van den Broeck (1977), has been extensively applied to firms in various industries to get an insight into the relative efficiency of individual firms. The method has also been applied to compare the performance of departments within firms, and even to compare the performance of countries. Extensive reviews of the SFA approach can be found in various publications (see e.g. Blank 2000; Coelli et al. 2005; Fried, Lovell, and Schmidt 2008; Kumbhakar and Lovell 2000; Parmeter and Kumbhakar 2014).

Despite its popularity, the method has provoked severe criticism. The critics focus on the required functional specification of the model and the distributional assumptions about the efficiency component. Less criticism is voiced about the fact that the method can hardly be applied to systems of equations that can be derived from duality theory, in spite of the fact that these system of equations are applied for quite some time (Schmidt and Knox Lovell 1979; Schmidt and Lovell 1980). Complicated solutions have been provided by Kumbhakar and Tsionas (2005), based on Bayesian techniques or through the reformulation of the model (Blank and Eggink 2004; Kumbhakar 1997; Maietta 2002). Almost all empirical applications are therefore limited to single equation models.

Another criticism regards the strong assumption that efficiency can be derived from components that follow a one-sided distribution. This is a very questionable assumption. There are plenty of reasons why measurement errors can also have a one-sided distribution. A common failure is that missing values are interpreted as zeroes and that subtotals are an underestimate of the true value of a variable. This issue has not been thoroughly addressed in literature. For example, in deriving a crime index, Chaudhuri, Chowdhury, and Kumbhakar (2015) explicitly apply SFA with respect to the underreporting of sexual crimes.

As such, efficiency measures have only limited meaning. Only when efficiency scores can be related to managerial or policy issues, is efficiency measurement meaningful. Searching for explanations is therefore a relevant part of efficiency research. Common practice is to derive efficiency scores and then regress the efficiency scores on a number of explanatory managerial variables (two-stage estimation). This approach has some serious drawbacks, however, since managerial variables can be correlated to other variables in the model. Estimates in the first stage might be biased due to the omitted variable problem distribution (Kumbhakar and Lovell 2000; Schmidt 2011; Wang and Schmidt 2002). Solutions have been provided ever since, for instance by Battese and Coelli (1995), based on the availability of panel data. This method is a complex technique with some serious computational problems.

An alternative is to use the scaling property, which has not been explored widely in applications, but has been mentioned for quite a while (see e.g. Simar, Lovell, and Vanden Eeckaut 1994). The scaling property states that a non-negative random variable u_i, which depends on a set of exogenous variables, can be written as the product of a function of these exogenous variables and a non-negative random variable whose distribution does not involve exogenous factors (Alvarez et al. 2006). It leads to a model specification that can easily be estimated with non-linear least squares (NLLS) and without any distributional assumptions about the efficiency component. A more advanced approach, with endogenous efficiency determinants, can be found in Amsler, Prokhorov, and Schmidt (2017). Since we assume exogenous efficiency determinants we can avoid the complexity mentioned in that article.

Although the use of the scaling property in efficiency measurement has some major advantages, the approach has not been applied on a large scale, and certainly not in the case of a system of equations model, such as a cost function model. This paper fills that gap by demonstrating the benefits of such an approach. In addition to the above-mentioned benefits, the suggested approach provides more accurate parameter estimates (due to extra information in the share equations) and mitigates the Greene problem (Bauer 1990).

A number of authors emphasize the major advantages of using the scaling property for efficiency measurement, particularly the advantage of directly incorporating exogenous influences at the first stage, the ease of estimation by NLLS, and the relaxation of the requirement of a priori distributional assumptions (Alvarez et al. 2006; Schmidt 2011; Wang and Schmidt 2002).

The model is applied to a dataset of Dutch secondary education schools in the period 2007–10. Whereas in the Netherlands data on costs, outputs, and inputs of secondary schools are publicly accessible, data on operational management are rather scarce. However due to a special project that has been conducted for the ministry of Education, data on operational management have been collected for a brief period of time (2007–10). By matching these data with the regular data on costs, outputs and inputs a rather unique data set could be constructed. These data include, amongst other variables, a number of variables related to operational management that can be included in the scaling function. Examples of operational management variables are management experience, teaching staff experience and average school size. Since the data set also comprises of a substantial number of observations it fits the purpose of this paper very well.

There is an extensive literature on school efficiency (Agasisti and Gralka 2019; Barbetta and Turati 2003; Grosskopf, Hayes, and Taylor 2009; Haelermans and Blank 2012; Haelermans and Ruggiero 2013; Henderson, Simar, and Wang 2017; Millimet and Collier 2008; Ni 2009; Veiderpass and McKelvey 2016), and it is beyond the scope of this article to present an overview or comparison of the existing research. For an excellent (a bit dated) review of efficiency literature on schools, I refer to the dissertation of Haelermans (Haelermans 2012). In particular I also wish to refer to a paper of Marconi and Ritzen (2015), that also explicitly focuses on determinants of (university) efficiency scores.

The outline of the paper is as follows. First, we focus on the methodological aspects and derive the model. Second, we discuss the check and manipulation of the available data. Then we discuss the results of the estimation and present the relevant economic outcomes. In the final section, we summarize and discuss the major findings.

II. Methodology

In order to answer the research questions empirically, this study uses a cost model. A cost model consists of a cost function and corresponding cost share functions. The cost function establishes a link between the minimum cost on the one hand and the delivery of services and the prices of the resources used on the other. The cost share functions establish a link between the cost share of a specific resource used (e.g., teachers) on the one hand, and the production and prices of the resources used on the other.

The unobserved minimal cost $C^{\ast }$ can be written as a function of services produced (y), exogenous resource prices (w) and technical change (t). For reasons of convenience we transformed the variables into logarithms.

(1) $ln\left(C^{\ast }\right)=c\left(ln\left(y\right),ln\left(w\right),t\right)$(1)

For an empirical application the model is transformed into actual cost by adding a two-sided error representing misspecifications and measurement errors and a one-sided error reflecting cost efficiency whose distribution depends on z . The vector z is a set of variables explaining cost efficiency. So actual cost C can be represented as follows:

(2) $ln\left(C\right)=c\left(ln\left(y\right),ln\left(w\right),t\right)+v+u\left(z\right)$(2)

Where $u\left(z\right)\ge 0$, and v is $N\left(0,{\sigma }_v^2\right)$ and is independent of ln(y), ln(w), and $v$. In this framework, there is a whole range of possibilities for the specification of the cost efficiency term u(z). A common way is to specify a one-sided distribution for u, such as the half-normal or truncated normal and distribution, and let the parameters of the distribution depend on z. From this, a joint distribution with the normal distributed error term is derived, as is the likelihood function. In addition to the fact that we are dealing here with complex mathematical derivations, the maximum likelihood function often fails to converge. There is an alternative that makes life less complicated and also provides some new opportunities to incorporate additional information through cost shares, which will be explained later on. The alternative is based on the scaling property (Simar, Lovell, and Vanden Eeckaut 1994), which states that the efficiency term can be written as:

(3) $u\left(z,\delta \right)=h\left(z,\delta \right)u^{\ast }$(3)

Where $h\left(z,\delta \right)\ge 0$ (scaling function), $\delta$ a vector of parameters and $u^{\ast }$ (basic distribution) has a distribution that does not depend on $z$. An appealing candidate for the scaling function is $h\left(z,\delta \right)=\mathrm{e}\mathrm{x}\mathrm{p}\left(z^{\prime }\delta \right)$ and the basic distribution is$N(0,{\sigma }^2{)}^{+}$. An interesting feature of the scaling property is that it enables estimation of the parameters without having to specify the basic distribution (Kumbhakar and Lovell 2000; Schmidt 2011; Wang and Schmidt 2002). The parameters can therefore be estimated by nonlinear least squares.

The scaling function can accommodate all types of variables as long as they are uncorrelated with the error term. This means that it can also include variables that are already part of the basic cost function (2). This implies that, theoretically, we would be able to separate the effect of the production on minimal cost and the effect on the cost efficiency. Interesting candidates for the scaling function are the resource prices. From Shephard’s lemma, we know that from a regular cost function the optimal cost share $S_n^{\ast }=\frac{\mathrm{\partial }ln{C}^{\ast }}{\mathrm{\partial }ln{w}_n}$.

For an empirical application the optimal cost share equations are transformed into actual cost share equations by adding a two-sided error representing misspecifications and measurement errors.

(4) $S_n=\frac{\mathrm{\partial }ln{C}^{\ast }}{\mathrm{\partial }ln{w}_n}+v_n$(4)

Where:

S_n = cost share of resource n;

w_n = price of resource n;

v_n = error term of cost share n.

Further we assume that we can write the cost efficiency component as:

(5) $h\left(z,w,\delta \right)=\mathrm{e}\mathrm{x}\mathrm{p}\left(z^{\prime }{\delta }_z+ln{w}^{\prime }{\delta }_w\right)$(5)

Where:

$h\left(z,w,\delta \right)$ = scaling function;

$z$ = vector of exogenous variables;

$w$ = vector of resource prices;

$\delta$ = vector of parameters to be estimated.

In literature some alternative specifications to (5) are discussed. Further note that we included resource prices as well in the efficiency component for reasons mentioned earlier. Then we can write the share equations as:

(6) $S_n=\frac{\mathrm{\partial }ln{C}^{\ast }}{\mathrm{\partial }ln{w}_n}+{\delta }_{w_n}exp\left(z^{\prime }{\delta }_z+ln{w}^{\prime }{\delta }_w\right)+v_n$(6)

Which can be rewritten as:

(7) $S_n=\frac{\mathrm{\partial }ln{C}^{\ast }}{\mathrm{\partial }ln{w}_n}+{\delta }_{w_n}h\left(z,w,\delta \right)+v_n$(7)

Implying that a part (${\delta }_{w_n}$) of the cost inefficiency component can be attributed to cost share n. In order to guarantee that the cost shares sum up to 1, the following restriction must hold:

(8) $\sum _n{\delta }_{w_n}=0$(8)

From the cost model, various economic relationships are derived. These include the following relationships:

• Cost efficiency;

• Economies of scale;

• Technical change.

The cost efficiency indicates how an educational institution is performing compared to the best-practice settings, where 100% represents a score corresponding to the best-practice setting:

(9) $\widehat{CE}=exp\left[-h\left(z,w,\hat{\delta }\right)\right]$(9)

Scale effects are expressed in the cost flexibility, a number close to 1. A value of less than 1 indicates that the costs are rising more slowly than production (economies of scale). In that situation, scaling leads to lower average costs. For a value greater than 1, it obviously implies exactly the opposite (diseconomies of scale). Upscaling then leads to average cost enhancements.

Technical change is derived from the year-on-year changes in costs, after they have been adjusted for changes in production, prices of resources used, and operational management of individual institutions. Technical change is due to technological, institutional, and social changes, and can be derived from the terms including year dummies or trend variables.

III. Data

The model is applied to a set of Dutch secondary education boards for the years 2007–10. In the following sections, a brief description of the data on production, resources, and other characteristics is presented. A more elaborated discussion can be found in Blank (2015).

Production

The different types of schools in secondary education require different educational processes and consequently lead to different costs. For example, a teacher for students in the final year of pre-academic education, is generally more expensive than a teacher for students in the first year of vocational training. Therefore, the production cannot be captured in one number. Production indicators are based on the different types of education and grades. We therefore distinguish:

• Grades 1 and 2 all types of education (and specialized categories);

• Grades 3 and 4 vmbo (vocational training);

• Grades 3 to 6 havo and vwo (general high and pre-academic education).

Specialized categories refer to education for pupils with learning difficulties. Quality in education is generally difficult to measure. In order to take the quality of education into account, moves to higher grades and examination results are included (success rates). As outputs of the educational process, we therefore use the number of pupils multiplied by these success rates.

Resources

The resources used can be divided into five categories or classes of costs:

• Executive board and management;

• Administrative personnel;

• Teaching personnel;

• Property operation (excluding rent);

• Material supplies.

Since local governments are responsible for providing school buildings, we exclude capital cost.

Resource prices

The relative prices of the staff categories are distinguished by region and year. Averaging personnel costs per full-time equivalent over regions and years by a regression analysis, provides a labour price for each staff category for each region in a certain year.

The prices for property operation and materials are assumed to be the same for all educational institutions, and thus only vary over the years. Since property operation costs are building-related costs, such as energy and cleaning, the energy price indices of Statistics Netherlands are used for property operation. For the material costs, the national consumer price index of Statistics Netherlands is used.

Managerial variables

As characteristics of cost efficiency, we include variables that are fully exogenous or can be regarded as management instruments. Therefore the following indicators are used:

• Schools per institution;

• Sites per institution;

• Average school size;

• Average site size;

• Herfindahl index;

• Average education time;

• Average group size;

• Share of education time >1000 hours;

• Vintage buildings (years).

Note that a school board operates one or more schools. So the average school size refers to the size of the schools that are supervised by the same school board. The size of these schools can vary substantially. In order to bring this into the picture, we use a concentration measure reflected by the Herfindahl index (Herfindahl, 1950). A low Herfindahl index indicates many small institutions, a high index a few dominant large institutions. If there is only one school under a board, the Herfindahl index equals 1.

Data resources, data checks and manipulations

We use different databases for the analyses. The number of pupils is taken from the public files of the Office of Education (DUO) of the Ministry of Education, Culture and Science (OCW). The numbers on education returns are supplied by the Education Inspectorate. The financial data and the data on teaching time come from the database of Windows for Accountability. The staff numbers and salary data are also provided by DUO. Finally, the price development of energy and consumer goods and services, as well as the urbanization of the municipalities, are collected by Statistics Netherlands. The years for which all necessary data are available are 2007–10.

We applied a number of checks on these data. A statistical description of the data is given in Table 1. As explained earlier, note that the prices on property operation and material supplies only vary over the years and not over school boards. Furthermore, we deleted all observations with missing data on one or more of the relevant variables. Institutions that own school buildings are excluded from the data set due a complete different cost structure. Finally, a data set remained with 265 observations over the period 2007–2010. Due to this selection, small institutions are underrepresented.

Table 1. Statistical description data, 2007–2010 (N = 265)

Variable	Mean	Standard deviation	Minimum	Maximum
Production
Pupils, grades 1 + 2	2318.5	3882.5	232.0	26,204.3
Pupils, vocational	1051.9	1779.9	0.0	13,625.2
Pupils, general high+pre-academic	1755.0	3077.4	0.0	24,477.7
Educational return, grades 1 + 2	102.7	4.7	87.7	115.9
Educational return, vocational	90.1	3.5	73.3	98.8
Educational return, general high/pre-academic	66.9	7.2	48.3	87.2
Costs
Board/management	2,038,185.9	4,069,952.3	0.0	32,748,198.0
Administrative personnel	3,451,950.9	6,150,231.0	0.0	56,175,556.0
Teaching personnel	25,083,974.6	42,244,083.8	2,266,426.5	343,008,256.0
Property operation	2,358,974.7	3,410,908.0	26,190.0	28,095,000.0
Material supplies	5,572,316.8	8,711,928.2	575,828.0	77,556,000.0
Prices
Price of board/management	101,793.9	3516.6	95,475.0	110,339.0
Price of administrative personnel	47,741.8	2724.0	39,904.0	52,967.0
Price of teaching personnel	66,644.5	3081.1	59,948.0	74,661.0
Price of property operation	370.1	14.8	342.0	380.5
Price of material supplies	105.3	0.8	104.1	106.7
Explanatory variables
Schools per institution	3.0	4.6	1.0	34.0
Sites per institution	6.4	10.2	1.0	74.0
Average school size (pupils)	1950.1	1025.6	330.1	8562.6
Average site size (pupils)	931.7	444.2	277.0	2987.2
Herfindahl index	0.8	0.3	0.0	1.0
Average group size (pupils)	22.1	5.2	13.6	49.6
Average education time (hours)	983.2	53.8	858.4	1269.3
Share of education time >1000 hours	0.6	0.2	0.0	1.0
Vintage buildings (years)	34.6	15.7	0.0	89.0

The average secondary school in the Netherlands had 2,300 pupils in the first two grades (also including practical education, primary education, or senior vocational education), more than 1,000 pupils in junior vocational education (vmbo) and less tha 1,800 in senior general secondary education (havo) or pre-university education (vwo). We also see that there is some variation in educational return. The costs can be divided across five categories:

• management (5%);

• administrative staff (9%);

• teaching staff (65%);

• property operation (6%);

• material supplies (15%).

There is a large variation in the scale of the educational institutions. Note that we distinguish different scale levels: institutional (or board) level, school level (educational entity) and geographical site level. The smallest institution consists of one school, the biggest one runs 34 schools. The smallest average school size within an institution is 330 pupils, the biggest is about 8,500 pupils. Average scale on a site level is about 930 pupils, whereas the smallest site level scale equals about 280 pupils and the largest site level scale about 3,000 pupils.

IV. Estimation and results

The model is specified as a translog cost function and corresponding cost share equations, which are derived from the cost function. The translog function is a second order Taylor approximation. The specification of the model includes three output variables (with a correction for quality in terms of educational returns), five input price variables and a time trend to measure technical change. The reason these variables were chosen was discussed in the previous section.

Since we are dealing with a relatively large number of cross-sectional units and a limited number of periods, we ignore the fact that we are dealing with panel data (with respect to intra-firm correlations). Not much harm is done here, since the between variance is far more relevant for the estimation than the within variance. For that reason the standard errors may have a little downward bias. We pool all the data in one dataset and control for the time varying effects by including a time trend variable.

Homogeneity of degree one in prices and symmetry are imposed by adding restrictions to the model. Aside from these imposed theoretical requirements, a few other requirements also need to be fulfilled, such as monotonicity and concavity in input prices (Färe & Primont, 1995). These requirements can be tested posteriorly. An estimated cost function is monotonic in input prices if the fitted cost shares are positive. Concavity can be tested by exploring necessary and sufficient conditions for concavity.

As mentioned before the model is estimated by the method of non-linear least squares.

Results

Several model specifications were used, in particular with respect to the managerial variables. Most of them show no effect at all on the cost structure. In the final model presented here, only group size, squared group size, education time, the average age of capital, and resource prices seem to be relevant. The estimates are summarized in Table 2.

Table 2. Estimates of cost function

Term	Parameter	Estimate	Standard Error	t-stat.
grades 1-2	b1	0.694	0.038	18.224
vocational	b2	0.165	0.025	6.529
general	b3	0.145	0.026	5.678
grades 1–2 * grades 1-2	b11	−0.187	0.060	−3.112
grades 1–2 * vocational	b12	0.110	0.031	3.583
grades 1–2 * general	b13	0.096	0.032	2.988
vocational * vocational	b22	0.011	0.010	1.017
vocational * general	b23	−0.111	0.024	−4.595
general * general	b33	0.012	0.013	0.888
price management	c1	0.055	0.015	3.658
price adm. personnel	c2	0.083	0.020	4.163
price teachers	c3	0.591	0.023	25.363
price energy	c4	0.103	0.016	6.412
price materials	c5	0.168	0.015	11.113
price management * price management	c11	0.083	0.084	0.985
price management *price adm. personnel	c12	−0.067	0.043	−1.547
price management * price teachers	c13	0.040	0.067	0.599
price management *price energy	c14	0.009	0.036	0.247
price management * price materials	c15	−0.065	0.054	−1.192
price adm. personnel * price adm. personnel	c22	−0.140	0.066	−2.127
price adm. personnel * price teachers	c23	0.016	0.060	0.262
price adm. personnel * price energy	c24	0.060	0.037	1.598
price adm. personnel * price materials	c25	0.132	0.044	3.025
price teachers * price teachers	c33	−0.080	0.098	−0.817
price teachers * price energy	c34	−0.011	0.047	−0.244
price teachers * price materials	c35	0.036	0.057	0.624
price energy * price energy	c44	−0.074	0.041	−1.802
price energy * price materials	c45	0.017	0.037	0.454
price materials * price materials	c55	−0.120	0.064	−1.860
grades 1–2 * price management	e11	0.003	0.003	1.112
grades 1–2 * price adm. personnel	e12	0.002	0.005	0.497
grades 1–2 * price teachers	e13	−0.003	0.006	−0.453
grades 1–2 * price energy	e14	−0.001	0.003	−0.274
grades 1–2 * price materials	e15	−0.002	0.003	−0.629
vocational * price management	e21	0.000	0.001	−0.149
vocational * price adm. personnel	e22	0.003	0.002	1.998
vocational * price teachers	e23	−0.004	0.002	−2.106
vocational * price energy	e24	0.001	0.001	0.723
vocational * price materials	e25	0.000	0.001	0.355
general * price management	e31	−0.003	0.002	−1.953
general * price adm. personnel	e32	−0.010	0.003	−3.711
general * price teachers	e33	0.016	0.004	4.432
general * price energy	e34	−0.003	0.002	−1.520
general * price materials	e35	0.001	0.002	0.610
Trend	h1	−0.022	0.005	−4.402
trend * price management	j11	0.000	0.004	0.022
trend * price adm. personnel	j12	0.007	0.005	1.346
trend * price teachers	j13	0.009	0.006	1.471
trend * price energy	j14	−0.010	0.004	−2.321
trend * price materials	j15	−0.007	0.004	−1.663
ineff. due to price management	δw1	−0.097	0.033	−2.982
ineff. due to price adm. personnel	δw2	−0.549	0.112	−4.915
ineff. due to price teachers	δw3	0.618	0.134	4.599
ineff. due to price energy	δw4	−0.043	0.035	−1.212
ineff. due to price materials	δw5	0.071	0.033	2.191
inefficiency constant	δz0	−15.106	3.635	−4.156
ineff. due to group size	δz1	1.051	0.375	2.801
ineff. due to group size^2	δz2	−0.038	0.011	−3.465
ineff. due to education time	δz3	0.006	0.001	6.154
ineff. due to age capital	δz4	0.005	0.003	1.873

Reliability of estimates

Table 2 shows that in a statistical sense, the cost function model fits the data rather well. The results derived from this cost function are plausible. The cost equation has a high explanatory variance. The majority of the estimated parameters are significant at the 5% level. Most R²’s of the share equations are in line with previous results (Haelermans 2012; Haelermans, De Witte, and Blank 2012). The requirements regarding monotonicity and concavity are also fulfilled for almost all observations. The monotonicity property tells us that input demand is always positive, which is the case for all observations and in particular for the average institution for all resources. A necessary condition for concavity is the negativity of the own elasticities of substitution. This condition also holds for the average institution and is valid for all the observations for all resources, except for management. It shows that management does not respond to the expected economic rationale. Finally, the condition of negative semi-definite of the matrix of elasticities of substitution only holds for a minority (9%) of the observations. However, this is a sufficient rather than a necessary condition, and since we already observed that the management resource shows some economic irrationality, it was expected that this condition would not hold.

We also tested the significance of each equation in the system separately by imposing the restriction that all the parameters (except the constant) equal zero. Based on likelihood ratio tests, all the null hypotheses were rejected.

Cost efficiency

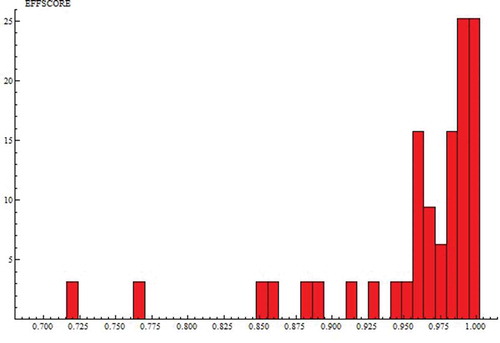
Equation (9)(9) $\widehat{CE}=exp\left[-h\left(z,w,\hat{\delta }\right)\right]$(9) can be applied to determine the cost efficiency of each educational institution. Figure 1 shows the distribution of the efficiency scores in 2010.

Figure 1. Distribution of cost efficiency scores, 2010

The average cost efficiency is 96%. This means that by increasing the efficiency, on average 4% of the costs could be saved without reducing the number of pupils or the quality of the education. The efficiency scores vary between 72% and 100%.

Explaining factors in cost efficiency

Table 3 shows the cost elasticities with respect to the various determinants, represented by the median, the first quartile, and the third quartile. It shows that the elasticity with respect to group size (the combined effect of the single and quadratic term) equals almost −27%, indicating that a 10% increase in group size – say from 20 to 22 pupils – decreases costs by almost 3% (=−27%*10%). A 10% increase in education time leads to a 1.2% increase in costs. Older vintages of capital also increase costs. For education time and age of capital, quadratic terms were also included but they did not improve the fit of the model.

Table 3. Cost elasticities of cost efficiency determinants

Property	Median	Q1	Q3
Group size	0.446	0.141	0.952
Group size^2	−0.702	−1.411	−0.244
Education time	0.121	0.036	0.279
Age capital	0.002	0.001	0.008
[Group size + group size^2]	−0.272	−0.452	−0.103
Price of management	−0.002	−0.004	−0.001
Price of administrative personnel	−0.011	−0.025	−0.003
Price of teachers	0.012	0.003	0.028
Price of energy	−0.001	−0.002	0.000
Price of materials	0.001	0.000	0.003

The elasticities with respect to resource price reflect the direct effect on the cost shares. From this, we conclude that management, administrative personnel, and energy are being underutilized, whereas teachers and material supplies are being over-utilized. From the calculated elasticities, it is obvious that the extent of over- or underutilization is limited. Only in the case of administrative personnel and teachers there seems to be a misallocation of a little more than 1%.

The effects on cost efficiency of the concentration of students, the seniority of staff, the average school size, the average site size, the number of sites, and the teacher absenteeism are negligible. Estimates were highly unreliable and, in most cases, extremely small.

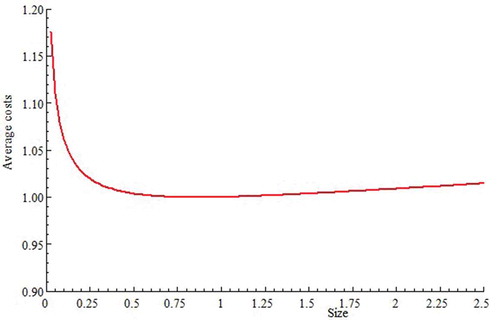
Scale effects

Scale effects refer to the relation between the size of an institution and the costs per unit of a product or service. Economies of scale arise when the costs per unit decrease as the institutional size increases. Diseconomies of scale occur when the costs per unit increase as institutional size increases. Figure 2 shows that the graph of the costs per unit is more or less L-shaped. The institution size, given by an index, is shown on the horizontal axis. An index of 1 refers to an institution of average size. An index of 2 refers to an institution twice the size of the average institution. The costs per unit (combination of number of pupils and performance) are shown on the vertical axis. This variable is also given in an index. An index of value 1 gives the costs per unit for the average institution. Small institutions have high costs per unit. These drop rapidly as the size of the institution increases. Institutions of 0.8 to 1 times the average size, have the lowest average costs. For a larger scale, costs per unit slowly increase once more.

Figure 2. Costs per unit as a function of institutional size

Although the optimum size may differ between studies, this L-shape is common in research (Bee and Dolton 1985; Foreman-Peck and Foreman-Peck 2006; Smet and Nonneman 1998; Watt 1980).

Technical change

Technical change is deduced from the change in costs over time, correcting for changes in the production, input prices, and operational management of individual institutions. Therefore, this is purely productivity growth (lower costs) resulting from technological, institutional, or social changes.

The annual technical change – the h₁-parameter in Table 2 with opposite sign- is, on average, 2.2%. This indicates that between 2007 and 2010, schools improved their productivity substantially. Technical change is input biased, since the optimal allocation of resources shifts through time. The usage of labour intensifies at the expense of the usage of energy and materials. The parameters of the various types of labour j₁₁, j₁₂ and j₁₃ are all positive, whereas the corresponding parameters of energy and material supplies j₁₄ and j₁₅ are negative.

V. Conclusions

This article discusses a rather uncommon variant of stochastic frontier analysis. Using the scaling property, the influence of exogenous variables on efficiency can be modelled and estimated in one stage. This approach also opens the possibility of estimating a system of equations, including the cost function and the corresponding cost share equations. By including resource prices in the efficiency component in the cost function, the allocative component is also brought into the cost share equations, avoiding complex alternatives based on shadow cost pricing.

The model’s application to the Dutch education sector shows that it provides reliable and plausible estimates. It also shows that increasing the average group size may lead to a reduction in costs. Schools can therefore decide to reduce the number of classes. This type of upscaling will, of course, have a ceiling, which could not be established empirically. Schools probably avoid this upscaling to the limit because of the perceived negative quality consequences. The same holds for the education time. School boards may save money by decreasing education time, which is also not a popular measure. Money can also be saved by renewing of renovating school buildings. In general school boards cannot be accounted for the high costs of aged buildings, since this is a matter of local government. Further, the school board will only have limited possibilities to reduce costs by reallocating between different types of resources. It seems that most school boards have already exhausted this possibility. For the other managerial variables, no significant effects were found.

Disclosure statement

No potential conflict of interest was reported by the author.