Practical tracking control for stochastic nonlinear systems with polynomial function growth conditions

Abstract

This paper mainly focuses on an output feedback practical tracking controller design for a class of stochastic nonlinear systems with polynomial function growth conditions. Mostly, there are some studies on an output feedback tracking control problem for general nonlinear systems with polynomial function growth conditions in existing achievements. Moreover, we extend it to stochastic nonlinear systems and construct an output feedback practical tracking controller based on dynamic and static phase combined, ensuring that all the states of the stochastic nonlinear system are bounded and the system tracking error can be made arbitrarily small after some large enough time. Finally, a simulation example is provided to illustrate the efficiency of the theoretical results.

KEYWORDS:

• Output feedback practical tracking control
• polynomial function growth conditions
• feedback control with dynamic and static phase
• stochastic nonlinear systems
• states boundness
• output convergence

1. Introduction

For a nonlinear control theory, it is necessary to realize the stabilization of the closed-loop control system [1–5]; on the other hand, the output of a controlled object can also need to track the reference trajectory signal such that it can achieve output tracking control. As one of the current research hotspots, output tracking control has a wide range of applications in practical systems, such as attitude control of spacecraft, military radar tracking control, precise guidance control and industrial robot control [6–8]. In Ref. [4], a robust attitude stabilization controller is proposed consisting of a nominal state-feedback controller and a robust compensator. In Ref. [8], a robust cascade controller including an attitude controller and a position controller is proposed based on the hierarchical control scheme and the robust compensating technique. Furthermore, based on the needs of practical applications, output feedback tracking control for complex nonlinear systems has produced more results in the theoretical field [9–16]. According to the existing papers, control theory research has mainly focused on two kinds of output feedback tracking controls for a series of studies: the first category is asymptotic output feedback tracking control and this applies to the object system which states that information and reference tracking trajectory information are sufficient [17,18] and the second category is the practical output feedback tracking control problem. For many practical systems and their controller design, it is difficult to obtain sufficient information and some of system states and the reference trajectory are not measurable, in this case, it needs to use practical output feedback tracking control to achieve a tracking objective.

Early research on the output feedback controller design is relatively simple for nonlinear systems whose states and output are measurable [14]. When system states are partially unmeasurable or completely unmeasurable, the restriction assumptions of nonlinear term growth conditions are required for unmeasurable states. In Ref. [15], authors have studied the problem of output feedback practical tracking control for a nonlinear system for which the nonlinear term growth condition is a form of the product of a constant and output polynomial function. In Ref. [19], some constraints of the reference trajectory signal in Ref. [15] are eliminated, and output feedback practical tracking control is realized for nonlinear systems that growth conditions depend on high-order unmeasurable states and simultaneously, high-gain observer has been introduced in the output tracking controller design process. In the above description of the reference trajectory, the upper bound of the reference signal and its first derivative has been set; moreover, when the upper bound of the reference trajectory signal and its first derivative is unknown, Zhai and Fei [16] use an increasing power integral method to study the global output feedback practical tracking problem for a class of higher-order nonlinear systems.

Research status of the output feedback tracking control for nonlinear systems is reviewed. However, for a practical system, the external interference is inevitable, and a lot of interference is random which creates ubiquitous stochastic nonlinear systems [20–25]. Naturally, it is desirable to extend the output feedback tracking control results for nonlinear systems to stochastic nonlinear systems; nevertheless, there are few studies in this area, and some key issues (such as output tracking control for stochastic nonlinear systems that meet different growth conditions) have not been effectively addressed. Therefore, the research on the output tracking control problem of stochastic nonlinear systems is challenging and practical.

The paper mainly studies the output feedback tracking control problem for a class of stochastic nonlinear systems which the nonlinear term satisfies the output polynomial function such that the output feedback practical tracking controller based on dynamic and static phase is constructed to ensure that system tracking error converges to the small neighbourhood of zero.

This paper is organized as follows: Section 2 gives the description of the stochastic nonlinear system and the problem to be solved. Section 3 gives the design process and results of the output feedback practical tracking controller, which mainly includes states observer design and boundedness analysis of system states and observer gain. Section 4 gives a simulation example to verify the effectiveness of the output feedback tracking controller. Section 5 summarizes this paper and prospects for future work.

2. Problem description

This paper focuses on the output feedback practical tracking problem for a class of stochastic nonlinear system: (1) $\begin{array}{rl}\text{d}{\eta }_i& ={\eta }_{i+1}\text{d}t+{\varphi }_i(t,u,\eta )\text{d}\omega (i=1,\dots ,n-1)\\ \text{d}{\eta }_n& =u\text{d}t+{\varphi }_n(t,u,\eta )\text{d}\omega \\ y& ={\eta }_1-y_r(t)\end{array}$(1) where $\eta =({\eta }_1,\dots ,{\eta }_n{)}^T\in R^n$, $u\in R$, and $y\in R$ are the states, input and output of the system, respectively; $y_r$ is a given unmeasurable output trajectory and $x_1,\dots ,x_n$ are also unmeasurable states; $\omega$ is an m-dimensional standard Wiener process defined on the complete probability space $(\mathrm{\Omega },\mathrm{\Gamma },\mathrm{P})$ with $\mathrm{\Omega }$ being a sample space, $\mathrm{\Gamma }$ being a filtration, and $\mathrm{P}$ being a probability measure; furthermore, the nonlinear term ${\eta }_i:R^{+}\times R\times R^n\to R^m,i=1,\dots ,n$ is continuous for $t$, and locally Lipschitz in $(u,\eta )$.

Here, the stochastic nonlinear system (1) satisfies the following assumptions on the basis of which the output feedback practical tracking control can be achieved.

Assumption 2.1

There exists positive integer $p$ and known positive constant $c_0$ such that the following inequality holds: (2) $\begin{array}{rl}|{\varphi }_i(t,\eta ,u)|& \le c_0(1+{|{\eta }_1|}^p)(|{\eta }_1|+\cdots +|{\eta }_i|)+c_0,\\ i& =1,\dots ,n\end{array}$(2)

Therefore, we can conclude that the stochastic nonlinear system (1) is dominated by an output polynomial function growth rate system.

Assumption 2.2

The reference output trajectory $y_r$ of the stochastic nonlinear system (1) is continuously differentiable and satisfies the following inequality: (3) $max(|y_r|,|{\dot{y}}_r|)\le c_1$(3) where $c_1$ is a known positive constant.

According to the above description of the system, it leads to the objective of this paper: for any constant $\delta >0$, all the states of the stochastic nonlinear system (1) are well defined and bounded. In addition, there exists a finite time $T>0$ such that for any $t>T$, we can obtain (4) $|y(t)|=|{\eta }_1(t)-y_r(t)|\le \delta$(4)

Remark 2.1

It should be noticed that the output feedback tracking control problem for nonlinear systems with parametric uncertainties and unknown control directions has been mainly studied in Refs. [9–16]. However, by the introduction of stochastic factors, the output feedback tracking control problem for the stochastic nonlinear system is first studied in this paper. Simultaneously, by Assumption 2.1, it can be observed that the nonlinear term of system (1) is dependent on unmeasurable states. Moreover, from Assumption 2.2, it can easily conclude that the reference trajectory $y_r$ has only obtained its upper bound and the upper bound of derivative, which means that it does not need to give a specific description function for the reference trajectory $y_r$ or give it more information. Due to the lack of system states and tracking signal information as well as the system instability caused by the introduction of stochastic factors, this leads to a general tracking control method, such as an asymptotic tracking control method which can no longer solve the output feedback control problem in this paper. For this challenging problem, the paper will focus on the stochastic nonlinear system under Assumptions 2.1 and 2.2, and then construct an output feedback practical tracking controller based on dynamic and static phase such that the output of system (1) can be gradually converged to zero.

3. Practical tracking control

3.1. Time-varying observer design

Above all, according to the description of the stochastic nonlinear system (1) and Assumptions 2.1 and 2.2, we can obtain (5) $\begin{array}{rl}|{\varphi }_i(t,\eta ,u)|& \le c_0(1+{|y+y_r|}^p)(|{\eta }_1|+\cdots +|{\eta }_i|)+c_0\\ & \le c(1+{|y|}^p)(|{\eta }_1|+\cdots +|{\eta }_i|)+c\\ i& =1,\dots ,n\end{array}$(5) where $c$ is a known constant and $c=c_{0}max(1+2^{p-1}{c}_1^p,2^{p-1})$.

For the sake of convenience of calculation and formula derivation, the following simple states transformation is introduced: (6) $\begin{array}{rl}{z}_1& ={\eta }_1-y_r\\ z_i& ={\eta }_i(i=2,\dots ,n)\end{array}$(6) and then, we can obtain the updated stochastic nonlinear system (7) $\begin{array}{rl}\text{d}{z}_i& =z_{i+1}\text{d}t+f_i(t,u,z)\text{d}\omega \\ \text{d}{z}_n& =u\text{d}t+f_n(t,u,z)\text{d}\omega \\ y& =z_1\end{array}$(7) where (8) $\begin{array}{rl}{f}_1(t,u,z)& ={\varphi }_1(t,u,z_1+y_r,z_2,\dots ,z_n)-\frac{\text{d}{y}_r}{\text{d}\omega }\\ f_i(t,u,z)& ={\varphi }_i(t,u,z_1+y_r,z_2,\dots ,z_n)(i=2,\dots ,n)\end{array}$(8) Due to unmeasurable states characteristics of system (7), states observer of system (7) is established (9) $\begin{array}{rl}{\dot{\hat{z}}}_i& ={\hat{z}}_{i+1}+K^i{h}_i(z_1-{\hat{z}}_1)(i=1,\dots ,n-1)\\ {\dot{\hat{z}}}_n& =u+K^n{h}_n(z_1-{\hat{z}}_1)\end{array}$(9) where $h_i>0(i=1,\dots ,n)$ is the coefficient of the Hurwitz polynomial with $s^n+h_1{s}^{n-1}+\cdots +h_{n-1}s+h_n$. $K=AB(t)$ is a high-order gain term which consists of a constant $A$ and a variable $B(t)$ as follows: (10) $\begin{array}{rl}\dot{B}& =-{\alpha }_1{B}^2+{\alpha }_2(1+{|y|}^p{)}^{2}B\\ B(0)& =1\end{array}$(10) Define the system error states as $e_i=z_i-{\hat{z}}_i(i=1,\dots ,n)$, and then, by (1), (7) and (9), the error system can be obtained (11) $\begin{array}{rl}\text{d}{e}_i& =e_{i+1}dt-K^i{h}_i{e}_1\text{d}t+f_i(t,u,z)\text{d}\omega \\ \text{d}{e}_n& =-K^n{h}_n{e}_1\text{d}t+f_n(t,u,z)\text{d}\omega \end{array}$(11)

In order to facilitate the output feedback practical tracking controller design, the transformation of estimated states ${\hat{z}}_i$ and error states $e_i$ is introduced (12) $\begin{array}{rl}{\epsilon }_i& =\frac{e_i}{K^{b+i-1}}(i=1,\dots ,n)\\ {\tau }_i& =\frac{{\hat{z}}_i}{K^{b+i-1}}(i=1,\dots ,n)\end{array}$(12) where $\epsilon =({\epsilon }_1,\dots ,{\epsilon }_n{)}^T,\tau =({\tau }_1,\dots ,{\tau }_n{)}^T,h=(h_1,\dots ,h_n{)}^T$ and $0\le b\le \frac{1}{4p}$ are known constants. Furthermore, by (12), stochastic nonlinear systems (7) and (9) can be converted into (13) $\begin{array}{rl}\text{d}\epsilon & =KH\epsilon \text{d}t-\frac{\dot{K}}{K}{C}_b\epsilon \text{d}t+G(z,K)\text{d}\omega \\ \dot{\tau }& =K{H}_b\tau +Kh{\epsilon }_1-\frac{\dot{K}}{K}{C}_b\tau \end{array}$(13) where (14) $\begin{array}{rl}H& =\left(\begin{array}{cccc}-h_1& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ -h_{n-1}& 0& \cdots & 1\\ -h_n& 0& \cdots & 0\end{array}\right),\\ H_b& =\left(\begin{array}{cccc}0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\\ -h_1& -h_2& \cdots & -h_n\end{array}\right)\\ C_b& =\text{diag}(b,b+1,\dots ,b+n-1)\\ G(z,K)& ={\left(\frac{f_1}{K^b},\frac{f_2}{K^{b+1}},\dots ,\frac{f_n}{K^{b+n-1}}\right)}^T\end{array}$(14)

3.2. Boundedness analysis of system states and gain

Since the closed-loop stochastic nonlinear system (13) satisfies the locally Lipschitz condition on $(\epsilon ,\tau )$, according to Ref. [26], it is concluded that the closed-loop system has a unique solution in interval $[0,t_T)$. Moreover, if $T$ is a maximum value of $t_f$, then $0<T\le \mathrm{\infty }$.

Next, we discuss the bounds of system gain $B(t)$, state $\epsilon$, and $\tau$. First, the appropriate parameters $r_1,r_2,r_3,r_4$ are chosen such that positive definite matrix $P,Q$ and matrix $H,H_b,C_b$ satisfy the following relation: (15) $\begin{array}{rl}& H^{T}P+PH\le -I_n{r}_1{I}_n\le C_{b}P+P{C}_b\le r_2{I}_n\\ & H_b^{T}Q+Q{H}_b^T\le -2I_n{r}_3{I}_n\le C_{b}Q+Q{C}_b\le r_4{I}_n\end{array}$(15) Define the following Lyapunov function: (16) $V(\epsilon ,\tau )={\epsilon }^{T}P\epsilon +{\tau }^{T}Q\tau$(16) and then, we can obtain the trajectory of (16) along with the Ito differentiation for system (13) as follows: (17) $\begin{array}{rl}LV& =-K|\epsilon {|}^2+2{\epsilon }^{T}PG-\frac{\dot{K}}{K}{\epsilon }^T(C_{b}P+P{C}_b)\epsilon \\ & -2K|\tau {|}^2+2K{\tau }^T{\epsilon }_{1}h\\ & -\frac{\dot{K}}{K}{\tau }^T(C_{b}Q+Q{C}_b)\tau +Tr(G^T(P+Q)G)\\ & -\frac{\dot{K}}{K}{\epsilon }^T(C_{b}P+P{C}_b)\epsilon \le r_2{\alpha }_{1}B|\epsilon {|}^2\\ & -r_1{\alpha }_2(1+{|y|}^p{)}^2|\epsilon {|}^2\\ & -\frac{\dot{K}}{K}{\tau }^T(C_{b}Q+Q{C}_b)\tau \le r_4{\alpha }_{1}B|\tau {|}^2\\ & -r_3{\alpha }_2(1+{|y|}^p{)}^2|\tau {|}^2\end{array}$(17) where (18) $\begin{array}{rl}|G|& =({|G_1|}^2+\cdots +{|G_n|}^2{)}^{\frac{1}{2}}\\ & ={\left({\left(\frac{f_1}{K_b}\right)}^2+\cdots +{\left(\frac{f_n}{K^{b+n-1}}\right)}^2\right)}^{\frac{1}{2}}\end{array}$(18) and (19) $\begin{array}{rl}|G_1|& \le c(1+{|y|}^p)((|\epsilon |+|\tau |)+c_1)+c+c_1\\ |G_i|& \le c(1+{|y|}^p)\left(\sqrt{i}(|\epsilon |+|\tau |)+c_1\right)+c+c_1,\\ i& =1,\dots ,n\end{array}$(19) By splitting and enlarging items in (17), we can obtain (20) $\begin{array}{rl}2{\epsilon }^{T}PG& \le 2||P|||\epsilon |(c(1+{|y|}^p)\\ & \times \left(\sqrt{n}(|\epsilon |+|\tau |)+c_1\right)+c+c_1)\\ & \le c||P||(1+c_1)(1+{|y|}^p{)}^2({|\epsilon |}^2+{|\tau |}^2)\\ & +||P||(2nc+c+c_1)|\epsilon {|}^2\\ & +||P||(c{c}_1+c+c_1)\\ & \times 2K{\tau }^T{\epsilon }_{1}h\le K({|h|}^2{|\epsilon |}^2+{|\tau |}^2)\end{array}$(20)

Furthermore, by (17)–(20), the Ito differential equation for system (13) can be organized as (21) $\begin{array}{rl}LV& \le -K|\epsilon {|}^2+c||P||(1+c_1)(1+{|y|}^p{)}^2({|\epsilon |}^2+{|\tau |}^2)\\ & +||P||(2nc+c+c_1)|\epsilon {|}^2+||P||(c{c}_1+c+c_1)\\ & +r_2{\alpha }_{1}B|\epsilon {|}^2-r_1{\alpha }_2(1+{|y|}^p{)}^2|\epsilon {|}^2\\ & -2K|\tau {|}^2+2K{\tau }^T{\epsilon }_{1}h\\ & +r_4{\alpha }_{1}B|\tau {|}^2-r_3{\alpha }_2(1+{|y|}^p{)}^2|\tau {|}^2\\ & +Tr(G^T(P+Q)G)\\ & \le -K|\epsilon {|}^2+c||P||(1+c_1)(1+{|y|}^p{)}^2({|\epsilon |}^2+{|\tau |}^2)\\ & +||P||(2nc+c+c_1)|\epsilon {|}^2+||P||(c{c}_1+c+c_1)\\ & +r_2{\alpha }_{1}B|\epsilon {|}^2\\ & -r_1{\alpha }_2(1+{|y|}^p{)}^2|\epsilon {|}^2-2K|\tau {|}^2\\ & +K({|h|}^2{|\epsilon |}^2+{|\tau |}^2)+r_4{\alpha }_{1}B|\tau {|}^2\\ & -r_3{\alpha }_2(1+{|y|}^p{)}^2|\tau {|}^2+(||P||+||G||)\\ & \times {\left(c(1+{|y|}^p)\left(\sqrt{n}(|\epsilon |+|\tau |)+c_1\right)+c+c_1\right)}^2\end{array}$(21) where the last item in (21) can be magnified as (22) $\begin{array}{rl}& (||P||+||G||)(c(1+|y{|}^p)\\ & \times {\left(\sqrt{n}(|\epsilon |+|\tau |)+c_1\right)+c+c_1)}^2\\ & \le 2(||P||+||G||)(c^2{(1+{|y|}^p)}^2\\ & \times {\left(\sqrt{n}(|\epsilon |+|\tau |)+c_1\right)}^2+{(c+c_1)}^2)\\ & \le 2(||P||+||G||)(2c^2{(1+{|y|}^p)}^2\\ & \times (n{(|\epsilon |+|\tau |)}^2+c_1^2)+{(c+c_1)}^2)\\ & \le 2(||P||+||G||)(2c^2{(1+{|y|}^p)}^2\\ & \times (2n({|\epsilon |}^2+{|\tau |}^2)+c_1^2)+{(c+c_1)}^2)\\ & =(||P||+||G||)\cdot (8n{c}^2{(1+{|y|}^p)}^2({|\epsilon |}^2+{|\tau |}^2)\\ & +4c^2{(1+{|y|}^p)}^2{c}_1^2+2{(c+c_1)}^2)\end{array}$(22)

After simplification, we can obtain (23) $\begin{array}{rl}LV& \le -(K-K{|h|}^2-||P||(2nc+c+c_1)-r_2{\alpha }_{1}B)|\epsilon {|}^2\\ & -(1+{|y|}^p{)}^2(r_1{\alpha }_2-c||P||(1+c_1)\\ & -8n{c}^2(||P||+||Q||))|\epsilon {|}^2\\ & -(K-r_4{\alpha }_{1}B)|\tau {|}^2\\ & -(1+{|y|}^p{)}^2(r_3{\alpha }_2-c||P||(1+c_1)\\ & -8n{c}^2(||P||+||Q||))|\tau {|}^2+||P||(c{c}_1+c+c_1)\\ & +(4c^2{(1+{|y|}^p)}^2{c}_1^2+2{(c+c_1)}^2)(||P||+||Q||)\end{array}$(23) By observation of (23) and offset principle, parameter ${\alpha }_2$ can be chosen as (24) $\begin{array}{rl}{\alpha }_2& \ge \frac{c||P||(1+c_1)-8n{c}^2(||P||+||Q||)}{r_1}\\ {\alpha }_2& \ge \frac{c||P||(1+c_1)-8n{c}^2(||P||+||Q||)}{r_3}\\ {\alpha }_2& \ge {\alpha }_1>0\end{array}$(24)

Since $B\ge 1$, parameter $A$ needs to satisfy the following relationship: (25) $\begin{array}{rl}A& \ge \frac{||P||(2nc+c+c_1)+r_2{\alpha }_1}{1-{|h|}^2}\\ A& \ge r_4{\alpha }_1\\ A& \ge 1\end{array}$(25) According to the above equation for the choice of parameters, (23) can be translated into (26) $\begin{array}{rl}LV& \le -K({|\epsilon |}^2+{|\tau |}^2)+||P||(c{c}_1+c+c_1)\\ & +(4c^2{(1+{|y|}^p)}^2{c}_1^2+2{(c+c_1)}^2)(||P||+||Q||)\\ & \le -\frac{A}{max({\lambda }_{max}(P)+{\lambda }_{max}(Q))}\\ & \cdot V+||P||(c{c}_1+c+c_1)\\ & +(4c^2{(1+{|y|}^p)}^2{c}_1^2+2{(c+c_1)}^2)(||P||+||Q||)\end{array}$(26)

To avoid the lengthy and cumbersome of (26), parameters $E_1\text{and}{E}_2$ are defined as follows: (27) $\begin{array}{rl}{E}_1& =\frac{A}{max({\lambda }_{max}(P)+{\lambda }_{max}(Q))}\\ E_2& =||P||(c{c}_1+c+c_1)\\ & +(4c^2{(1+{|y|}^p)}^2{c}_1^2+2{(c+c_1)}^2)(||P||+||Q||)\end{array}$(27) Since the closed-loop system has a unique solution in interval $[0,\mathrm{\infty })$, by (26) and (27), we can obtain (28) $V(\epsilon (t),\tau (t))\le V(\epsilon (0),\tau (0))e^{-\frac{E_1}{A}t}+\frac{E_2}{E_1},t\in [0,T)$(28) such that states $\epsilon (t)$ and $\tau (t)$ of the stochastic nonlinear system (13) are well defined and bounded on $[0,T)$.

Correspondingly, by $y=z_1=({\epsilon }_1+{\tau }_1)K^b$ and $|y|\le (AB{)}^b(|{\epsilon }_1|+|{\tau }_1|)$, we can obtain $|y|\le (AB{)}^b{E}_3$. According to the boundedness of $\epsilon$ and $\tau$ on $[0,T)$, combined with the above-obtained $|y|\le (AB{)}^b{E}_3$ and $b\in \left(0,\frac{1}{4p}\right)$, we can obtain (29) $\begin{array}{rl}\dot{B}& =-{\alpha }_1{B}^2+{\alpha }_2(1+{|y|}^p{)}^{2}B\\ & \le -{\alpha }_1{B}^2+{\alpha }_2(1+{({(AB)}^b{E}_3)}^p{)}^{2}B\\ & \le -{\alpha }_1{B}^2+2{\alpha }_2(1+{({(AB)}^b{E}_3)}^{2p})B\\ & \le -{\alpha }_1{B}^2+2{\alpha }_{2}B\left(1+{(AB)}^{\frac{1}{2}}{E}_3^{2p}\right)\end{array}$(29) which implies that (30) $B(t)\le \frac{4{\alpha }_2^2{\left(1+E_3^{2p}\sqrt{A}\right)}^2}{{\alpha }_1^2}$(30)

Through the above analysis, we can prove that the system gain $B(t)$ is well defined and bounded on $[0,T)$ with $T=\mathrm{\infty }$.

3.3. Output feedback tracking controller design

According to the boundedness analysis of Section 3.2, this section first gives the theorem of the output feedback practical tracking controller.

Theorem 3.1:

Consider a class of stochastic nonlinear system (1) whose output is $y=x_1-y_r$ under Assumptions 1 and 2. By choosing appropriate parameters $a_i,h_i,A,{\alpha }_1{\alpha }_2$, the following output feedback practical tracking controller can be designed: (31) $u=-(K^n{a}_1{\hat{z}}_1+K^{n-1}{a}_2{\hat{z}}_2+\cdots +K{a}_n{\hat{z}}_n)$(31) where $B$ is defined by (10) and $a_i>0$ is the coefficient of Hurwitz polynomial $s^n+h_1{s}^{n-1}+\cdot \cdot \cdot +h_{n-1}s+h_n$ with $h_i=a_{n-i+1}$. Then, for any $\delta >0$, there exists a finite time $T$ such that $y=|x_1-y_r|\le \delta$ and all the states of stochastic nonlinear systems (1) and (13) are bounded on $[0,T)$ under the action of the output feedback practical tracking controller (31).

The proof process of Theorem 3.1 is given as follows.

Proof:

There exists a time $T=T_1$ such that (32) $\begin{array}{rl}& V(\epsilon (0),\tau (0))e^{-\frac{E_1}{A}t}\le \frac{E_2}{E_1}\\ & t\ge T\end{array}$(32) and hence, (33) $V(\epsilon (t),\tau (t))\le \frac{2E_2}{E_1},t\ge T=T_1$(33) It should be noticed that $E_1$ contains parameter $A$.

According to (26), it can be concluded that (34) ${\lambda }_{min}(P)|\epsilon {|}^2+{\lambda }_{min}(Q)|\tau {|}^2\le V(\epsilon (t),\tau (t))$(34) and then, (35) ${\epsilon }_1^2(t)+{\tau }_1^2(t)\le \frac{E_4}{A}$(35) By using $|y|\le (AB{)}^b{E}_3$ and (33)–(35), we can obtain (36) $\begin{array}{rl}|y|& \le A^b{B}^b(|{\epsilon }_1(t)|+|{\tau }_1(t)|)\\ & \le \sqrt{2({\epsilon }_1^2(t)+{\tau }_1^2(t))}\le \sqrt{\frac{2E_4}{A}}\end{array}$(36) Simultaneously, for any $t\ge T$, there exists (37) $B(t)\le \frac{4{\alpha }_2^2{\left(1+{\left(\frac{2E_4}{A}\right)}^p\sqrt{A}\right)}^2}{{\alpha }_1^2}$(37) and combined with (36), we can further obtain (38) $\begin{array}{rl}{y}^2(t)& =(A^b{B}^b{)}^2(|{\epsilon }_1(t)|+|{\tau }_1(t)|{)}^2\\ & \le 2A^{2b}{B}^{2b}({\epsilon }_1^2(t)+{\tau }_1^2(t))\\ & \le 2\cdot \frac{{16}^b{\alpha }_2^{4b}{E}_4}{{\alpha }_1^{4b}{A}^{1-2b}}\cdot {\left(1+\frac{2^p{E}_4^p}{A^{p-\frac{1}{2}}}\right)}^{2b}\end{array}$(38) Through the above proof and analysis, the output $|y(t)|$ of stochastic nonlinear systems (1) and (13) can be gradually converged to zero by choosing sufficiently large $A$ with $t\ge T$.

The proof of Theorem 3.1 is over such that the output feedback practical tracking controller design for the stochastic nonlinear systems (1) and (13) is achieved.

4. Simulation example

This section considers a class of stochastic nonlinear systems under Assumptions 2.1 and 2 as described below to verify the output feedback tracking controller designed in Section 3: (39) $\begin{array}{rl}\text{d}{\eta }_1& ={\eta }_2\text{d}t+\text{d}\omega \\ \text{d}{\eta }_2& =u\text{d}t+{\eta }_2\ln (1+0.8{\eta }_1^2)\text{d}\omega \\ y& ={\eta }_1-y_r\end{array}$(39) where the corresponding parameter values of the system are set to (40) $c_0=0.78,c_1=0.3,p=2$(40) and $\omega$ is the $m$-dimensional standard Brownian motion defined on the probability space $(\mathrm{\Omega },\mathrm{\Gamma },\mathrm{P})$, where $\mathrm{\Omega }$ is the sample space, $\mathrm{\Gamma }$ is the algebra, and $\mathrm{P}$ is the probability measure.

In the numerical simulation, the tracking trajectory is specifically set to (41) $y_r(t)=0.3\sin t$(41) and the nonlinear terms ${\varphi }_1$ and ${\varphi }_2$ of the stochastic nonlinear system (39) are defined as (42) $\begin{array}{rl}{\varphi }_1& =1\\ {\varphi }_2& ={\eta }_2\ln (1+0.8{\eta }_1^2)\end{array}$(42)

Set (43) $\begin{array}{rl}{z}_1& ={\eta }_1-y_r\\ z_2& ={\eta }_2\end{array}$(43) and ${\hat{z}}_1$ and ${\hat{z}}_2$ are the estimated values of $z_1$ and $z_2$, respectively. Furthermore, the parameters of the output feedback tracking controller are set as follows according to Theorem 3.1: (44) $\begin{array}{rl}h& =(0.5,1{)}^T,a=(1,0.5{)}^T,\\ {\alpha }_1& =0.2,{\alpha }_2=186,\\ A& =785,b=\frac{1}{16}\end{array}$(44)

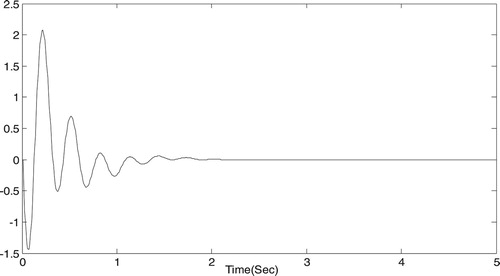
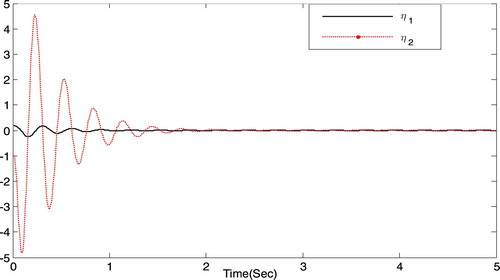
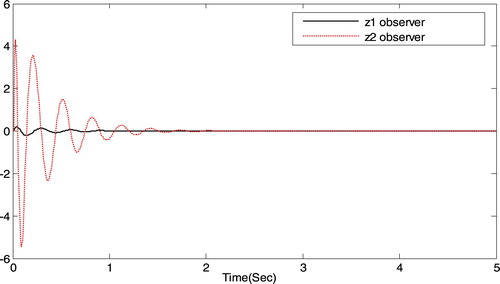
Then, start the system simulation and select the initial value (45) $\begin{array}{rl}{\eta }_1(0)& =0.2,{\eta }_2(0)=-1\\ {\hat{z}}_1(0)& =0,{\hat{z}}_2(0)=0\end{array}$(45) Figures 1–3 show the response characteristics of the closed-loop system (39). By observing the simulation graph, the practical states and the estimated states of the two-dimensional system (39) are bounded and gradually converged. The results verify the effectiveness of the designed output feedback practical tracking controller.

Figure 1. The trajectory of system output $y$.

Figure 2. The trajectory of system states ${\eta }_1$ and ${\eta }_2$.

Figure 3. The trajectory of system observer states ${\hat{z}}_1$ and ${\hat{z}}_2$.

5. Conclusion and future prospects

This paper mainly focuses on the output feedback tracking controller design for a class of stochastic nonlinear systems with polynomial function growth conditions. Mostly, there are some studies on the output feedback tracking control problem for nonlinear systems with polynomial function growth conditions in existing achievements. Moreover, we extend it to stochastic nonlinear systems and construct output feedback practical tracking controller based on dynamic and static phase combined by the Ito stochastic differential theory and selection of appropriate design parameters, ensuring that the system tracking error can be made arbitrarily small after some large enough time. Finally, a simulation example is provided to illustrate the efficiency of the theoretical results.

This paper has made some valuable research results and also produced some further in-depth research of the problem.

In this paper, the control coefficient of the stochastic nonlinear systems which we study is defaulted to $1$, and then, we consider whether it can generalize them to stochastic nonlinear systems with uncertain control coefficients. Consider the following stochastic nonlinear systems: (46) $\begin{array}{rl}\text{d}{\eta }_i& ={\eta }_{i+1}\text{d}t+{\varphi }_i(t,u,\eta )\text{d}\omega (i=1,\dots ,n-1)\\ \text{d}{\eta }_n& =ku\text{d}t+{\varphi }_n(t,u,\eta )\text{d}\omega \\ y& ={\eta }_1-y_r(t)\end{array}$(46) where $k$ is the control coefficient and satisfies (47) $k_1\le |k|\le k_2$(47)

Here, we can observe that the stochastic nonlinear system studied in this paper is a special case ($k=1$) of the system (46). How to design the output feedback practical tracking controller for this type of extended system (46)? It is worth studying on the problem.

Disclosure statement

No potential conflict of interest was reported by the author.

Additional information

Funding

This work was supported in part by the National Natural Science Foundation of China [grant number 61807010] and in part by the Natural Science Foundation of Zhejiang Province of China [grant number LQ18F030007].