Playing with Wigner’s swallow, Baxter’s dog and infinite series

Abstract

A well-known puzzle involving the repeated flying of a swallow between two cyclists is extended to investigate the effect of nonuniform speeds. The resulting generalizations provide examples that can be used in the context of the teaching aspects of the manipulation of infinite series, including the use of telescoping sums and products.

KEYWORDS:

• Recreational mathematics
• kinematics
• infinite series

1. Introduction

In a Mathematical Association of America documentary from 1966 about John von Neumann (1903–1957), the Nobel Prize-winning physicist Eugene Wigner(1902–1995) relates the following story (Nowak & Powell, 1966):

There was a puzzle in the twenties which became rather popular. It dealt with two bicyclists cycling towards each other from the two ends of a forty mile track. A swallow is supposed to fly off from one cyclist towards the other, meet the other cyclist, return to the first one, then go back to the second one and cover shorter and shorter distances. The problem is what is the total distance of the swallow’s flight? The speed of the bicyclists was twenty miles [per hour] and the speed of the swallow is fifty miles per hour.

One can arrive at the solution of the problem rather quickly by noting that the two bicyclists will take just one hour to meet, because they start at opposite ends of a forty mile track and have a speed of twenty miles [per hour] each. During an hour naturally the swallow flies fifty miles, because its [speed is] fifty miles per hour.

Well, few people see the solution of this puzzle and Jonnie didn’t see it either, when Max Born a very well known scientist, a physicist, told him the story. In spite of this, by the time that Born had finished the story Jonnie was ready with the answer. He said, ‘Well fifty miles, of course’. Born astounded and said, ‘You are the first one of my scientist friends who saw the solution at once’. Jonnie said ‘Well, I can’t understand that, it is a simple infinite geometrical series!

And by the time Born finished with the story evidently he had summed up the lengths of the infinitely many distances traversed by the swallow.

Wigner prefaces the story with a comment that it illustrates ‘the unusual speed’ of von Neumann’s thinking. Von Neumann’s ability to perform mental arithmetic ‘at lightning speeds’ was well known (MaCrae, 1992, p. 235) but, as we shall see in the next section, if von Neumann did sum the infinite geometrical series he did so via the well-known formula, rather than by summing ‘up the lengths of the infinitely many distances traversed by the swallow’ in his head.

A variant of the problem is given by the famous English puzzle maker Henry Ernest Dudeney (1967, p. 21) who states it as:

Anderson set off from an hotel at San Remo at nine O’clock and had been walking an hour when Baxter went after him along the same road. Baxter’s dog started at the same time as his master and ran uniformly forwards and backwards between him and Anderson until the two men were together. Anderson’s speed is two, Baxter’s four and the dog’s ten miles an hour. How far had the dog run when Baxter overtook Anderson?

My correspondent in Italy who sends me this is an exact man, and he says, “Neglect the length of the dog and the time spent turning.” I will merely add, neglect also the dog’s name and the day of the month.

In giving the solution to the problem, Dudeney (1967, p. 239) notes that ‘when a friend put this problem before a French professor of mathematics, he exclaimed: ‘Mon Dieu, quelle série!’ quite overlooking the simple manner of solution’.

2. Solving the problem

As Wigner and Dudeney note, this is a very nice problem, which can easily stump the hearer. It certainly left me stumped the first time I heard it many years ago as an undergraduate.

The key to the solution is that the repeated change of direction does not change the fact that the swallow can be assumed to move at a constant speed. Spot that, and you have a good chance of going on to see the quick solution to the problem. Don’t spot that, and you may also be left exclaiming ‘Mon Dieu, quelle série!’.

In what follows, we will consider how Wigner’s version of the problem can be extended.

Let us consider the two cyclists, A and B to initially be separated by a distance $D_0$, each moving towards each other with a speed v and the swallow, S, to be travelling with a speed $u\ge v$. The cyclists will meet in time $\frac{D_0}{2v}$ and the total distance travelled by the swallow will be (1) $D_s=u\frac{D_0}{2v}.$(1) We note in passing that if u = v S travels along with A and meets B at the midpoint after having travelled a distance $\frac{D_0}{2}$.

We can also solve the problem ‘the hard way’ by noting that if after the ith change of direction A and B are $D_i$ apart, then the time between the ith and (i+1)th change of direction is $\frac{D_i}{u+v}$ and in that time S has travelled (2) ${\delta }_{i+1}=\frac{u}{u+v}{D}_i.$(2) Further in that time, the separation between A and B has been reduced by an amount $\frac{2v}{u+v}{D}_i$ and so the separation between A and B at the (i+1)th change of direction of S is (3) $D_{i+1}=\left(\frac{u-v}{u+v}\right)D_i.$(3) Clearly from (3), we can write (4) $D_i={\left(\frac{u-v}{u+v}\right)}^i{D}_0$(4) and from (2) the total distance travelled by S will be (5) $D_S=\sum _{i=1}^{\mathrm{\infty }}{\delta }_i=\frac{u}{u+v}\sum _{i=0}^{\mathrm{\infty }}{D}_i.$(5) Finally, substituting (4) into (5) gives (6) $D_S=\frac{D_{0}u}{u+v}\sum _{i=0}^{\mathrm{\infty }}{\left(\frac{u-v}{u+v}\right)}^i$(6) and recognizing the sum as one of a geometric series with common ratio $\left(\frac{u-v}{u+v}\right)$ leads immediately to the result (1).

This somewhat lumbering formulation and solution of the problem looks almost comical when set beside the simple solution given at the beginning of this section, and in this sense it provides an excellent example of the power of clear thinking. However, formulating the problem in terms of an infinite series does fulfil another role, in that it sets the stage to enable us to think about a more general form of the problem.

3. Generalizing the problem

An obvious generalization of the problem is to let both A, B and S change their speeds at each change of direction of S.

Thus if we let $u_i$ and $v_i$ be the speeds of S and A and B between the ith and (i+1)th change of direction, with $u_i\ge v_i\mathrm{\forall }i$, then we can easily generalize (2) and (3) to (7) ${\delta }_{i+1}=\frac{1}{1+r_i}{D}_i$(7) and (8) $D_{i+1}=\left(\frac{1-r_i}{1+r_i}\right)D_i$(8) where (9) $r_i=\frac{v_i}{u_i}.$(9) Note that while the cyclists’ and swallow’s speeds are both a function of i in (9) it is perhaps, for some readers, more intuitive in what follows to consider the cyclists’ speed to be fixed and the swallow’s speed to change at each change of direction.

We can write (8) as (10) $D_i=D_0\prod _{j=0}^{i-1}\frac{1-r_j}{1+r_j}$(10) and hence the total distance travelled by S will be (11) $D_S=\sum _{i=1}^{\mathrm{\infty }}{\delta }_i=D_0\sum _{i=0}^{\mathrm{\infty }}\left(\frac{1}{1+r_i}\prod _{j=0}^{i-1}\frac{1-r_j}{1+r_j}\right).$(11) Initially, this does not look promising, as the series does not look similar to any an undergraduate is likely to have seen. However, if we think of the problem in terms of using (11) as a basis to try to construct series which we might be familiar with, then results are forthcoming.

In the first instance, let us consider the product term in (11). If this product was to reduce to a factorial term or could be constructed so that it telescoped then we might be able to find a series which we can then sum. It turns out that both of these intuitions are fruitful.

4. Model 1: constructing factorials

First, let’s consider the product term in (11). If we were to pick (12) $\frac{1-r_j}{1+r_j}=\frac{a}{j+1}$(12) then (13) $\prod _{j=0}^{i-1}\frac{1-r_j}{1+r_j}=\frac{a^i}{i!}$(13) which, very helpfully, is the ith term of the Maclaurin expansion for $e^a$.

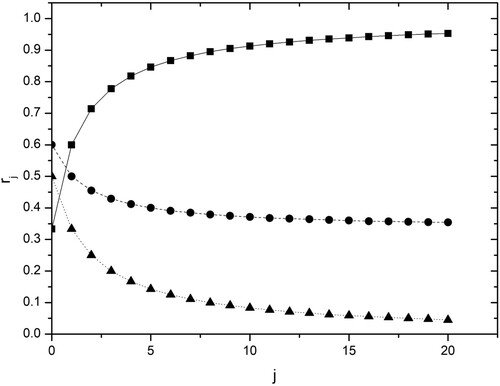
Further, rearranging (12), (14) $r_j=\frac{j+1-a}{j+1+a}$(14) and given $0<r_i=\frac{v_i}{u_i}\le 1$ we thus have the constraint on a that (15) $0\le a<1.$(15) Note that as j increases $r_j$ increases monotonically, approaching unity as j approaches infinity. Given the definition of $r_j$, (9) this means that, for example, if the speed of the cyclists remains constant, the swallow is decreasing in speed at each change of direction (see Figure 1).

Figure 1. Examples of the behaviour of speed ratios $r_j=\frac{v_j}{u_j}$ corresponding to models 1, 2 and 3discussed in the text. Squares: $r_j=\frac{j+1-a}{j+1+a}$; Circles:$r_j=\frac{j+2-a(j+1)}{j+2+a(j+1)}$; Triangles: $r_j=\frac{1}{j+n}$. In the plotted graphs, a=0.5 and n = 2.Note that an increase in $r_j$ corresponds to the swallow slowing down and as $r_j\to 1$ the swallow approaches the speed of the cyclist. If $r_j\to 0$, the swallow’s speed diverges (assuming the speed of the cyclist is nonzero).

Using (13) and (14) in (11) immediately gives (16) $D_S=D_0\sum _{i=0}^{\mathrm{\infty }}\frac{1}{2}\left(\frac{a^i}{i!}+\frac{a^{i+1}}{(i+1)!}\right)=D_0\left(e^a-\frac{1}{2}\right).$(16) For a further generalization of this, see question 2 of the classroom exercises section.

5. Model 2: A telescoping product

Next, consider (17) $\frac{1-r_j}{1+r_j}=a\frac{j+1}{j+2}$(17) This leads to (18) $\prod _{j=0}^{i-1}\frac{1-r_j}{1+r_j}=\frac{a^i}{i+1}$(18) and (19) $r_j=\frac{j+2-a(j+1)}{j+2+a(j+1)}$(19) and given $0<r_i=\frac{v_i}{u_i}\le 1$ we thus have the constraint on a that (20) $0\le a<1.$(20) As j increases $r_j$ decreases monotonically from $r_0=\frac{2-a}{2+a}$, approaching $\frac{1-a}{1+a}$ as j approaches infinity. As noted earlier, given the definition of $r_j$, (9) this means that, if the speed of the cyclists remains constant, the swallow is thus increasing in speed at each change of direction (see Figure 1).

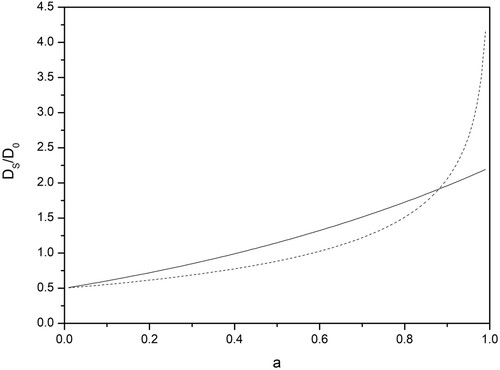
Using (18) and (19) in (11) gives the total distance travelled by the swallow as (21) $D_S=D_0\sum _{i=0}^{\mathrm{\infty }}\frac{1}{2}\left(\frac{a^i}{i+1}+\frac{a^{i+1}}{i+2}\right)=-\frac{D_S}{a}\left(\ln (1-a)+\frac{a}{2}\right).$(21) For a variant of this, see question 3 of the classroom exercises section. Both (16) and (21) are illustrated in Figure 2.

Figure 2. Results for models 1 and 2. Solid line: model 1, Equation (16). Dashed line: model 2, Equation (21). Note that in both cases when a = 0, $r_j=1\mathrm{\forall }j$, or more importantly, $r_0=1$. This means that the swallow and cyclist travel at the same speed and both cyclists and swallow meet having travelled a distance $\frac{D_0}{2}$, with no need for the swallow to change direction. For model 2, the distance travelled diverges as a approaches unity.

6. Model 3: A telescoping sum

Consider a ratio of speeds that is decreasing harmonically in the form (22) $r_j=\frac{1}{j+n}$(22) where n is a positive integer (see Figure 1).

In this case, (23) $\frac{1-r_j}{1+r_j}=\frac{i+n-1}{i+n+1}$(23) and we can show that the product telescopes to give (24) $\prod _{j=0}^{i-1}\frac{1-r_j}{1+r_j}=\frac{n(n-1)}{(i+n-1)(i+n)}$(24) resulting in (25) $D_s=D_0\frac{n(n-1)}{2}\sum _{i=0}^{\mathrm{\infty }}\left(\frac{1}{i+n-1}-\frac{1}{i+n+1}\right)$(25) with this sum telescoping to give the elegant and simple result (26) $D_s=\frac{D_0}{2}(2n-1).$(26)

7. Model 4: A random swallow

Finally, let’s consider a swallow which randomly picks its speed after each change of direction such that $r_i$ is uniformly distributed on [0,1]. The expected value of $D_s$ is given by the integral over the infinite dimensional space of random variables, (27) $E[D_s]=\underset{n\to \mathrm{\infty }}{lim}{D}_0{\int }_0^1\dots {\int }_0^1\sum _{i=0}^n\left(\frac{1}{1+r_i}\prod _{j=0}^{i-1}\frac{1-r_j}{1+r_j}\right)d{r}_0\dots d{r}_n$(27) While this may look complicated it is not, as all the integrals separate and each term in the sum can be evaluated as (28) $\begin{array}{rl}& {\int }_0^1\frac{d{r}_i}{1+r_i}\times {\int }_0^1\left(\frac{1-r_0}{1+r_0}\right)d{r}_0\times {\int }_0^1\left(\frac{1-r_1}{1+r_1}\right)d{r}_1\times \dots \times {\int }_0^1\left(\frac{1-r_{i-1}}{1+r_{i-1}}\right)d{r}_{i-1}\\ & ={\int }_0^1{\frac{dr}{1+r}\times \left[{\int }_0^1\left(\frac{1-r}{1+r}\right)dr\right]}^i.\end{array}$(28) The integrals on the right-hand side of (28) are easily evaluated as (29) $\begin{array}{l}{\int }_0^1\frac{dr}{1+r}=\ln (2)\\ {\int }_0^1\frac{1-r}{1+r}dr=2\ln (2)-1\end{array}$(29) and so (27) becomes (30) $E[D_s]=D_0\ln (2)\sum _{i=0}^{\mathrm{\infty }}{(2\ln (2)-1)}^i.$(30) Once again we have the sum of a geometric progression, giving (31) $E[D_S]=\frac{D_0\ln (2)}{2(1-\ln (2))}.$(31)

7.1. Classroom exercises

Wigner’s swallow and Baxter’s dog are, of course, wonderful puzzles in their own right. But as shown above, they also form a basis for the creation of problems suitable for use with undergraduates in the context of teaching infinite series. These problems give students experience in some of the standard techniques which need to be mastered in the manipulation of series, such as spotting telescoping sums and products, and recasting non-standard series into standard forms by appropriate multiplication or subtraction (as is needed for example to move from the left-hand side to the right-hand side of Equation (21)).

The questions below give examples of how these ideas can be used further in a classroom context.

1. A variation on the original problem is to consider a swallow that travels from A to B with speed $u_A$ and from B to A with speed $u_B$, where $u_A,u_B\ge v$. Show that is such a case the total distance travelled by the swallow is (32) $D_S=\frac{D_0(2u_A{u}_B+v(u_A-u_B))}{2v(u_A+u_B)}.$(32)

2. (a) Following the same steps as are given between Equations (11)–(16) for Model 1, show that if (33) $\frac{1-r_j}{1+r_j}=\frac{a}{j+2}$(33) then (34) $D_s=D_0\left(\frac{1}{a}(e^a-1)-\frac{1}{2}\right)$(34) where $0\le a\le 2$.

   (b) Further, show that if $\frac{1-r_j}{1+r_j}=\frac{a}{j+m}$ where m is a positive integer then (35) $D_S=D_0\left(\frac{(m-1)!}{a^{m-1}}\left(e^a-\sum _{i=0}^{m-2}\frac{a^i}{i!}\right)-\frac{1}{2}\right)$(35) where $0\le a\le m$.

3. Show that if (36) $\frac{1-r_j}{1+r_j}=a\frac{j+1}{j+3}$(36) then (37) $D_s=-2D_0\left(\left(\frac{a-1}{a^2}\right)\ln (1-a)+\frac{2}{a}-\frac{1}{4}\right).$(37)

4. Dudeney notes that the Italian who sent him the problem advised him to ‘neglect … the time spent turning’. Considering the form of the problem where both cyclists are at fixed speed v and the swallow fixed speed u, estimate the number of changes of direction of the swallow if it has a finite, but small, change of direction time $\mathrm{\Delta }t$.

5. Equations (7) and (8) along with $D_S=\sum _{i=1}^{\mathrm{\infty }}{\delta }_i$ provide a simple iteration method which is easily programmed. Write a short programme to allow you to investigate the behaviour of $D_S$ given $r_j=1-exp(-aj)$ where a > 0.

6. The random swallow example given in Model 4 can be generalized so that the swallow picks its speed over the uniform distribution $r_i\in [\alpha ,1]$, where $0\le \alpha \le 1$. Show that in such a case (38) $E[D_s]=\frac{D_0\ln \left(\frac{2}{1+\alpha }\right)}{2(1-\alpha )-2\ln \left(\frac{2}{1+\alpha }\right)}.$(38)

Disclosure statement

No potential conflict of interest was reported by the author.