Two notions of social capital

ABSTRACT

We propose a model that reconciles two aspects of social capital: social capital as reciprocal sharing of favors within a selected group vs. social capital as trust that lubricates transactions in societies. The core assumption is that individuals have productive potentials, e.g., innovations, that can not be put at use autonomously. However, individuals can associate in a club to match productive innovator-implementor dyads among the members. For a given club, allowing one new member has the effect of a) an increased pool of innovations and b) an increased pool of potential implementers. Whether a particular member supports the expansion of the club depends on whether she expects to be an implementor or an innovator. When expansion of membership is decided by vote, both small exclusive clubs and open clubs encompassing the whole society can emerge. The outcome depends both on the voting protocol, on the distribution of innovator and implementer skills, and on the maximal potential club size. Moreover, identical environments may generate multiple equilibrium club sizes. In which of these the society ends up depends on the initial conditions and on the voting protocol.

KEYWORDS:

• Social capital
• matching
• voting in clubs

1. Introduction

The concept of Social Capital is much used across social sciences to explain a wide range of phenomena. With its wide use, the exact definition of social capital varies markedly across disciplines. In particular, the divide appear especially wide between economists and sociologists. The purpose of the present paper is to present a common analytical framework where these two notions of social capital emerge as complementary expressions of the same underlying mechanisms.

Robert Putnam is the scholar who has influenced the most the way economists think about social capital. He defines social capital as “the features of social organization, such as trust, norms, and networks, that can improve the efficiency of society by facilitating coordinated actions.” (Putnam, 1993). The premises of his definition lie in one fundamental question: How is it possible to solve problems of collective actions? Rational behavior often implies cooperation failure as an equilibrium outcome, as in many classic examples from the tragedy of the commons to the prisoner dilemma. However, experimental evidence abounds that agents can successfully manage to cooperate for mutual benefit (Ledyard, 1995). Cooperation requires one fundamental ingredient: trust. Specifically, each agent must trust others to carry on the mutually beneficial action, rather than defecting. High mutual trust is found, not surprisingly, among people with very close connections, such for example, family members. More challenging, however, is the extension of mutual trust beyond the boundaries of the family (or kinship, or clan): “How does personal trust become social trust?” (Putnam, 1993). According to Putnam, associations of any form – what he calls “networks of civic engagement” – are crucial. By participating in groups, individuals enlarge the set of other individuals they can trust. When groups are numerous and interconnected, the set of trustworthy individuals encompasses the whole society. The nature of the groups does not matter (chess clubs, choirs, unions, preaching groups, etc), as long as they connect individuals in stable networks. In turn, these networks facilitate the establishment and enforcement of norms of reciprocity, which ultimately foster trust. The influence of Putnam in economics is apparent from the definition of social capital put forward in the Handbook of Social Economics: “those persistent and shared beliefs and values that help a group overcome the free rider problem in the pursuit of socially valuable activities.” (Guiso et al., 2011), that has received widespread adoption in economics (Casas et al., 2017; Nannicini et al., 2013; Padró Miquel et al., 2015). Putnam’s influence also resonates in one of the most commonly used measure of social capital in the economic literature, the density of associations (Buonanno et al., 2009; Satyanath et al., 2017), that was originally proposed by Putnam himself (Putnam, 1993).

The sociologist Pierre Bordieau is the social scientist credited to have first introduced the term social capital. His notion is quite different from Putnam’s. Bordieau thinks of social capital as “the aggregate of the actual or potential resources which are linked to […] membership in a group which provides each of its members with the backing of the collectivity-owned capital, a ‘credential’ which entitles them to credit, in the various senses of the word.” (Bourdieu, 1986).¹ Clearly group membership is central in his definition as well, but for somewhat different reasons than Putnam’s. Social capital is made of connections, loyalties and privileges. By belonging to a group, individuals can exploit its collective means (of different forms: reputation, information, physical capital) to enhance their trustworthiness (credit), and hence their individual status. Bourdieu is rather vague on the exact mechanism through which bringing different people together in the same group enhances individual payoffs, but he explicitly mentions a “multiplier effect” that increases material and symbolic profits. What he makes very clear, is the exclusive flavor of social capital: the fundamental feature of each group are its limits. High-social capital groups are elite clubs, who allow only affluent members, and manage to exclude others in order to avoid diluting the material value and symbolic prestige of the network: “Through the introduction of new members into a family, a clan, or a club, the whole definition of the group, i.e., its fines, its boundaries, and its identity, is put at stake, exposed to redefinition, alteration, adulteration.” (Bourdieu, 1986). As in Putnam’s definition, the original purpose of the groups does not matter: “The profits which accrue from membership in a group are the basis of the solidarity which makes them possible. This does not mean that they are consciously pursued as such, […].”(Bourdieu, 1986).

A perfect example of Bourdieu’s social capital is provided by the recent empirical work by Haselmann et al. (2018), who analyze members of elite service clubs in Germany, whose official purpose is charity. Membership in this group is a signal of high status, and can be obtained by invitation only. The authors show that bankers who are club members allocate more loans to firms whose CEO belongs to the same club, compared to other firms. Interestingly, they can document that these loans are a form of crony lending, and they do not originate from better information flow within the network of club members.²

How to reconcile Bourdieu’s notion of social capital with Putnam’s one? Both notions build on the possibility for individuals to associate together in groups. However, on one side of the debate Putnam stresses the inclusive nature of groups, who bring different people together. Social capital is a public good, and benefits society as a whole; it is a claim on the individual possessed by the society. The larger the coverage of the club, the better for the members. On the other side, Bourdieu emphasizes the exclusive nature of groups, that split individuals between insiders and outsiders. Social capital is a claim on the social possessed by the individual. Here social capital has the form of favors and privileges, whose value is diluted if more members are allowed into the group.

Hence, a crucial difference between the two approaches is then the scope of the group, and its determinants. In the case of favors, members of a group will want to limit membership by individuals that may compete for favors but without providing other favors in exchange. In the case of trust, all individuals who trust others would like themselves to be trustworthy and also would like others to trust oneself. In order to reconcile, but also contrast, these two notions we establish a framework where there is a trade-off between these concerns. The equilibrium object arising from this trade-off is group size.

We study a model where agents in a population are endowed with one single productive idea – an innovation, and are at the same time (potentially) able to implement other agents’ innovations, but not their own. Agents differ in the productivity of their ideas, and in their implementation capabilities. That agents are excluded from the possibility of implementing their own idea make cooperation crucial. In their capacity as innovator, agents must team up with an implementor to generate surplus. Trust is essential: Entrepreneurs must trust implementors to return back part of the profits. A club assures that the members can trust each other. We assume that within a club, innovations are assigned to the best possible implementer among club members. The surplus of each idea is equally shared between the innovator and implementor. Thus, the club in our model perfectly solves collective action and cooperation problems; members trust each other in the Putnam sense. Again in Putnam’s spirit, efficiency is maximized when the club is inclusive, encompassing the whole society, because then there is optimal matching between ideas and implementers within the club.³

At the same time, our modeling framework allows for the exclusive nature of Bourdieu’s social capital. Club members’ ideas are allocated to the best possible implementer among other club members. When the club is limited in size, the assignment of ideas resembles exchange of favors. Members, and only members, get to implement each others’ ideas. Thus small clubs entail efficiency losses as it is generally the case that a better match for the idea is available among outsiders.

The tension between the two aspects of social capital arises as follows. Innovators would like to have as many implementers as possible in the club, in order to maximize the probability of a good match. For the same reason, innovators would also want to limit the number of entrepreneurs with even better ideas than themselves. Implementors, however, would want to have as many innovators as possible in the club, and as few other implementers as possible, because they compete for the same innovations. It adds to the complexity that each agent, in general, has potential to become both an innovator and an implementor. Which role is more salient for each agent depends on club size: The same agent may oppose expansion when the club is small, but she may want to add more members in a large club.

We consider three different constitutional rules for determining the size of the club. In the first, the club starts out composed only by the agent with the best innovation. He can then invite one new member. The invitation process continues, with members voting by majority rule over inviting new members to join, one new member at a time, or to stop. In the second, the club starts out as the largest possible club, encompassing all agents in society. Then, members vote by majority rule over expelling existing members, starting with the least economically valuable. Third, we consider an autocratic rule in which the economic leader autonomously decides the scope of the club.

Our framework shares some features with La Ferrara (2002) who considers a group that delivers a public good at fixed cost, financed by a tax on the group members. Members of the group get equal access to the good (with some congestion) and pay tax according to income. Similar to us, she is interested in the equilibrium group size, and on how this depends on the heterogeneity of the population. Like in her paper, we consider how different constitutional rules lead to different group sizes.⁴ Contrary to us, she studies individual incentives in group participation, while in our model all agents always want to participate in the club. The mechanism that generates incentives to limit or expand group size is different in the two models. In particular, in our model agents have a rationale for inviting individuals less productive than themselves, whilst in La Ferrara (2002) agents would prefer that only individuals richer than themselves participate. Our model assumes trust and efficient allocation rules within the club. It is silent on how exactly group participation enables individuals to overcome the collective action problem. A complementary work, therefore, is the paper by Tabellini (2008), who provides a microfoundation for cooperation between agents in a large society, sustained by both economic incentives and cultural values.

Two papers that share the spirit of ours are Sabatini (2009) and Antoci et al. (2012). The first article has the elusive concept “social capital” as a starting point but approach it from the empirical side. The second article contains a theoretical growth model and explores how social capital in the Putnam sense develop over time in a growing economy. Our starting point is also theoretical but our economic environment is quite different while our focus is on how social capital may take different forms.

The rest of the paper is structured as follows: in section 2 we explore a simplified model to describe analytically the mechanisms at play; in section 3 we introduce the complete model, which is simulated for different parameters in section 4. Finally, section 5 discusses the results and concludes.

2. The mechanisms: matching versus rent sharing

Before going into the assignment problem in all its details, we start by investigating a stylized set up which allows us to study analytically the mechanisms at play. Compared to the main model, we do some simplifying assumptions: First, all ideas that can be implemented are effectively implemented, and the resulting surplus is shared equally between innovator and implementor. Second, there is a fixed rent $R$ to be shared equally between all the club members. Third, all agents are ex ante identical.⁵

The economy is populated by $n$ identical agents, each endowed with an idea worth $x$. To deliver its surplus $x$, an idea must be implemented. Agents can not implement their own ideas, but can potentially implement other agents’ ideas, as long as they are part of a club. The club is a group of agents of size $m\le n$. Cooperation is always needed to generate any surplus and cooperation is only possible between club members. The probability that agent $i$ can implement the idea of agent $j$ is $p$.

Considering the club as a long-term institution whose members interact repeatedly over several periods, the expected return to each of the $m$ members of the club will be

(1) ${\pi }_i=\frac{R+f(m)x}{m}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}f(m)=m\cdot [1-(1-p{)}^{m-1}].$(1)

Here, the first part of the profit function is the rent component, while the second is the surplus yielded by the productive ideas. Each idea has $(m-1)$ potential implementers. Each agent has a probability $p$ of being able to implement someone else’s idea. Thus $[1-(1-p{)}^{m-1}]$ is the probability that at least one of the $(m-1)$ other members can implement $i$’s idea, and also the fraction of implemented ideas.⁶ The function $f(m)$ can be interpreted as the matching technology, and corresponds to the expected number of implemented ideas. It features increasing returns to scale.⁷

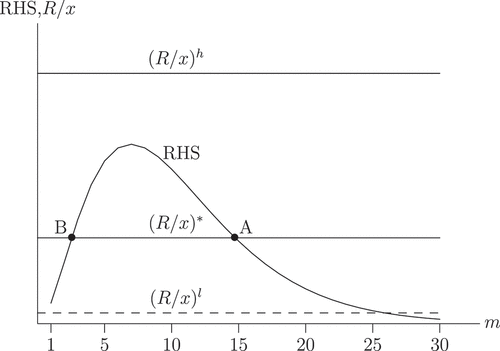
With this return to club members, the club will invite members as long as ${\pi }_i$ increases with $m$

(2) $\frac{\mathrm{\partial }{\pi }_i}{\mathrm{\partial }m}\ge 0\iff x\frac{\mathrm{\partial }f(m)}{\mathrm{\partial }m}\ge {\pi }_i.$(2)

This condition is familiar from the analysis of owner-managed firms: new employees will be hired as long as the contribution from a new employee is larger that the prevailing income to each existing employee (Meade, 1972). In the current setting the contribution from a new club member is the improvement in the matching ideas to implementers. This matching effect is held up against the dilution of rents $R$. By using equations (1)(1) ${\pi }_i=\frac{R+f(m)x}{m}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}f(m)=m\cdot [1-(1-p{)}^{m-1}].$(1) and (2(2) $\frac{\mathrm{\partial }{\pi }_i}{\mathrm{\partial }m}\ge 0\iff x\frac{\mathrm{\partial }f(m)}{\mathrm{\partial }m}\ge {\pi }_i.$(2) ), the condition for expanding the club size is

(3) $R/x\le mf{ }^{\mathrm{\prime }}(m)-f(m)=-(1-p{)}^{m-1}{m}^{2}ln(1-p).$(3)

The left hand side of (3) is the value of the rent relative to the value of one idea. The right hand side is a measure of the increasing return to scale of the matching technology, and it is larger the more convex the $f(\cdot )$ function. In order for an increase in club size to pay off for existing members, the increase in surplus due to the increasing returns to scale has to exceed the effect from dilution of the exogenous rents $R$. The right hand side of (3) is hump-shaped in $m$, starting at $-ln(1-p)$ and asymptotically approaching zero as $m\to \mathrm{\infty }$. It has a maximum for $m=-2/ln(1-p)$.⁸ We plot the right hand side in Figure 1 together with three alternative values of $R/x$, which exemplify three different cases.

Figure 1. First order condition, matching versus rent sharing.

First, if the rent element is low relative to the value of the ideas, $R/x=(R/x{)}^l$, then the right hand side of (3) is larger than $R/x$ and the positive matching effect resulting from new members to the club dominates for moderately sized clubs. The club is expanded until matching is almost certain for all existing club members. In the example, $m=26$ is the club size where the rent dilution effects dominate the matching gain, and further expansion generates a loss for the existing members.

Second, when the rent is large relative to the value of ideas, $R/x=(R/x{)}^h$, the rent dilution effect is strong for all $m$ and too strong for the first member to want to invite another member to the club. In the case of only one member, no productive matching will be realized and the single club member will enjoy $R$ without competition. Furthermore, for any club size $m\ge 2$ the existing members would prefer a smaller club, provided they themselves could remain as member.

Finally, when the rent/idea ratio is at an intermediate level, $R/x=(R/x{)}^{\ast }$, for small $m$ the rent dilution effect dominates and return to club members would decline when $m$ increases (say from 1 to 2 or from 2 to 3). For $m$ higher than $B$, however, the matching effect dominates and expansion of the club increases the return for all club members. The reason for this change in sign is that the value of the matching effect becomes more important as the pool of unmatched members of the club increases. In Figure 1, when $R/x=(R/x{)}^{\ast }$, the club members would benefit from expanding the club all the way until the point $A$. For $m$ to the right of $A$, however, a reduction in club size improves club members’ income. The return function in the intermediate case of $R/x=1$ is plotted in Figure 2.

Figure 2. Return function for intermediate $R/x$.

This intermediate case illustrates one of the core tensions at play also in the main model below: The rent dilution effect gives an incentive to limit the size of the club, i.e. to keep it closed, while the matching effect gives an incentive to increase the size of the club, i.e. to keep it open. The former is social capital as exclusive access to privileges à la Bourdieu, the latter is social capital as efficient networks à la Putnam. At point $A$, these aspects exactly balance. To the right of $A$ the Bourdieu logic dominates and club members would like to see the club size reduced. To the left of $A$ the Putnam logic dominates and club members would like to see the club size increased.

In the rest of the paper, we explore these mechanisms in a richer model, that allows for heterogeneity across agents, and which is disciplined by a more stringent matching process. In this fully fledged model, the rent aspect will appear endogenously, and it will come in the form of exchange of favors. The contribution of new members will depend both on the value of their innovation and on their potential role as innovators.

3. The model

As above, the economy is populated by $n$ agents. Each agent is (potentially) both an innovator and an implementer: in the former capacity, he has a business idea of productivity greater than or equal to zero; in the latter capacity, he may be able to implement other agents’ ideas, either perfectly or mediocrely. When an idea is implemented, it generates a surplus. If the implementer is a perfect match for the idea, the surplus is equal to its productivity. If the implementer is a mediocre match, the surplus is equal to $\beta$ times the productivity of the idea, where $0\le \beta <1$. We typically have in mind values of $\beta$ close to 0. Each agent can implement at most one idea, but he is never able to implement his own idea, not even mediocrely. Hence, cooperation is always needed to generate any surplus.

Formally, $Y$ is the $n\times n$ matrix of implementation capabilities indicators such that: $y_{i,j}=1$ if agent $i$ is perfectly able to implement the idea of agent $j$; $y_{i,j}=\beta$ if agent $i$ is mediocrely able to implement the idea of agent $j$; and $y_{i,i}=0\mathrm{\forall }i$, i.e. the elements on the main diagonal are equal to zero because agents are never able to implement their own ideas. The matrix $Y$ is stochastic: Each element in column $j$ off the diagonal are Bernoulli trials with parameter $p_j$. In other words, for all agents $i\ne j$, $p_j$ is the probability that agent $i$ can implement perfectly $j$’s idea. We denote the vector of all these Bernoulli probabilities $p$. The vector of entrepreneurial ideas of each agent is denoted by the $n-$ vector $x$, where $x_i\ge 0\mathrm{\forall }i$. The production potential of the economy is fully described by the $n\times n$ matrix

(4) $A=Y\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(x),$(4)

where each element $a_{i,j}\ge 0$ is the surplus created if agent $i$ implements agent $j$’s idea.

A club $C$ is a square sub-matrix of $A$ of dimension smaller or equal to $n$, obtained by deleting columns and rows with the same index.⁹ The objective of a club is to efficiently allocate ideas to implementers. The allocation is obtained by selecting the elements of $C$ to yield $\tilde{C}$, so that only one ${\tilde{c}}_{i,j}>0$ remains in each row and each column of $\tilde{C}$. There are several mutually excluding allocations of ideas to implementers, as in general there are overlaps in the implementation capacities, both across implementers for each idea, and across ideas for each implementor. Moreover, these allocations in general generate different total surplus. We work from the assumption that the club chooses the allocation that maximizes average (or total) surplus for the club members. Moreover, we assume that the surplus created by each dyad is shared in equal parts between the implementor and the innovator, leaving nothing for agents outside this dyad.¹⁰ Agent $i$’s profit is, therefore, the sum of his profit as an entrepreneur and his profit as an implementer. The vector of profits is therefore

(5) $\mathbf{\Pi }=1/2(\tilde{C}{\mathbf{1}}_n+{\tilde{C}}^{\mathrm{\prime }}{\mathbf{1}}_n).$(5)

The problem for the club is to assign implementors to ideas, that is to find the $\tilde{C}$ that maximizes the sum of $\mathbf{\Pi }$. This assignment problem is a classic in combinatorial optimization theory, and to obtain the solution we can rely on the Hungarian algorithm developed by Kuhn (1955) and Munkres (1957).¹¹

We think of a club as a long-lasting institution rather than as an ad hoc arrangement. Our assumption reflects the evidence that norms of societal cooperation are very persistent across centuries (Guiso et al., 2016). In particular, the club is initially formed according to the prevailing constitutional rule, and then the production game starts and continues forever. Specifically we assume the following timing:

-1) The following primitives are realized: $x,p,n,\beta$.

0) A club is formed according to the prevailing constitutional rule. The club includes $m\le n$ agents.

1) $Y_1$ is realized, the club allocates optimal ideas to implementors, production takes place and surplus is shared and consumed.

2) Step 1) is repeated for $t=2,\dots ,T$, with $T\to \mathrm{\infty }$.

After stage −1), the profit for each member of each potential club can be calculated in expectation. Expected profits form the basis for the club formation decision.

We consider three constitutional rules that allow agents to associate in groups: elite discretion, invitation, and expulsion, where the two latter involve majority voting among club members.

Under elite discretion, the agent with the most valuable idea decides on whether to invite or exclude club members at own discretion.

Under invitation rule, we assume that an initial club is formed by the agent with the most valuable idea and new members are recruited in sequence according to the value of their idea. The first member decide on whether to invite the second in line. If invited, those two then have a vote over to admit a third member. Majority rule applies, and ties result in invitations. If the third agent is invited to join, a new vote is taken by the three members over inviting the fourth. Votes continue in this fashion until one invitation is rejected by the majority: at that point the current club members remain the permanent configuration of the club.

Under expulsion rule, the initial club includes all agents. First, a vote is taken over permanently expelling the agent with the least productive idea. Majority rules apply, and ties result in keeping the agent. If expulsion is approved, a new vote is taken over the agent which has now the least valuable idea. Votes continue until one expulsion is rejected. At that point, the surviving club members are the permanent configuration of the club.

4. The simulations

In order to analyze the voting equilibriums, we first need to derive the expected profits for each agent under different club configurations. In order to do so, we rely on averaging over repeated simulations.¹² In all the simulations below, we fix the population size to $n=20$. Importantly, we assume that the elements of $x$ are never exactly equal to each other: there are at least some $\epsilon$ differences between agents’ ideas. This implies that we can assume that $x$ is sorted in strictly ascending order. Notice that the constitutional rules under consideration have the property that a club can only be formed among agents sitting in adjacent elements of the ordered vector $x$. This property of our club reflects the evidence that group cooperation is easier among similar individuals, rather than among heterogeneous ones (Alesina & La Ferrara, 2000). Furthermore, this property reduces drastically the possible club configurations that we need to consider when constructing the expected profits, reducing accordingly the computation burden. We focus our attention on different cases that arise from different combinations of $x$ and $p$. Each case represents an archetypal society whose population is characterized by a given economic distribution. In Table 1 we summarize the assumptions and main results in each of the five societies. We also include the resulting conflict of interest that could determine the stable size of the club.

Table 1. Summary of simulation assumptions and results.

		Assumptions regarding distribution of ideas	Results	Conflict of interest
1	Monopoly privileges	One privilege/idea, several potential implementors	Privilege holder wants maximum club size. Implementors want a minimal club with themselves as member.	Between elite and insiders and between insiders and outsiders.
2	Aristocracy privileges	Two privileges/ideas, several potential implementors	As above but idea holders derive profit from also from exclusive access to each other and therefore prefer a limited club size.	Between insiders and outsiders. (Potentially aligned between elite and insiders)
3	Diffuse entrepreneurship	Several ideas with different return potential	As above but with the best ideas taking the role as aristocracy and the weak ideas becoming implementors.	Between insiders and outsiders. (Potentially aligned between elite and insiders).
4	Monopoly and bourgeoisie	One high profit idea and several weaker ideas	As 1 but here the holders of weaker ideas(the bourgeoisie) may prefer a large club if it is sufficiently big.	(Potentially aligned for all.)
5	Aristocracy and bourgeoisie	Two high profit ideas and several weaker ideas	As 2 but here the bourgeoisie may prefer a large club if it is sufficiently big.	Between aristocracy and bourgeoisie.

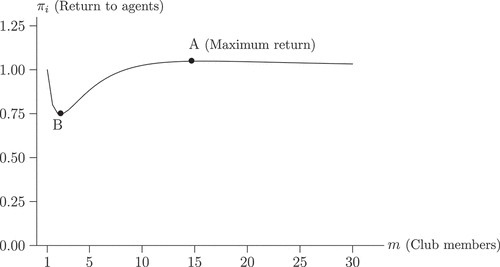
4.1. Society 1: monopoly privileges

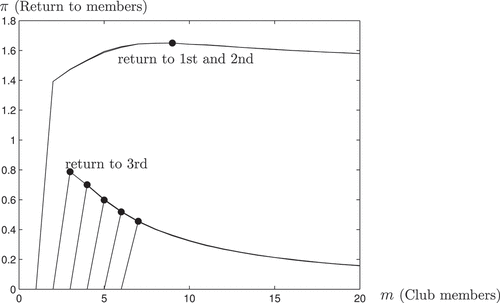
First, we study a society where the production potential of the economy is concentrated in the hands of one single individual. There is only one agent who has (or is handed by a royal privilege) a productive idea, while the others have ideas whose productivity is negligible. In particular, we simulate the scenario with $x_1>0$, and $x_i\approx 0\mathrm{\forall }i\ge 2$.¹³

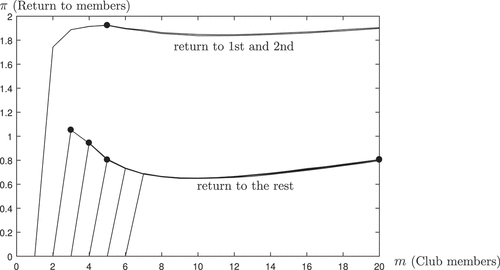
Figure 3 plots the expected profits (denoted with $\pi$) for the first seven agents as a function of club size. The preferred club size for each agent is marked with a dot. The profit of the only agent endowed with a productive idea has an intuitive interpretation: When agent 1 is alone in the club, the surplus is zero because nobody is around to implement his idea. As more agents are included, expected profit for agent 1 strictly increases as the probability that at least one of the other agents is able to implement perfectly (rather than mediocrely) his idea strictly increases. The curve is concave, as the marginal contribution of having one additional implementer is decreasing in group size. In particular, already when the club is formed by thirteen members, the probability of having at least one exact implementer is 0.99. For all the other agents, the expected profits are instead strictly decreasing in group size. Adding more members results only in increased competition for the unique idea available, as only the first agent is endowed with a significant productive idea.

Figure 3. Monopoly privileges.

This simple scenario illustrates one main mechanism at play, namely that agents on the short side of the interaction, the innovator with the idea, want expansion while the ones on the long side, the implementors, want constraints on the expansion of the club (as long as they themselves are members).¹⁴ The societal surplus, however, goes unambiguously up as the size of the club increases. This feature follows by the matching protocol, and is readily seen from the diagram, as the total surplus is twice agent 1’s surplus.

If it is up to the elite to decide (under elite discretion), we get an open club, i.e. $m^D=20=n$. The reason is that the elite is a single agent that has no incentive to limit expansion of the club. The elite agent does not see a subset of the other agents as particularly valuable club mates that she can exchange favors with.

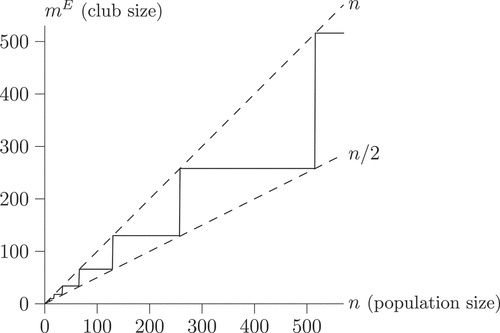
Under invitation rule, however, the process of club expansion stops quite early. Agent 1 is the only in favor of inviting more members, and so she can only get to invite two additional members. When $m=3$ the common interest of agents 2 and 3 blocks any further expansion. Thus the equilibrium club size under invitation rule is $m^I=3.$

Under expulsion rule, the voting equilibrium is slightly more involved. When agents vote over someone’s expulsion, they realize that any expulsion will result in a new vote over the next agent in line; this process may eventually lead to their own expulsion. Solving the voting game by backward induction results in $m^E=18$.¹⁵ The risk of own expulsion is a powerful motive to vote against somebody else’s expulsion in order to stop votes, and consolidate club size. Going beyond this particular example, and extrapolating the profit functions for $n>20$, the exact equilibrium size under expulsion rule depends on $n$. 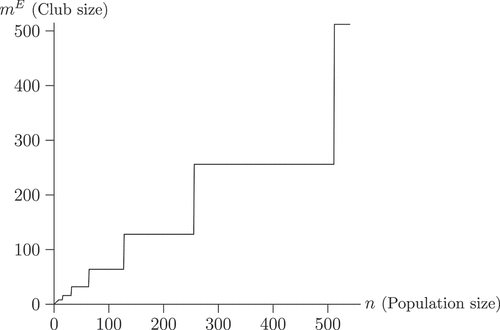This is illustrated in Figure 4 where the stepwise line shows that $m^E$ is sometimes as large as $n$ and never lower than $n/2$.¹⁶ Hence, under this voting protocol, large clubs can be sustained, even though not necessarily encompassing the whole society, but including at least approximately half of the population.

Figure 4. Monopolized privileges: voting equilibria under expulsion rule.

In this society, the distribution of ideas and implementation skills gives an unambiguous conflict of interest: The elite agent wants an open club, while other members want the club to be as small as possible. The resulting club size will crucially depend on the exact constitutional rule: exclusive club under invitation rule, inclusive club under expulsion rule. Hence in this society the economic environment itself can support several club sizes, and the constitutional rule is the key ingredient to resolve the conflict of interest, and arrive at the equilibrium club size.

Here Bourdieu's inspired notion of keeping the club exclusive is the predominant force for most agents. The interest of the fringe is in line with Bourdieu, while only the interest of the elite, who gains from optimal matching, is in line with Putnam. Paradoxically, in this elitist environment, it is only with elite discretion that the club is open, encompassing everyone. Under expulsion rule a quite large and inclusive club could be sustained, however, by fear: Agents keep others in order to preempt an unraveling where they themselves may be next in line to be expelled.

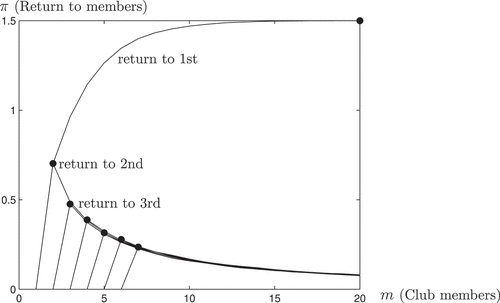
4.2. Society 2: aristocracy privileges

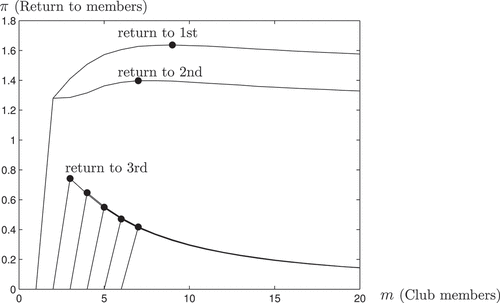
We now move to a society where not only one but a handful of individuals control the privileges and the production capacity of the economy. In particular, we consider an economy similar to the above but where the productive ideas are shared between two agents – the only two members of the aristocracy.¹⁷

Figure 5 plots the expected profits for the first seven agents as a function of club size. In contrast to scenario 1, now the profit function for agent 1 is not strictly increasing, but it has an interior maximum. Agent 2 has an identical profit function. Consider the minimal club including only agents 1 and 2. Their expected profit comes from two sources: from implementing the other agent’s ideas, and from the other agent implementing their own idea. By this exchange of benefits they gain a lot relative to the fringe that is left without any idea to implement. Now if one from the fringe is allowed to enter, the entrepreneurial return to agent 1 and 2 goes up. The reason is that the probability that their idea is implemented exactly goes up. However, agent 1’s share of profit from implementing agent 2’s idea is falling as more members are admitted, due to the increased competition among implementors. The same is true for agent 2 in his role as potential implementor of agent 1’s idea. These two effects work in opposite directions. At first, the increasing entrepreneurial returns more than offset the decreasing implementation returns. Eventually, the marginal gain from increasing the probability of finding a good match does not offset the loss due to increased competition for implementing the other top agent’s idea. Hence, for agents 1 and 2, the optimal club size is between $2$ and $n$, in this case 9. For the fringe composed by all other agents, the expected profits are again falling in group size, as they are only subject to the dilution by competition. In other words, the fringe sees the two ideas as a rent to not dilute, or as favors to share within a exclusive club. It is worth noting that in Society 2, in contrast to Society 1, there is no longer any agent with interests aligned with the social interest.

Figure 5. Aristocracy privileges.

Turning to the analysis of the equilibrium club size under different constitutional rules, a contrast to Society 1 immediately emerges. Under invitation rule, the equilibrium club size is now higher. The productive set of agents counts one more member, so now both agents 1 and 2 favor expansion for small $m$. Their combined votes manage to reach a club of size $m^I=5$ before expansion stops.

Also under expulsion rule the equilibrium club size is different than in Society 1. In particular, it is smaller: $m^E=16$. The intuitive reason is that for large enough clubs, agent 1 and 2 side with their direct neighbors in $x$, and vote in favor of expulsion, because their bliss point is smaller than $n$. However, extrapolating again for $n>20$, the expulsion rule can sustain large clubs as was the case in Society 1.¹⁸ For large $n$, it no longer matters whether the elite is made up of one or of two agents.

The sharpest contrast to Society 1 appears in the case of elite discretion. Here, the exchange-of-favors effect generates an optimal club size of $m^D=9$. In Society 2 the elite, composed here by more than one agent, has an interest in keeping the club smaller.

While Society 1 had the elite subscribing to Putnam and the fringe subscribing to Bourdieu, in Society 2 the elite has some of each. Here the aristocracy wants some of the fringe in the club to increase the likelihood of realizing their own ideas. However, they do not want the club to be too large, as that completely dilutes their own chance of implementing their fellow elite’s idea. Thus it is the mix of the two notions that generates the non-monotonicity in their return schedule. In their optimum, $m=9$, the Putnam’s logic of inclusion exactly balances the Bourdieu’s logic of exclusion.

Society 2 bis: Aristocracy privileges redux A slightly different aristocracy is the one where two members of the aristocracy are endowed with productive ideas, but where one is better than the other.¹⁹ We plot expected profits as a function of club size for the first seven agents in Figure 6. Agent 1’s profit (red line) exhibits the same pattern as in Figure 5, due to the same underlying mechanism. Agent 2’s profit (black line) is slightly different from the previous case: It follows a similar pattern, but his preferred club is smaller, because his idea is less valuable compared to agent 1’s. This implies that the gain from exclusive access to the other top agent’s idea dominates the matching effect sooner for agent 2 than for agent 1. All the other agents’ profit are decreasing in club size for the same reasons as in Society 1 and 2.

Figure 6. Aristocracy privileges redux.

Under either invitation or expulsion rule, this modification of Society 2 has no effects on club size. However, under elite discretion, the club size is higher compared to Society 2, because agent 1 now has less to gain from exclusive access to agent 2’s idea. Agent 1 thus appreciates more Putnam’s logic in favor of inclusive clubs.

4.3. Society 3: diffuse entrepreneurship

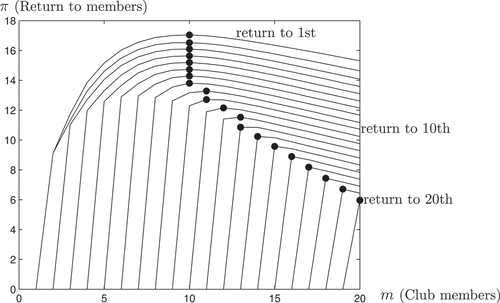
We now turn to analyze a society characterized by relatively homogeneous and productive population of agents. This case resembles a modern society. Everybody is endowed with a productive idea, and differences between ideas are small.²⁰ In this case, all the agents are subject to the two competing forces at play as the club expands: increasing probability of finding a good match to implement their own idea, but also increasing competition for implementation of other ideas. Figure 7 plots the expected profit of all the agents as a function of group size. Interestingly, the first eight agents agree on their preferred club size. In particular, they favor expansion for clubs of small size, but at some point they would like to stop further expansion. The reason is that at some point, each of these first agents is almost sure to find someone able to implement exactly his own idea, and also to get assigned somebody else’s idea. Further expansion beyond this point would lead to increased availability of new ideas, but of lower productivity than those already available. Crucially, further expansion would also lead to dilution of the existing implementation profits due to increased competition for the best ideas available. The profit function is at first increasing, and then decreasing for agents 1 to 12, while the rest of the agents display a pattern similar to the fringe in society 1. In fact, clubs larger than ($m\ge 12$) already ensure high probability of forming high-quality dyads, and adding many more agents only result in much fiercer competition for the insiders.

Figure 7. Diffuse entrepreneurship.

The invitation rule would allow the first eight agents to exactly reach their bliss point, as they all agree about continuing to invite members until size $m^I=10$ is reached. At that point, the two agents who have joined last would like further expansion, but the block of the first eight agents vote against it. In this society, the expulsion rule would instead result in an equilibrium club which encompasses the entire society. In fact, the threat of expulsion forces the ten least productive agents to stick together and vote to save agent 20 in the first vote. They do so because they can foresee that expulsion of agent 20 would be followed by many more, until agents 1–10 would attain $m=10$, which is the bliss point of the first eight agents. The election over expelling agent 20 would thus result in a tie and so in a permanent club of size $m^E=20$. Extrapolating beyond $n=20$, the expulsion rule would always result in clubs as large as at least half of the population.

In this society, Putnam’s and Bourdieu’s logics cohabit within each agent. Nonetheless, large and even all-encompassing clubs in Putnam’s spirit can emerge under the expulsion protocol, sustained by the fear of being evicted. Instead, under elite discretion and invitation rule, the coexistence of the two notions for each agent results in clubs of medium size. A group of relatively homogeneous agents is formed, and the exact club size is the point where Putnam’s logic and Bourdieu’s logic exactly balance. These clubs are relatively inclusive, as the difference between the most and least productive members is large, but also exclusive, as a large part of productive population is left out.

4.4. Society 4: monopoly privilege and bourgeoise

We now revisit Society 1, where one idea stood out as the only profitable. This is a strong assumption if “idea” is to be taken literally, but in a generic interpretation the “idea” could be a feudal privilege to do a particular trade. In Society 1 the holder of the profitable idea would like to see a club as large as possible in order to be sure to have the idea implemented. The implementers, on the other hand, would all of them want to limit the size of the club, in order to maximize their own chance of being the implementor taking part in the profit. It is the sharp distinction between the interest of the innovator and implementors that delivers the sharp result in society 1. No one is part innovator and part implementor.

The situation changes fundamentally if all agents have ideas, albeit with different productivity. More precisely, we here assume that all agents have potentially equally valuable ideas. The idea of agent 1 can again be though of as a feudal privilege to do a particular trade. Such a privilege has a trivial profit potential, and thus it is relatively simple to implement. On the contrary, the other agents’ ideas are ingenious entrepreneurial ideas. Hence, typically a large pool of potential implementors is needed in order to find a productive match. Formally, we assume that $x$ is constant for all agents, but now the probability of a match is heterogeneous: $p_1>p_l=p_i$ $\mathrm{\forall }i\ge 2$. Furthermore, we abstract from mediocre matches, i.e. $\beta =0$.²¹

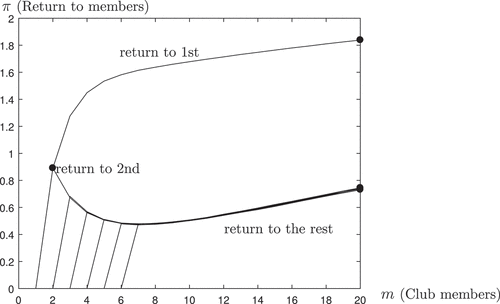
This society is illustrated in Figure 8. The main new feature is that as $m$ increases beyond a certain number, the expected profits of all agents increases in $m$. This follows because when $m$ is sufficiently high, a larger fraction of the $m-1$ ingenious ideas can be implemented. Hence, the expected profits for all agents will increase. The profit function for agent 1 increases for all $m$. It increases quite sharply in the beginning as his own idea is more and more likely to be implemented. It continues to increase, however, as for large $m$ it becomes more and more likely that 1 can also earn income from implementing others’ ideas. The profit relationship for agent 2 (and 3, 4, 5, 6) is first decreasing in $m$. The reason is that for small $m$, the main concern is to be the one who takes part in agent 1’s idea. However, as $m$ grows larger, it becomes yet more likely that someone is able implement agent 2’s own ingenious idea, and that agent 2 can himself implement someone else’s ingenious idea.

Figure 8. Privileges versus ideas.

Society 4 shares many of the features we saw in the simplified framework in section 3. One difference is that here the rents are endogenously generated by agent’s 1 innovation. For the other agents, the competition to have a chance to be matched with this high-value innovation resembles the dilution of the exogenous rents taking place in the simplified model as the club expands. This mechanism is the factor behind the decreasing profile of the profit function, which prevails for small $m$ both in Figure 2 and for the fringe in Figure 8.

What clubs would prevail under different constitutional rules? In the particular configuration with $n=20$, the invitation rule would lead to a club of size $m^I=20$. The reason is that all but agent 2 prefer 20 to any number of members less than 20.²² With a population of size smaller than 20, say $n=16$, also agents 3 and 4 would prefer to limit the expansion. As a result, only agent 3 would be admitted, because at $m=3$ agents 2 and 3 prefer to stop further admittance. The reason is simple enough: None of the feasible $m$ under further expansion yields larger return than $m=3$. If instead $n$ was larger than 20, also agent 2 would support an open club of maximal size. The reason is again simple: When $m$ is very large, the fraction of ingenious ideas implemented will approach unity.²³

(6) $\frac{\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{p}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{s}}{\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{i}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{s}}=\frac{p(m-1)(m-2)}{m-1}=p(m-2).$(6)

As $m$ grows, the number of potential matches outnumbers the number of ideas by orders of magnitude, and, in spite of some overlaps between matches, the expected fraction of implemented matches approaches unity.²⁴

Going back to the example in Figure 8, the matching mechanism in equation (6)(6) $\frac{\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{p}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{s}}{\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{i}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{s}}=\frac{p(m-1)(m-2)}{m-1}=p(m-2).$(6) leads to an open club of maximal size also under expulsion rule. In general, $m^E=n$ as long as $n$ is large enough to ensure enough matching improvement in the all-encompassing club. On the contrary, small societies (e.g, $n=7$) would look like Figure 3: Small expansion potential would prevent the matching return from taking off. In this case, the expulsion rule would lead to exclusive clubs: $m^E<n$.

Finally, elite discretion would lead to an open club. The reason is trivial: Agent 1 follows completely Putnam’s logic, as in Society 1. For all the other agents, Putnam’s and Bourdieu’s notions coexist, and which one prevails depends on the size of the clubs. As in all the previous cases, the mix between Bourdieu’s and Putnam’s logics in the same agents results in the non-monotonicity of their return function. However, here the return function is u-shaped, while it in all the previous cases was hump-shaped.

In this society, the Putnam-inspired notion of opening the club is the predominant force in most cases. The fundamental reason that leads to open clubs here is the fact that newcomers have something valuable to contribute to both sides of the economic exchanges.

4.5. Society 5: aristocracy and bourgeoisie

The u-shaped return schedules of the fringe in Society 4 is a result of the fellow fringe members first representing a congesting factor over the rents attached to agent 1’s privilege. Then, as $m$ gets larger, the fringe represent a yet larger pool of new ideas that with increasing probability can be put to profitable use. The first congestion effect is not relevant for agent 1 as he holds the privilege in the first place. As such, his return schedule is monotonously (weakly) increasing in $m$.

We now modify Society 4 by introducing an additional privileged agent as we did in Society 2.²⁵ In Society 2, having two privileged lead the elite to have a hump-shaped schedule (see Figure 5). Here instead, where we study a case with two privileges and a fringe of ideas, the return schedule of the elite displays again a hump, but it also starts growing again for large enough $m$ (see Figure 9). The explanation behind the hump is the same as before: With more than one privilege, also the aristocracy is affected by the congesting factor caused by the fringe. For very small $m$, the aristocracy benefits from admitting new members as this increases matching. Soon enough however, the increased competition over the other top agent’s privilege offsets the gain from improved matching for their own privilege. To the right of this point, new members represent a congesting factor that dilutes the rent. However, in the present case, for even higher levels of $m$, the return of the two first agents starts increasing again. The reason is the same as the one behind the u-shape of the fringe in Society 4: When $m$ is large the number of potential matches grows faster than the number of ideas. In other words, for large $m$ it is more and more likely that agent 1 and 2 become able to implement at least one idea brought along by the new-comers. In the particular example in Figure 9, the return to the first two agents has a global maximum at $m=5$, a local minimum at $m=11$, and then a local maximum at the corner $m=n=20$.

Figure 9. Aristocracy and bourgeoisie.

The invitation rule will yield $m^I=5$ as the equilibrium: After the club has reached five members all of them will vote against further expansion. The reason is that no club with $m>5$ gives higher returns than what each member get at $m=5$. Thus in this case Bourdieu’s notion dominates, and the club is exclusive. This equilibrium is however sensitive to the exact size of the population. In fact, for $n$ large enough (in this case for $n\ge 23$), all the agents (both elite and fringe) would strictly prefer an open club, $m=n$. The reason has again to do with the matching mechanism in equation (6)(6) $\frac{\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{p}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{s}}{\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{i}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{s}}=\frac{p(m-1)(m-2)}{m-1}=p(m-2).$(6) : For $m$ large enough, virtually all ideas are implemented and each agent earns profit equal to 3.

In the example depicted in Figure 8, the expulsion rule yields open clubs, $m^E=20$. The reason is simple enough: A club of size 20 is strictly preferred to any smaller club by a majority of members, and so no one will be expelled at $m=20$.²⁶ In this case, it is not fear of being expelled that sustains an open club, but rather pure non-strategic economic convenience. For this reason, open clubs will also emerge for societies with $n>16$, where the maximal club size is large enough for the benefit of the matching to outweigh the dilution of the rent from the aristocracy. Smaller societies will remain trapped in Bourdieu’s logic, and yields exclusive clubs.

Similar outcomes will prevail in case of elite discretion: In small societies, i.e. $n<23$, the aristocracy would prefer an exclusive club of only five members. In these cases, they prefer to exchange favors among few members because the benefits from opening the club are not high enough. On the contrary, in large societies, i.e. $n\ge 23$, these benefits are high enough, and the aristocracy always prefer open clubs.

Also in this society, as in Society 4, the fact that everyone has something valuable to contribute on both sides of the exchange facilitates the emergence of open clubs, which can arise under every voting rule. Contrary to the previous case, however, here the aristocracy has a local optimum a low value of $m$.

To summarize, Society 5 Aristocracy and bourgeoisie contains all the main elements that we were interested in. It shows that the same underlying economic environment can generate both inclusive clubs and exclusive clubs. The final outcome depends on the constitutional rule. The size of society, $n$, is a key parameter. Given the productivity parameters, for sufficiently large societies, everyone benefits from embracing the inclusive club. However, in order for a small club to expand sufficiently for all members to benefit from a large club, both the aristocracy and the other club members go through an interval of reduced profits. Hence, in such a case the exclusive club may remain as the equilibrium. The reason is that exclusive club is a local optimum. Then moving to an open club requires both a) imagination about what an open club entails, and b) willingness to wait for the benefits of improved efficiency to materialize. Both these conditions may easily be broken both for a conservative aristocracy and for an elitist bourgeoisie who care about their relative distance to other citizens.

5. Discussion and conclusion

Starting from two different literatures, we have highlighted two roles of social capital: a) as a lubricant for efficient transactions between factors of production; b) as a source of crony favors and access to privileges. Interpreting social capital as a productive asset provided by a social group, these two roles can explain how social capital can both capture closed clubs, where favors dominate, and open associations, where efficiency dominates.

In the stylized case of a club, we have illustrated the forces at play, using a matching algorithm for production combined with voting rules for member invitations and expulsions. We have also brought to the fore the tension between the two aspects of social capital. We have shown how under different voting rules over membership, and starting from different initial conditions, the scope of the club may vary from a closed exclusive one to an open one that embraces all members of society.

The incentives of the insiders to expand or limit the club depend on the relative importance of privileges versus efficiency. For a small club, the privilege aspect tends to be relatively more important, while for larger clubs this aspect is diluted. Therefore, the same underlying primitives can both generate clubs that stay closed and exclusive, and clubs that encompass the entire society.

For a given set of parameters, a club starting in the small may stay small, while, for the same parameters, if the club started large it would remain large. We have identified two separate reasons for all-encompassing clubs to prevail. First, a majority of members of a large club may actually lose from any reduction in club size. Second, given the expulsion voting protocol, a majority of voters may realize that if one member is evicted a process will start whereby they themselves are evicted.

In order for a majority to prefer a large club, the efficiency mechanism must be sufficiently high relative to the privilege. While the rents tend to be diluted with the size of the club, a similar dilution does not necessarily need to affect the efficiency gains. On the contrary, the size of the club may strengthen the efficiency gains. The last two cases analyzed in the paper show that when candidate members bring valuable productive assets (innovations), the initial size of the club is critical. The larger the club, the larger the probability of a productive match with the newcomers, and the more the newcomers contribute to the total production of the club. An innovation that is productive in a large club may be virtually unproductive in a small club, if it is not trivial to put at use. Therefore, a small society may generate small exclusive clubs, while large societies may generate all-encompassing open clubs.

Acknowledgment

For comments and suggestions we are grateful to Marta Crispino and Gaute Torsvik. All errors are our own. This paper is part of the research activities at the project European Strains at ESOP - Centre for the study of Equality, Social Organization, and Performance at the Department of Economics, University of Oslo. European Strains is funded by the Research Council of Norway through its Europe in Transition funding scheme, project number 227072/F10. The views expressed in this paper do not necessarily reflect those of the Bank of Italy. Declarations of interest: none.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the Research Council of Norway [227072/F10].

Notes

¹ Complete quote: “the aggregate of the actual or potential resources which are linked to possession of a durable network of more or less institutionalized relationships of mutual acquaintance and recognition – or in other words, to membership in a group – which provides each of its members with the backing of the collectivity-owned capital, a ‘credential’ which entitles them to credit, in the various senses of the word.”

² Interestingly Haselmann et al. (2018) cite Putnam’s work, but not Bourdieu’s, confirming that the contribution of the former had more fortune among economists.

³ In our implementation, the optimal allocation is found using the Hungarian algorithm developed by Kuhn (1955) and Munkres (1957).

⁴ In particular, she consider two rules: open access where everyone can join; and group formation by majority voting where the median voter has agenda-setting powers.

⁵ The fixed rent is derived endogenously in the complete setup in Section 3 where we introduce heterogeneity between workers’ ideas. This will give an incentive to limit the number of members in the club.

⁶ From the Binomial distribution.

⁷ It is easy to check that $f(a\cdot m)>a\cdot f(m)\mathrm{\forall }a>1$.

⁸ Moreover, the condition for the hump of the right hand side to be relevant (that it, is to the right of $m=1$) is that its value at $m=3$ is larger than its value at $m=2$. The condition for this is $p<3/4$.

⁹ For example, the sub-matrix obtained by deleting the first row and the first column is a club, but the sub-matrix obtained deleting the first row and the second column is not.

¹⁰ This assumption could be modified in a number of ways. In particular, shares could be determined by outside options of the participants of the dyad. From our set up it is not a priori clear who has most to lose from dropping out. An exogenous split of 50/50 could be interpreted as a focal point solution across environments.

¹¹ We use a Matlab implementation, developed by Yi Cao.

¹² At least 10,000.

¹³ $x_1=3$, and $x_i=0^{+}\mathrm{\forall }i\ge 2$. All agents are potentially equally able to perfectly implement other agents’ ideas: $p_i=p=1/3\mathrm{\forall }i$. Ideas handed over to a mediocre implementor yield one fifth of their value, that is $\beta =1/5$.

¹⁴ The mechanism is analogous to the rent dilution effect described in the simplified framework of section 2.

¹⁵ The proof of this result and all the other proofs are collected in Appendix A.

¹⁶ See Appendix A for details.

¹⁷ In particular, we simulate the scenario with $x_1=x_2=3$ and $x_i=0^{+}\mathrm{\forall }i=3,\dots ,20$. Moreover, $\beta =1/5$ and $p=1/3$.

¹⁸ See Appendix A.

¹⁹ In particular: $x_1=3$, $x_2=2.5$, $x_i=0^{+}\mathrm{\forall }i=\ge 3$, $\beta =1/5$, and $p=1/3\mathrm{\forall }j$.

²⁰ In particular: $x_1=20$, $x_i=x_{i-1}-1\mathrm{\forall }i>1$, $\beta =1/5$, and $p=1/3\mathrm{\forall }j$.

²¹ The parameters in the simulation are: $x=3\mathrm{\forall }i$; $\beta =0$; $=[7/12,1/67,\dots 1/67]$.

²² If voting over club expansion entailed a time delay, and if there also was discounting, the expansion of the club in Figure 8 could instead get stuck at several intermediate sizes. Starting from club sizes between 3 and 7, expansion to one additional member would not be immediately profitable to a majority of the existing members.

²³ The privilege of agent 1 will be implemented as well.

²⁴ As such, all the profit schedules in Figure 8 will converge to 3 as $m$ grows large.

²⁵ Formally, we assume: $x=3\mathrm{\forall }i$; $\beta =0$; $=[7/12,7/12,1/67,\dots 1/67].$.

²⁶ It is only 1, 2, 3, 4, and 5 who prefers a $m<20$.

Appendix A

Proofs

A.1 Proofs of Society 1

Voting equilibrium under expulsion rule: $m^E=18$. We proceed by backward induction, beginning with the vote about expelling agent number 2 in $x$. Recall that the first agent votes against expulsion of every other agent, because her profit is increasing in club size. Therefore, in every vote at least two agents vote against expulsion: the first agent and the agent whose expulsion is under scrutiny. This implies that all the clubs with size $m\le 4$ are stable equilibria. Define the stable equilibrium as ${\hat{m}}_v^E$, where $v$ indexes from the smallest to the largest stable equilibrium (so ${\hat{m}}_1^E$=2, ${\hat{m}}_2^E$=3 and ${\hat{m}}_3^E$=4.)

Lemma 1.1 At the vote about expelling agent $m$ in $x$, all the agents in $x$ indexed between 2 and the biggest stable equilibrium ${\hat{m}}_v^E$ smaller than $m$, vote for expulsion. All other agents vote against expulsions.

Proof 1.1 The aforementioned agents know that they will not be expelled if the voting proceeds further: They sit on or to the left of the next smallest stable equilibrium, and their profit functions are strictly decreasing in $m$. All other agents know that they will be expelled if the voting proceeds further, so they would like to stop the vote dynamic.

Lemma 1.2 If agent in position $x$ vote for expulsion, then all agents with position $1<i<x$ vote for expulsion as well.

Proof 1.2 Follows from Lemma 1.1.

Lemma 1.3 All the stable equilibria ${\hat{m}}_v^E$ larger than 4 are characterized by the same number of agents voting in favor and against expulsion (a tie).

Proof 1.3 Part I: If there is a majority of agents in favor of expulsion of agent $m$, expulsion occurs, and so the voting continues. Thus, this can not be a stable equilibrium. Part II: Suppose there is instead a majority of agents against the expulsion when voting about agent $m$. This implies that also the next vote about expelling agent $m-1$ would have a majority against expulsion, or result in a tie. It is thus not optimal for agent $m-1$ to vote against expulsion, as his profit function is decreasing in club size. If this is true, it is not optimal for any of the agents to the left of $m-1$ (excluding agent 1) as well, by Lemma 1.2. Thus, there can not be a majority against expulsion (as this option only attracts the vote of agent $m$ and agent 1), let alone this configuration be a stable equilibrium.

The lemmas imply that the stable equilibria ${\hat{m}}_v^E$ larger than 4 are defined by the following equation:

(7) ${\hat{m}}_{v-1}^E-1={\hat{m}}_v^E-{\hat{m}}_{v-1}^E+1,$(7)

where on the left-hand side is the number of agents voting for expulsion, and on the right-hand side is the number of agents voting against. Rearranging, we obtain the difference equation that defines the sequence of stable equilibria:

(8) ${\hat{m}}_v^E=2{\hat{m}}_{v-1}^E-2,$(8)

together with the initial condition ${\hat{m}}_3^E=4$. The unique stable equilibrium $m^E$ in a population of size $n$ is the largest stable equilibrium that satisfies ${\hat{m}}_v^E<n$. Table A1 reports the outcome of the votes over every agent in a population of size $n$.

Table A1. Society 1, sequence of voting outcomes under expulsion rule.

Voting	Favor	Against	Equilibrium
over	expulsion	expulsion	outcome
3	2	1,3	Game stops
4	2,3	1,4	Game stops
5	2–4	1,5	Expulsion
6	2–4	1,5,6	Game stops
7	2–6	1,7	Expulsion
8	2–6	1,7,8	Expulsion
9	2–6	1,7–9	Expulsion
10	2–6	1,7–10	Game stops
11	2–10	1,11	Expulsion
12	2–10	1,11,12	Expulsion
13	2–10	1,11–13	Expulsion
14	2–10	1,11–14	Expulsion
15	2–10	1,11–15	Expulsion
16	2–10	1,11–16	Expulsion
17	2–10	1,11–17	Expulsion
18	2–10	1,11–18	Game stops
19	2–18	1,19	Expulsion
20	2–18	1,19,20	Expulsion

A.2

Proofs of Society 2

Voting equilibrium under expulsion rule: $m^E=16$. Define $m^{\ast }$ the club size that maximizes the expected profit for agent 1 and 2, and $\pi (m^{\ast })$ the corresponding profit level. For $m\le m^{\ast }$, at least three agents (agents 1, 2 and the one under scrutiny) always vote against expulsion. This implies that all clubs of size $m\le 6$ are stable equilibria, as long as $m^{\ast }\ge 6$, which is the case in Scenario 2. For $m>m^{\ast }$, the voting behavior of the first two agents is influenced by strategic concerns: They vote against expulsion, if and only if the expected profits obtained at the current club size are greater than or equal to the profits that they would obtain in a club of size equal to the next smaller stable equilibrium. The voting behavior of all the other agents is the same as in Scenario 1.

Lemma 2.1 At the vote about expelling agent $m$ in $x$, all the agents in $$ indexed between 3 and the biggest stable equilibrium ${\hat{m}}_v^E$ smaller than $m$, vote for expulsion.

Proof 2.1 Almost identical to proof 1.1.

Lemma 2.2 All the stable equilibria ${\hat{m}}_v^E$ larger than 6 are characterized by the same number of agents voting in favor and against expulsion (a tie).

Proof 2.2 Almost identical to proof 1.3.

Lemma 2.3: It exists at most one stable equilibrium ${\hat{m}}_v^E$ such that ${\hat{m}}_v^E>m^{\ast }$ and such that agent 1 and 2 vote against expulsion.

Proof 2.3: $\mathrm{\forall }m>m^{\ast }$, agent 1 and 2 would like to block the club size at $m$ (vote against expulsion) if and only if the profits at that $m$ are greater than the profits at the next smallest stable equilibrium. For this to be true, the next smallest equilibrium must be smaller than $m^{\ast }$, otherwise agents 1 and 2 would strictly prefer to shrink the club further (vote for expulsion), as their profit functions are strictly decreasing in club size for $m>m^{\ast }$.

The sequence of stable equilibria is defined by:

(9) $\left(\begin{array}{c}{\hat{m}}_{v-1}^E-2={\hat{m}}_v^E-{\hat{m}}_{v-1}^E+2\mathrm{i}\mathrm{f}{\hat{m}}_v^E\le m^{\ast }\\ {\hat{m}}_{v-1}^E-2={\hat{m}}_v^E-{\hat{m}}_{v-1}^E+2\mathrm{i}\mathrm{f}{\hat{m}}_v^E>m^{\ast }\\ \text{amp}\pi ({\hat{m}}_{v-1}^E)\le \pi ({\hat{m}}_v^E)\text{amp}{\hat{m}}_{v-1}^E\le m^{\ast }\\ {\hat{m}}_{v-1}^E={\hat{m}}_v^E-{\hat{m}}_{v-1}^E\mathrm{i}\mathrm{f}{\hat{m}}_v^E{m}^{\ast }\\ \text{amp}\pi ({\hat{m}}_{v-1}^E)>\pi ({\hat{m}}_v^E)\text{amp}{\hat{m}}_{v-1}^E>m^{\ast },\end{array}\right.$(9)

where on the left-hand size of the equations is the number of agents voting for the expulsions, and on the right-hand size is the number of those voting against. Rearranging, we obtain the difference equation that defines the sequence of stable equilibria larger than 6:

(10) ${\hat{m}}_v^E=\left(\begin{array}{c}2{\hat{m}}_{v-1}^E-4\mathrm{i}\mathrm{f}{\hat{m}}_v^E\le m^{\ast }\\ 2{\hat{m}}_{v-1}^E-4\mathrm{i}\mathrm{f}{\hat{m}}_v^E>m^{\ast }\text{amp}\pi ({\hat{m}}_{v-1}^E)\le \pi ({\hat{m}}_v^E)\text{amp}{\hat{m}}_{v-1}^E\le m^{\ast }\\ 2{\hat{m}}_{v-1}^E\mathrm{i}\mathrm{f}{\hat{m}}_v^E>m^{\ast }\text{amp}\pi ({\hat{m}}_{v-1}^E)>\pi ({\hat{m}}_v^E)\text{amp}{\hat{m}}_{v-1}^E>m^{\ast },\end{array}\right.$(10)

together with the initial condition, ${\hat{m}}_5^E=6$.

The profits of agents 1 and 2 as function of club size in our simulation are as follows:

$\pi (m)=[01.3921,1.4718,1.5322,1.5866,1.6202,1.643,1.6477,$

$1.6494,1.6415,1.6381,1.6301,1.6212,1.6142,1.6077,$

(11) $1.6004,1.5956,1.5885,1.585,1.5791],$(11)

thus $m^{\ast }=9$. The largest stable equilibrium smaller than $m^{\ast }=9$ is equal to 8. The next larger equilibrium defined by ${\hat{m}}_v^E=2{\hat{m}}_{v-1}^E-4$ is a club of size twelve. However, $m=12$ does not satisfy the equilibrium conditions, because agent 1 and 2 attain higher profits in a club of eight ($\pi (8)=1.6477$) than in a club of twelve ($\pi (12)=1.6301$). Therefore, to the right of ${\hat{m}}_v^E=8$, the sequence of stable equilibria follows the equation ${\hat{m}}_v^E=2{\hat{m}}_{v-1}^E$, and so is: 16, 32, 64, etc. The unique stable equilibrium $m^E$ in a population of size $n$ is the largest stable equilibrium that satisfies ${\hat{m}}_v^E<n$. Thus, $m^E=16$. The stable equilibria for all the $n<540$ are plotted in Figure A1.

Figure A1. Aristocracy, voting equilibria under expulsion rule.