Nanorings in planar confinement: the role of repulsive surfaces on the formation of lacuna smectics

ABSTRACT

We study the structure and liquid-crystalline phase behaviour of a model of confined non-convex circular soft-repulsive nanorings in a planar slit geometry using molecular-dynamics simulation. The separation distance between the structureless parallel soft-repulsive walls is made large enough to allow for the formation of a distinct bulk phase in the central region of the box which is in coexistence with the adsorbed fluid thus allowing the analysis of single-wall effects. As the density of the particles is increased, the fluid adsorbs (wets) onto the planar surfaces leading to the formation of well-defined smectic-A layers with a spacing proportional to the diameter of the rings. An analysis of the nematic order parameter at distances perpendicular to the surface reveals that the particles in each layer exhibit anti-nematic behaviour and planar (edge-on) anchoring relative to the short symmetry axis of the rings. This behaviour is in stark contrast to the behaviour observed in convex disc-like particles that have the tendency to form nematic (discotic) structures with homeotropic (face-on) anchoring. The smectic phases formed by nanorings in the bulk and under confinement are characterised by the formation of low-density layered liquid-crystalline states with large voids, referred to here as lacuna smectic phases. In contrast to what is typically found for confined liquid-crystalline systems involving convex particles, no apparent biaxiality is found for nanorings in planar confinement. We argue that formation of the low-density lacuna smectic layers with planar anchoring is a consequence of the non-convex shape of the circular rings that allow for interpenetration between the particles as observed for nanorings under bulk conditions [C. Avendaño, G. Jackson, E.A. Müller and F.A. Escobedo, Proc. Natl. Acad. Sci. U.S.A. 113, 9699 (2016); H.H. Wensink and C. Avendaño, Phys. Rev. E 94, 062704 (2016)].

GRAPHICAL ABSTRACT

KEYWORDS:

• Lacuna smectics
• surface ordering
• liquid crystals
• non-convex ring-like particles
• molecular dynamics

1. Introduction

The shape of colloidal particles is one of the key features dictating their collective properties [1,2]. Particle shape gives rise to the formation of a myriad of structures including the formation of exotic liquid crystals, rotator phases, quasicrystals and solid and crystalline phases [3–7]. For liquid-crystalline systems in particular, Onsager provided a theoretical explanation for the isotropic–nematic phase transition observed in purely repulsive particles with anisotropic uniaxial shapes representative of rod-like and disc-like colloids [8]. Onsager's seminal framework of 1949 is based on a free-energy functional that depends on the single-particle orientational distribution function. In Onsager's theory the free energy is represented as a virial expansion up to the second-virial coefficient, which is known to be highly accurate for rod-like particles in the limit of high anisotropies, i.e. infinitely thin rods [9]. The second-virial theory does not, however, capture the low-density limit of disc-like particles due to the non-vanishing higher terms in the virial expansion [10–12]. Onsager showed that the stability of the nematic phase is determined by a competition between the orientational entropy, which favours the formation of randomly oriented isotropic phases, and the packing entropy, which promotes the alignment of the particles by enhancing the free volume. Despite the success of Onsager's and subsequent density functional theories to describe the formation of liquid-crystalline phases in systems of lyotropic colloids [13–25], the first unequivocal observation of liquid-crystalline phases by essentially exact numerical computer simulation methods had to wait until the mid-1980s. The pioneering computer simulations of Frenkel and co-workers for systems of hard anisotropic particles confirmed the earlier theoretical predictions of the formation of not only nematic and discotic orientationally ordered phases in rod-like and disc-like particles but also of stable smectic (layered) and columnar (stacked) phases [1,11,26–33].

The presence of external forces, as a result of solid surfaces, for example, can have a strong influence on the properties of colloidal particles due to the breaking of space symmetry whereby the translational and orientational properties of the particles are dictated by interactions with the surface. Non-spherical particles confined in narrow planar slits are found to exhibit the formation of a variety of structures with symmetries not observed under bulk conditions [34–42].

The effect of ordering of particles in contact with a single planar wall has been addressed by computer simulation of systems in planar slit confinement where the separation between the walls is large enough to allow a clear distinction between particles near the surface (surface region) and particles far from and not influenced directly by the surface (bulk region). The effects induced by solid surfaces include surface ordering, anchoring’ and wetting [43]. Surface ordering refers to the structural and orientational properties of the film formed at the surface where the direct interaction of the wall with the particles influences their translational and orientational order. The term anchoring is used to denote the direct effect the solid surface has on the orientation of the particles in the vicinity of the surface, which is no longer arbitrary as in the case of bulk systems. Depending on the orientation of the system with respect to the direction of the wall, three different situations are commonly observed: planar, homeotropic, and tilted anchoring. In the case of flat repulsive disc-like particles, planar anchoring on a hard wall refers to the situation where the orientation of the (short) symmetry axis of the particles is parallel to the surface, i.e. particles lie ‘edge-on’ relative to the surface. The most common situation for disc-like particles is homeotropic alignment where the orientation of the symmetry axis of the particles is perpendicular to the surface, i.e. the particles lie ‘face-on’ relative to the surface.

One of the simplest models for studies of surface effects in colloidal systems is an ensemble of hard spheres confined between two planar structureless hard walls [44–51]. Despite the apparent simplicity of this model, the wetting and adsorption of hard spheres on a solid surface is not a trivial problem since the properties of athermal systems of this type are driven purely by entropic considerations. The simulation study reported by Dijkstra [48], for example, confirmed that hard spheres indeed exhibit complete wetting of the crystal phase represented by a vanishing contact angle. When the separation between the two walls in the slit is large enough to allow for the formation of a clear bulk region, the simulations are able to represent single-wall phenomena. The additional orientational degrees of freedom of non-spherical particles under geometrical confinement lead not only to interesting translational ordering but also to orientational ordering near the wall–fluid interface. van Roij and co-workers have reported extensive simulation studies of rod-like particles, modelled as hard spherocylinders, confined in planar slits where the particles partially wet the planar surfaces and exhibit planar anchoring with enhanced nematic ordering and biaxiality [52–54]. Similar nematisation phenomena have been observed in mixtures of rods and spheres [55,56]. Experiment, theory, and simulation of disc-like particles under confinement have also been reported [57–59]; in the particular case of infinitely thin discs, complete wetting of the wall by the nematic phase is observed with homeotropic anchoring as expected from the geometry of the particles.

Advances in synthetic protocols for the fabrication of colloidal particles with complex morphologies have triggered new simulation studies aiming at improving our understanding of the phase behaviour of particles with highly non-convex geometries [60–67]. Examples include branched particles [38,41,68], dimpled, bowl-like and lens-like particles [69–76], non-convex platelets [77,78], and planar rings [79–81]. Modelling non-convex particles generally presents an added challenge due to the complex interactions that emerge due to the complexity in shape such as interlocking, entanglement, and interpenetration, which can hinder the equilibration of the system [67]. For certain non-convex particle shapes, however, these features can be harnessed to promote order in the system. For example, Miszta et al. [68] have shown that interlocking in branched octapod-shaped particles is responsible for the self-assembly of superlattices, while lock-and-key interactions in dimpled particles can lead to the formation of colloidal living polymers [69]. Similarly, Vanakaras and Photinos [82] have examined fan-shaped hard particles, represented as three infinitely thin discs fused along a common diameter, which are found to form stable smectic phases driven by the large interpenetration between the particles. We have also recently demonstrated using computer simulation and a second-virial Onsager theory that rigid and planar colloidal rings can form liquid-crystalline smectic phases with unusually high free volumes driven by interpenetration and interlocking of the particles [81,83]; here we will refer to these low-density smectic phases as ‘lacuna smectics’. Understanding how the complex interactions between non-convex particles are affected by the presence of surfaces has not to our knowledge yet been studied. In our current work, we examine the surface ordering in a non-convex model of rigid-planar rings under slit confinement with wall separations that are large enough to allow the formation of a distinct bulk region away from the walls.

2. Molecular model and simulation details

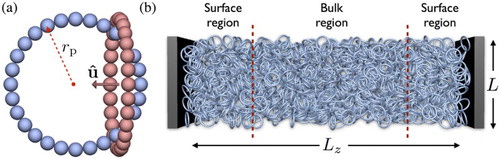
The rings are modelled as rigid-planar necklaces comprising tangent beads of diameter σ [80,81]. This model, which is depicted in Figure 1, leads to a ring of radius (corresponding to the distance from the centre of the rings to the centre of any of its spherical beads). The orientation of the particles is fully characterised by the unit vector , which is perpendicular to the plane of the ring. The bead–bead interactions are described with a soft-repulsive potential based on the Lennard-Jones (LJ) potential truncated and shifted to zero at the cut-off distance . This potential is commonly referred to as the Weeks–Chandler–Andersen (WCA) potential [84,85]. Particles are placed in a rectangular box of volume and area , and periodic boundary conditions are applied only in the x and y directions. The confinement along the z direction is represented by two soft-repulsive WCA walls (characterised by the same LJ parameters as the beads) placed at and relative to the centre of the box, respectively. For our choice of Gibbs dividing surface, the overall volume of the confined system is defined to include the two regions inaccessible to the ring particles in layers of thickness close to the two walls. Systems of N=4000 nanorings are simulated to study the nanorings under confinement. The dimensions of the simulation box in the x and y directions are fixed at while the longitudinal length is adjusted to give the desired value of the volume (packing) fraction η. Systems comprising N=8000 nanorings and transverse box dimensions are used to investigate the effect of the wall separation on the phase behaviour of the system under confinement. For both system sizes, the molecular-dynamics simulations are initialised with the lowest density state studied and the resulting final equilibrium configuration is used as the starting point for the following state of higher density for which the longitudinal dimension is linearly adjusted during the equilibration period until the desired value of is obtained. For each state, an equilibration run of timesteps is used to bring the repulsive walls to the desired position, followed by an equilibration run of timesteps at constant density to allow the relaxation of the structures. Ensemble averages are then collected from simulations spanning between and timesteps.

Figure 1. (a) Model of circular nanoring of radius formed from spherical beads of diameter σ. The orientation of the particles is fully characterised by the unit vector , which is perpendicular to the plane of the ring (this unit vector is shown only for one ring). Due to the large internal cavity of the particles, interpenetration between a pair of particles is possible as shown in the figure. (b) Configuration of nanorings confined between two soft-repulsive walls separated by a longitudinal distance along the z direction; the planar transverse area of each wall is .

Dimensionless units are used throughout: the temperature, number density, packing fraction, and time are defined as , , , and , where is the Boltzmann factor, T is the absolute temperature, ε is the well-depth energy of the underlying LJ potential, t is the time, and m is the mass of each WCA spherical bead. In a similar manner, all distances are given in units of . The molecular-dynamics simulations are performed in the canonical NVT ensemble by employing Nosé–Hoover dynamics [86,87]. The equations of motion are integrated using the velocity-Verlet integrator using a time step of [88]. All simulations are carried out using the LAMMPS molecular-dynamics package [89].

To study the translational and orientational ordering of the confined system, the system is divided into bins along the z direction and statistics of the number of particles in each bin are collected. The packing fraction profile is determined from (1) where is the position of bin j, is the number of ring particles in bin j and is the width of the bin which is kept at in all cases.

Due to the anisotropic nature of the particles, the local ordering of the system at position z is also analysed using the local nematic order parameter profile , which is calculated from the local second-rank Saupe ordering tensor [11] given by (2) where is the unit tensor. Diagonalisation of the tensor leads to three corresponding eigenvalues (); the (local) nematic order parameter corresponds to the largest eigenvalue. The biaxial order parameter profile is obtained as the difference between the two smallest eigenvalues of the tensor , and used to analyse the degree of order in the direction perpendicular to the director of the system.

The surface adsorption Γ of the system is quantified from (3) where is the number density of the bulk region formed away from the wall and is the corresponding packing fraction. Surface adsorption provides information about the excess number of particles per unit area close to the surface relative to the number in the bulk of the sample; for our choice of Gibbs dividing surface will be positive for an accumulation of particles (wetting) and negative for a depletion of particles (dewetting).

3. Structural, orientational and adsorption properties of nanorings under planar confinement

The bulk phase diagram for the model of circular nanorings shown in Figure 1 has been studied previously by molecular-dynamics simulation where the system was found to exhibit a first-order phase transition from an isotropic (Iso) state ( and ) to a liquid-crystalline smectic-A (SmA) state ( and ) [81]. The SmA phase formed by rigid-planar nanorings is characterised by negative values of the nematic order parameter indicating the particles adopt orientations that are perpendicular to the order of the system, i.e. the particles are oriented perpendicular to the direction of the smectic layers corresponding to anti-nematic order [80,81,83]. Furthermore, the unusually low values of the packing fraction reveal the formation of lacuna smectic structures with high free volumes, which is a consequence of the non-convex shape of the particles that prevents them from packing efficiently [79].

We first discuss the phase behaviour of a system comprising N=4000 nanorings confined in a planar slit geometry with a transverse length of . The findings for the lowest density state analysed, corresponding to a longitudinal length of , can be used to highlight the main phenomena taking place at the wall–fluid interface. The packing fraction (density) and the nematic order parameter profiles along the z direction perpendicular to the planar walls for this low-density state are shown in Figure 2(a,b). Away from the surface, the packing fraction profile becomes flat with an average value of the bulk packing fraction of indicating the formation of a bulk region with a negligible value of the nematic order parameter () that corresponds to an isotropic phase. Near the surface, the packing fraction profile exhibits the formation of three clear peaks. The first small peak, located at a distance of from the wall, corresponds to the adsorption of few rings forming a thin wetting layer with perfect homeotropic (face-on) ordering as indicated by the corresponding peak in the nematic order profile with a magnitude of . The predominant feature in the packing fraction profile is observed at a distance of from the wall with a corresponding peak of in the nematic order parameter profile. This peak is associated with a well-defined adsorption layer of nanorings with planar (edge-on) ordering. The formation of layers with planar ordering by repulsive-planar particles on a repulsive wall is unusual [58]. Typically, one would expect planar particles to adsorb on a planar wall with homeotropic ordering and to exhibit a certain degree of nematisation. The unusual surface ordering behaviour observed in rigid-planar nanorings is a consequence of the non-convex geometry of the particles where the interpenetration locks the particles in well-defined layers with anti-nematic order: the particles are oriented perpendicular to the direction of the layer, which in this case is along the z direction, yielding negative values of the nematic order parameter [80,81,83]. It is important to point out that Poier et al. [90] have also observed the formation of layers with planar anchoring in simulations of stiff ring polymers confined by hard walls. The geometry of these ring–polymer systems indeed share similarities with our nanoring model, the main difference being that the ring polymers are modelled as penetrable disc-like objects. In our model, the maximum allowed interpenetration between two rings corresponds to the arrangement shown in Figure 1(a). Notwithstanding, the similar behaviour of both models suggests that the large ring cavity is the main feature driving the formation of the planar ordering. The third peak observed in the packing fraction profile shown in Figure 2(a) at a distance of from the wall reveals the beginning of the formation of a third disordered layer with a corresponding value of the nematic order parameter of which is characteristic of an isotropic state. The distance between the third and the second peak is approximately twice the radius (corresponding to the diameter) of the ring. It is important to note that the nematic order parameter profile also shows a well-defined peak at with a magnitude of . This peak develops at the same position as the kink observed in the packing fraction profile indicating a small number of rings with homeotropic ordering localised (trapped) between two main layers. These key features observed in both the packing fraction and nematic order parameter profiles are also evident in the snapshot shown in Figure 3(b) where a small number of particles, shown with darker shading, are clearly seen to be trapped between the two main layers and also between the wall and the first layer. The biaxial order parameter profile shown in Figure 2(b) suggests negligible biaxial order at all distances, with two shallow peaks of magnitude at the locations of the layers: and . This behaviour reflects the lack of any degree of biaxiality at least for this low-density state.

Figure 2. (a) Packing fraction profile and (b) nematic and biaxial order parameter profiles along the z direction for a system comprising N=4000 nanorings in planar confinement with a transverse box length of and a longitudinal length of obtained by molecular-dynamics simulation. The three vertical dashed lines indicate the position of the main peaks in the packing fraction profile, and the vertical dotted line indicates the position of a kink formed between the second and third peaks.

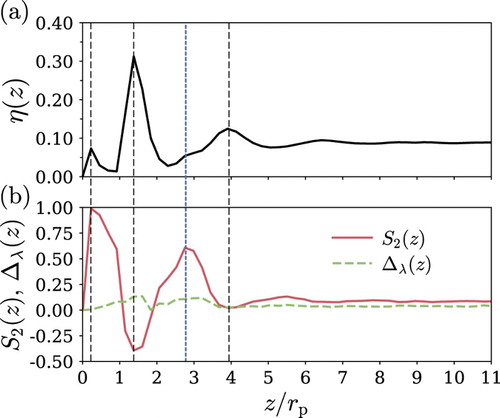
Figure 3. Representative configuration of systems comprising N=4000 nanorings in planar confinement with a transverse box length of obtained by molecular-dynamics simulation. From bottom to top, the transverse box lengths are 65.4, 59.2, 56.9, 54.5, and 52.3. Particles are shaded according to their orientations with respect to the normal to the planar wall. Only half of the system is shown as the system symmetric along z.

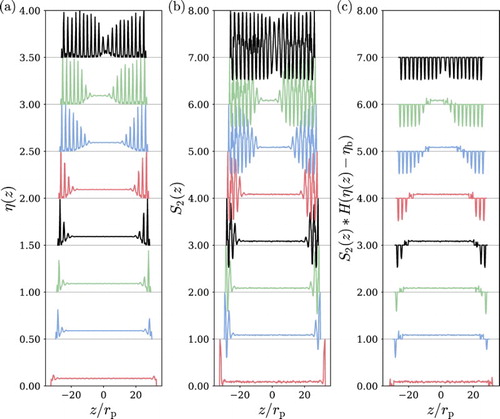
We proceed by examining the surface ordering and phase behaviour of the confined nanoring systems for states of increasing density. The results for the packing fraction and nematic order parameter profiles for different values of the longitudinal box length are shown in Figure 4(a,b). These values of all lead to bulk values of the packing fraction which are below that observed for the isotropic–smectic phase transition in bulk systems, which corresponds to . It is clear that as the density of rings in the system is increased the number of layers with homeotropic ordering also increases, with a separation between the peaks which is approximately twice the radius of the rings. The formation of these peaks appears to be continuous in nature, with the number of layers increasing rapidly as a function of the wall separation . It is clear from the profiles that the system progressively forms a lacuna SmA liquid-crystalline phase with increasing numbers of layers growing along the direction perpendicular to the wall; each layer exhibits anti-nematic behaviour with characteristic negative values of the nematic order parameter. Representative configuration of these systems for four different box dimensions are shown in Figure 3. An analysis of the nematic order parameter profile also indicates that small numbers of particles are trapped between the layers hence the regular oscillations between (smectic layers with planar ordering) and (trapped particles with homeotropic ordering). The number of particles trapped between layers is very small as indicated by the small peaks observed in the packing fraction profile. Indeed, these trapped particles can be considered as defects, which have also been observed in smectic phases formed by the same model in bulk systems [81]. To aid the identification of the smectic layers, the information related to the trapped particles has been removed from the nematic order profile by using a Heaviside function. In this case, when the packing fraction is below the bulk packing fraction then the local nematic order parameter is taken to be zero, otherwise the order parameter is left unmodified. The resulting values of the local nematic order parameter after this process are shown in Figure 4(c), where it is clear that smectic layers with anti-nematic ordering are formed. For longitudinal box dimensions of and the systems clearly form large and stable regions of smectic phase close to the surface in coexistence with an isotropic phase in the bulk region. As the longitudinal box dimension is decreased to the isotropic region disappears and the system exhibits an apparent discontinuous phase transition to a SmA phase which is stable across the entire system. It is also interesting to note that the density of the smectic layers, particularly near the walls, does not exhibit a dramatic increase as the density of the system is increased, which could be due to the very low overall packing fractions of the system. The packing fraction profile for the highest density state also reveals that the two smectic layers at the centre of the system are not as well defined as in the rest of the system: this is a consequence of the longitudinal box length being incommensurate with the spacing of the layers. The bulk packing fraction of this smectic phase is , which is lower than the packing fraction of for the smectic phase at coexistence obtained for bulk systems [81]; this suggests that the separation between the repulsive walls in the planar slit is still not quite large enough to completely neglect confinement effects. Note, however, the exact point of the isotropic–smectic transition was not determined to high precisions in [81] and only approximate boundaries were reported. An analysis of the biaxial order parameter profile (results not shown) reveals that the smectic phases remain uniaxial at all of the densities considered, with a maximum value of for all of the layers formed, even those near the walls. This behaviour is in agreement with the observation that the surface density peaks in the packing fraction profile are scarcely enhanced by the presence of the walls.

Figure 4. (a) Packing fraction and (b) nematic order parameter profiles along the z direction for systems comprising N=4000 nanorings in planar confinement with a transverse box length of obtained by molecular-dynamics simulation. From bottom to top, the values of the longitudinal box length are 65.4, 59.2, 58.1, 56.9, 55.7, 54.5, 53.4, and 52.3. The corresponding bulk packing fractions for each box dimension correspond to 0.0805, 0.0883, 0.0901, 0.0914, 0.0926, 0.0927, 0.0930, and 0.1006. In Figure (c), the orientational order of the small concentration of trapped particles in between layers is removed from using the Heaviside function of the difference between the local packing fraction and the bulk packing fraction. The profiles in the series (a) to (c) are each shifted upwards by 0.5, 1.0 and 1.0, respectively, to aid visualisation. The thin horizontal lines are drawn to indicate the baselines.

We have also studied a larger system comprising N=8000 nanorings and a transverse box length of to analyse the effect that large wall separations have on the phase behaviour. The resulting packing fraction and nematic order profiles for several values of the longitudinal box length are shown in Figure 5. The system exhibits a similar surface behaviour as seen for the smaller system with SmA layers formed along the z direction exhibiting planar anchoring and anti-nematic behaviour. However, the larger system exhibits an isotropic–smectic transition at a higher packing fraction than is found for the smaller system. The bulk packing fraction of the smectic phase is which is closer to the transition densities observed in bulk systems. This suggests that the separation between the repulsive walls is large enough to probe single-wall effects, with the central region of the box essentially corresponding to that of the bulk phase. Representative configurations for this system below and at the isotropic–smectic phase transition are shown in Figure 6. As in the case of the smaller system, the amplitude of the density profiles of the well-developed SmA layers appears to remain constant regardless of the wall separation thus indicating that layer compression is minimal. This behaviour is different to what is typically observed in systems of convex spheres, rods, or discs where the adsorbed layers in contact with the walls usually exhibit higher densities; in some cases, solid-like behaviour is observed. As in the case of the smaller system, we can see from Figure 5(b) that the larger system exhibits oscillations in the nematic order parameter between , indicating the formation of smectic layers, and corresponding to the particles trapped between layers. The spacing between the peaks defining the SmA layers is again about twice the radius of the rings, which is consistent with the findings of the bulk simulations [81]. As in the case of the smaller system, the formation of the smectic layers is more evident in Figure 5(c) after the information relating to the order of the trapped particles is removed. The density profiles for the system with N=8000 are clearly less symmetrical than for the system with N=4000 despite the extremely long simulation runs. This is, however, not surprising since very small density fluctuations allow for independent growth of the smectic layers due to the very low packing fractions involved.

Figure 5. (a) Packing fraction and (b) nematic order parameter profiles along the z direction for systems comprising N=8000 nanorings in planar confinement with a transverse box length of obtained by molecular-dynamics simulation. From bottom to top, the values of the longitudinal box length are 186.3, 182.1, 178.2, 174.4, 170.8, 167.3, 163.9, 160.7, and 157.9. The corresponding bulk packing fractions for each box dimension correspond to 0.0883, 0.0900, 0.0916, 0.0927, 0.0930, 0.0929, 0.0931, 0.0929, and 0.1048. In Figure (c), the orientational order of the small concentration of trapped particles in between layers is removed from using the Heaviside function of the difference between the local packing fraction and the bulk packing fraction. The profiles in series (a) to (c) are each shifted upwards by 0.5, 1.0 and 1.0, respectively, to aid visualisation. The thin horizontal lines are drawn to indicate the baselines.

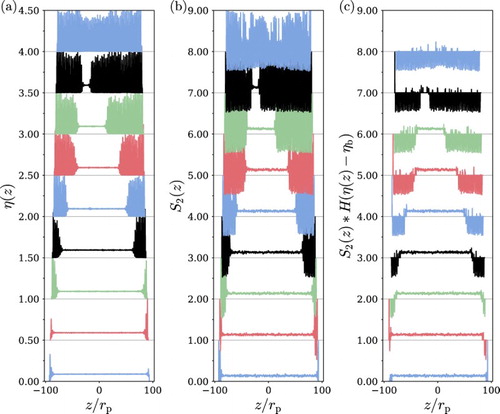
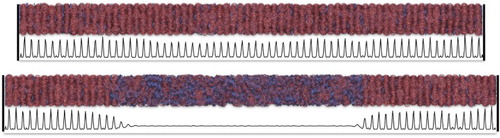
Figure 6. Representative configurations of systems comprising N=8000 nanorings in planar confinement with a transverse simulation box length of obtained by molecular-dynamics simulation. The longitudinal box lengths correspond to (bottom) and (top). Particles are shaded according to their orientations with respect to the planar wall. The corresponding packing fraction profiles are also shown in each snapshot to aid visualisation of the layers.

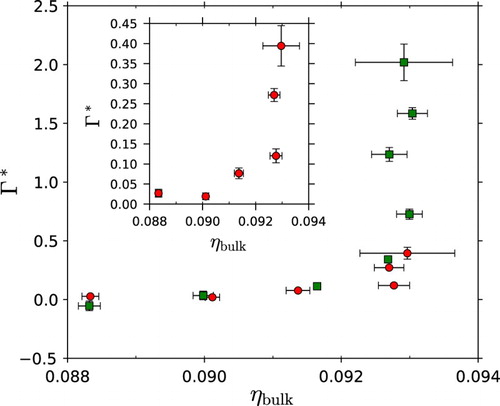
In a final analysis, we examine the surface adsorption of nanorings obtained from Equation (3(3) ) for both system sizes and the findings are shown in Figure 7. At low bulk packing fraction, the adsorption of the nanorings onto the surface is very small, which is consistent with the packing fraction profiles presented in Figures 4(a) and 5(a). As the bulk packing fraction is increased the adsorption of the particles increases with a sharp increment at the bulk isotopic–smectic transition. While the number of SmA layers formed below this bulk phase transition increases rapidly with the density of the system, the sharp increase of the surface adsorption near the transition suggests a first-order isotropic–smectic phase transition as previously reported for the bulk systems [81]. In order to assess the nature of the transition in more detail, more extensive simulations are required; this will be addressed in subsequent work.

Figure 7. Surface adsorption as a function of bulk packing fraction for systems of nanorings in planar confinement obtained by molecular-dynamics simulation. Only the states with densities below the bulk isotropic–smectic phase transition (η_iso = 0.101) are shown. The circles correspond to the values for a system comprising N=4000 particles and the squares to those comprising N=8000 particles. The results for the system of N=4000 particles is shown in more detail in the inset.

4. Conclusions

Nanoring systems in the bulk and under confinement are characterised by the formation of low-density layered liquid-crystalline states with large voids, referred to here as lacuna smectic phases. We have presented a computer simulation study of the phase behaviour and ordering of nanorings confined in planar slit pores with wall separations large enough to allow for the clear formation of surface and bulk regions. Near the planar wall, the nanorings tend to adsorb forming well-defined smectic layers in coexistence with an isotropic phase in the bulk region. The smectic layers exhibit unusual planar anchoring and anti-nematic orientational ordering as revealed by the negative values of the nematic order parameter. The spacing between the smectic layers is about twice the radius of the particles in agreement with the behaviour found for nanorings in the bulk. In contrast to what is typically found for confined liquid-crystalline systems involving convex particles, no apparent biaxiality is found for the nanorings in planar confinement. As the density of the system is increased, the bulk isotropic region exhibits a macroscopic phase transition to a smectic phase which is stable across the entire system. The isotropic–smectic phase transition is seen to occur at overall densities which are slightly below those reported for the bulk systems. While the growth of the smectic layers from the wall to the central region is of a continuous nature, an analysis of the surface adsorption suggests that the isotropic–smectic phase transition is first order in nature. Since the degree of biaxiality in the SmA phases is negligible at the densities studied (the system remains unaxial), ring-shaped mesogens are potential building blocks for templated structures with perfect anti-nematic surface ordering that could be used for optical applications.

Acknowledgments

We are delighted to dedicate this work to our inspirational friend and colleague Professor Daan Frenkel on the occasion of his 70th birthday. We thank the Computational Shared Facility of the University of Manchester for the computing time.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Carlos Avendano http://orcid.org/0000-0002-3157-7318

George Jackson   http://orcid.org/0000-0002-8029-8868

Additional information

Funding

GJ acknowledges funding to the Molecular Systems Engineering Group from the Engineering and Physical Sciences Research Council (EPSRC) of the UK (grants GR/T17595, GR/N35991, EP/E016340 and EP/J014958), the Joint Research Equipment Initiative (JREI) (GR/M94426), and the Royal Society-Wolfson Foundation refurbishment scheme.