The spectrum of the atomic orbital overlap matrix and the locality of the virtual electronic density matrix

Abstract

It is well known that near-linear dependencies in the atomic orbital (AO) basis will impede electronic-structure calculations since the inverse AO overlap matrix will be ill-defined. However, small eigenvalues will also impact the locality of the virtual density matrix. The virtual density matrix is relevant for developing efficient local approaches in electronic-structure theory, and recent literature shows that orthogonal molecular orbitals (MOs) are not optimal for exploiting locality. As size of molecules treated is increasing and high-quality basis sets are used, the problem is becoming more pronounced and challenges similar to those for extended systems appear. Here it is shown that the spectrum of the AO overlap matrix puts severe restrictions on the locality of the virtual density matrix, and that locality cannot be recovered by excluding components corresponding to near-singular eigenvalues. The effect is seen even when eigenvalues are orders of magnitude from being near-singular, and occurs also for small basis sets such as cc-pVDZ depending on the molecular system. Non-orthogonal orbitals do not constitute a solution to the problem, but they may be more convenient since lack of locality in the density matrix can be shifted from MO coefficients to the inverse MO overlap matrix.

GRAPHICAL ABSTRACT

Keywords:

• Orbital locality
• near-linear dependence
• non-orthogonal orbitals
• embedding approaches

1. Introduction

With todays powerful computers, electronic-structure methods are routinely being applied to larger and larger molecular systems employing high-quality atomic orbital (AO) basis sets. A high-quality AO basis is especially important when describing electron correlation or if molecular properties such as excitation energies, polarisabilites etc., are to be computed. For large molecular systems, local correlation approaches [1–5] and electronic-structure embedding theories [6–14] have been exceedingly popular approaches for extending the applicability range of accurate wave function models. These approaches exploit the locality of phyical interactions such as the dynamical electron correlation effects and locality of molecular properties. However, as larger three-dimensional systems and highly ordered extended systems are considered, increasing the size of the AO basis set will quickly introduce near-linear dependencies in the basis. Near-linear dependencies in the AO basis is characterised by eigenvalues of the AO overlap matrix which tend toward numerical zero, and is qualitatively different than the problem of exact linear dependencies, as pointed out by Löwdin and collaborators [15]. This is a well-known problem, discussed as early as in 1952 by Parmenter [16], and for molecular systems near-linear dependencies arise since AOs on different centers are non-orthogonal to each other. In particular, this is a pronounced issue for highly ordered three-dimensional extended systems, as discussed by both Löwdin [17,18] and by Aissing and Monkhorst [19]. Aside from the non-orthogonality of AOs, the problem is intensified by the fact that the AOs are developed and designed to describe atoms in free space and small molecular systems. Hence, when considering dense three-dimensional systems, there is an concerted effect from AOs on different centers which greatly enhances near-linear dependencies since the space is spanned much faster when expanding the basis set on multiple atomic centers than on a single atomic center.

Near-linear dependencies will impede calculations since numerical noise will be enhanced in the calculation. For a general calculation, a much-used and simple solution to the problem of near-linear dependencies is to carry out a canonical orthogonalisation of the AO overlap matrix followed by exclusion of components [15] with eigenvalues lower than a given threshold, typically around 10${}^{-6}$. This removes near-linear dependencies from the basis, without compromising the quality, and the calculation may be performed. This scheme can be justified by considering the analysis of Lykos and Schmeising [20], showing that the eigenvectors of the AO overlap matrix with the largest eigenvalues are so-called maximum overlap orbitals. I.e. orbitals generated by eigenvectors with small eigenvalues represents a small overlap with the AO basis, and hence excluding such eigenvectors does not deteriorate the quality of the basis set appreciably. However, which numerical value for threshold to use is rather arbitrary and the threshold is not a size-intensive measure. A more profound problem with near-linear dependencies arises when locality of orbital spaces are to be exploited. Near-linear dependencies in the AO basis will result in a non-local orthogonal molecular orbital (MO) space, as the occupied and virtual density matrices are connected via the inverse AO overlap. When eigenvalues of the AO overlap matrix are small, the inverse AO overlap will be non-local and hence the density matrices must reflect this non-locality. The occupied density matrix reflects the physics of the system and will only contain components necessary for this. The virtual density matrix, however, will contain the residual space and will have to abide by the behaviour of the inverse AO overlap matrix. Since the density matrix is a direct connection of orthogonal MO coefficients, the orthogonal MOs cannot be local if the density matrix is non-local. The eigenvalues of the AO overlap matrix will therefore dictate the extent of the orthogonalisation tails if localising MOs for such a density matrix. The non-locality is not a result of the occupied and virtual partitioning, and will also be seen for e.g. Löwdin symmetric orthogonalised AOs. The Löwdin symmetric orthogonalisation of the AOs is generated by the inverse square root of the AO overlap matrix, and it generates an orthogonal basis that in the least-square sense resembles the original AOs most [21]. They are usually considered to be local, but the locality of this basis depends directly on the locality of the inverse AO overlap matrix. A general discussion on how orthogonalisation impacts locality has previously been discussed [22], but not in terms of the dependence on the spectrum of the AO overlap matrix. For non-orthogonal MOs, the coefficients connect via the inverse of the MO overlap, and therefore local MO coefficient vectors may describe a non-local density matrix provided that the inverse of the MO overlap is non-local. Thus, the non-orthogonal orbitals are localisable even if orthogonal orbitals are not, although localisation of non-orthogonal orbitals require particular attention to the parametrisation [23]. A much-used set of non-orthogonal orbitals to span the virtual space is the set of projected atomic orbitals (PAOs). In addition to being non-orthogonal, it is a redundant and non-normalised set. Recent literature shows that PAOs are more suitable for local correlation methods (either directly [24] or as starting point for orbitals tailored for given occupied orbitals [25–27]) than localised orthogonal MOs [28,29]. Orthogonal MOs may have a highly localised main distribution [30], but if the space spanned by orthogonalisation tails of local MOs away from a given region is significant, they will not represent an efficient basis. This has been numerically shown by Hansen et al. [24] It should be noted that orbitals exploited for reduced orbital spaces need in principle not be local, but rather tailored for the property in question. Examples of this are the pair-natural orbitals [26,31] for the correlation problem and natural transition orbitals [32] and correlated natural transition orbitals [33,34] for vertical excitation energies. The success of these approaches lies in their specificity of generating suitable orbitals for the property in question rather than a general orbital space for a given region. These approaches will not be discussed here.

Despite a variety of discussions on the connection between eigenvalues of the AO overlap matrix and important quantities such as orbital energies and overlap with original AO basis [20,35], symmetry property of orbitals [35], and accuracy [36], a discussion on the connection to spatial locality is lacking. In this paper, the connection of the near-linear dependence of the AO basis and orbital space locality is discussed. The connection between the eigenvalues AO overlap matrix and the maximum achievable locality of an orthogonal orbital space is discussed from both a theoretical and numerical point of view. The discussion illustrates that the concerted effort of AOs has a far greater impact on the locality of resulting orbital spaces, than the locality of each individual AO in a given basis. The consequences of the AO basis set may in some cases be circumvented by the use of non-orthogonal redundant orbitals, such as PAOs, to space the virtual orbital space. However, the PAOs do not constitute a solution to the general underlying problem with the AO basis. Thus, for any extension in developments for the local approaches, e.g. for molecular properties, the problem of the underlying AO basis will present itself in new forms. For this, the paper offers no solutions. However, it does raise the question whether one also for large and dense molecular systems must take inspiration from literature on extended systems, where basis sets used have no small exponents due to the concerted effect of AOs.

The paper is organised as follows. In Section 2 an overview of the connection between the spectrum of the AO overlap matrix and density matrices is discussed, and in Section 3 the consequences of near-linear dependencies are characterised numerically and the effect of removing such components is illustrated and discussed. A summary and concluding remarks are given in Section 4.

2. Theory

In this Section, we review the connection between the spectrum of the AO overlap martrix and the occupied and virtual density matrices. The density matrices are then discussed in terms of orthogonal and non-orthogonal MOs.

2.1. The atomic orbital overlap matrix

The AO overlap matrix $\mathbf{S}$ is defined by the elements (1) $S_{\mu \nu }=⟨{\chi }_{\mu }|{\chi }_{\nu }⟩,$(1) where $\{{\chi }_{\tau }|\tau =1,2,\dots ,m\}$ is a collection of AOs centered on the different atomic centers in the molecule. The AOs have varying spatial extent depending on the AO basis set chosen and nuclear charge, but $\mathbf{S}$ will be a matrix local in space even for AO basis sets augmented with diffuse functions. Local in space here means that the elements $S_{\mu \nu }$ as a function of distance, $R_{\mu \nu }$, between the centers of the ${\chi }_{\mu }$ and ${\chi }_{\nu }$ displays a clear distance decay. We may carry out an eigenvalue decomposition of $\mathbf{S}$ to obtain the matrix of orthogonal eigenvectors, $\mathbf{U}=({\mathbf{u}}_1,{\mathbf{u}}_2,\dots ,{\mathbf{u}}_m)$, and the diagonal matrix of corresponding eigenvalues $\mathbf{\Lambda }$, (2) $\mathbf{S}=\mathbf{U}\mathbf{\Lambda }{\mathbf{U}}^{\text{T}},{\mathrm{\Lambda }}_{ij}={\lambda }_i{\delta }_{ij}.$(2) The inverse of $\mathbf{S}$ is given by (3) ${\mathbf{S}}^{-1}=\mathbf{U}{\mathbf{\Lambda }}^{-1}{\mathbf{U}}^{\text{T}}.$(3) When $\mathbf{S}$ is near singular, i.e. one or more eigenvalue are tending toward numerical zero, the inversion can be carried out by excluding eigenvectors ${\mathbf{u}}_i$ corresponding to ${\lambda }_i$ which are below some threshold (typically around ${10}^{-6}$). Whereas $\mathbf{S}$ always is local in space, the spatial locality of ${\mathbf{S}}^{-1}$ will be compromised by the magnitude of the inverse eigenvalues of $\mathbf{S}$. Removing components corresponding to eigenvalues larger than the threshold, e.g. on the order of 10${}^{-4}$, will compromise the basis set quality and further (for unchanged $\mathbf{S}$) destroy orthogonality of orbitals. One may consider removing components based on a minimal change in matrix norm such as Frobenius or $l_2$ norm. The norm of the change of $\mathbf{S}$ upon exclusion of eigenvalues will then be the square root of the sum of removed squared eigenvalues. Hence, one may use this approach to require a maximum norm of the change in $\mathbf{S}$ upon exclusion, but the dense spectrum of $\mathbf{S}$ will still pose a problem in terms of the balance between reducing the magnitude of ${\mathbf{S}}^{-1}$ and changing $\mathbf{S}$. Other approaches, such as rank-revealing QR factorisation may also be used. However, the diagonals of the upper right triangular matrix, $\mathbf{R}$, will not display a clear reduction in numerical rank. The diagonals of $\mathbf{R}$ will exhibit a structure similar to those of the eigenvalues of $\mathbf{S}$, namely a densely packed spectrum without an obvious cut-off. This is likely a consequence of the nature of the problem, i.e. that the problem only arises due to the concerted effect of AOs on many centers.

2.2. The connection to the molecular orbital space

Consider a set of occupied, ${\mathbf{C}}_{\text{o}}$, and virtual, ${\mathbf{C}}_{\text{v}}$, MO coefficients which may either be a set of start guess orbitals or a set of optimised Hartree–Fock orbitals. For orthogonal orbitals, the coefficients must satify, (4) ${\mathbf{C}}_{\text{o}}{\mathbf{C}}_{\text{o}}^{\text{T}}\mathbf{S}+{\mathbf{C}}_{\text{v}}{\mathbf{C}}_{\text{v}}^{\text{T}}\mathbf{S}\equiv {\mathbf{D}}_{\text{o}}\mathbf{S}+{\mathbf{D}}_{\text{v}}\mathbf{S}=\mathbf{1},$(4) where the definitions of the occupied density matrix, ${\mathbf{D}}_{\text{o}}$, and the virtual density matrix, ${\mathbf{D}}_{\text{v}}$, have been introduced. The occupied density matrix is responsible for describing the electronic density of the molecular system, and the virtual density matrix may be viewed as the residual space from the Hartree–Fock calculation. For post-Hartree–Fock models, the residual space will be crucial for accurate calculations. I.e. going from a small AO basis to a large AO basis will have a certain effect on the occupied density matrix, but the significant impact will be for the virtual density matrix. Further, since the occupied density matrix must describe the electronic density, its form and spatial locality with respect to distance decay will be governed by requirements of the molecular system. This is not the case for the virtual density matrix. The virtual density matrix will, due to Equation (4(4) ${\mathbf{C}}_{\text{o}}{\mathbf{C}}_{\text{o}}^{\text{T}}\mathbf{S}+{\mathbf{C}}_{\text{v}}{\mathbf{C}}_{\text{v}}^{\text{T}}\mathbf{S}\equiv {\mathbf{D}}_{\text{o}}\mathbf{S}+{\mathbf{D}}_{\text{v}}\mathbf{S}=\mathbf{1},$(4) ), be required to fulfill (5) ${\mathbf{D}}_{\text{v}}={\mathbf{S}}^{-1}-{\mathbf{D}}_{\text{o}}.$(5) Near-linear dependencies, as discussed in Section 2.1, will therefore have severe consequences for the spatial locality of the virtual density matrix. Orthogonal orbitals must directly reflect non-locality of a density matrix through (6) $[{\mathbf{D}}_{\text{v}}{]}_{\mu \nu }=\sum _a^{\text{virt}}{C}_{\mu a}{C}_{\nu a},$(6) where we have used the virtual density matrix as an example. Hence, if $[{\mathbf{D}}_{\text{v}}{]}_{\mu \nu }$ is large for ${\chi }_{\mu }$ and ${\chi }_{\nu }$ centered far from each other, there must be one or several virtual orbital coefficient vectors, ${\mathbf{C}}_a$, which have significant elements both for element $C_{\mu a}$ and $C_{\nu a}$.

For non-orthogonal molecular orbitals (but with occupied and virtual space orthogonal to each other), the density matrices are given by (7) $\begin{array}{r}{\mathbf{D}}_{\text{o}}={\mathbf{C}}_{\text{o}}({\mathbf{S}}_{\text{oo}}^{\text{mo}}{)}^{-1}{\mathbf{C}}_{\text{o}},\end{array}$(7) (8) $\begin{array}{r}{\mathbf{D}}_{\text{v}}={\mathbf{C}}_{\text{v}}({\mathbf{S}}_{\text{vv}}^{\text{mo}}{)}^{-1}{\mathbf{C}}_{\text{v}},\end{array}$(8) where ${\mathbf{S}}_{\text{oo}}^{\text{mo}}$ and ${\mathbf{S}}_{\text{vv}}^{\text{mo}}$ are the occupied-occupied and virtual-virtual blocks, respectively, of the MO overlap matrix ${\mathbf{S}}^{\text{mo}}={\mathbf{C}}^{\text{T}}\mathbf{S}\mathbf{C}$. For a non-orthogonal set, element $[{\mathbf{D}}_{\text{v}}{]}_{\mu \nu }$ is generated by two virtual orbitals coefficient vectors connected by the inverse MO overlap matrix, (9) $[{\mathbf{D}}_{\text{v}}{]}_{\mu \nu }=\sum _{ab}^{\text{virt}}{C}_{\mu a}({\mathbf{S}}_{\text{vv}}^{\text{mo}}{)}_{ab}^{-1}{C}_{\nu b}.$(9) Hence, some restrictions can move from the orbital coefficient vectors themselves to the inverse MO overlap matrix, when considering non-orthogonal MOs.

2.3. Physical significance of the eigenvalues of the AO overlap matrix

The eigenvectors of $\mathbf{S}$, $({\mathbf{u}}_1,{\mathbf{u}}_2,\dots ,{\mathbf{u}}_m)$, defines a new set of non-orthogonal orbitals, (10) ${\overline{\chi }}_i=\sum _{\mu }{\chi }_{\mu }{u}_{\mu i}.$(10) The projection of the function ${\overline{\chi }}_i$ with the original basis can be written as, (11) ${\omega }_i=\sum _{\mu }|⟨{\chi }_{\mu }|{\overline{\chi }}_i⟩{|}^2={\lambda }_i^2.$(11) Thus, the eigenvalues ${\lambda }_i$ are measures of the magnitude of overlap between the functions ${\overline{\chi }}_i$ and the original basis set. As noted by Lykos and Schmeising [20] the eigenvectors of $\mathbf{S}$ constitute what they call maximum overlap orbitals, i.e. orbitals which maximises the overlap with the original basis set. Excluding eigenorbitals with corresponding small eigenvalues therefore seems a reasonable approach at first glance. However, for larger molecules with AO basis sets of appreciable size, the spectrum of eigenvalues becomes dense with an increasing number of small eigenvalues. Excluding eigenorbitals based on a cut-off values for the eigenvalues of such that the magnitude of the inverse eigenvalues of $\mathbf{S}$ does not exceed the largest eigenvalues of $\mathbf{S}$, will have an impact on computed energy and properties.

3. Numerical illustrations

In this section we present numerical illustrations on the connection between the spectrum of $\mathbf{S}$ and maximum achievable locality in MO spaces. Three different molecular systems will be used for this purpose; eicosane (C${}_{20}$H${}_{42}$), a finite graphene-sheet (C${}_{106}$H${}_{28}$) and a finite slab of diamond (C${}_{331}$H${}_{216}$). The systems are chosen to see the concerted effect of AOs in one dimension, two dimensions and three dimensions, respectively. Since all three systems only contain carbon and hydrogen, the same AOs are involved for all three systems, i.e. the differences between systems will be due to geometric ordering of the AO centers. Due to Equation (5(5) ${\mathbf{D}}_{\text{v}}={\mathbf{S}}^{-1}-{\mathbf{D}}_{\text{o}}.$(5) ), we will use the decay properties of ${\mathbf{S}}^{-1}$ to illustrate requirements on ${\mathbf{D}}_{\text{v}}$. This to emphasise that the dominating effects with respect to locality (or lack thereof) for the virtual space is unrelated to the physical bonding situation of the molecule. Locality will be illustrated by plotting the distance decay of a matrix. The absolute value of the elements of a matrix, $|M_{\mu \nu }|$, are plotted as a function of the distance, $R_{\mu \nu }$, between atomic centers for AOs ${\chi }_{\mu }$ and ${\chi }_{\nu }$. For simplicity, only the maximum absolute element, $\text{max}|M_{\mu \nu }|$, will be plotted for a given distance $R_{\mu \nu }$.

3.1. The effect of near-dependencies on spatial locality

In Figure 1 the distance decay (as described above) of ${\mathbf{S}}^{-1}$ is shown for eicosane, graphene and diamond using basis sets cc-pVDZ, cc-pVTZ and cc-pVQZ. The smallest eigenvalue of $\mathbf{S}$ are tabulated in Table 1. First considering the cc-pVDZ results, it is seen that the curves for all three molecules display a decay behavior, where max$|S_{\mu \nu }^{-1}|$ is reduced several orders of magnitude from $R_{\mu \nu }=2$ Å to $R_{\mu \nu }=12$ Å. However, the curve for diamond (squares) starts at higher numerical values than the curve for eicosane (circles), whereas the curve for graphene (triangles) at even higher numerical values than both diamond and eicosane. As seen from Table 1 graphene has the smallest ${\lambda }_{\text{min}}$ for cc-pVDZ. For the highly ordered and planar graphene structure, rather small eigenvalues of $\mathbf{S}$ are already encountered with cc-pVDZ. For cc-pVTZ, we see from Table 1 that the smallest eigenvalues of graphene and diamond are of the same order of magnitude ($6.32\times {10}^{-7}$ and 4.05$\times {10}^{-7}$, respectively), and they are several orders of magnitude lower than for eicosane (${\lambda }_{\text{min}}=1.55\times {10}^{-4}$). Looking at Figure 1 for cc-pVTZ (middle plot) it is seen that the curves for graphene (triangles) and diamond (squares) both start at $\text{max}|S_{\mu \nu }^{-1}|\approx {10}^5$ for $R_{\mu \nu }=2$ Å, whereas the curve for eicosane (circles) starts at $\text{max}|S_{\mu \nu }^{-1}|\approx {10}^3$ for $R_{\mu \nu }=2$ Å. For cc-pVQZ (Figure 1, right plot) the curve for diamond (squares) can barely be seen due to huge numerical values of $\text{max}|S_{\mu \nu }^{-1}|$, whereas the graphene curve (triangles) is within the plot but display large numerical values of $\text{max}|S_{\mu \nu }^{-1}|$. For cc-pVQZ, ${\lambda }_{\text{min}}$ for graphene and diamond are $5.97\times {10}^{-8}$ and $7.17\times {10}^{-10}$, respectively. For cc-pVQZ the eicosane curve (circles) has shifted upwards relative to cc-pVDZ and cc-pVTZ. Note that for cc-pVQZ ${\lambda }_{\text{min}}$ for graphene and diamond indicates that near-linear dependencies should be removed to avoid numerical issues in the calculation.

Figure 1. The distance decay of ${\mathbf{S}}^{-1}$ is plotted for eicosane (circles), graphene (triangles) and diamond (squares) for cc-pVDZ (left), cc-pVTZ (middle) and cc-pVQZ (right).

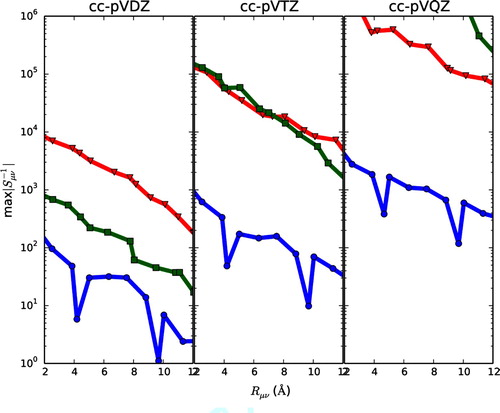
Table 1. The smallest eigenvalue og the AO overlap matrix (${\lambda }_{\text{min}}$) and the number of eigenvalues below ${10}^{-3}$ (N${}_{<}$) for the combination of molecules and basis sets discussed.

molecule (basis)	${\lambda }_{\text{min}}$	N${}_{<}$
eicosane (cc-pVDZ)	8.91$\times {10}^{-4}$	2
graphene (cc-pVDZ)	6.78$\times {10}^{-6}$	89
diamond (cc-pVDZ)	6.23$\times {10}^{-5}$	289
eicosane (cc-pVTZ)	1.55$\times {10}^{-4}$	19
graphene (cc-pVTZ)	6.32$\times {10}^{-7}$	206
diamond (cc-pVTZ)	4.05$\times {10}^{-7}$	974
eicosane (cc-pVQZ)	3.23$\times {10}^{-5}$	118
graphene (cc-pVQZ)	5.97$\times {10}^{-8}$	579
diamond (cc-pVQZ)	7.17$\times {10}^{-10}$	2937

All three systems consist solely of carbon and hydrogens, and the results for each basis set therefore illustrates the effect on locality due to the concerted effect of the geometrical arrangement of centers of basis functions rather than the effect of the locality of single AOs. Further, the results show a cross-over where the least favorable system (in terms of locality of ${\mathbf{S}}^{-1}$) shifts from being the highly-ordered planar graphene for cc-pVDZ to the three-dimensional diamond structure for cc-pVQZ. For cc-pVTZ the results for graphene and diamond are similar. Thus, the nature of the bonding (non-local conjugated versus localised covalent bonding) is irrelevant for the effects of locality on the virtual MO space as dictated by ${\mathbf{S}}^{-1}$ (through Equation (5(5) ${\mathbf{D}}_{\text{v}}={\mathbf{S}}^{-1}-{\mathbf{D}}_{\text{o}}.$(5) )), as the nature of ${\mathbf{S}}^{-1}$ is dominating. This further explains some of the misinterpretations of poor virtual locality of orbital spaces of conjugated systems. Due to their planarity, the locality of the virtual space will be more prone to effects of eigenvalues of ${\mathbf{S}}^{-1}$ than non-planar molecules in addition to being affected by the less local nature of ${\mathbf{D}}_{\text{o}}$. However, the effect of ${\mathbf{S}}^{-1}$ will dominate over ${\mathbf{D}}_{\text{o}}$ due to the large norm of ${\mathbf{S}}^{-1}$. Note that it is the locality of the virtual density matrix which display decay behaviour as ${\mathbf{S}}^{-1}$, it will therefore be impossible for an orbital localisation scheme to recover locality, as the density matrix is invariant with respect to orthogonal transformations among the orbitals.

3.2. Removing near-dependencies by canonical orthogonalisation

Here we look at the effect of removing components of the basis which corresponds to eigenvalues of $\mathbf{S}$ below a given threshold. Although a common threshold to use is usually on the order of ${10}^{-6}$, here we use an threshold of ${10}^{-3}$. The threshold is chosen so that $\frac{1}{{\lambda }_{\text{min}}}$ is on the same order of magnitude as ${\lambda }_{\text{max}}$. Hence, all eigenvalues contributing to the large norm of ${\mathbf{S}}^{-1}$ is removed to see whether this recovers locality. In a practical calculation, a threshold of this order of magnitude would compromise the basis set and also destroy idempotency relations of the density matrices over the unchanged $\mathbf{S}$. In Figure 2 the distance decay of ${\mathbf{S}}^{-1}$ after removing components for ${\lambda }_i<{10}^{-3}$ are plotted for eicosane (circles), graphene (triangles) and diamond (squares) for cc-pVDZ (left), cc-pVTZ (middle) and cc-pVQZ (right). For ease of comparison, Figure 2 is plotted on the same scale as Figure 1. The number of removed components, $N_{<}$, are listed in Table 1.

Figure 2. The distance decay of ${\mathbf{S}}^{-1}$ is plotted for eicosane (circles), graphene (triangles) and diamond (squares) for cc-pVDZ (left), cc-pVTZ (middle) and cc-pVQZ (right). For the presented calculations, a canonical orthogonalisation of the basis was carried out, and all components corresponding to eigenvalues smaller than ${10}^{-3}$ were removed. See Table 1 for how many components are removed in each case.

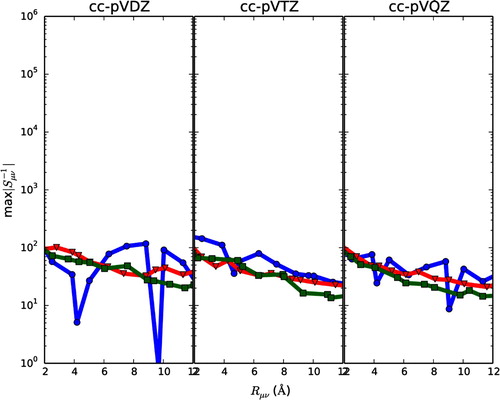
Comparing Figure 2 to 1 it is seen that removing components for small ${\lambda }_i$ greatly reduces the numerical values of $\text{max}|S_{\mu \nu }^{-1}|$, as expected from Equation (3(3) ${\mathbf{S}}^{-1}=\mathbf{U}{\mathbf{\Lambda }}^{-1}{\mathbf{U}}^{\text{T}}.$(3) ). As an example, $\text{max}|S_{\mu \nu }^{-1}|$ at $R_{\mu \nu }=2$ Å is reduced from $\approx {10}^6$ for graphene (cc-pVQZ) to $\approx {10}^2$. Further, the $\text{max}|S_{\mu \nu }^{-1}|$ values for all three molecular systems are seen to be of similar order of magnitude. However, there is only a weak decay behaviour. From 2 Å to 12 Å, $\text{max}|S_{\mu \nu }^{-1}|$ has not decayed by one whole order of magnitude. For comparison, the distance decay of $\mathbf{S}$ for cc-pVQZ is plotted in Figure 3 (note the different scales of the axis). This implies that although the huge norm of ${\mathbf{S}}^{-1}$ has been reduced, it will be impossible to properly localise molecular orbitals since they must fulfill the tail behaviour (behaviour at long $R_{\mu \nu }$) of ${\mathbf{D}}_{\text{v}}$, as dictated by ${\mathbf{S}}^{-1}$.

Figure 3. The distance decay of $\mathbf{S}$ for eicosane using cc-pVQZ.

3.3. Non-orthogonal sets of orbitals

The previous section illustrates that orthogonality has severe consequences for locality of the virtual orbital space, especially when considering highly ordered systems and/or large basis sets. Thus, one may turn to non-orthogonal orbitals as they need not describe the non-locality of the density matrix themselves (see Section 2.2). In this section, we present numerical illustrations for a commonly used set of non-orthogonal orbitals, the PAOs. The PAOs constitute a non-orthogonal and redundant set of orbitals. It is therefore of interest to see how the sets of PAOs behave for one-, two-, and three-dimensional systems as one increase the size of the basis set. In this section, we consider the normalised PAOs (excluding core orbitals). In Figure 4 the distance decay of normalised orbital coefficients, ${\mathbf{C}}^{\text{pao}}=\mathbf{1}-{\mathbf{D}}_{\text{o}}\mathbf{S}$, for PAOs is plotted. Note the difference in scale on the y-axis compared to Figure 1. From Figure 4 (left) it is seen that for cc-pVDZ it is the curve for graphene (red triangles) that stands out. Since the orbital norms need not reflect ${\mathbf{S}}^{-1}$, the effect of a non-local structure ${\mathbf{D}}_{\text{o}}$ can be seen for graphene using cc-pVDZ. Looking at the results for cc-pVTZ (Figure 4, middle) it is seen that the effects of the underlying AO basis is increasing, as is mainly seen for diamond (squares) which is three-dimensional. At this point PAOs for graphene and diamond exhibit similar distance decays. For cc-pVQZ (Figure 4, right) the curve for diamond (squares) is above the one for graphene (triangles). For all three basis sets the behaviour of the curves for eicosane (circles) are similar.

Figure 4. The distance decay of ${\mathbf{C}}^{\text{pao}}$ is plotted for eicosane (circles), graphene (triangles) and diamond (squares) for cc-pVDZ (left), cc-pVTZ (middle) and cc-pVQZ (right).

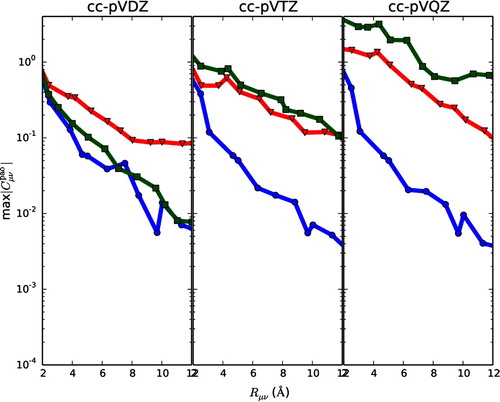
Although Figure 4 is not directly comparable to Figure 1 since here the coefficients are investigated (whereas it was the virtual density matrix through ${\mathbf{S}}^{-1}$ in Figure 1), the same trends are seen in the two figures with respect to the effect on ordered two- and three-dimensional systems when the basis set is increased. The problems are, however, less pronounced for the PAOs than it is for orthogonal orbitals. Hence, using non-orthogonal orbitals ${\mathbf{S}}^{-1}$ will be less detrimental to the calculation, but not avoided.

4. Summary and concluding remarks

In this paper, the connection between the spectrum of the AO overlap matrix and locality of density matrices is discussed. The challenges arising due to the spectrum of the AO overlap matrix is increasingly relevant as developments in electronic-structure theory pushes the limits for the size of molecular systems and quality of basis sets used. The problem arises due to the use of a non-orthogonal AO basis as well as the fact that basis sets used for large molecular systems are developed and designed for single atoms and small molecular systems. For large molecules, there is an concerted effect of AOs, similar to that seen for extended systems. It is shown that when eigenvalues of the AO overlap matrix becomes small (but far from near-singular) the locality of the virtual density matrix will be severely impaired. The effect is seen already for small basis sets such as cc-pVDZ. The locality cannot be recovered by removing components corresponding to small eigenvalues, and a consequence is that orthogonal MOs is not a suitable basis to exploit locality. The presented results explain why localised molecular orbitals have been shown to perform poorly in terms of e.g. compact descriptions of electron correlation effects. The delocalisation effects through orthogonalisation affects compactness of representation. The orthogonalisation tails of the orthogonal MOs will be significant, even for small basis sets. Non-orthogonal sets of orbitals will display better distance decay, as the non-locality of the density matrices may be contained in the inverse MO overlap rather than in the molecular orbital coefficients themselves. However, some of the same trends seen for orthogonal orbitals are also seen for non-orthogonal sets such as the PAOs, although to a less extent. Non-orthogonality of orbitals may reduce the consequences, but it does not fix the underlying problem of the AO basis.

Acknowledgments

The author acknowledges financial support from the Norwegian Research Council through project no. 275506, and computations were performed on resources provided by UNINETT Sigma2 – the National Infrastructure for High Perfromance Computing and Data Storage in Norway.

Disclosure statement

No potential conflict of interest was reported by the author.

Additional information

Funding

The author acknowledges financial support from the Norwegian Research Council through project no. 275506, and computations were performed on resources provided by UNINETT Sigma2 – the National Infrastructure for High Performance Computing and Data Storage in Norway.