Beyond the helium buffer: ¹²C⁻₂ rotational cooling in cold traps with H₂ as a partner gas: interaction forces and quantum dynamics

Abstract

The scattering cross-sections and corresponding rate coefficients for rotationally inelastic collisions of ${}^{12}$C${}_2^{-}$ (${}^2{\mathrm{\Sigma }}_g^{+}$) with H${}_2$ (${}^1{\mathrm{\Sigma }}_g^{+}$) are presented over a broad range of cold-trap temperatures. They have been calculated using quantum scattering theory that employs a new ab initio potential energy surface. The rate coefficients for the inelastic processes in the anionic partner are used to model the thermalisation dynamics of ${}^{12}$C${}_2^{-}$ using H${}_2$ as a buffer gas, a trap partner which is found here to be far more efficient than the typical buffer gas He and even more so than when using Ar as a partner gas. The microscopic physics underlying these findings is discussed in some detail. We additionally compute and discuss ${}^{12}$C${}_2^{-}$ quadrupole transitions by spontaneous emission and use the newly computed rates to show that the anion's rotational levels should be in local thermal equilibrium at typical interstellar conditions.

GRAPHICAL ABSTRACT

Keywords:

• Inelastic collisions
• molecular anions
• rate constants
• buffer gas cooling
• quadrupole transitions

1. Introduction

The diatomic carbon anion, C${}_2^{-}$ has been described as ‘clearly the most studied system’ [1] in terms of molecular anions and indeed, its properties have been investigated both experimentally [2–17] and theoretically [18–27] for decades. Unusual for a molecular anion, C${}_2^{-}$ has bound electronically excited states [22] which is a consequence of the high electron affinity of neutral C${}_2$ of around 3.3 eV [6,10] in combination with the open shell character of the electronic configuration of carbon dimers. This has lead to C${}_2^{-}$ being proposed as a candidate for the first laser cooled molecular anion. The anion's $A^2{\mathrm{\Pi }}_u$ and $B^2{\mathrm{\Sigma }}_u^{+}$ electronic states have large Franck-Condon overlap factors with the $X^2{\mathrm{\Sigma }}_g^{+}$ ground state for transitions between their lowest vibrational levels [25,28]. Simulations of laser cooling using the $B^2{\mathrm{\Sigma }}_u^{+}$ [1] and $A^2{\mathrm{\Pi }}_u$ [29] states suggests that C${}_2^{-}$ can, in principle, be cooled efficiently to milikelvin temperatures using Doppler or Sisyphus cooling in Paul or Penning traps and that photodetachment could access even lower temperatures [30]. If laser cooling of C${}_2^{-}$ anions were to be realised, it would open up the possibility of sympathetically cooling other anions [29] or even antiprotons [30].

In a series of recent works, we have investigated various inelastic processes of noble gas atoms colliding with C${}_2^{-}$ to assess their usefulness as buffer gases for cold-ion trapping experiments. Our simulations showed that thermalisation times of the rotational states of C${}_2^{-}$ with noble gases decreased in the order helium > neon > argon, due to the increasing interaction energy with atomic size and with dipole polarisability which are then yielding larger rate coefficients [31,32]. We have also calculated the rate coefficients for vibrationally inelastic collisional quenching of the anion's $\nu =2$ and $\nu =1$ levels [33], a step which can be useful in laser cooling experiments. As C${}_2^{-}$ has no oscillating dipole, the vibrational levels are long lived with the ground electronic state's v = 2 levels persisting for over five seconds [13]. Collisions are thus the only viable means of directly quenching these states efficiently (another approach being to excite the molecule to a higher energy electronic state which can then spontaneously decay to lower vibrational levels in an allowed transition [17]). It was found that while rate constants for vibrational quenching with helium and neon were very low, argon provided far larger rates, again as a result of the much stronger interaction with the anion.

Although argon has relatively large rate coefficients for both rotationally and vibrationally inelastic collisions with C${}_2^{-}$, its use as a buffer gas is limited to temperatures above about 50 K as it freezes out at lower T values. This compares to He which can be used to reach far lower temperatures justifying its wide use as a buffer gas. Another possibility is to use hydrogen gas, H${}_2$, which has been used more often than argon and which is the focus of the present computational work. For the similar anion, CN${}^{-}$, we had found earlier that the rotationally inelastic rate coefficients for collisions with H${}_2$ were even larger than those for argon, leading to fast thermalisation times [34], thereby suggesting H${}_2$ may also be suitable as an efficient buffer gas for C${}_2^{-}$. Hydrogen gas has the advantage of being usable down to about 10 K before freezing out. On the other hand, hydrogen gas usually has the disadvantage of being a somewhat reactive species compared to noble gases. However, earlier experimental studies had found that C${}_2^{-}$ is essentially non reactive with H${}_2$ at room temperature [16,35], showing only limited reactivity even down to 12 K [16]. These findings, therefore, suggest that it is indeed worth considering H${}_2$ as an alternative buffer gas for C${}_2^{-}$ in relation to the more common choice of He gas. Hence, in the present work, the rate coefficients for rotationally inelastic collisions between C${}_2^{-}$ in its ground $X^2{\mathrm{\Sigma }}_g^{+}$ electronic state and H${}_2$ as a trap partner are obtained from a first principle study and analysed in terms of their behaviour under cold-ion trap conditions. We expect that the present investigation will serve as a complement to further studies of the collisionally inelastic rate coefficients for the vibrational quenching of the same partner anion with the same buffer gas that we shall be considering in a separate, future investigation.

The interaction of C${}_2^{-}$ with molecular hydrogen, the most abundant molecule in the universe, may also be of importance in astronomical environments where it has been suggested that C${}_2^{-}$ could be present as neutral C${}_2$ is abundant in interstellar space [36], comet tails [37] and is a common component of carbon stars [38,39]. The large electron affinity of C${}_2$ and strong electronic absorption bands of C${}_2^{-}$ [5] suggests that the anion could also be detected in space [40] but as yet no conclusive evidence of its presence has been found [41–43]. As the most abundant isotopologue ${}^{12}$C${}_2^{-}$ is a homonuclear diatomic molecule, it does not exhibit a pure ro-vibrational spectrum making its detection in emission difficult but transitions to and from low-lying excited electronic states may allow for the anions detection. The rotationally inelastic collisions considered here between C${}_2^{-}$ and H${}_2$ serve as a complement to our earlier work on C${}_2^{-}$/He collisions, the latter partner gas being the second most abundant gas in astronomical environments [31].

This work is organised as follows. In Section 2, the full ab initio quantum chemistry calculations are described along with the 4D potential energy surface (PES). The latter is then reduced to a 2D approximation for which an analytical form is obtained. Section 3 describes the details of the quantum scattering calculations used to investigate the rotational state-changing processes involving only the molecular anion in collision with the H${}_2$ partner. Rotationally inelastic cross-sections and rate coefficients are presented in Section 4 and further compared to other collision partners and systems. Kinetic modelling of the thermalisation process is presented in Section 5. A discussion of C${}_2^{-}$ quadrupole transitions and how this relates to critical densities is given in Section 6. Conclusions are drawn in Section 7.

2. C${}_2^{-}$/H${}_2$ Ab initio calculations & potential energy surface

The interaction energies between C${}_2^{-}$ (${}^2{\mathrm{\Sigma }}_g^{+}$) and H${}_2$ (${}^1{\mathrm{\Sigma }}_g^{+}$) were calculated ab initio with both molecules treated as rigid rotors. Bond lengths were held fixed at their equilibrium values of 1.269 Å for C${}_2^{-}$ [25] and 0.741 Å for H${}_2$ ( 1Å= 100 pm). Energies were calculated using the CCSD-T method for open shell systems [44,45] as implemented in MOLPRO [46,47] using the aug-cc-pV5Z basis set [48,49] centred on both the carbon and hydrogen nuclei of the partner molecules. The basis-set-superposition-error (BSSE) was also accounted for at all calculated points using the counterpoise procedure [50].

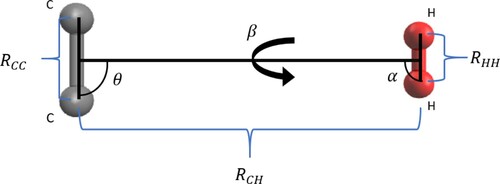
The tetra-atomic C${}_2^{-}$/H${}_2$ system is characterised by six degrees of freedom in the body-fixed frame which is reduced to four when both molecules bond lengths are fixed. The system is then spatially defined by the knowledge of three angles: θ, α, β and of $R_{CH}$, the distance between the C${}_2^{-}$ and H${}_2$ centres of masses as shown in Figure 1. The θ and α angles are polar angles with respect to $R_{CH}$ while β is the dihedral angle. Energies were calculated for three specific orientations of the H${}_2$ molecule: ‘perpendicular’ (α = 90 ${}^{\circ }$, β = 0${}^{\circ }$ ), ‘in-line’ (α = 0${}^{\circ }$, β = 0${}^{\circ }$) and ‘out-of-plane’ (α = ${90}^{\circ }$, β = 90${}^{\circ }$). For each of these orientations, energies were calculated on grids of $R_{CH}$, for 40 points between 2.6 and 25 Å, and θ between 0 and 90${}^{\circ }$ in 10${}^{\circ }$ intervals. The radial grid included a higher density of points around the minima regions at each selected angle. For some small values of $R_{CH}$ at small angles θ, where the potential is repulsive, some calculations did not converge. Energies for these geometries were obtained by fitting to an exponential function for each angular cut and extrapolating to small $R_{CH}$. Figure 2 shows energy diagrams of the three H${}_2$ orientations used, presenting various cuts of the PES for different values of θ polar angle. The ‘out-of-plane’ H${}_2$ orientation gives the least attractive interaction with the C${}_2^{-}$ anion, along with the $\theta =0$ and 90${}^{\circ }$ ‘perpendicular’ geometries. The most attractive region of the PES is given by the ‘in-line’ H${}_2$ orientation and for the polar angle $\theta ={90}^{\circ }$.

Figure 1. Definition of the body-fixed coordinates system.

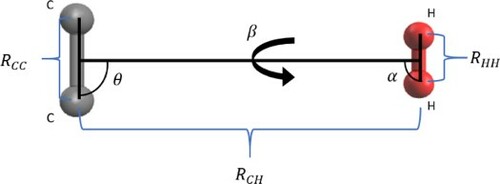
Figure 2. Cuts of C${}_2^{-}$/H${}_2$ PES along the radial coordinate $R_{CH}$ for the three H${}_2$ orientations used in the present calculations, plus its average value. Different different values of θ are shown.

To direct the quantum scattering calculations to investigate only the rotationally inelastic processes involving the C${}_2^{-}$ anionic partner, the initially computed four dimensional PES is reduced to a two dimensional PES by taking the average value of the interactions pertaining to the three H${}_2$ orientations described before: (1) $\begin{array}{rl}{V}_{av}(R,\theta )& =\frac{1}{3}(V_{perp}(R_{CH},\theta )+V_{in-line}(R_{CH},\theta )\\ & +V_{oop}(R_{CH},\theta )).\end{array}$(1) This 4D to 2D reduction of the PES is physically equivalent to restricting the H${}_2$ molecule to be only the para-hydrogen in its j = 0 level and has been already used in the past for various other systems [51–54]. For the temperatures of interest in this work (T $\le$ 100 K), the probability of exciting the H${}_2$ molecule is low as the energy spacing between the j = 0 and j = 2 levels of para-hydrogen is around 500 K [51]. This approximation has been checked for its accuracy: for SiS/H${}_2$ collisions a 4D vs 2D treatment only resulted in differences of around 10 % in the scattering cross-sections [52] and for HNC/H${}_2$ collisions the approximate treatment resulted in cross-sections within a factor of two of the 4D treatment while rates differed by less than 30 % [53]. Thus, despite the great simplification introduced for the quantum scattering treatment, which basically allows the same methods employed for the atom-rigid rotor scattering to be used for the present four-atom system, the cross-sections and in particular the rate coefficients are expected to remain reasonably accurate and to be of realistic values for our following discussion of the results.

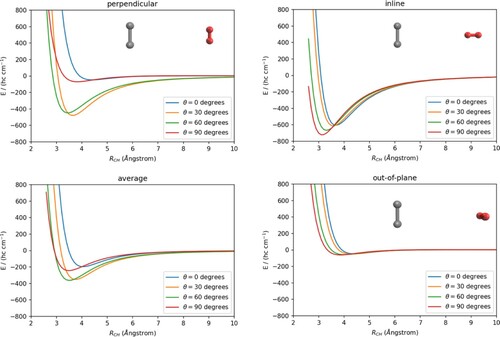
The C${}_2^{-}$-H${}_2$ averaged, 2D PES is shown in the left panel of Figure 3. The specific features of this reduced-dimensionality PES are clearly due to the averaging procedure and can be explained by comparing the present findings with those shown in the previous panels of Figure 2. For the ‘in-line’ H${}_2$ orientation, the interaction energy is at a minimum value for $\theta ={90}^{\circ }$ and decreases on moving to linear geometries, while for the ‘perpendicular’ orientation the minimum energy geometry occurs for $\theta ={30}^{\circ }$ and, as for the ‘out-of-plane’ geometries, only shallow minima occur at their respective perpendicular geometries with $\theta ={90}^{\circ }$. The present averaging procedure therefore results in the most attractive part of the 2D PES occurring for relative configurations which are off the perpendicular geometries. The global minimum of the interaction energy for the averaged 2D-PES is around $-400$ cm${}^{-1}$ at R = 3.6 Å and $\theta ={40}^{\circ }$. We can also see that the 2D-averaged C${}_2^{-}$/H${}_2$ PES is comparable to the full-dimension 2D C${}_2^{-}$/Ar PES which is shown in the right panel of Figure 3. For this atom-diatomic system, the minimum energy is −488 cm${}^{-1}$ at 3.7 Å and $\theta ={90}^{\circ }$. We, therefore, see that, on the whole, the C${}_2^{-}$/H${}_2$ PES remains attractive up to smaller distances than those occurring for the C${}_2^{-}$/Ar system, which becomes repulsive at larger distances (compare the 900 cm${}^{-1}$ contours shown for both plots). On the other hand, the C${}_2^{-}$/Ar interaction remains more strongly attractive to larger distances than those found for the 2D-C${}_2^{-}$/H${}_2$ system. This feature is due to the larger dipole polarisability of Ar of 11.070 $a_0^3$ [55], to be compared to that for H${}_2$ of 5.314 $a_0^3$ [56].

Figure 3. Contour plots of C${}_2^{-}$-H${}_2$ averaged 2D-PES (left) and full 2D-PES for the C${}_2^{-}$-Ar(right).The levels of energy contours are given in units of (hc cm${}^{-1}$).

The averaged C${}_2^{-}$/H${}_2$ 2D-PES was analytically represented by expanding it using a standard Legendre polynomial series as (2) $V_{av}(R,\theta )=\sum _{\lambda }^{{\lambda }_{max}}{V}_{\lambda }(R)P_{\lambda }(\cos \theta )$(2) where, because C${}_2^{-}$ is a homonuclear target and thus symmetric around $\theta ={90}^{\circ }$, only even terms of the Legendre series are required with integer label λ. Using a nine term expansion, i.e. with ${\lambda }_{\max }=16$, gave a root-mean-square error to the ab initio data of 1.8 cm${}^{-1}$ for geometries with potential energies below 1000 cm${}^{-1}$.

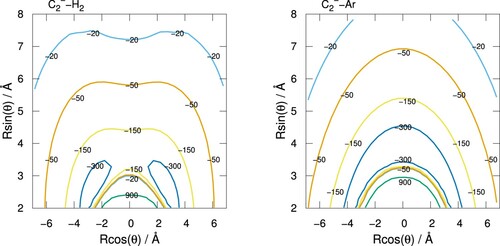
The radial coefficients $V_{\lambda }(r_{\mathrm{eq}}|R)$ for the most important terms in the expansion, i.e. for $\lambda =0,2$ and 4, are plotted in Figure 4 for C${}_2^{-}$ interacting with both H${}_2$ and Ar. For both systems, the spherical term $V_0$ has the largest magnitude and is responsible for the overall attraction of both systems. As expected from the preceding discussion, the interaction of C${}_2^{-}$ with Ar gives a more attractive $V_0$ term but for H${}_2$ this term is still relatively large in comparison to He and Ne shown in our earlier work [32]. In contrast, the $V_2$ term which is responsible for $\mathrm{\Delta }N=\pm 2$ transitions during collisions, has a deeper minimum for C${}_2^{-}$ interacting with H${}_2$ compared to Ar. This is a consequence of the averaged C${}_2^{-}$/H${}_2$ PES having a larger anisotropy than the C${}_2^{-}$/Ar PES as seen in Figure 3, with the off-perpendicular attractive wells of the former being the main contributors to this anisotropic feature. This suggests that the scattering cross-sections for $\mathrm{\Delta }N=\pm 2$ for C${}_2^{-}$/H${}_2$ collisions are expected to be larger than those for C${}_2^{-}$/Ar, which is indeed the case in the scattering calculations discussed below. The $V_4$ terms for both systems are similar in strength and are both repulsive for all R, this being slightly more so for the case of the H${}_2$.

Figure 4. Radial coefficients of the expansion given by Equation (2(2) $V_{av}(R,\theta )=\sum _{\lambda }^{{\lambda }_{max}}{V}_{\lambda }(R)P_{\lambda }(\cos \theta )$(2) ) for C${}_2^{-}$ interacting with H${}_2$ (solid lines) and Ar (dashed lines). Only the first three, most important radial functions are shown.

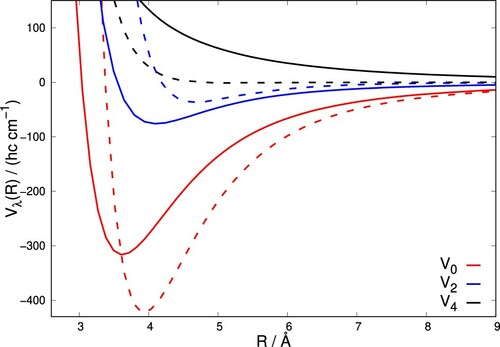
It is also significant to note that while the PESs and corresponding Legendre expansion coefficients for the C${}_2^{-}$/H${}_2$ and C${}_2^{-}$/Ar systems discussed here show a relatively strong interaction, far larger than C${}_2^{-}$/He for example, the interactions of the same anion with the open-shell, highly polarisable atoms like Li and Rb have a much stronger interactions. For these systems, the global minima of their corresponding PESs occur at perpendicular (T-shaped) atom-molecule geometries and are around $-18,000$ for C${}_2^{-}$/Li and $-10,500$ cm${}^{-1}$ for C${}_2^{-}$/Rb with corresponding $V_0$ term minima of around 12,000 (1.5 eV) and 8000 cm${}^{-1}$ (1.0 eV) respectively [26].

The expansion parameters $V_{\lambda }(R)$ for the averaged 2D C${}_2^{-}$/H${}_2$ PES are provided in the supplementary information as well as Fortran subroutines which give potential energies as a function of Jacobi coordinates.

3. Quantum scattering calculations

The quantum scattering calculations for the collision of C${}_2^{-}$ with para-H${}_2$(j = 0) are focused on the collisions causing rotational state-changing in the anionic partner, hence they are using the averaged 2D-PES discussed in the previous Section. They were carried out by employing our in-house quantum scattering code ASPIN [57] with the molecular anion treated as a rigid rotor (RR). The ground electronic state of C${}_2^{-}$ is ${}^2{\mathrm{\Sigma }}_g^{+}$, a doublet state. The presence of the electronic spin in a doublet state splits the usual nuclear rotational levels N of a rotating molecule into doublets so that each resultant rotational level j (other than the ground j = 0.5) is split into two values with $j=N\pm 0.5$. The energy of the rotational levels are given as (3) ${ϵ}_{jN}=\{\begin{array}{ll}{\displaystyle BN(N+1)+{\displaystyle \frac{1}{2}}\gamma N}& j=N+{\displaystyle \frac{1}{2}}\\ {\displaystyle BN(N+1)-{\displaystyle \frac{1}{2}}\gamma (N+1)}& j=N-{\displaystyle \frac{1}{2}}\end{array}$(3) where B is the rotational constant taken as 1.7438 cm${}^{-1}$ [25] and γ is the spin-rotation constant with a measured value of 4.25$\times {10}^{-3}$ cm${}^{-1}$ [9].

ASPIN makes use of the Coupled-Channel (CC) method to solve the Schödinger equation for scattering of an atom with a diatomic molecule. The method has been described in detail previously [57,58] and only a brief summary will be given here. For a given total angular momentum $\mathbf{J}\mathbf{=}\mathbf{l}\mathbf{+}\mathbf{j}$, the scattering wavefunction is expanded as (4) ${\mathrm{\Psi }}^{JM}(R,\mathrm{\Theta })=\frac{1}{R}\sum _{j,l}{f}_{lj}^J(R){\mathcal{Y}}_{jl}^{JM}(\hat{\mathbf{R}},\hat{\mathbf{r}})$(4) where l and j are the orbital and rotational angular momentum respectively, ${\mathcal{Y}}_{jl}^{JM}(\hat{\mathbf{R}},\hat{\mathbf{r}})$ are coupled-spherical harmonics for l and j which are eigenfunctions of J. The values of l and j are constrained, via Clebsch-Gordan coefficients, such that their resultant summation is compatible with the total angular momentum J [57,58]. $f_{lj}^J(R)$ are the radial expansion functions which need to be determined by numerical propagation. Substituting the expansion into the Schödinger equation with the Hamiltonian for atom-diatom scattering [57,58] leads to the CC equations for each value of J (5) $(\frac{{\mathrm{d}}^2}{\mathrm{d}{R}^2}+{\mathbf{K}}^2-\mathbf{V}-\frac{{\mathbf{l}}^2}{R^2}){\mathbf{f}}^J=0.$(5) Here each element of $\mathbf{K}={\delta }_{i,j}2\mu (E-{ϵ}_i)$ (where ${ϵ}_i$ is the channel asymptotic energy), μ is the reduced mass of the system, $\mathbf{V}=2\mu \mathbf{U}$ is the interaction potential matrix between channels and ${\mathbf{l}}^2$ is the matrix of orbital angular momentum. Scattering observables are obtained in the asymptotic region where the Log-Derivative matrix has a known form in terms of free-particle solutions and unknown mixing coefficients. At the end of the propagation, the Log-Derivative matrix can be used to obtain the K-matrix by solving the following linear system: (6) $({\mathbf{N}}^{\prime }-\mathbf{Y}\mathbf{N})={\mathbf{J}}^{\prime }-\mathbf{Y}\mathbf{J}$(6) where $\mathbf{J}(R)$ and $\mathbf{N}(R)$ are matrices of Riccati-Bessel and Riccati-Neumann functions [57]. From the K-matrix the S-matrix is easily obtained and from it the state-to-state scattering cross-sections. The rotational state-changing cross-sections are then obtained as (7) ${\sigma }_{j\to j^{\prime }}=\frac{\pi }{(2j+1)k_j^2}\sum _J(2J+1)\sum _{l,l^{\prime }}|{\delta }_{lj,l^{\prime }{j}^{\prime }}-S_{lj,l^{\prime }{j}^{″}}^J{|}^2.$(7) For doublet-state scattering, the above CC equations are modified by also coupling the projection of the spin angular momentum S with projection Σ on the internuclear axis [59]. The rotational basis functions in Equation (4(4) ${\mathrm{\Psi }}^{JM}(R,\mathrm{\Theta })=\frac{1}{R}\sum _{j,l}{f}_{lj}^J(R){\mathcal{Y}}_{jl}^{JM}(\hat{\mathbf{R}},\hat{\mathbf{r}})$(4) ) are changed to explicitly include the spin term. The main result of this is to modify the analytical solutions of the potential matrix elements in Equation (5(5) $(\frac{{\mathrm{d}}^2}{\mathrm{d}{R}^2}+{\mathbf{K}}^2-\mathbf{V}-\frac{{\mathbf{l}}^2}{R^2}){\mathbf{f}}^J=0.$(5) ) such that the Wigner 3-j symbols explicitly account for the electronic spin. The working equations for doublet-state scattering are given in the ASPIN publication [57] while a detailed derivation and discussion of the procedure implemented in ASPIN was given by Corey and McCourt [60]. The explicit treatment of collisions accounting for the doublet nature of the C${}_2^{-}$ molecule gives rise to spin-flip transitions in which the j quantum number changes but N is conserved.

To converge the CC equations, a rotational basis set was used which included states with up to j = 20.5 within the expansion in Equation (4(4) ${\mathrm{\Psi }}^{JM}(R,\mathrm{\Theta })=\frac{1}{R}\sum _{j,l}{f}_{lj}^J(R){\mathcal{Y}}_{jl}^{JM}(\hat{\mathbf{R}},\hat{\mathbf{r}})$(4) ). The CC equations were propagated between 1.7 and 100.0 Å in 2000 steps using the log-derivative propagator [61] up to 60 Å and the variable-phase method [62] at larger distances up to 100 Å. The convergence of the scattering calculations with respect to rotational basis set, number of terms in PES expansion, propagation distance and number of steps was checked. The cross-sections are converged to at least a few percent or better which will have a negligible effect on calculated rates, particularly compared with the 2D-PES approximation which is the largest source of approximations in the dynamics. The potential energy was interpolated between calculated $V_{\lambda }(r_{\mathrm{eq}}|R)$ values using a cubic spline and extrapolated below and above the ab initio grid using linear and polynomial functions respectively as implemented in ASPIN [57]. As our ab initio grid goes out to 25 Å and the scattering energies of interest are not in the ultracold or high energy regimes, the details of the potential extrapolation have a negligible effect on the scattering cross-sections.

Scattering calculations were carried out for the C${}_2^{-}$/p-H${}_2$(j = 0) system for collision energies between 1 and 1000 cm${}^{-1}$ using steps of 0.1 cm${}^{-1}$ for energies up to 100 cm${}^{-1}$, 0.2 cm${}^{-1}$ for 100–200 cm${}^{-1}$, 0.5 cm${}^{-1}$ for 200–300 cm${}^{-1}$, 1 cm${}^{-1}$ for 300–500 cm${}^{-1}$ and 2 cm${}^{-1}$ for 500–1000 cm${}^{-1}$. This fine energy grid was used to ensure that important features such as resonances appearing in the cross-sections were accurately accounted for (with respect to the PES used) and their contributions correctly included when the corresponding rates were calculated. Although the system has a relatively small reduced mass of 1.85948 amu, the attractive PES nevertheless required quite a large number of partial waves to be included in the scattering calculations with the number used increased with increasing energy up to J = 160. Rotationally inelastic cross-sections were computed for all transitions between j = 0.5 to j = 8.5 which should be sufficient to model buffer gas dynamics in a cold trap up to about 100 K. Only even N states are required in the calculations, due to the nuclear statistics of the ${}^{12}$C${}_2^{-}$ molecule with zero spin nuclei.

4. Rotationally inelastic scattering cross-sections & rate constants

Rotationally inelastic scattering cross-sections for C${}_2^{-}$ colliding with p-H${}_2$(j = 0) are presented in Figure 5 for various examples of both excitation ($j\to j^{\prime }$, $j^{\prime }>j$) and quenching ($j\to j^{\prime }$, $j^{\prime }<j$) processes. The profile of the scattering cross-sections is typical for such processes. For excitation processes, as channels open there is a rapid increase in the cross-section and then a gradual decrease as the collision energy increases. For quenching processes, the cross-sections are very large at low collision energies and then decrease as the energy increases. As anticipated from the Legendre expansion of the 2D PES in Equation (2(2) $V_{av}(R,\theta )=\sum _{\lambda }^{{\lambda }_{max}}{V}_{\lambda }(R)P_{\lambda }(\cos \theta )$(2) ), $\mathrm{\Delta }j=\pm 2$ cross-sections are the largest due to the marked strength of the $V_2$ coupling terms during propagation dynamics, as clearly also shown in Figure 4. Larger changes in j have smaller cross-sections on account of the larger energy differences and the smaller strengths of the $V_{\lambda }$ expansion coupling terms which directly drive those transitions.

Figure 5. Rotationally inelastic scattering cross-sections for C${}_2^{-}$ colliding with p-H${}_2$($j= 0$) (solid lines) and He (dashed lines) for excitation (top panels) and quenching (bottom panels).

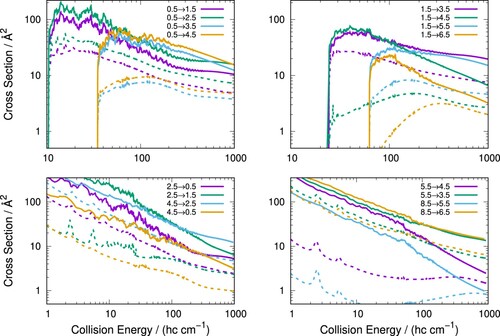
Figure 5 also shows details specific to scattering involving a doublet species. For all examples shown, cross-sections for $\mathrm{\Delta }N$ transitions which conserve spin are favoured (e.g. $j=8.5\to j^{\prime }=6.5$) as is expected [59] although for some examples the spin-conserving and spin-flip transitions are very similar (e.g. $j=1.5\to j^{\prime }=3.5/4.5$). Also shown in Figure 5 is an example of an N conserving spin-flip for $j=2.5\to j=1.5$. This process is either slightly endo- or exo-ergic depending on the considered j state but can also be considered as an essentially elastic process for the purposes of buffer gas cooling dynamics which we shall discuss below.

At lower collision energies up to around 100 cm${}^{-1}$ the cross-sections have a rich structure with many resonances (also see Figure 6). While not the focus of this work, such features are caused by either shape resonances, related to trapping of incoming particles behind centrifugal barriers for specific partial waves, or Feshbach resonances, caused by virtual excitation of the target molecule to low-lying rotational levels.

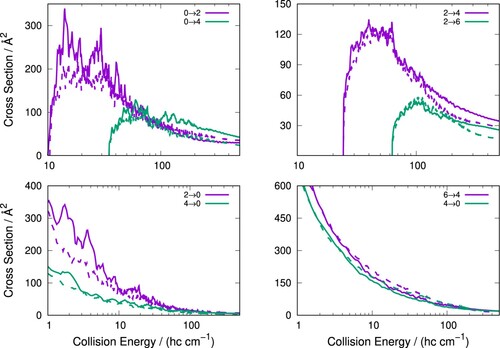
Figure 6. Rotationally inelastic scattering cross-sections for pseudo-singlet C${}_2^{-}$ colliding with para-H${}_2$(j = 0) (solid lines) and with Ar (dashed lines) for excitation (top panels) and quenching (bottom panels).

The scattering cross-sections for the corresponding transitions for C${}_2^{-}$/He collisions, which we have previously calculated [31], are also shown in Figure 5 allowing comparisons to be made with those for C${}_2^{-}$/p-H${}_2$(j = 0) system. Cross-sections for C${}_2^{-}$ colliding with molecular hydrogen turn out to be significantly larger than those for He, as anticipated in the previous discussion and clearly due to the stronger interaction in the former system compared with the latter.

A further comparison of the excitation and quenching cross-sections is provided in Figure 6 which present the rotationally inelastic cross-sections for C${}_2^{-}$ colliding with both p-H${}_2$(j = 0) and Ar. For the C${}_2^{-}$/Ar system, the anion was treated as a pseudo-singlet (${}^1\mathrm{\Sigma }$) as the rate constants for the collisional cooling process were of primary interest [32]. This constraint simplifies the dynamics but does not greatly affect the accuracy of the calculations, as discussed previously in our earlier studies [31,63]. To compare the C${}_2^{-}$/p-H${}_2$(j = 0) cross-sections to those of pseudo-singlet C${}_2^{-}$/Ar, the relevant summed doublet cross-sections are used which are obtained by simply adding both cross-sections for the same final N state but different j state, for example ${\sigma }_{0.5\to 2.5}+{\sigma }_{0.5\to 1.5}$ is compared to ${\sigma }_{0\to 2}$ for the pseudo-singlet case.

From Figure 6, it can be seen that the C${}_2^{-}$/p-H${}_2$(j = 0) and C${}_2^{-}$/Ar cross-sections are relatively similar with the profiles of the scattering cross-sections over the examined energy range significantly overlapping. For all transitions shown, the scattering cross-sections are always larger for the C${}_2^{-}$/p.H${}_2$(j = 0) system. This is a consequence of both the greater strength of the $V_2$ coupling term (and with a deeper attractive well) for the H${}_2$ collision partner than for Ar (Figure 4). The next higher coupling term $V_4$ is also more repulsive for the former partner than with the latter noble gas.

The rotationally inelastic rate constants $k_{j\to j^{\prime }}(T)$ can be evaluated next as the convolution of the previous scattering cross-sections over a Boltzmann distribution of the relative collision energies: (8) $k_{j\to j^{\prime }}(T)={\left(\frac{8}{\pi \mu k_b^3{T}^3}\right)}^{1/2}{\int }_0^{\mathrm{\infty }}{E}_c{\sigma }_{j\to j^{\prime }}(E_c)e^{-E_c/k_{B}T}\mathrm{d}{E}_c.$(8) where $E_c=\mu v^2/2$ is the kinetic energy in the collision calculations. Rate constants were obtained for all transitions between j = 0.5 and j = 8.5.

The rate constants for C${}_2^{-}$/p-H${}_2$(j = 0) calculated here and those for C${}_2^{-}$/He which we have previously obtained in our earlier work [31] can be used now to check an approximation which is often employed in astrophysical modelling studies ( e.g. see: [64]), consisting in using the collisionally inelastic coefficients computed for the helium partner to further obtain those for H${}_2$ as a partner by assuming the same value of their scattering cross-sections. The rate coefficients are then obtained using a scaling factor given by the ratio of the reduced masses as (9) $f1=\frac{k_{{\mathrm{H}}_2}}{k_{\mathrm{He}}}=\sqrt{\frac{{\mu }_{{\mathrm{C}}_2^{-}/\mathrm{He}}}{{\mu }_{{\mathrm{C}}_2^{-}/{\mathrm{H}}_2}}}=\mathrm{1.37.}$(9) For scaling collisions of He and H${}_2$ with molecular ions, a slightly more sophisticated scale factor can be used to additionally account for the differences between the ionic interactions: (10) $f2=\frac{k_{{\mathrm{H}}_2}}{k_{\mathrm{He}}}=\sqrt{\frac{{\alpha }^{st}({\mathrm{H}}_2)/{\mu }_{{\mathrm{C}}_2^{-}/{\mathrm{H}}_2}}{{\alpha }^{st}(\mathrm{He})/{\mu }_{{\mathrm{C}}_2^{-}/\mathrm{He}}}}=2.7$(10) where ${\alpha }^{st}(\mathrm{He})=1.384$ $a_0^3$ and ${\alpha }^{st}({\mathrm{H}}_2)=5.314$ $a_0^3$ are the polarisabilities of He and H${}_2$, respectively.

The procedure has been shown to be reasonable for some neutral systems, for example, for SiS Lique et al. found rotationally inelastic rate constants for H${}_2$ and those for He scaled by $f1$ were within a maximum error of a factor of two [52]. In contrast, for CO [64] and CN [65], the approximation was found to be unreliable.

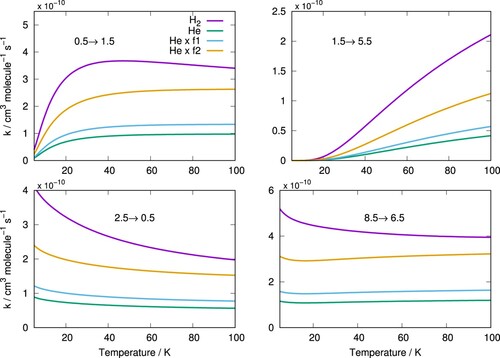
The rate constants for C${}_2^{-}$/p-H${}_2$(j = 0) and for C${}_2^{-}$/He along with the latter multiplied by the scaling factors $f1$ and $f2$ for four example transitions are shown in Figure 7. The rate constants for C${}_2^{-}$/p-H${}_2$(j = 0) are about four times larger than those for C${}_2^{-}$/He and thus neither scaling factor is sufficiently realistic to obtain from it data within a reasonably approximation. This is not surprising as the simple factor $f1$ has already been shown to be unreliable for ion targets before [54,66] due to the difference in the polarisabilities of He and H${}_2$ which results in different long range interactions. However, even accounting for this long-range effect by further using the $f2$ factor is not enough to provide reliable scaled results for the case of the C${}_2^{-}$ anion, as we had also demonstrated for the similar CN${}^{-}$ anion [67]. It is thus proven once again that for He and H${}_2$, two of the most important species in astronomical environments, explicit treatment of actual quantum dynamics for both species is essential for finally obtaining accurate rate constant values to be used in any further chemical networks modelling.

Figure 7. Examples of rotationally inelastic rate constants $k_{j\to j^{\prime }}(T)$ for for C${}_2^{-}$ colliding with H${}_2$ and He. Rate constants obtained by multiplying those of He by $f1$ and $f2$ factors are also shown.

The rate constants for the rotationally inelastic transitions corresponding to those of Figure 6 for temperatures between 5 and 100 K are shown in Figure 8, comparing those for C${}_2^{-}$/p-H${}_2$(j = 0) and C${}_2^{-}$/Ar. These are given for N states and are obtained in a similar manner to when we obtained the pseudo-singlet cross-sections, i.e. by summing all the relevant rate constant components at each temperature.

Figure 8. Rotationally inelastic rate constants $k_{N\to N^{\prime }}(T)$ for corresponding transitions of Figure 6 for C${}_2^{-}$ colliding with p-H${}_2$(j = 0) (solid lines) and Ar (dashed lines).

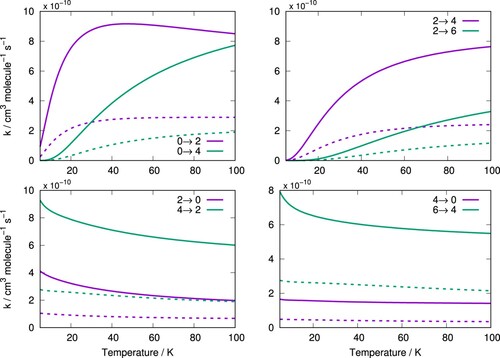
Following the behaviour, we have already noticed for the scattering cross-sections, the rate constants for the $\mathrm{\Delta }N=2$ transitions are now the largest. The rate constants for collisions with p-H${}_2$(j = 0) are about three or four times larger than those for Ar for corresponding transitions. This is also a consequence of the reduced mass μ effect as this quantity appears in the denominator of Equation (8(8) $k_{j\to j^{\prime }}(T)={\left(\frac{8}{\pi \mu k_b^3{T}^3}\right)}^{1/2}{\int }_0^{\mathrm{\infty }}{E}_c{\sigma }_{j\to j^{\prime }}(E_c)e^{-E_c/k_{B}T}\mathrm{d}{E}_c.$(8) ). The ratio of both systems reduced mass is $({\mu }_{{\mathrm{C}}_2^{-}/\mathrm{Ar}}/{\mu }_{{\mathrm{C}}_2^{-}/{\mathrm{H}}_2}{)}^{1/2}\approx (\frac{15}{1.86}{)}^{1/2}=2.8$ and therefore, if the scattering cross-sections were exactly equal, the rates for C${}_2^{-}$/p-H${}_2$(j = 0) would be around three times larger than those for C${}_2^{-}$/Ar. The even greater difference is therefore due to the additional role in the dynamics of the differences between the relative strengths of the coupling multipolar coefficients of the two systems, as discussed earlier. The larger rate constants which we have found here for collisions with the molecular hydrogen will therefore lead to even faster thermalisation times than those we had found for the case of Ar, as will be demonstrated by the results presented in the next section.

The results obtained here can also be usefully compared to those yielded by similar systems. For example, the cross-sections and rate coefficients for rotationally inelastic transitions in the case of C${}_2^{-}$ colliding with Li and Rb were found to be quite similar to each other [26] and far larger (between 4 and 10 times) than those reported here for the p-H${}_2$(j=0) partner, as a consequence of the much stronger interactions shown by the former partners as we had mentioned earlier in this paper. The CN${}^{-}$ anion can also be considered for comparison since we had found that its rotationally inelastic collisions with p-H${}_2$(j = 0) and with Ar yield cross-sections and rate coefficients which are more similar with each other than what we have found with C${}_2^{-}$, particularly for the low $\mathrm{\Delta }N$ transitions [34].

It is also of interest at this point to define a further indicator of energy-transfer efficiency, which can be defined as a quenching function, $Q_N(T)$, which for each of the systems that we shall consider combines at a given value of N the rates of de-excitation to all lower energy states allowed by selection rules: (11) $Q_N(T)=\sum _{j,N^{\prime },j^{\prime }}{k}_{N_j\to N_{j^{\prime }}^{\prime }}(T)$(11)

To make its effect to be seen more directly in quantitative terms, we compare the results of the quenching functions above for two different collision partners of the title anion: the He atom and the p-H${}_2$(j = 0) molecule. In the examples given by Figure 9 the quenching functions obtained for both p-H${}_2$(j = 0) and He as buffer gases with the molecular anion are calculated starting from two different rotational states, which are populated in the trap range of temperatures, and at different initial temperatures.

Figure 9. Computed quenching functions for C${}_2^{-}$ interacting with p-H${}_2$(j = 0) (solid lines) and He (dashed lines) as function of the expected range of trap temperatures. Two different initial rotational states are shown as examples for both systems. See main text for further comments.

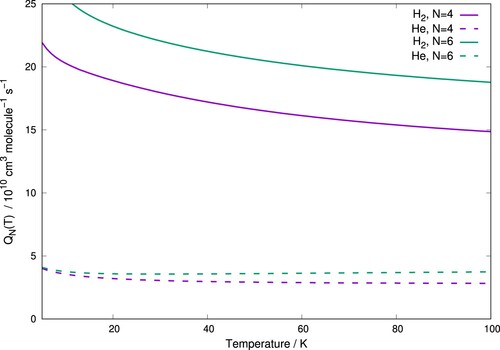
The data in that Figure clearly show the larger rotational cooling efficiency exhibited by having the hydrogen molecule as a buffer partner to the present molecular anion as opposed to the more usual He atomic gas. The values of the computed $Q_N(T)$ for the former partner are uniformly a factor of four-to-five larger than in the case of the latter gas. The actual consequences when modelling the kinetics of the thermalisation processes will be more specifically discussed in the next Section.

The rate constants for C${}_2^{-}$/p-H${}_2$(j = 0) for all transitions between j = 0.5 and j = 8.5 from 5–100 K in 1 K intervals are given in the supplementary information.

5. Kinetic modelling of thermalisation time in cold ion traps

The rate constants for rotationally inelastic collisions presented in Section 4 can be used to model the thermalisation kinetics of C${}_2^{-}$ molecules in an ion trap, using p-H${}_2$(j = 0) as the only component as a buffer gas so that we can focus on the collisional de-excitation of the molecular anion only as the dominant process. The evolution of the C${}_2^{-}$ anion's rotational state populations $n_i(t)$ induced by collisions are modelled by solving the following rate equations (12) $\frac{\mathrm{d}{n}_i(t)}{\mathrm{d}t}=\sum _{j\ne i}{n}_j(t)C_{ji}(T)-n_i(t)\sum _{i\ne j}{P}_{ij}(T).$(12) $P_{ij}(T)$ are the rates for the destruction of the population of level i, while its formation rates are given by the $C_{ji}(T)$ coefficients. The coefficients are given as a function of the inelastic rate coefficients and the gas density η as (13) $\begin{array}{rl}{P}_{ij}(T)& =\eta k_{i\to j}(T)\end{array}$(13) (14) $\begin{array}{rl}{C}_{ji}(T)& =\eta k_{j\to i}(T).\end{array}$(14) The initial rotational populations and the collisional temperature T of the trap are parameters to be selected. Equations (12(12) $\frac{\mathrm{d}{n}_i(t)}{\mathrm{d}t}=\sum _{j\ne i}{n}_j(t)C_{ji}(T)-n_i(t)\sum _{i\ne j}{P}_{ij}(T).$(12) ) were solved using the fourth order Runge-Kutta method. The rates due to spontaneous radiative processes are usually negligible in such simulations due to the high buffer gas pressure resulting in collisional rates being the dominant process in changing the molecule's rotational state [68]. For C${}_2^{-}$, this is an even better approximation since the anion has no dipole moment and thus dipole transitions are forbidden. The populations of the rotational states approach their steady-state values after a time interval, a consequence of the principle of detailed balance. As mentioned earlier, only the populations of the rotational N states will be considered here.

In the current trap experiments involving ${}^{12}$C${}_2^{-}$, the density of the anion is assumed to typically be of the order of 10${}^3$/cm${}^3$. Hence, ion-ion collisions are not relevant at those conditions and temperatures.

Figure 10 shows the simulation of C${}_2^{-}$ thermalisation using He, Ar and H${}_2$ as buffer gases at 20 K. The initial rotational populations $n_i(t=0)$ of the anion are set to those of a Boltzmann distribution at 100 K and the buffer gas density η is chosen as ${10}^{10}$ cm${}^{-3}$ or ${10}^9$ cm${}^{-3}$, typical for ion traps [69].

Figure 10. Thermalisation of C${}_2^{-}$ rotational N states during collisions with He, Ar and H${}_2$ at 20 K. Initial populations are taken from a Boltzmann distribution at 100 K. Gas pressure η is set as ${10}^{10}$ cm${}^{-3}$ except for the ‘low P’ plot where ${10}^9$ cm${}^{-3}$ was used. Vertical dashed line indicates when populations reach steady-state value as defined in the main text.

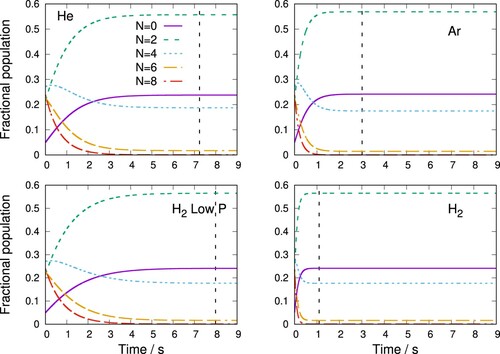
Below 50 K the vapour pressure of argon decreases sharply so that argon buffer gas can only be employed in experiments above this temperature [70]. The 20  K temperature for the simulation in Figure 10 is, therefore, feasible for He and H${}_2$ but not Ar and the latter is included for comparison purposes.

In Figure 10, the vertical dashed line is used to indicate the time when the rotational states reach thermal equilibrium which was defined to be when the N = 0 state's population $n_0$ remains unchanged in the forth decimal place. This definition is the same as that chosen in our previous work on CN${}^{-}$/He/Ar/H${}_2$ collisions [34] and allows comparisons between these systems.

From the data shown in that Figure it can be seen that using the hydrogen molecule as a buffer gas leads to the fastest thermalisation time, with the C${}_2^{-}$ rotational populations reaching steady-state values in around only 1 s. This compares to 3 s for Ar and just over 7 s for He. This is a consequence of the larger rotationally inelastic rate coefficients for C${}_2^{-}$/p-H${}_2$(j = 0) scattering computed and discussed in the previous Section, which is in turn linked, as described above, to the varying strengths of the interactions between these species. To further underline how efficient H${}_2$ is as a buffer gas, we report in Figure 10 a low pressure simulation where the gas density η of H${}_2$ was set an order of magnitude lower, at ${10}^9$ cm${}^{-3}$, in comparison with the two noble gases. In this case, we find the thermalisation time to be of about 8 s, which is still similar to that shown there for He with $\eta ={10}^{10}$ cm${}^{-3}$.

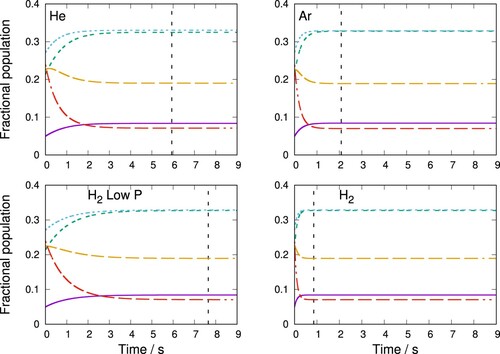
Figure 11 shows a similar simulation but for a gas temperatures of 60 K. At this higher temperature, the thermalisation times are slightly shorter as the populations are closer to their initial values at 100 K. The results are similar to those at 20 K with H${}_2$ providing the fastest thermalisation time of just under 1 second while for Ar, around 2 s are required. Again the low-pressure H${}_2$ simulation shows thermalisation times which are somewhat comparable to those given when using He at the higher gas pressure indicated in the Figure.

Figure 11. Thermalisation of C${}_2^{-}$ rotational states during collisions with He, Ar and p-H${}_2$(j = 0) (right panel) at 60 K Other parameters are the same as those of Figure 10.

It is also of interest to compare the results presented here for the C${}_2^{-}$ thermalisation process in the traps to those obtained for the CN${}^{-}$ anion, for which we have already carried out similar simulations in our earlier work [34]. The trends shown by those results turn out to be essentially the same, with the thermalisation times induced on the latter molecular anion by the p-H${}_2$(j = 0) partner gas being about twice as fast as those due to Ar and He, with He again turning out to be the slowest. To give a more specific comparison, at 60 K the thermalisation times for CN${}^{-}$ were 1, 2 and 3 s for p.H${}_2$(j = 0), Ar and He, respectively. An important difference in the case of the CN${}^{-}$ rotor is that $\mathrm{\Delta }N=1$ transitions are also allowed, therefore different state-changing kinetics and energy gaps are possible than for C${}_2^{-}$. Nevertheless, these molecular anions have shown from our calculations to exhibit similar rotational thermalisation times when the same buffer gases are used in the kinetics simulations.

6. Quadrupole transitions & critical densities

As the C${}_2^{-}$ molecule is a homonuclear diatomic, it has no permanent electric dipole moment and thus spontaneous emission of light via dipole transitions are forbidden. Instead, the molecule can lose energy via slower quadrupole transitions. Following the derivation presented a while ago by Wolniewicz, Simbotin and Dalgarno [71] the probability for these transitions to occur from an initial state ${\nu }^{\prime },N^{\prime }$ to a final state ${\nu }^{″},N^{″}$ is given as (15) $\begin{array}{rl}& A({\nu }^{\prime }{N}^{\prime },{\nu }^{″}{N}^{″})\\ & =1.4258\times {10}^4(E_{{\nu }^{\prime }{N}^{\prime }}-E_{{\nu }^{″}{N}^{″}}{)}^5\\ & \times |⟨{\chi }_{{\nu }^{\prime }{N}^{\prime }}|Q(R)|{\chi }_{{\nu }^{″}{N}^{″}}⟩|f(N^{\prime },N^{″}){\mathrm{s}}^{-1}.\end{array}$(15) where the numerical factor on the r.h.s. converts atomic units to s${}^{-1}$. For the rigid rotor approximation applied here, the integral over the radial coordinate can be taken as a constant, thereby giving (16) $\begin{array}{rl}& A(N^{\prime },N^{″})\\ & =1.4258\times {10}^4(E_{N^{\prime }}-E_{N^{″}}{)}^{5}Q(r_e)f(N^{\prime },N^{″}){\mathrm{s}}^{-1}.\end{array}$(16) The angular coefficient $f(N^{\prime },N^{″})$ for the $N^{″}=N^{\prime }-2$ transitions of interest here is given as (17) $f(N^{\prime },N^{″})=\frac{3N^{\prime }(N^{\prime }-1)}{2(2N^{\prime }-1)(2N^{\prime }+1)}.$(17) The quadrupole moments of C${}_2^{-}$ were calculated for $r_e$, using MOLPRO, to have values of ${\mathrm{\Theta }}_{xx}$ = ${\mathrm{\Theta }}_{yy}$ = 0.69043 and ${\mathrm{\Theta }}_{zz}$ = 1.38086 in atomic units. For linear molecules such as C${}_2^{-}$, the relationship ${\mathrm{\Theta }}_{zz}=-2{\mathrm{\Theta }}_{xx}=-2{\mathrm{\Theta }}_{yy}$ holds [72]. It is the ${\mathrm{\Theta }}_{zz}$ component which is measured experimentally [73] and this is taken as $Q(r_e)$ in Equation (16(16) $\begin{array}{rl}& A(N^{\prime },N^{″})\\ & =1.4258\times {10}^4(E_{N^{\prime }}-E_{N^{″}}{)}^{5}Q(r_e)f(N^{\prime },N^{″}){\mathrm{s}}^{-1}.\end{array}$(16) ).

The quadrupole transition probabilities for C${}_2^{-}$ computed using Equation (16(16) $\begin{array}{rl}& A(N^{\prime },N^{″})\\ & =1.4258\times {10}^4(E_{N^{\prime }}-E_{N^{″}}{)}^{5}Q(r_e)f(N^{\prime },N^{″}){\mathrm{s}}^{-1}.\end{array}$(16) ) and neglecting the fine splitting, are presented in Table 1 and compared those for para-H${}_2$. The probabilities for C${}_2^{-}$ are found to be extremely small due to the dependence of the transition probability on a large power in the $(\mathrm{\Delta }E{)}^5$ term. The rotational constant for H${}_2$ is around 60 cm${}^{-1}$, to be compared to 1.7438 cm${}^{-1}$ for C${}_2^{-}$. This much smaller energy spacing for the anion, further raised to the fifth power in Equation (16(16) $\begin{array}{rl}& A(N^{\prime },N^{″})\\ & =1.4258\times {10}^4(E_{N^{\prime }}-E_{N^{″}}{)}^{5}Q(r_e)f(N^{\prime },N^{″}){\mathrm{s}}^{-1}.\end{array}$(16) ), accounts for the orders of magnitude differences between the computed lifetimes for C${}_2^{-}$ and for para-H${}_2$.

Table 1. Quadrupole transitions probabilities for $\mathrm{\Delta }N=-2$ transitions for C${}_2^{-}$ and para-H${}_2$ [71]. Units of s${}^{-1}$.

Transition	C${}_2^{-}$	H${}_2$
$2\to 0$	$9.7\times {10}^{-19}$	$2.9\times {10}^{-11}$
$4\to 2$	$9.6\times {10}^{-18}$	$2.8\times {10}^{-9}$
$6\to 4$	$1.0\times {10}^{-15}$	$2.6\times {10}^{-8}$
$8\to 6$	$5.0\times {10}^{-15}$	$1.1\times {10}^{-7}$

To assess the gas density values required so that the rates for collisional state-changing processes can match in size those with the competing emission via spontaneous decay, the concept of a critical density is often used in the astrophysical literature [67,74]. The latter quantity is defined as (18) $n_{\mathrm{crit}}^i(T)=\frac{A_{ij}}{\sum _{j\ne i}{k}_{ij}(T)}$(18) where $A_{ij}$ is the Einstein A coefficient for spontaneous dipole emission. Critical densities are is used in astronomical contexts to asses the possible densities required for local thermal equilibrium (LTE) to be reached and are usually applied for rotational transitions in molecules that can occur in the interstellar medium (ISM) or which have been observed there already.

Since in C${}_2^{-}$, dipole emission is forbidden, the anion can only lose energy spontaneously via the far slower quadrupole emission process. The transition probabilities given for C${}_2^{-}$ in Table 1 are found to be so small in comparison to the rotationally inelastic collisional rate coefficients, for both para-H${}_2$(j = 0) and He, that critical densities easily reach the values which are expected to exist for the estimated conditions in several molecular clouds. For example, when inserting the values for quadrupole emission from Table 1 into Equation (18(18) $n_{\mathrm{crit}}^i(T)=\frac{A_{ij}}{\sum _{j\ne i}{k}_{ij}(T)}$(18) ), and further using the rate coefficients for para-H${}_2$(j = 0) obtained in the present work, we obtain that the $n_{\mathrm{crit}}^i$ values are around ${10}^{-6}$ cm${}^{-3}$. On the other hand, the expected molecular densities of diffuse molecular clouds are estimated to be around 10${}^2$ cm${}^{-3}$, whereas dense molecular clouds are considered to be between 10${}^3$ – 10${}^6$ cm${}^{-3}$ [75,76]. This means that the rotational levels of C${}_2^{-}$, if this specific anion would be found to be present in the interstellar medium, should be under much higher densities and therefore be able collisionally reach for its rotational state populations a Local Thermal Equilibrium( LTE) situation. For observational purposes, the latter should be a useful piece of information when searching within the rotational substructure of the traditional electronic band employed in astronomical observations of the title anion [43].

7. Conclusions

We have calculated rotationally inelastic cross-sections and corresponding rate coefficients for the case of C${}_2^{-}$ colliding with molecular hydrogen, using a new ab initio PES which describes their interaction for the case of the para-H${}_2$(j = 0). The quantum scattering calculations were simplified by averaging over the H${}_2$ orientations to obtain a 2D-PES for that specific situation. The cross-sections for C${}_2^{-}$/p-H${}_2$(j = 0) and C${}_2^{-}$/Ar collisions were found to be similar leading to larger rate coefficients for the molecular hydrogen partner on account of the much smaller mass of this specific system. This in turn gave shorter thermalisation times, thereby showing that para-H${}_2$(j = 0) is an efficient buffer gas partner for cooling C${}_2^{-}$. We have further compared the rate coefficients for the C${}_2^{-}$/p-H${}_2$(j = 0) ensemble with those of C${}_2^{-}$/He, where the present results showed that scaling factors are not sufficient to allow the former system to be realistically approximated by scaling the latter with a fixed numerical prescription as discussed by us in the previous sections.

As C${}_2^{-}$ has no permanent dipole, spontaneous transitions can only occur through very slow quadrupole transitions, for which we have calculated here the corresponding Einstein coefficients for spontaneous emissions between rotational states. Combining these radiative emission findings with the collisional inelastic rate coefficients computed in this study, allows us to suggest that, in case the C${}_2^{-}$ anion would be present in the ISM and in exo-planetary atmospheres, then it should be in a rotational LTE within the various ISM environments discussed in the previous Section. This result should be useful for planning possible new observations of the rotational substructure of the Herzberg-Lagerqvist spectrum associated with the $B^2{\mathrm{\Sigma }}_u^{+}$–$X^2{\mathrm{\Sigma }}_g^{+}$ electronic band employed in astronomical searches of the present molecular ion [43].

The calculations we have presented here could naturally be further extended to check the quality of the reduced-dimensionality, 2D approximation we have used in the present study. This would include completing the grid calculations we have done so far to attain a denser 4D PES and then carrying out the scattering calculations treating C${}_2^{-}$ and H${}_2$ as rigid rotors. This would also allow a comparison of para- and ortho-H${}_2$ partners in collisions with C${}_2^{-}$. However, the fairly large rotationally inelastic rate coefficients obtained here for the C${}_2^{-}$/p.H${}_2$(j = 0) system collisions, and the clearly efficient thermalisation modelling we have presented, suggest that it is worth considering molecular hydrogen as a possible buffer gas to also quench the internal vibrational motion of C${}_2^{-}$, a result providing an important prerequisite for subsequent laser cooling experiments and simulations. We have already shown, in fact, that for the case of Ar as a buffer gas partner, the vibrational quenching rate constants for $\nu =2$ and $\nu =1$ are of reasonable magnitude [33]to be of interest in cold ion trap studies. However, and as discussed earlier in the present study, Ar can only be used down to around 50 K, which would be a significant limitation for cold ion studies. In contrast, because of its low reactivity with C${}_2^{-}$ and because it remains gaseous down to a few Kelvin, molecular hydrogen could be a more suitable buffer gas to further be employed for vibrational quenching of C${}_2^{-}$. This will be the subject of another study currently in preparation in our group.

Acknowledgments

The authors acknowledge computer resources made available by the computer centre WCSS (Wroclawskie Centrum Sieciowo-Superkomputerowe, Politechnika Wroclawska). The computational results presented here have also been achieved (in part) using the LEO HPC infrastructure of the University of Innsbruck. F. A. G. and R. W. suggested the project. F. A. G. followed and guided the development of the calculations. J. F. carried out the quantum structure calculations and B. M. carried out the quantum scattering and kinetics calculations. All authors have contributed to the analysis and presentation of the results and to the discussion of the conclusions reached in this work.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Correction Statement

This article has been corrected with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

F. A. G. and R. W. acknowledge financial support by the Austrian Science Fund (FWF) through Project No. P29558-N36. J. F. acknowledges the WCSS (Poland) funding support via grant n. KDM-408.